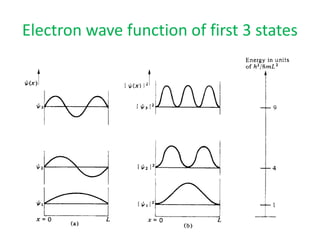
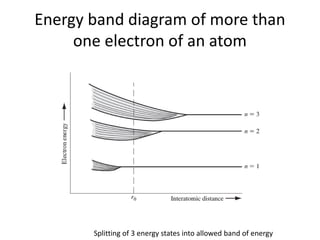
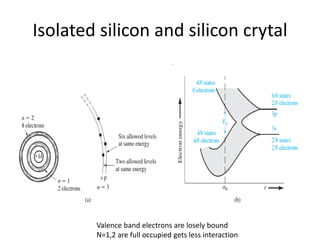
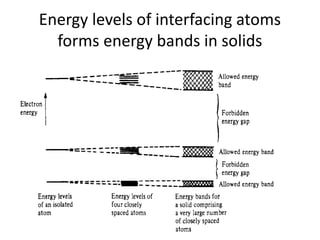
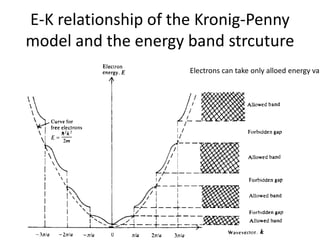
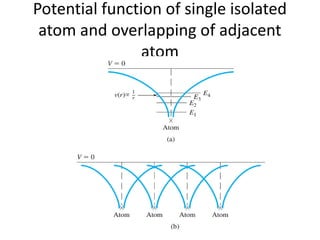
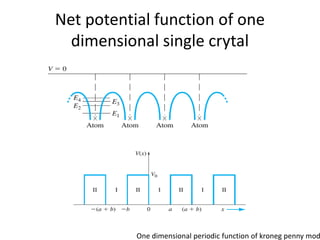
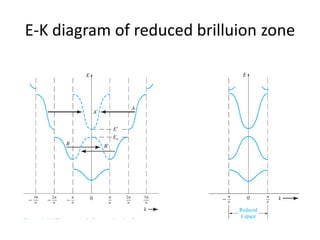
This document provides a summary of quantum mechanical concepts and solid state physics. It begins with a review of quantum mechanics and the Schrodinger equation. It then discusses the wave nature of electrons and how the Schrodinger equation describes the wavefunction and probability of finding an electron. It also covers energy band diagrams and how the periodic potential in solids leads to the formation of allowed energy bands. It discusses these concepts for isolated atoms, silicon crystals, and the one-dimensional Kronig-Penny model.

1. • Review of quantum mechanical concept
• Review of solid state physics
Unit-I
Prepared by
S.Vijayakumar, AP/ECE
Ramco Institute of Technology
Academic year
(2017-2018 odd sem)

2. • “I think that I can safely say that nobody
understands quantum mechanics.”—
Richard Feynman (Nobel Prize, 1965)

3. Erwin Rudolf Josef Alexander Schrödinger
Born: 12 Aug 1887 in Erdberg, Vienna, Austria
Died: 4 Jan 1961 in Vienna, Austria
Nobel Prize in Physics 1933
"for the discovery of new productive forms of atomic theory"

4. An equation for matter waves?
De Broglie postulated that every particles has an associated wave of wavelength:
ph/=λ
Wave nature of matter confirmed by electron diffraction studies etc (see earlier).
If matter has wave-like properties then there must be a mathematical function that is the
solution to a differential equation that describes electrons, atoms and molecules.
The differential equation is called the Schrödinger equation and its solution is called the
wavefunction, Ψ.
What is the form of the Schrödinger equation ?

5. Electron wave function of first 3 states

6. Interpretation of Ψ(x,t)
As mentioned previously the TDSE has solutions that are inherently complex ⇒Ψ (x,t)
cannot be a physical wave (e.g. electromagnetic waves). Therefore how can Ψ (x,t)
relate to real physical measurements on a system?
The Born Interpretation
dxtxPdxtxdxtxtx ),(),(),(),(
2*
=Ψ=ΨΨ
Ψ*Ψ is real as required for a probability distribution and is the probability per unit
length (or volume in 3d).
The Born interpretation therefore calls Ψ the probability amplitude, Ψ*Ψ (= P(x,t) )
the probability density and Ψ*Ψ dx the probability.
Probability of finding a particle in a small length dx at position x and time t is equal to

7. Normalisation
∫∫
∞
∞−
∞
∞−
=Ψ= 1),()(
2
dxtxdxxP
Total probability of finding a particle anywhere must be 1:
This requirement is known as the Normalisation condition.

8. Energy band diagram of more than
one electron of an atom
Splitting of 3 energy states into allowed band of energy

9. Isolated silicon and silicon crytal
Valence band electrons are losely bound
N=1,2 are full occupied gets less interaction

10. Energy levels of interfacing atoms
forms energy bands in solids

11. E-K relationship of the Kronig-Penny
model and the energy band strcuture
Electrons can take only alloed energy va

12. Potential function of single isolated
atom and overlapping of adjacent
atom

13. Net potential function of one
dimensional single crytal
One dimensional periodic function of kroneg penny mod

14. E-K diagram of reduced brilluion zone