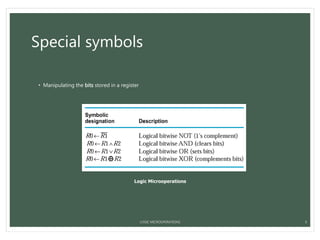
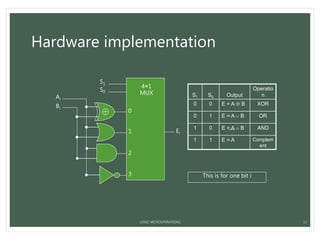
The document provides an overview of logic microoperations in computer organization and architecture, detailing special symbols, the list of operations, and hardware implementation. It explains various logic functions and their representations, such as AND, OR, XOR, and their uses for manipulating individual bits in registers. Additionally, it discusses applications like selective set, complement, clear, mask operations, and insert operations for managing data within registers.

1. BIRLA VISHWAKARMA
MAHAVIDHYALAYA
COMPUTER ORGANIZATION AND ARCHITECTURE
Presented by: Vatsal Trivedi
LOGIC MICROOPERATIONS
1

2. Index
1. Introduction
2. Special symbols
3. List of logic microoperations
4. Hardware implementation
5. Applications of logic microoperations
LOGIC MICROOPERATIONS 2

3. Introduction
LOGIC MICROOPERATIONS 3

4. Example
LOGIC MICROOPERATIONS 4

5. Special symbols
OR Microoperation
• Symbol: , +
• Gate:
• Example: 1001102  10101102 = 11101102
P+Q: R1←R2+R3, R4←R5 R6
5
OR
OR
ADD
LOGIC MICROOPERATIONS

6. Special symbols
AND Microoperation
• Symbol: 
• Gate:
• Example: 1001102  10101102 = 00001102
6LOGIC MICROOPERATIONS

7. Special symbols
Complement (NOT) Microoperation
• Symbol:

• Gate:
• Example: 10101102 = 01010012
7LOGIC MICROOPERATIONS

8. Special symbols
XOR (Exclusive-OR) Microoperation
• Symbol: 
• Gate:
• Example: 1001102  10101102 = 11100002
8LOGIC MICROOPERATIONS

9. Special symbols
• Manipulating the bits stored in a register
Logic Microoperations
LOGIC MICROOPERATIONS 9

10. List of logic microoperations
• There are, in principle, 16 different logic functions that can be defined over two binary input
variables
X Y F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
Truth Table for 16 Functions of Two Variables
LOGIC MICROOPERATIONS 10

11. Sixteen Logic Microoperations
Boolean function Microoperation Name
F0 = 0 F ← 0 Clear
F1 = xy F ← A∧B AND
F2 = xy’ F ← A∧B
F3 = x F ← A Transfer A
F4 = x’y F ← A∧B
F5 = y F ← B Transfer B
F6 = x  y F ← A B Ex-OR
F7 = x+y F ← A∨B OR
Boolean function Microoperation Name
F8 = (x+y)’ F ← A∨B NOR
F9 = (x  y)’ F ← A B Ex-NOR
F10 = y’ F ← B Compl-B
F11 = x+y’ F ← A∨B
F12 = x’ F ← A Compl-A
F13 = x’+y F ← A∨B
F14 = (xy)’ F ← A∧B NAND
F15 = 1 F ← all 1’s set to all 1’s
List of logic microoperations
- 16 different logic operations with 2
binary vars.
- n binary vars → functions2 2 n
LOGIC MICROOPERATIONS 11

12. Hardware implementation
• The hardware implementation of logic microoperations requires that logic gates be inserted for
each bit or pair of bits in the registers to perform the required logic function
• Most computers use only four (AND, OR, XOR, and NOT) from which all others can be derived.
LOGIC MICROOPERATIONS 12

13. Hardware implementation
S1 S0 Output
Operatio
n
0 0 E = A  B XOR
0 1 E = A  B OR
1 0 E = A  B AND
1 1 E = A Complem
ent
S1
S0
0
1
2
3
4×1
MUX
Ei
Ai
Bi
This is for one bit i
LOGIC MICROOPERATIONS 13

14. Applications of logic
microoperations
• Logic microoperations can be used to manipulate individual bits or a portions of a
word in a register
• Consider the data in a register A. In another register, B, is bit data that will be used to
modify the contents of A
• Selective-set A  A + B
• Selective-complement A  A  B
• Selective-clear A  A • B’
• Mask (Delete) A  A • B
• Clear A  A  B
• Insert A  (A • B) + C
• Compare A  A  B
• . . .
LOGIC MICROOPERATIONS 14

15. Selective set
• In a selective set operation, the bit pattern in B is used to set certain bits in A
1 1 0 0 At
1 0 1 0 B
1 1 1 0 At+1 (A  A + B)
• If a bit in B is set to 1, that same position in A gets set to 1, otherwise that bit in A
keeps its previous value
LOGIC MICROOPERATIONS 15

16. Selective complement
• In a selective complement operation, the bit pattern in B is used to complement
certain bits in A
1 1 0 0 At
1 0 1 0 B
0 1 1 0 At+1 (A  A  B)
• If a bit in B is set to 1, that same position in A gets complemented from its original
value, otherwise it is unchanged
LOGIC MICROOPERATIONS 16

17. Selective clear
• In a selective clear operation, the bit pattern in B is used to clear certain bits in A
1 1 0 0 At
1 0 1 0 B
0 1 0 0 At+1 (A  A  B’)
• If a bit in B is set to 1, that same position in A gets set to 0, otherwise it is unchanged
LOGIC MICROOPERATIONS 17

18. Mask operation
• In a mask operation, the bit pattern in B is used to clear certain bits in A
1 1 0 0 At
1 0 1 0 B
1 0 0 0 At+1 (A  A  B)
• If a bit in B is set to 0, that same position in A gets set to 0, otherwise it is unchanged
LOGIC MICROOPERATIONS 18

19. Clear operation
• In a clear operation, if the bits in the same position in A and B are the same, they are
cleared in A, otherwise they are set in A
1 1 0 0 At
1 0 1 0 B
0 1 1 0 At+1 (A  A  B)
LOGIC MICROOPERATIONS 19

20. Insert operation
• An insert operation is used to introduce a specific bit pattern into A register, leaving
the other bit positions unchanged
• This is done as
• A mask operation to clear the desired bit positions, followed by
• An OR operation to introduce the new bits into the desired positions
• Example
• Suppose you wanted to introduce 1010 into the low order four bits of A:1101 1000 1011 0001 A (Original)
1101 1000 1011 1010 A (Desired)
• 1101 1000 1011 0001 A (Original)
1111 1111 1111 0000 Mask
1101 1000 1011 0000 A (Intermediate)
0000 0000 0000 1010 Added bits
1101 1000 1011 1010 A (Desired)
LOGIC MICROOPERATIONS 20

21. LOGIC MICROOPERATIONS 21