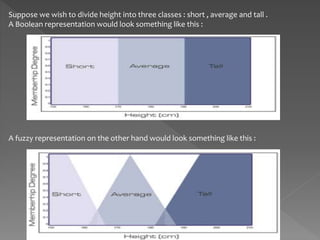
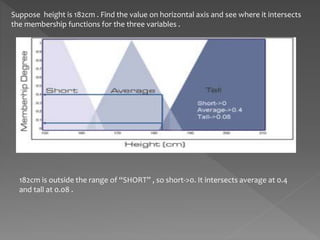
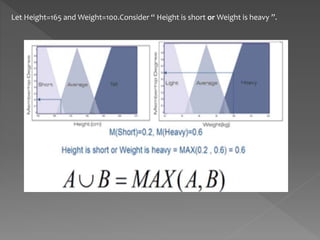
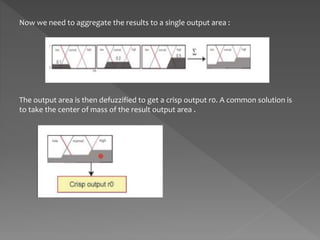
The document discusses propositions, defining them as statements with truth values that can be true or false, and includes examples to illustrate this concept. It also introduces fuzzy logic, differentiating it from classical logic by explaining its range of truth values and providing an example of how fuzzy variables are used in decision-making processes. Lastly, there is a demonstration of applying fuzzy logic in a risk assessment system based on funding and staffing levels.

1. Prepared by :
1) Drishti Bhalla − 1838
2) Dimpy Chugh − 1831

2. A PROPOSITION is a statement which has truth value: it is either true (T)
or false (F).
Example 1
Which of the following are propositions?
(a)17 + 25 = 42
(b) July 4 occurs in the winter in the Northern Hemisphere.
(c) The population of the United States is less than 250 million.
(d) Is the moon round?
(e) 7 is greater than 12.
(f) x is greater than y.
Answers
(a)is a proposition; and of course it has the 'truth value' true.
(b) is a proposition. Of course, it's false, but it's still a proposition.
(c) is a proposition, but we may not actually know whether it's true or false.
Nevertheless, the fact is that the statement itself is a proposition, because it
is definitely either true or false.
(d) is not a proposition. It's a question.
(e) is a proposition. It's false again, of course 7>12.
(f) is a bit more debatable! It's certainly a potential proposition, but until we
know the values of x and y, we can't actually say whether it is true or false.
Note that this isn't quite the same as (c), where we may not know the truth
value because we aren't well-enough informed.

4. Corresponding Tautology:
(p ∧ (p →q)) → q
Corresponding Tautology:
(¬p∧(p →q))→¬q

5. Corresponding Tautology:
((p →q) ∧ (q→r))→(p→ r)
Corresponding Tautology:
(¬p∧(p ∨q))→q

6. Corresponding Tautology:
(p∧q) →p
Corresponding Tautology:
p →(p ∨q)

7. Corresponding Tautology:
((¬p ∨ r ) ∧ (p ∨ q)) →(q ∨ r)

9. SOL:
•If the butler is telling the truth, then by (a) the cook is telling the truth.
•If the cook is telling the truth, then by (b) the gardener is lying.
•If the gardener is lying, then by (c) the handyman is telling the truth.
•If the handyman is telling the truth, they by (d) the cook is lying.
This leads to a contradiction (the cook can not be both telling the truth and
lying)! Therefore the butler and cook must be lying.
But this can also be solved by using the rules of inference

10. Let B be ‘the butler is telling the truth’, C be ‘the cook is telling the truth’, G be ‘the gardener is
telling the truth’, H be ‘the handyman is telling the truth’
The given premises are:
(1) B  C
(2) ~ (C  G) = ~C V ~G
(3) ~ (~G  ~H) = G V H
(4) H  ~C
Assume that C is true.
(5) C
From (5) and (2) by Disjunctive Syllogism
we conclude
(6) ~G
From (6) and (3) by Disjunctive Syllogism
we conclude
(7) H
From (7) and (4) by Modus Ponens
we conclude
(8) ~C
This conclusion contradicts the assumption that C is true, therefore C is false,
i.e. ~C is true.
Therefore, we can conclude that the cook is lying
Next, we use ~C in conjunction with the given premises to derive new conclusions.
(9) ~C
From (9) and (1) by Modus Tollens we conclude
(10) ~B
Therefore the butler is lying

11. SOL: Let and be the statements that and ,
respectively, so that and are the statements that and
, respectively.
this is the statement that . If A is a knight, then he is telling the truth
when he says that B is a knight, so that , and A and B are the same
type. However, if B is a knight, then B’s statement that A and B are of opposite
types, the statement would have to be true, which it is not,
because A and B are both knights. Consequently, we can conclude that A is not
a knight, that is, that .
Then because everything a knave says is false, A’s statement that B is a knight,
that is, that , is a lie. This means that and B is also a knave.
Furthermore, if B is a knave, then B’s statement that A and B are opposite types
is a lie, which is consistent with both A and B being knaves.

13.  A fuzzy logic proposition, P, is a statement involving some concept without clearly
defined boundaries .
 Fuzzy logic is a form of many-valued logic ; it deals with reasoning that is
approximate rather than fixed and exact. Fuzzy logic variables may have a truth
value that ranges in degree between 0 and 1 rather than usual true(1) or false(0).
 Main difference between classical propositions and fuzzy propositions: –
The range of their truth values : [0, 1] .
bool speed;
get the speed
if ( speed == 0) {
// speed is slow
}
else {
// speed is fast
}
float speed;
get the speed
if ((speed >= 0.0)&&(speed < 0.25)) {
// speed is slowest
}
else if ((speed >= 0.25)&&(speed < 0.5))
{
// speed is slow
}
else if ((speed >= 0.5)&&(speed < 0.75))
{
// speed is fast
}
else // speed >= 0.75 && speed < 1.0
{
// speed is fastest
}

14. Suppose we wish to divide height into three classes : short , average and tall .
A Boolean representation would look something like this :
A fuzzy representation on the other hand would look something like this :

15. Suppose height is 182cm . Find the value on horizontal axis and see where it intersects
the membership functions for the three variables .
182cm is outside the range of “SHORT” , so short->0. It intersects average at 0.4
and tall at 0.08 .

16. OR : MAX(A,B)
AND : MIN(A,B)
NOT : ¬A=1-A

17. Let Height=165 and Weight=100.Consider “ Height is short or Weight is heavy ”.

19. Suppose we want to design A risk-assessment system for some form of project . We
wish to determine the risk depending on project funding and staffing.
1. The first step is to design fuzzy variables , which are funding , staffing, and risk .For
each of these variables, we define the membership functions :

20. The next step is to define the rules for the system , using these variables. For instance
, we have :
1. If funding is adequate or staffing is small , then risk is low.
2. If funding is marginal and staffing is large then risk is normal.
3. If funding is inadequate then risk is high.
Suppose we have a funding of f0 and a staffing of s0 people. What would the risk r0
be ?

21. We have mapped the ‘crisp’ (i.e. raw values ) f0 and s0 to the membership functions
and found (for instance) that f0 has a 0.5 membership degree of “inadequate” and a
0.2 membership degree of “marginal”. The same way s0 has a 0.1 membership degree
of “small” and a 0.7 membership degree of “large”.
The next step is to evaluate the basic rules we defined :

22. Now we need to aggregate the results to a single output area :
The output area is then defuzzified to get a crisp output r0. A common solution is
to take the center of mass of the result output area .

23. THANK YOU !!!