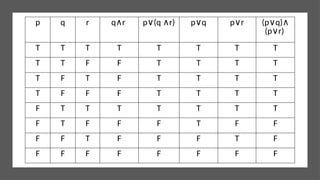
Logical equivalence refers to two propositional expressions that have the same truth value—both true or both false. The equivalence is denoted as p ≡ q and is established through methods like truth tables. In discrete mathematics, logical equivalences can be demonstrated, for instance, through the conjunction and disjunction operators.

1. Logical
Equivalence

2. LOGICAL EQUIVALENCE
Two propositional expressions are logically equivalent if they
mean the same thing. In logic, this means that the expressions
are either both true or both false.
We're probably familiar with the commutative law of addition.
One form is, "For any natural numbers x and y, x + y = y + x".
These mathematical expressions are considered equivalent
because
x + y always has the same value as y + x.

3. LOGICAL EQUIVALENCES IN DISCRETE
MATHEMATICS
Compound propositions that have the same truth values in all
possible cases are called logically equivalent. We can also define this
notion as follows.
The compound propositions p and q are called logically equivalent if
p ↔ q is a tautology(if it is always true). The notation p ≡ q denotes
that p and q are logically equivalent.
So, we can say, Logical equivalence is a type of relationship between
two statements or sentence.

4. LOGICAL EQUIVALENCES IN DISCRETE
MATHEMATICS
The only way we have so far to prove that two propositions are
equivalent is a truth table. Truth Table: A diagram in rows and
columns showing how the truth or falsity of a proposition varies with
that of its components.
Or A diagram of the outputs from all possible combinations of input.
Demonstration that p (q r)and (p q) (p r) are logically
∨ ∧ ∨ ∧ ∨
equivalent.

5. p q r q r
∧ p (q r)
∨ ∧ p q
∨ p r
∨ (p q)
∨ ∧
(p r)
∨
T T T T T T T T
T T F F T T T T
T F T F T T T T
T F F F T T T T
F T T T T T T T
F T F F F T F F
F F T F F F T F
F F F F F F F F

6. Operations On the above table:
• The Conjunction Operator: The binary conjunction operator “ ”
∧
(AND) combines two propositions to form their logical
conjunction. (If one of the input false, then output will false.)
• The Disjunction Operator: The binary disjunction operator “ ”
∨
(OR) combines two propositions to form their logical disjunction.
(If one of the input True, then output will true.)