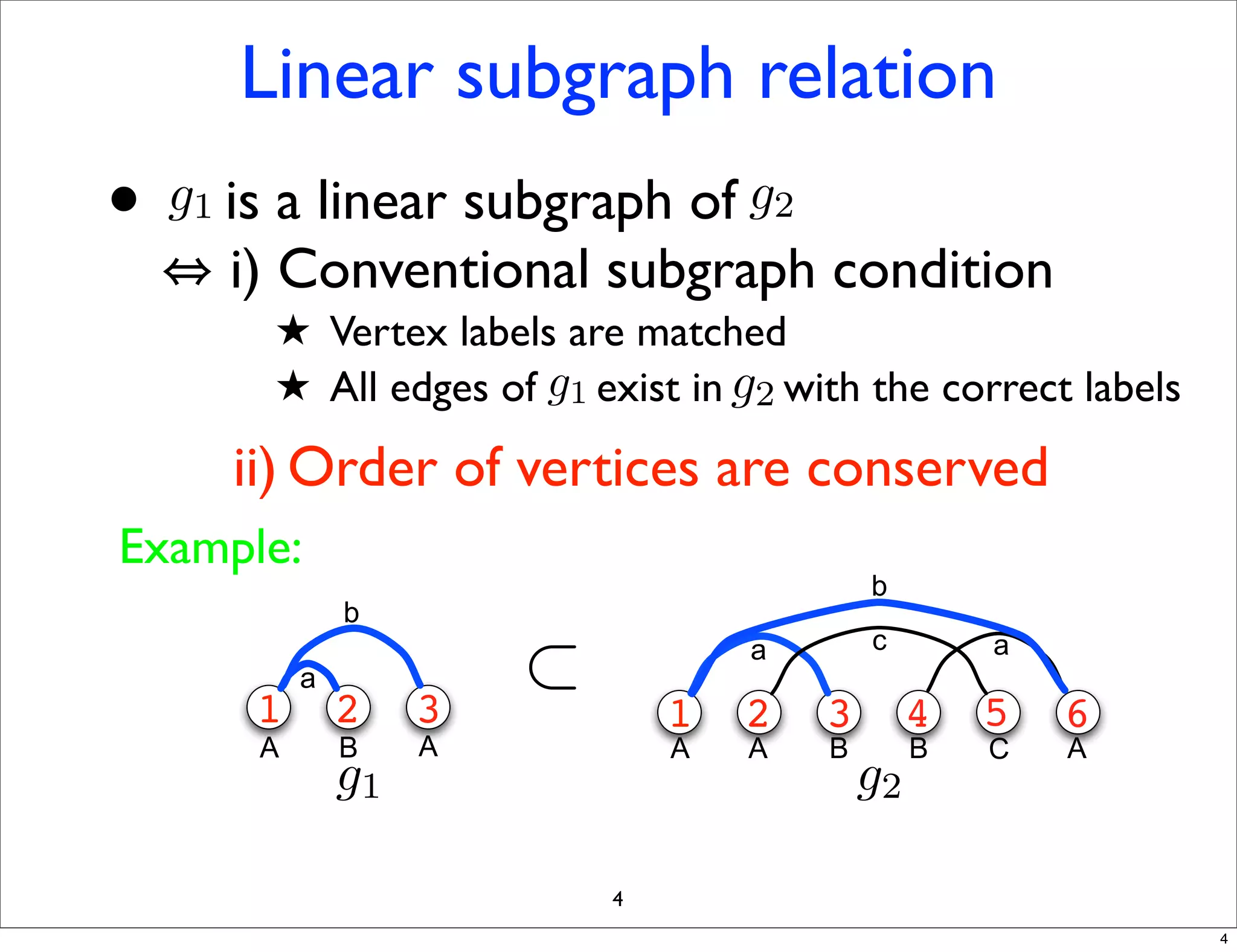
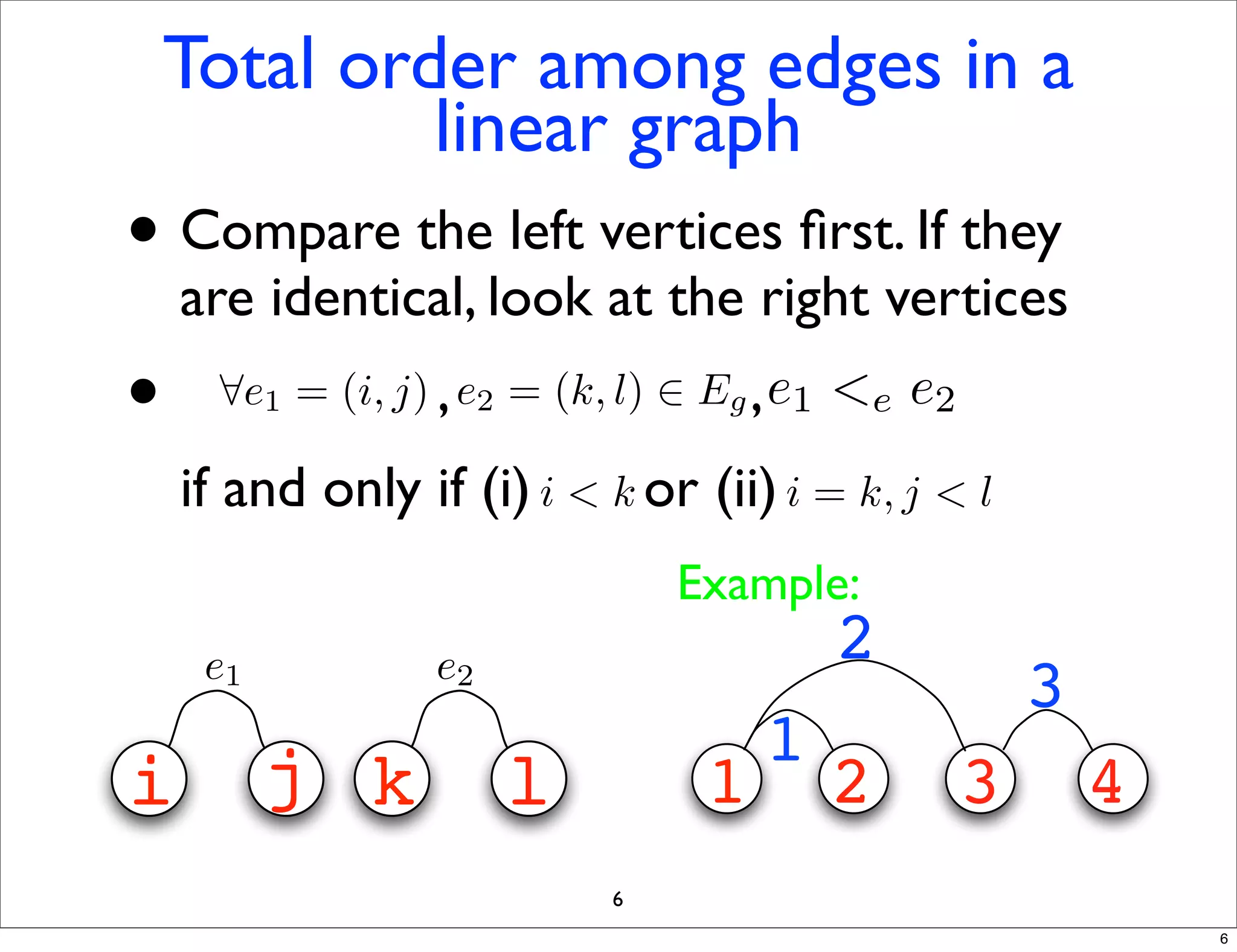
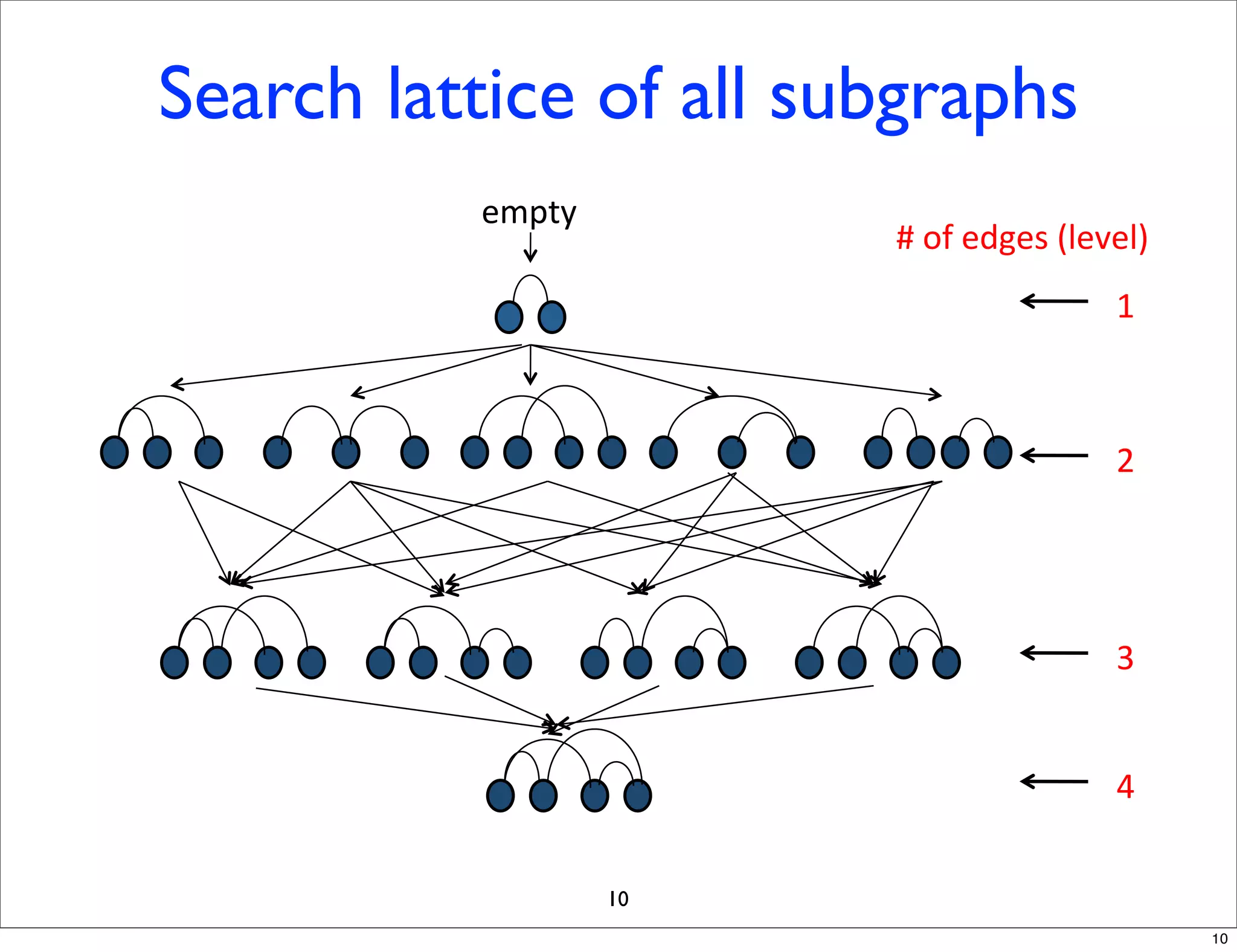
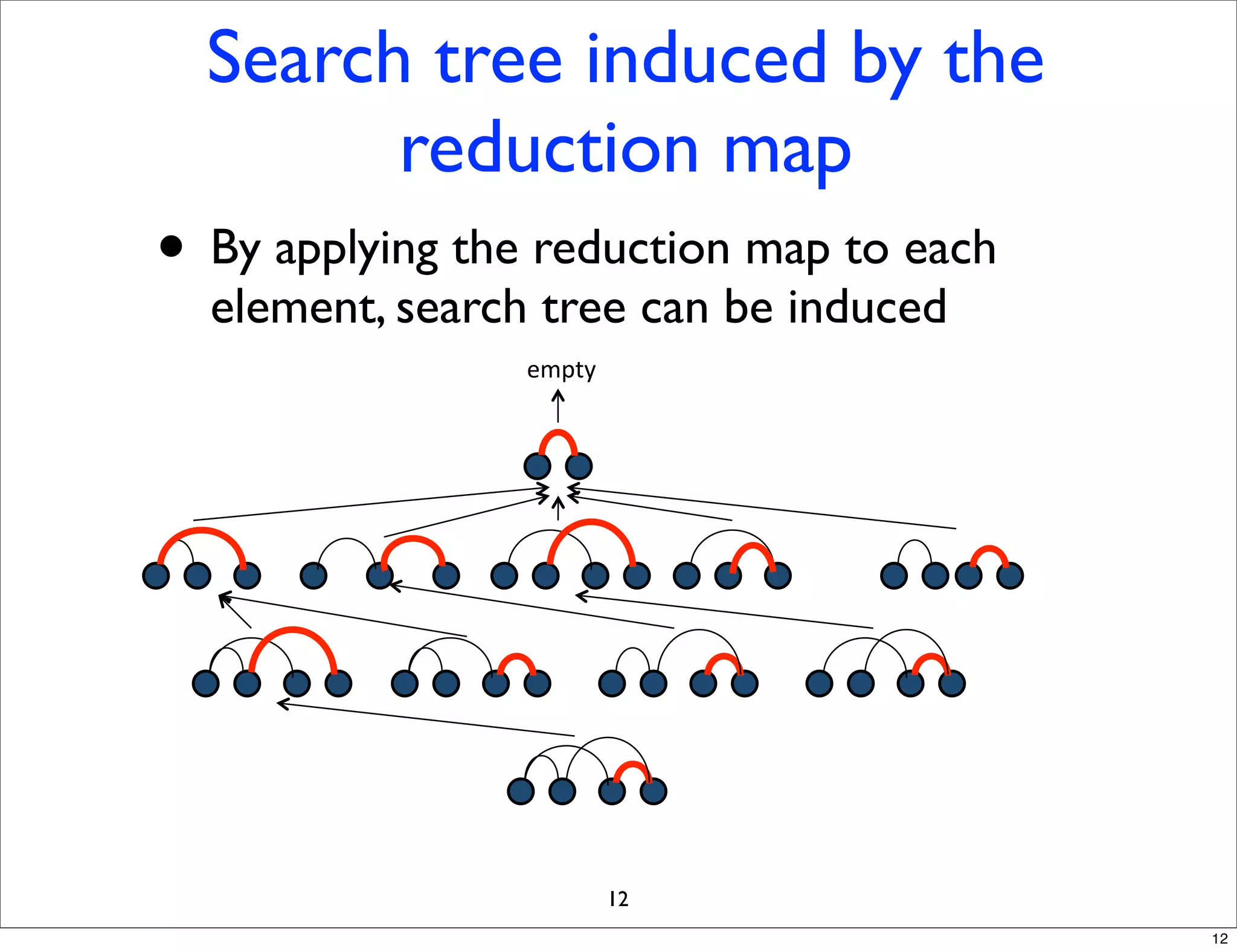
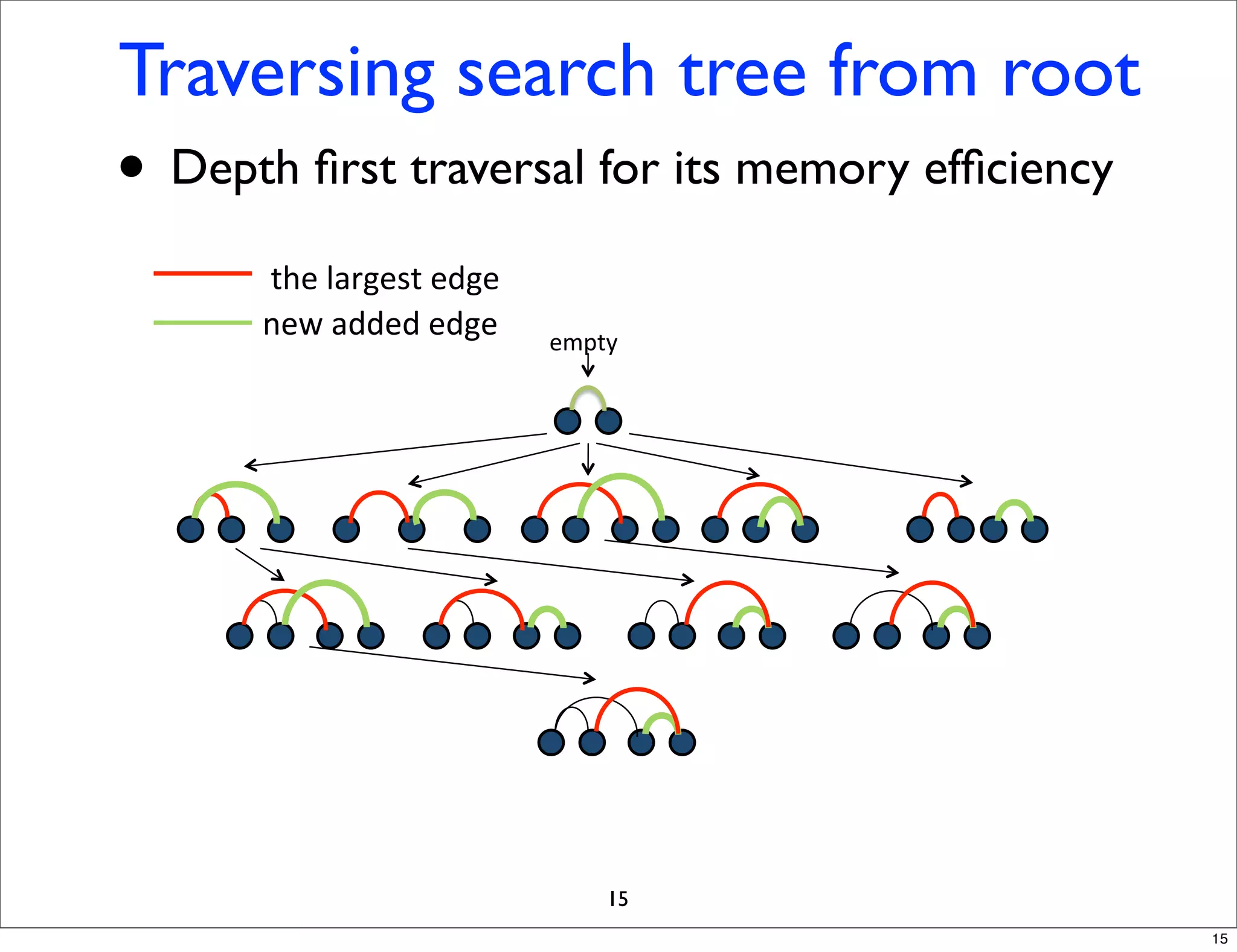
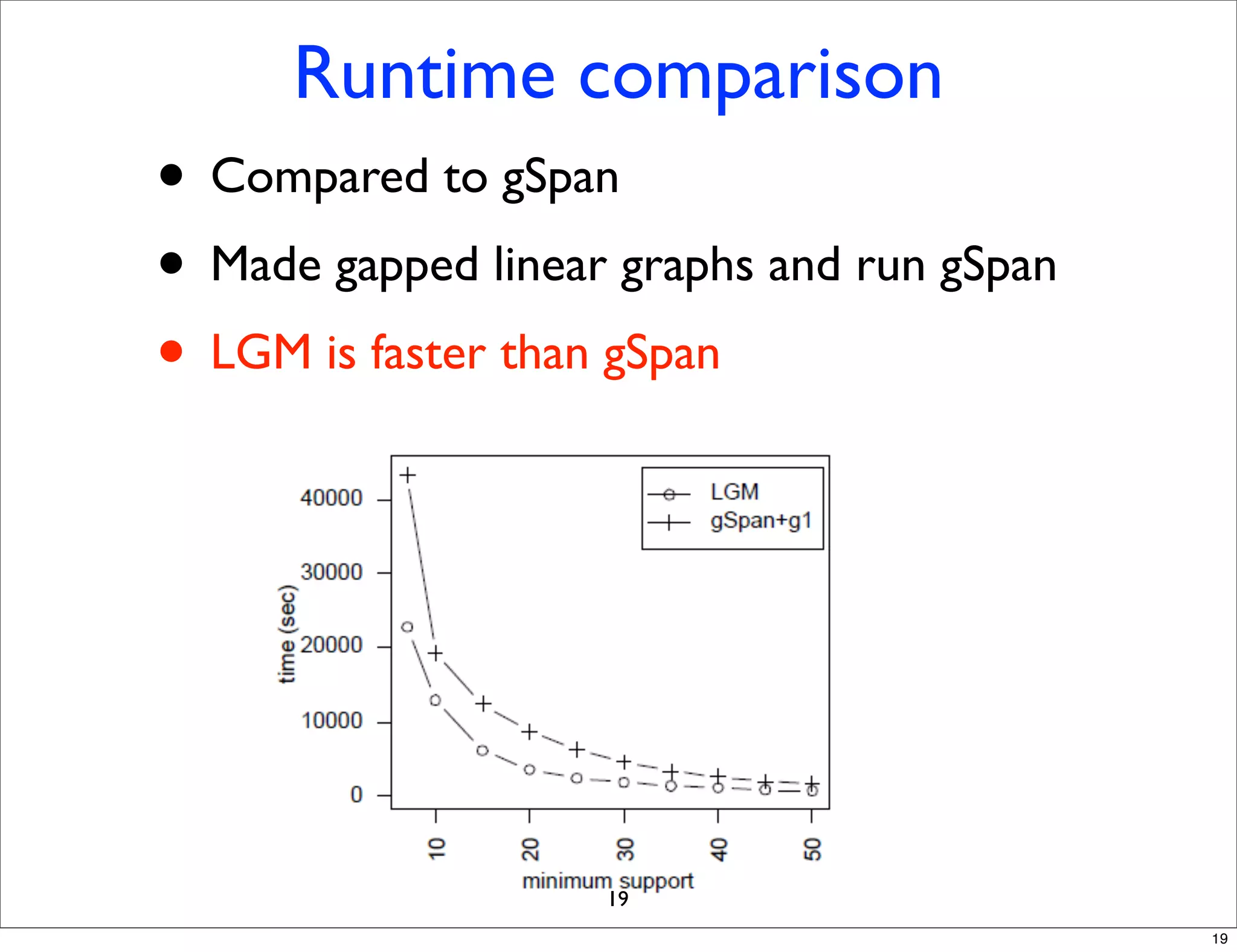
LGM is an algorithm that efficiently mines frequent subgraphs from a set of linear graphs. It uses a reverse search approach to enumerate all subgraphs without duplication, defining a search tree with a reduction map. By inverting the reduction map, it can extend patterns from parent to children nodes. Experiments apply LGM to mine motifs from protein structures, finding statistically significant patterns associated with thermophilic or mesophilic functions.

1. The 15th Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD2011)
25 May 2011
LGM: Mining Frequent Subgraphs
from Linear Graphs
Yasuo Tabei
ERATO Minato Project
Japan Science and Technology Agency
joint work with
Daisuke Okanohara (Preferred Infrastructure),
Shuichi Hirose (AIST),
Koji Tsuda (AIST)
1
1

2. Outline
• Introduction to linear graph
★ Linear subgraph relation
★ Total order among edges
• Frequent subgraph mining from a set of
linear graphs
• Experiments
★ Motif extraction from protein 3D
structures
2
2

3. Linear graph (Davydov et al., 2004)
• Labeled graph whose vertices are totally
ordered
• Linear graph g = (V, E, L , L ) V E
‣ V ⊂ N : ordered vertex set
‣ E ⊆ V × V : edge set
‣ LV → ΣV : vertex labels
‣L →Σ
E E : edge labels
Example:
c
b
a a
1 2 3 4 5 6
A B A B C A
3
3

4. Linear subgraph relation
• g1 is a linear subgraph of g2
i) Conventional subgraph condition
★ Vertex labels are matched
★ All edges of g1 exist in g2 with the correct labels
ii) Order of vertices are conserved
Example:
b
b
c
1
a
2 3
⊂ a a
1 2 3 4 5 6
A B A A A B B C A
g1 g2
4
4

5. Subgraph but not linear
subgraph
• g1 is a subgraph of g2
★ vertex labels are matched
★ all edges in g1also exist in g2 with
correct labels
• g1 is not a linear subgraph of g2
★ the order of vertices is not conserved
b
b c a
c
1 2 3 1 2 3 4
A A B A A B A
g1 g2
5
5

6. Total order among edges in a
linear graph
• Compare the left vertices first. If they
are identical, look at the right vertices
• ∀e1 = (i, j) , e2 = (k, l) ∈ Eg , e1 <e e2
if and only if (i) i < k or (ii) i = k, j < l
Example:
e1 e2 2
3
1
i j k l 1 2 3 4
6
6

7. Outline
• Introduction to linear graph
★ linear subgraph relation
★ Total order among edges
• Frequent subgraph mining from a set of
linear graphs
• Experiments
★ Motif extraction from protein 3D
structures
7
7

8. Frequent subgraph mining
from linear graphs
• Enumerate all frequent subgraphs from a set of
linear graphs
★ Subgraphs included in a set of linear graphs at
least τ times (minimum support threshold)
★ Enumerate connected and disconnected subgraphs
with a unified framework
★ Use reverse search for an efficient enumeration
(Avis and Fukuda, 1993)
• Polynomial delay
★ gSpan = exponential delay
8
8

9. Enumeration of all linear
subgraph of a linear graph
• Before considering a mining
algorithm, we have to solve the
problem of subgraph enumeration
first
• How to enumerate graph withoutof
the following linear
all subgraphs
duplication
9
9

10. Search lattice of all subgraphs
!"#$%
*+,-+!./!0+12!3!24
&
'
(
)
10
10

11. Reverse search (Avis and Fukuda, 1993)
• To enumerate all subgraphs without
duplication, we need to define a search tree
in the search lattice
• Reduction map f
★ Mapping from a child to its parent
★ Remove the largest edge
2 3
f 2
1 1
1 2 3 4 1 2 3
11
11

12. Search tree induced by the
reduction map
• By applying the reduction map to each
element, search tree can be induced
!"#$%
12
12

13. Inverting the reduction map f −1
• When traversing the tree from the root,
children nodes are created on demand
• In most cases, the inversion of reduction
map takes the following two steps:
★ Consider all children candidates
★ Take the ones that qualify the reduction map
• However, in this particular case, the
reduction map can be inverted explicitly
★ Can derive the pattern extension rule
(parent to children)
13
13

14. Pattern extension rule
14
14

15. Traversing search tree from root
• Depth first traversal for its memory efficiency
$&!'()*+!,$'!-+!
.!/')--!-'!-+! !"#$%
15
15

16. Frequent subgraph mining
• Basic idea: find all possible extensions of a
current pattern in the graph database, and
extend the pattern
• Occurrence list L G (g)
★ Record every occurrence of a pattern g in
the graph database G
★ Calculate the support of a pattern g by the
occurrence list !"#$%&'($""
• Usesupport for pruningof
the
anti-monotonicity
)$*+,+-
16
16

17. Outline
• Introduction to linear graph
★ linear subgraph relation
★ Total order among edges
• Frequent subgraph mining from a set of
linear graphs
• Experiments
★ Motif extraction from protein 3D
structures
17
17

18. Motif extraction from protein
3D structures
• Pairs of homologous proteins in thermophilic
organism and mesophilic organism
• Construct a linear graph from a protein
★ Use vertex order from N- to C- terminal
★ Assign vertex labels from {1,...,6}
★ Draw an edge between pairs of amino acid
residues whose distance is 5Å
• # of data:742, avg. # of vertices:371, avg. # of edges:
496
• Rank the enumerated patterns by statistical
significance (p-value)
★ Association to thermophilic/methophilic labels
★ Fisher exact test
18
18

19. Runtime comparison
• Compared to gSpan
• Made gapped linear graphs and run gSpan
• LGM is faster than gSpan
19
19

20. • Minimum support = 10
• 103 patterns whose p-value < 0.001
•★Thermophilic (TATA), Mesophilic (pol II)
Share the function as DNA binding
protein, but the thermostatility is
different
20
20

21. Mapping motifs in 3D structure
• Thermophilic (TATA), Mesophilic (pol II)
21
21

22. Summary
• Efficient subgraph mining algorithm from
linear graphs
• Search tree is defined by reverse search
principle
• Patterns include disconnected subgraphs
• Computational time is polynomial-delay
• Interesting patterns from proteins
22
22