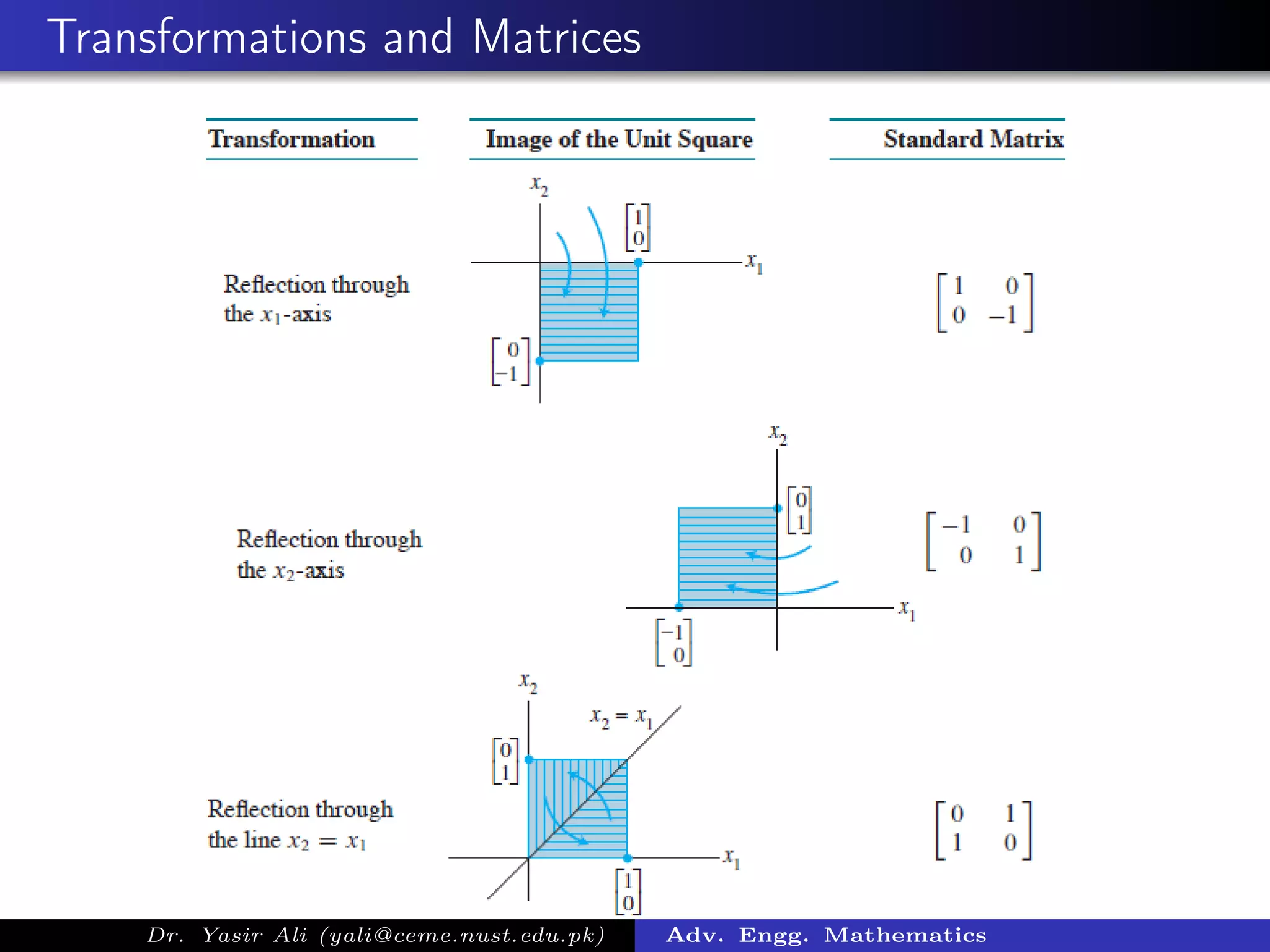
The document discusses linear transformations between vector spaces. It defines a linear transformation as a mapping between vector spaces that satisfies two conditions: 1) it is additive and 2) it is homogeneous. It also defines the kernel as the set of vectors that map to the zero vector, and the image as the set of vectors in the target space that are the image of vectors in the domain space. The document is about linear transformations presented by Dr. Yasir Ali for an advanced engineering mathematics course.

1. Adv. Engg. Mathematics
MTH-812 Linear Transformations
Dr. Yasir Ali (yali@ceme.nust.edu.pk)
DBS&H, CEME-NUST
November 6, 2017
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

2. Transformations
It is important to note here that solving Ax = b amounts to solving
x1c1 + x2c2 + · · · + xncn = b.
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

3. Transformations
It is important to note here that solving Ax = b amounts to solving
x1c1 + x2c2 + · · · + xncn = b.
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

4. Transformations
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

5. Transformations
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

6. Projection as Transformations
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

7. Share Transformations
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

8. Share Transformations
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

9. Share Transformations
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

10. Transformations and Matrices
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

11. Transformations and Matrices
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

12. Linear Transformations
Let V and U be vector spaces over the same field R. A mapping
T : V → U is called a linear transformation if it satisfies the
following two conditions:
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

13. Linear Transformations
Let V and U be vector spaces over the same field R. A mapping
T : V → U is called a linear transformation if it satisfies the
following two conditions:
1 For any vectors v, w ∈ V ,
T(v) + T(w) = T(v + w).
2 For any scalar k and vector v ∈ V ,
T(kv) = kT(v).
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

14. Linear Transformations
Let V and U be vector spaces over the same field R. A mapping
T : V → U is called a linear transformation if it satisfies the
following two conditions:
1 For any vectors v, w ∈ V ,
T(v) + T(w) = T(v + w).
2 For any scalar k and vector v ∈ V ,
T(kv) = kT(v).
A linear mapping T : V → U is completely characterized by the condition
T(av + bw) = aT(v) + bT(w).
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

15. Linear Transformations
Let V and U be vector spaces over the same field R. A mapping
T : V → U is called a linear transformation if it satisfies the
following two conditions:
1 For any vectors v, w ∈ V ,
T(v) + T(w) = T(v + w).
2 For any scalar k and vector v ∈ V ,
T(kv) = kT(v).
A linear mapping T : V → U is completely characterized by the condition
T(av + bw) = aT(v) + bT(w).
Every linear mapping takes the zero vector into the zero
vector.
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

16. Kernel and Image of a Linear Mapping
Let F : V → U be a linear mapping. The kernel of F, written Ker(F),
is the set of elements in V that map into the zero vector 0 in U, that is,
Ker(F) = {v ∈ V |F(v) = 0}
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics

17. Kernel and Image of a Linear Mapping
Let F : V → U be a linear mapping. The kernel of F, written Ker(F),
is the set of elements in V that map into the zero vector 0 in U, that is,
Ker(F) = {v ∈ V |F(v) = 0}
The image (or range) of F, written Im(F), is the set of image points in
U; that is,
Im(F) = {u ∈ U| there exists v ∈ V for which F(v) = u}
Dr. Yasir Ali (yali@ceme.nust.edu.pk) Adv. Engg. Mathematics