The document contains teaching material for a mathematics section covering several topics:
1. It defines propositions, logical connectives like conjunction and disjunction, and quantifiers.
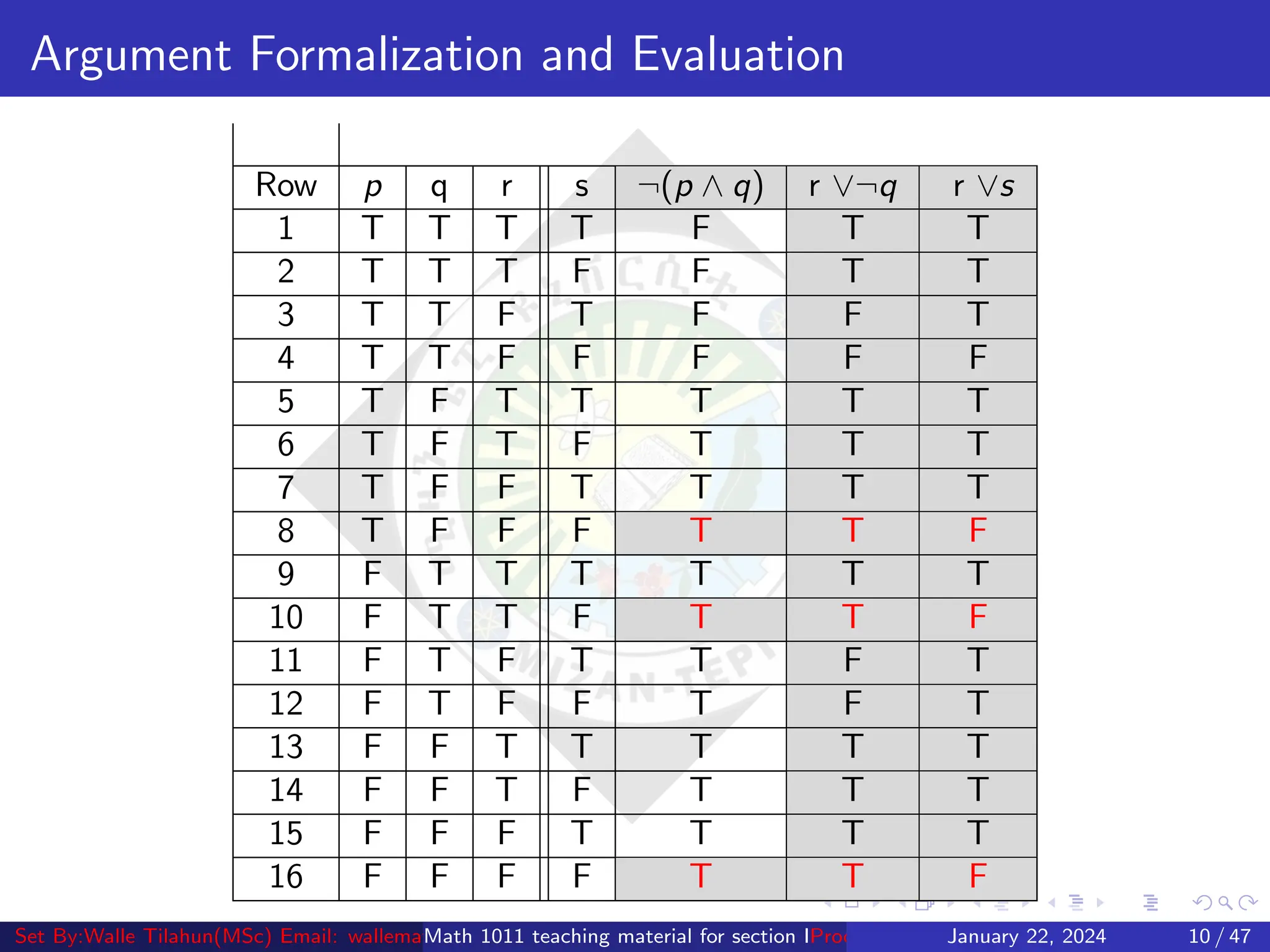
2. It discusses argument formalization and evaluation, showing an example of formalizing an argument and using a truth table to evaluate its validity.
3. It covers set theory topics like power sets, set operations like union and intersection, and using Venn diagrams to represent sets and operations.



![h
le T
Logical Connectives and Rules
Conjunction (∧)
Rule: The conjunction p ∧ q is true if and only if both p and q are true.
Disjunction (∨)
Rule: The disjunction p ∨ q is true if at least one of p or q is true.
Negation (¬)
Rule: The negation ¬p is true if and only if p is false.
Implication (→)
Rule: The implication p → q is false only when p is true and q is false.
Biconditional (↔)
Rule: The biconditional p ↔ q is true if and only if p and q have the
same truth value.
Suppose the truth values of p,q,andr are T,F,and F
respectively,then the truth value of (¬p ∨ q) → [q ↔ (p ∧ r)]is
. . . . . .
Set By:Walle Tilahun(MSc) Email: wallemath2004@gmail.com If there is error reply me!
Math 1011 teaching material for section IProofs and Examples are not included under this M
January 22, 2024 4 / 47](https://image.slidesharecdn.com/not-240124152251-6497774c/75/not-pdf-freshman-Mathematics-math1011-4-2048.jpg)