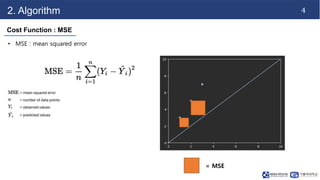
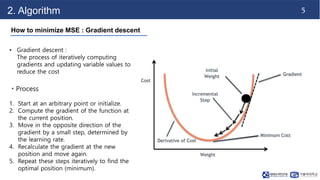
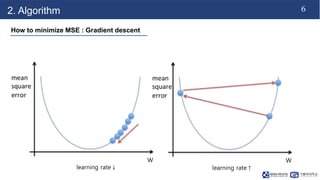
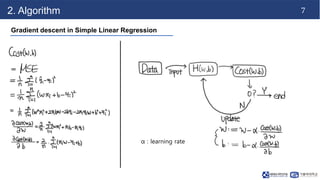
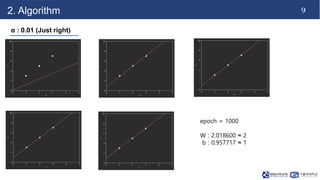
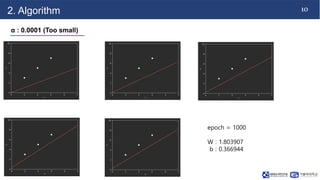
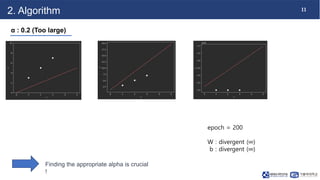
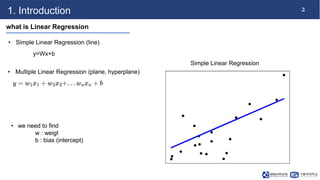
This document discusses linear regression. It begins with an introduction to simple and multiple linear regression models. It then covers the algorithm, including defining the hypothesis as y=Wx+b, initializing weights and biases, and using a cost function of mean squared error (MSE). It describes minimizing MSE through gradient descent, iterating to find optimal weights and biases. Code examples demonstrate finding the right learning rate. Advantages include fast learning and handling large datasets, while disadvantages are unclear coefficient values and difficulty with interrelated features.

1. Jin-Woo Jeong
Network Science Lab
Dept. of Mathematics
The Catholic University of Korea
E-mail: zeus0208b@gmail.com

2. 1
 Introduction
• What is Linear Regression
 Algoritm
• Hypothesis
• Cost function : MSE
• How to minimize MSE
• Codes
 Advantage / Disadvantage
• Advantage
• Disadvantage
 Q / A

3. 2
1. Introduction
what is Linear Regression
• Simple Linear Regression (line)
• Multiple Linear Regression (plane, hyperplane)
y=Wx+b
• we need to find
w : weigt
b : bias (intercept)
Simple Linear Regression

4. 3
2. Algorithm
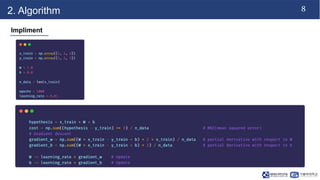
Hypothesis
• H(W,b) = Wx + b
• initialize W & b (random)
• x = [1, 2, 3]
• y = [3, 5, 7]
• initialize W = 1, b = 0

5. 4
2. Algorithm
Cost Function : MSE
• MSE : mean squared error
= MSE

6. 5
2. Algorithm
How to minimize MSE : Gradient descent
• Gradient descent :
The process of iteratively computing
gradients and updating variable values to
reduce the cost
ㆍProcess
1. Start at an arbitrary point or initialize.
2. Compute the gradient of the function at
the current position.
3. Move in the opposite direction of the
gradient by a small step, determined by
the learning rate.
4. Recalculate the gradient at the new
position and move again.
5. Repeat these steps iteratively to find the
optimal position (minimum).

7. 6
2. Algorithm
How to minimize MSE : Gradient descent
W W
learning rate↓ learning rate↑

8. 7
2. Algorithm
Gradient descent in Simple Linear Regression
α : learning rate

9. 8
2. Algorithm
Impliment

10. 9
2. Algorithm
α : 0.01 (Just right)
epoch = 1000
W : 2.018600 ≈ 2
b : 0.957717 ≈ 1

11. 10
2. Algorithm
α : 0.0001 (Too small)
epoch = 1000
W : 1.803907
b : 0.366944

12. 11
2. Algorithm
α : 0.2 (Too large)
epoch = 200
W : divergent (∞)
b : divergent (∞)
Finding the appropriate alpha is crucial
!

13. 12
3. Advantage / Disadvantage
Advantage
• The learning speed is fast.
• Training works well even with very large
datasets.
• It can learn well even when there are
many features compared to the data, and
it's easy to understand how predictions
are made.
Disadvantage
• The values of the coefficients are not
clear in terms of why they have those
specific values
• If the features in the dataset are deeply
interrelated, it becomes very difficult to
analyze the coefficients.

14. 13
4. Q & A
Q / A