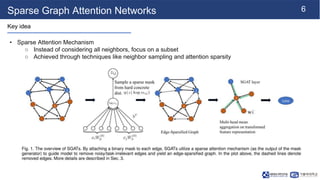
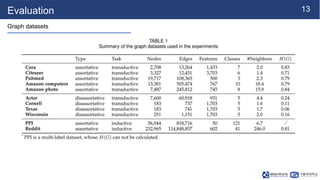
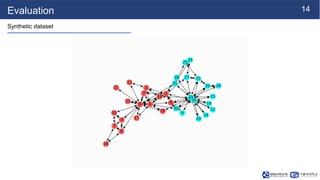
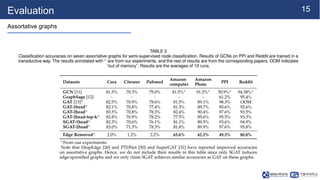
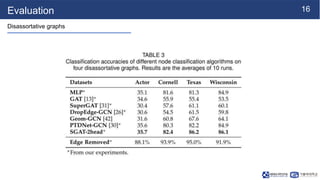
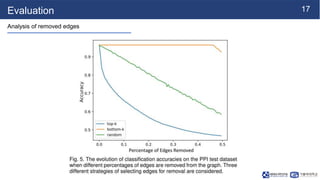
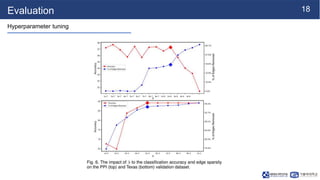
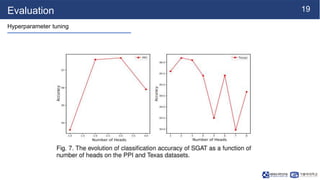
This document summarizes a research paper on sparse graph attention networks (SGATs). SGATs apply an attention mechanism to only a subset of neighbors for each node to improve the scalability and memory efficiency of graph attention networks. The key ideas are a sparse attention mechanism using techniques like neighbor sampling and a binary gate attached to each edge. SGATs show advantages in scalability, memory usage, and performance on disassortative graphs by removing up to 80% of edges while maintaining classification accuracy. Evaluation on synthetic and real-world graphs demonstrates SGATs can identify and remove noisy edges.

1. Sparse Graph Attention
Networks
Tien-Bach-Thanh Do
Network Science Lab
Dept. of Artificial Intelligence
The Catholic University of Korea
E-mail: @catholic.ac.kr
2024/02/20
Yang Ye et al.
IEEE Transactions on Knowledge and Data Engineering, 2021

2. 2
Introduction
• Graphs in Data Representation
○ Graphs model relationships between entities in data
○ Valuable for scenarios such as social networks, molecular structures, and recommendation systems
• Success of Graph Attention Networks (GATs)
○ GATs capture complex dependencies in graph-structured data
○ Demonstrate effectiveness in tasks like node classification, graph classification, and link prediction
• Scalability Challenge
○ GATs face scalability issues with large graphs
○ Computational complexity grows with the number of nodes and edges

3. 3
Background and related work
• G = (V,E) denote a graph with a set of nodes V = {v1,...,vN} connected by a set of edges E
• A denote adjacent matrix
• G graph structure
• function f(X, A, W) parameterized by W
• H is fed to a classifier to predict the class label of each unlabeled node
• To learn the model parameter W => minimize an empirical risk over all labeled nodes

4. 4
Background and related work
Neighbor Aggregation Methods
• Most graph learning algorithms follow a neighbor aggregation mechanism
• Idea: learn a parameter-sharing aggregator, which takes feature vector xi of node i and its neighbors’
feature vectors as inputs and outputs a new feature vector for node i
• 2-layer GCN, encoder function:
• The aggregator of GCNs

5. 5
Problem statement
● Challenges with GATs: discuss the limitations of GATs, such as their tendency to overfit and their poor
performance on disassortative graphs, where nodes of different types tend to connect
● Real-world graphs: explain that real-world graphs are often large and noisy, which exacerbates these
issues

6. 6
Sparse Graph Attention Networks
Key idea
• Sparse Attention Mechanism
○ Instead of considering all neighbors, focus on a subset
○ Achieved through techniques like neighbor sampling and attention sparsity

7. 7
Sparse Graph Attention Networks
Advantages
• Scalability
○ Reduces computation time and resources for large graphs
○ Enables the application of attention mechanisms to massive datasets
• Memory efficiency
○ Optimizes memory usage by computing attention only on selected neighbors
○ Particularly crucial for graphs with millions or billions of nodes

8. 8
Sparse Graph Attention Networks
Formulation
• Attach a binary gate zij to each edge
where M is the number of edges.
● To use as fewer edges as possible for semi-supervised node classification => train model parameters W
and binary masks Z by minimizing the following L0-norm regularized empirical risk
● Attention-based aggregation function

9. 9
Sparse Graph Attention Networks
Model optimization
• Stochastic Variational Optimization
• zij is subject to a Bernoulli distribution
• The hard concrete gradient estimator

10. 10
Sparse Graph Attention Networks
Model optimization
• Optimize log for each edge. Test phrase, generate a deterministic mask Z by employing the following
formula
which is the expectation of Z under the hard concrete distribution q(Z|log)

11. 11
Benefits of SGATs
● Identifying noisy/task-irrelevant edges: SGATs can identify and remove noisy or task-irrelevant edges,
allowing them to perform feature aggregation on the most informative neighbors
● Performance on disassortative graphs: superior performance of SGATs, especially on disassortative
graphs
● Edge removal: mention that SGATs can remove about 50-80% edge from large assortative graphs, while
remaining similar classification accuracies

12. 13
Evaluation
Graph datasets

13. 14
Evaluation
Synthetic dataset

14. 15
Evaluation
Assortative graphs

15. 16
Evaluation
Disassortative graphs

16. 17
Evaluation
Analysis of removed edges

17. 18
Evaluation
Hyperparameter tuning

18. 19
Evaluation
Hyperparameter tuning

19. 20
Evaluation
Visualization of learned features

20. 21
Challenges and future directions
● Trade-off
○ Fine-tuning the level of sparsity to find the right balance
○ Optimal sparsity may vary depending on the nature of the graph and the task
● Dynamic graphs
○ Extending techniques for graphs that evolve over time
○ Adapting to changes in the structure and relationships
● Benchmarking
○ Developing standardized benchmarks for evaluating Sparse GATs
○ Ensuring fair comparisons with other graph-based models

21. 22
Conclusion
● Efficient graph learning:
○ Sparse graph attention networks offer an efficient solution for large-scale graph learning
○ Balancing computational complexity with model performance is a critical consideration
● First graph learning algorithm: SGATs represent the first graph learning algorithm that shows significant
redundancies in graphs and that edge-sparsified can achieve similar or sometimes higher predictive
performances than original graphs