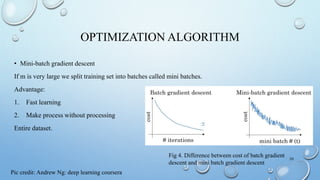
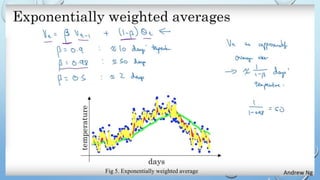
The presentation covers fundamental concepts of neural networks and deep learning, including binary classification, activation functions, loss and cost functions, and optimization algorithms. Key topics discussed are gradient descent, regularization techniques, and convolutional neural networks (CNNs) with practical examples such as cat identification. Various parameters, hyperparameters, and evaluation metrics are also highlighted to illustrate the performance and training of neural network models.

1. PRESENTATION
ON
NEURAL NETWORK &
DEEP LEARNING
BY
PAWAN SINGH
2019GI02
M.TECH IIIRD SEM
GIS CELL
UNDER THE SUPERVISION OF
DR. RAMJI DWIVEDI
ASSISTANT PROFESSOR
GIS CELL

2. INDEX
I. NEURAL NETWORK BASICS
II. BINARY CLASSIFICATION
III. SIGMOID FUNCTION/LOSS FUNCTION/COST FUNCTION
IV. GRADIENT DESCENT
V. ACTIVATION FUNCTION
VI. FORWARD AND BACKWARD PROPAGATION
VII. BIAS AND VARIANCES
VIII.REGULARIZATION
IX. OPTIMIZATION ALGORITHM(ADAM)
X. CONVOLUTION NEURAL NETWORK
2

3. NEURAL NETWORK
3
Fig 1. Basic Neuron Structure

4. ONE VARIABLE VS MULTI VARIABLE
Rate of a House (depend on one variable)
Rate of House (depend on multi variable)
4

5. MULTI- LAYER AND MULTI VARIABLE
NETWORK
5

6. BINARY CLASSIFICATION
• LET’S TAKE AN EXAMPLE OF CAT IDENTIFICATION:
• Either it is cat (1)
• Not cat(0)
• Notations: (x,y) , x ∈ real, y∈{0,1}
• For m training example- {(x(1),y(1)),(x(2),y(2)),……,(x(m),y(m))}
• X=[x(1) x(2) x(3) …..… x(m)] dim=(nX , m)
• Y=[y(1) y(2) y(3) …..Y(m)] dim=(ny , m)
6

7. 𝑦 = 𝜎 𝑤𝑇𝑥 + 𝑏
𝑦
𝜎
𝑤
𝑥
𝑏 7
Output
Sigmoid Functions
Parameters
Input Features
Bias

8. SIGMOID FUNCTIONS
• 𝜎 𝑧 =
1
1+ⅇ−𝑧 : 𝑧 = 𝑤𝑇
𝑥 + 𝑏
• If 𝑧 is large 𝜎 𝑧 = 1 &
• If 𝑧 is large negative number 𝜎 𝑧 = 0
8

9. LOSS(ERROR FUNCTION)
• 𝐿 𝑦, 𝑦 = − 𝑦 LOG 𝑦 + 1 − 𝑦 LOG 1 − 𝑦
This 𝑦 decides whether the neuron is going to activate or not
so it is also non as activation function
9

10. COST FUNCTION
• 𝐽 𝑤, 𝑏 =
1
𝑚 𝑖=1
𝑚
𝐿 𝑦 𝑖
, 𝑦 𝑖
• The loss function computes the error for a single training
example, the cost is the average of the lost function of the
entire training set.
10

11. GRADIENT DESCENT
11
Pic credit: Medium Adam: The Birthchild of AdaGrad and RMSProp | by Kaivalya
𝜕𝐽 𝑤
𝜕𝑤
< 0
Fig 2. Gradient Descent Animation

12. • Our aim is to find w , b to minimize 𝐽 𝑤, 𝑏
Repeat{
𝑤 = 𝑤 − 𝛼
𝜕𝐽 𝑤
𝜕𝑤
}
12

13. FINAL FORM
13

14. BACKWARD AND FORWARD PROPAGATION
14
𝑤 𝑙
= 𝑤 𝑙
− 𝛼 ⅆ𝜔 𝑙
𝑏 𝑙
= 𝑏 𝑙
− 𝛼 ⅆ𝑏 𝑙

15. PARAMETERS & HYPERPARAMETERS
15
Parameters Hyparameters
W Learning rate (𝛼)
b Number of iteration
Number of hidden layers
Number of hidden units
Number of choice of activations
Table 1. Parameters and Hyperparameters

16. BIAS/VARIANCE
• UNDERFITTING -- HIGH BIAS
• JUST RIGHT – JUST
• OVERFITTING – HIGH VARIANCE
16
If Training set error < Dev Set error then it is Overfit means High
Variance
If Training set error is high then it is high bias or underfitting
If training set error is high as well as dev set error is high then it is
high bias and high variance
If training set error is low as well as dev set error is low then it is
low bias and low variance.
NOTE: THERE IS ALWAYS BIAS AND VARIANCE
TRADEOFF

17. 17
Project approach in ML

18. REGULARIZATION
• Keep all the features but reduce/magnitude/values of parameter 𝜃𝑗 .
• Work well when we have a lot of features each of which contribute a bit to
predicting y .
𝐽 𝑤, 𝑏 =
1
𝑚 𝑖=1
𝑚
𝐿 𝑦 𝑖
, 𝑦 𝑖
+
𝜆
2𝑚
𝜔 2
2
+
𝜆
2𝑚
𝑏2
18
𝑤 2
2
=
𝑗=1
𝑛𝑥
𝑤𝑗
2
= 𝑤𝑇
𝑤
𝜆
2𝑚
𝑗=1
𝑛𝑥
𝑤𝑗 =
𝜆
2𝑚
𝜔 1
L2 Regularization L1 Regularization

19. OTHER REGULARIZATION
• Weight decay
• Dropout regularization
• Data augmentation
• Early stopping
19

20. OPTIMIZATION ALGORITHM
• Mini-batch gradient descent
If m is very large we split training set into batches called mini batches.
Advantage:
1. Fast learning
2. Make process without processing
Entire dataset.
20
Pic credit: Andrew Ng: deep learning coursera
Fig 4. Difference between cost of batch gradient
descent and mini batch gradient descent

21. • EXPONENTIALLY WEIGHTED AVERAGES
21
Fig 5. Exponentially weighted average

22. GRADIENT DESCENT WITH MOMENTUM
&
RMS PROP
22
Pic credit: toward data science
Fig 7. Gradient descent with Momentum

23. 𝑣ⅆ𝑏 = 𝛽𝑣ⅆ𝑏 + 1 − 𝛽 ⅆ𝑏
23
𝑣ⅆ𝑤 = 𝛽𝑣ⅆ𝑤
+ 1 − 𝛽 ⅆ𝑤
𝑠ⅆ𝑤 = 𝛽𝑠ⅆ𝑤 + 1 − 𝛽 ⅆ𝑤2
𝑠ⅆ𝑏 = 𝛽𝑠ⅆ𝑏 + 1 − 𝛽 ⅆ𝑏2
𝑤 = 𝑤 −
𝛼 ⅆ𝑤
𝑠𝑑𝑤 + 𝜖
b= b −
𝛼 ⅆ𝑏
𝑠𝑑𝑏+𝜖
Gradient descent with momentum
RMS Prop

24. ADAM OPTIMIZATION ALGORITHM
24

25. LEARNING RATE DECAY
• As the epoch passes we decreases our learning rate.
• 𝛼=1/(1+decayrate*epoch num(n))* 𝛼0
25
𝛼 = 0.95𝑛𝛼0 𝛼 =
𝑘
𝑛
𝛼0
Pic credit : stack overflow
Fig 8. Learning Rate as per loss of
function

26. EVALUATION METRICS
• PRECISION:
𝑇𝑃
𝑇𝑃+𝐹𝑃
• RECALL:
𝑇𝑃
𝑇𝑃+𝐹𝑁
• F1 SCORE:
2
1
𝑝
+
1
𝑅
26

27. CONVOLUTION NEURAL NETWORK
• CONVOLUTION:
27
Pic credit: cse19-iiith.vlabs.ac.in Fig 9. Convolution In Image

28. EDGE DETECTION FILTER
• DETECT VERTICAL EDGES
28
1 0 −1
1 0 −1
1 0 −1
1 0 −1
2 0 −2
1 0 −1
3 0 −3
10 0 −10
3 0 3
Sobel filter scharr filter

29. PADDING
• 𝑛 × 𝑛 ∗ 𝑓 × 𝑓 = 𝑛 − 𝑓 + 1 𝑛 − 𝑓 + 1
• Valid Convolution(No padding) and Same Convolution
• Same Convolution : we are going to pad so that output is same as the input size 𝑝 =
𝑓−1
2
• 𝑛 + 2𝑝 × 𝑛 + 2𝑝 ∗ 𝑓 × 𝑓 = 𝑛 + 2𝑝 − 𝑓 + 1 ∗ 𝑛 + 2𝑝 − 𝑓 + 1
29
(Size of image)*(size of filter)=size of result

30. STRIDE
• STRIDE MAKE FILTER JUMP STEPS INSTEAD OF SLIDING, STRIDE HAS TO INTEGER.
•
𝑛+2𝑝−𝑓
S
+ 1 ∗
𝑛+2𝑝−𝑓
S
+ 1
30

31. POOLING
31
Pic credit: machinelearningtutorial.net
Fig 10. Two Type of Pooling

32. PARAMETERS
• If we have 10 filters of 3*3*3 in one layer of neural network, how many parameter does the layer
have ?
• 3*3*3 = 27+bias =28 parameters
• And there are total 10 filters so 28*10=280 parameters
32

33. FINAL CNN
33
NOTE : as we go further height and width decreases but
the channel of image increases. Fig 1. Final Convolution Neural Network

34. PARAMETER
Activation shape Activation size Number of Parameters
Input (32,32,3) 3072 0
CONV1 (28,28,6) 4704 456
POOL1 (14,14,6) 1176 0
CONV2 (10,10,16) 1600 2416
POOL2 (5,5,16) 400 0
FULLY CONNECTED (400,1) 400 0
FULLY CONNETED (120,1) 120 48120
FULLY CONNECTED (84,1) 84 10164
SOFTMAX (10,1) 10 850
34
Table 2. Layers along with number of activation size and parameter

35. OTHER NETWORK
• LENET-5
• ALEX NET
• VGG
• RESNET(152)
• INCEPTION
35

36. REFERENCE
• COURSERA COURSES: ANDREW NG (MACHINE LEARNING AND DEEP LEARNING
SPECIALIZATION)
• IMPROVING THE PRICING OF OPTIONS: A NEURAL NETWORK APPROACH: ULRICH ANDERS; OLAF
KORN; CHRISTIAN SCHMITT
• CNN-BASED DIFFERENCE-CONTROLLED ADAPTIVE NON-LINEAR IMAGE FILTERS: REKECZKY,
CSABA; ROSKA, TAMÁS; USHIDA, AKIO
• A UNIFIED FRAMEWORK FOR MULTILAYER HIGH ORDER CNN : MAJORANA, SALVATORE; CHUA,
LEON O.
• A CNN HANDWRITTEN CHARACTER RECOGNIZER: H. SUZUKI; T. MATSUMOTO; LEON O. CHUA
36

37. THANK YOU
37