Lesson 26: Evaluating Definite Integrals

Section 5.3
Evaluating Deﬁnite Integrals

V63.0121.002.2010Su, Calculus I

New York University

June 21, 2010

Announcements

Final Exam is Thursday in class

Announcements

Sections 5.3–5.4 today
Section 5.5 tomorrow
Review and Movie Day
Wednesday
Final exam Thursday
roughly half-and-half
MC/FR
FR is all post-midterm
MC might have some
pre-midterm stuﬀ on it

V63.0121.002.2010Su, Calculus I (NYU) Section 5.3 Evaluating Deﬁnite Integrals June 21, 2010 2 / 44

Resurrection Policy
If your ﬁnal score beats your midterm score, we will add 10% to its weight,
and subtract 10% from the midterm weight.

Image credit: Scott Beale / Laughing Squid

Objectives

Use the Evaluation Theorem
to evaluate definite integrals.
Write antiderivatives as
indefinite integrals.
Interpret definite integrals as
“net change” of a function
over an interval.


Outline

Last time: The Definite Integral
The definite integral as a limit
Properties of the integral
Comparison Properties of the Integral

Examples

The Integral as Total Change

Indefinite Integrals
My first table of integrals

Computing Area with integrals



Definition
If f is a function defined on [a, b], the definite integral of f from a to b
is the number
b n
f (x) dx = lim f (ci ) ∆x
a n→∞
i=1

b−a
where ∆x = , and for each i, xi = a + i∆x, and ci is a point in
n
[xi−1 , xi ].

Theorem
If f is continuous on [a, b] or if f has only finitely many jump
discontinuities, then f is integrable on [a, b]; that is, the definite integral
b
f (x) dx exists and is the same for any choice of ci .
a


Notation/Terminology

b
f (x) dx
a

— integral sign (swoopy S)
f (x) — integrand
a and b — limits of integration (a is the lower limit and b the
upper limit)
dx — ??? (a parenthesis? an inﬁnitesimal? a variable?)
The process of computing an integral is called integration


Example
1
4
Estimate dx using the midpoint rule and four divisions.
0 1 + x2


Example
1
4
0 1 + x2

Solution
Dividing up [0, 1] into 4 pieces gives

1 2 3 4
x0 = 0, x1 = , x2 = , x3 = , x4 =
4 4 4 4
So the midpoint rule gives

1 4 4 4 4
M4 = 2
+ 2
+ 2
+
4 1 + (1/8) 1 + (3/8) 1 + (5/8) 1 + (7/8)2


Example
1
4
0 1 + x2

Solution

1 2 3 4
x0 = 0, x1 = , x2 = , x3 = , x4 =
4 4 4 4

1 4 4 4 4
M4 = 2
+ 2
+ 2
+
4 1 + (1/8) 1 + (3/8) 1 + (5/8) 1 + (7/8)2
1 4 4 4 4
= + + +
4 65/64 73/64 89/64 113/64


Example
1
4
0 1 + x2

Solution

1 2 3 4
x0 = 0, x1 = , x2 = , x3 = , x4 =
4 4 4 4

1 4 4 4 4
M4 = 2
+ 2
+ 2
+
4 1 + (1/8) 1 + (3/8) 1 + (5/8) 1 + (7/8)2
1 4 4 4 4
= + + +
4 65/64 73/64 89/64 113/64
150, 166, 784
= ≈ 3.1468
47, 720, 465



Theorem (Additive Properties of the Integral)
Let f and g be integrable functions on [a, b] and c a constant. Then
b
1. c dx = c(b − a)
a
b b b
2. [f (x) + g (x)] dx = f (x) dx + g (x) dx.
a a a
b b
3. cf (x) dx = c f (x) dx.
a a
b b b
4. [f (x) − g (x)] dx = f (x) dx − g (x) dx.
a a a


More Properties of the Integral

Conventions:
a b
f (x) dx = − f (x) dx
b a
a
f (x) dx = 0
a
This allows us to have
c b c
5. f (x) dx = f (x) dx + f (x) dx for all a, b, and c.
a a b


Deﬁnite Integrals We Know So Far

If the integral computes an
area and we know the area,
we can use that. For
y
instance,
1
π
1 − x 2 dx =
0 2

By brute force we computed x
1 1
1 1
x 2 dx = x 3 dx =
0 3 0 4


Theorem
Let f and g be integrable functions on [a, b].
6. If f (x) ≥ 0 for all x in [a, b], then
b
f (x) dx ≥ 0
a


Integral of a nonnegative function is nonnegative

Proof.
If f (x) ≥ 0 for all x in [a, b], then for any number of divisions n and choice
of sample points {ci }:
n n
Sn = f (ci ) ∆x ≥ 0 · ∆x = 0
i=1 ≥0 i=1

Since Sn ≥ 0 for all n, the limit of {Sn } is nonnegative, too:
b
f (x) dx = lim Sn ≥ 0
a n→∞
≥0


Theorem
b
f (x) dx ≥ 0
a

7. If f (x) ≥ g (x) for all x in [a, b], then
b b
f (x) dx ≥ g (x) dx
a a


The deﬁnite integral is “increasing”

Proof.
Let h(x) = f (x) − g (x). If f (x) ≥ g (x) for all x in [a, b], then h(x) ≥ 0
for all x in [a, b]. So by the previous property
b
h(x) dx ≥ 0
a

This means that
b b b b
f (x) dx − g (x) dx = (f (x) − g (x)) dx = h(x) dx ≥ 0
a a a a

So
b b
a a


Theorem
b
f (x) dx ≥ 0
a

7. If f (x) ≥ g (x) for all x in [a, b], then
b b
a a

8. If m ≤ f (x) ≤ M for all x in [a, b], then
b
m(b − a) ≤ f (x) dx ≤ M(b − a)
a


Bounding the integral using bounds of the function

Proof.
If m ≤ f (x) ≤ M on for all x in [a, b], then by the previous property
b b b
m dx ≤ f (x) dx ≤ M dx
a a a

By Property 1, the integral of a constant function is the product of the
constant and the width of the interval. So:
b
m(b − a) ≤ f (x) dx ≤ M(b − a)
a


Estimating an integral with inequalities

Example
2
1
Estimate dx using Property 8.
1 x



Example
2
1
1 x

Solution
Since
1 1 1
1 ≤ x ≤ 2 =⇒ ≤ ≤
2 x 1
we have
2
1 1
· (2 − 1) ≤ dx ≤ 1 · (2 − 1)
2 1 x
or
2
1 1
≤ dx ≤ 1
2 1 x


Outline


Examples





Socratic proof

The deﬁnite integral of
velocity measures
displacement (net distance)
The derivative of
displacement is velocity
So we can compute
displacement with the
deﬁnite integral or the
antiderivative of velocity
But any function can be a
velocity function, so . . .


Theorem of the Day

Theorem (The Second Fundamental Theorem of Calculus)
Suppose f is integrable on [a, b] and f = F for another function F , then
b
f (x) dx = F (b) − F (a).
a


Theorem of the Day

Theorem (The Second Fundamental Theorem of Calculus)
Suppose f is integrable on [a, b] and f = F for another function F , then
b
f (x) dx = F (b) − F (a).
a

Note
In Section 5.3, this theorem is called “The Evaluation Theorem”. Nobody
else in the world calls it that.


Proving the Second FTC

b−a
Divide up [a, b] into n pieces of equal width ∆x = as usual. For
n
each i, F is continuous on [xi−1 , xi ] and diﬀerentiable on (xi−1 , xi ). So
there is a point ci in (xi−1 , xi ) with

F (xi ) − F (xi−1 )
= F (ci ) = f (ci )
xi − xi−1

Or
f (ci )∆x = F (xi ) − F (xi−1 )


Proof continued

We have for each i
f (ci )∆x = F (xi ) − F (xi−1 )
Form the Riemann Sum:
n n
Sn = f (ci )∆x = (F (xi ) − F (xi−1 ))
i=1 i=1

= (F (x1 ) − F (x0 )) + (F (x2 ) − F (x1 )) + (F (x3 ) − F (x2 )) + · · ·
· · · + (F (xn−1 ) − F (xn−2 )) + (F (xn ) − F (xn−1 ))
= F (xn ) − F (x0 ) = F (b) − F (a)


Proof continued

We have for each i
f (ci )∆x = F (xi ) − F (xi−1 )
Form the Riemann Sum:
n n
Sn = f (ci )∆x = (F (xi ) − F (xi−1 ))
i=1 i=1

= (F (x1 ) − F (x0 )) + (F (x2 ) − F (x1 )) + (F (x3 ) − F (x2 )) + · · ·
· · · + (F (xn−1 ) − F (xn−2 )) + (F (xn ) − F (xn−1 ))
= F (xn ) − F (x0 ) = F (b) − F (a)

See if you can spot the invocation of the Mean Value Theorem!


Proof Completed

We have shown for each n,

Sn = F (b) − F (a)

so in the limit
b
f (x) dx = lim Sn = lim (F (b) − F (a)) = F (b) − F (a)
a n→∞ n→∞


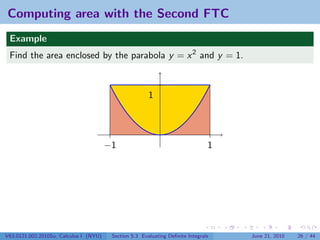
Computing area with the Second FTC

Example
Find the area between y = x 3 and the x-axis, between x = 0 and x = 1.



Example

Solution

1 1
x4 1
A= x 3 dx = =
0 4 0 4



Example

Solution

1 1
x4 1
A= x 3 dx = =
0 4 0 4

Here we use the notation F (x)|b or [F (x)]b to mean F (b) − F (a).
a a


Example
Find the area enclosed by the parabola y = x 2 and y = 1.


Example

1

−1 1


Example

1

−1 1

Solution

1 1
x3 1 1 4
A=2− x 2 dx = 2 − =2− − − =
−1 3 −1 3 3 3


Computing an integral we estimated before

Example
1
4
Evaluate the integral dx.
0 1 + x2


Example
1
4
0 1 + x2

Solution

1 2 3 4
x0 = 0, x1 = , x2 = , x3 = , x4 =
4 4 4 4

1 4 4 4 4
M4 = 2
+ 2
+ 2
+
4 1 + (1/8) 1 + (3/8) 1 + (5/8) 1 + (7/8)2
1 4 4 4 4
= + + +
4 65/64 73/64 89/64 113/64
150, 166, 784
= ≈ 3.1468
47, 720, 465



Example
1
4
0 1 + x2

Solution

1 1
4 1
dx = 4 dx
0 1 + x2 0 1 + x2



Example
1
4
0 1 + x2

Solution

1 1
4 1
dx = 4 dx
0 1 + x2 0 1 + x2
= 4 arctan(x)|1
0



Example
1
4
0 1 + x2

Solution

1 1
4 1
dx = 4 dx
0 1 + x2 0 1 + x2
= 4 arctan(x)|1
0
= 4 (arctan 1 − arctan 0)



Example
1
4
0 1 + x2

Solution

1 1
4 1
dx = 4 dx
0 1 + x2 0 1 + x2
= 4 arctan(x)|1
0
π
=4 −0
4



Example
1
4
0 1 + x2

Solution

1 1
4 1
dx = 4 dx
0 1 + x2 0 1 + x2
= 4 arctan(x)|1
0
π
=4 −0 =π
4



Example
2
1
Evaluate dx.
1 x



Example
2
1
1 x

Solution
Since
1 1 1
1 ≤ x ≤ 2 =⇒ ≤ ≤
2 x 1
we have
2
1 1
· (2 − 1) ≤ dx ≤ 1 · (2 − 1)
2 1 x
or
2
1 1
≤ dx ≤ 1
2 1 x



Example
2
1
Evaluate dx.
1 x

Solution

2
1
dx
1 x



Example
2
1
Evaluate dx.
1 x

Solution

2
1
dx = ln x|2
1
1 x



Example
2
1
Evaluate dx.
1 x

Solution

2
1
dx = ln x|2
1
1 x
= ln 2 − ln 1



Example
2
1
Evaluate dx.
1 x

Solution

2
1
dx = ln x|2
1
1 x
= ln 2 − ln 1
= ln 2


Outline


Examples






Another way to state this theorem is:
b
F (x) dx = F (b) − F (a),
a

or the integral of a derivative along an interval is the total change between
the sides of that interval. This has many ramiﬁcations:



b
F (x) dx = F (b) − F (a),
a


Theorem
If v (t) represents the velocity of a particle moving rectilinearly, then
t1
v (t) dt = s(t1 ) − s(t0 ).
t0



b
F (x) dx = F (b) − F (a),
a


Theorem
If MC (x) represents the marginal cost of making x units of a product, then
x
C (x) = C (0) + MC (q) dq.
0



b
F (x) dx = F (b) − F (a),
a


Theorem
If ρ(x) represents the density of a thin rod at a distance of x from its end,
then the mass of the rod up to x is
x
m(x) = ρ(s) ds.
0


Outline


Examples





A new notation for antiderivatives

To emphasize the relationship between antidiﬀerentiation and integration,
we use the indeﬁnite integral notation

f (x) dx

for any function whose derivative is f (x).


A new notation for antiderivatives

To emphasize the relationship between antidiﬀerentiation and integration,
we use the indeﬁnite integral notation

f (x) dx

for any function whose derivative is f (x). Thus

x 2 dx = 1 x 3 + C .
3



[f (x) + g (x)] dx = f (x) dx + g (x) dx

x n+1
x n dx = + C (n = −1) cf (x) dx = c f (x) dx
n+1
1
e x dx = e x + C dx = ln |x| + C
x
ax
sin x dx = − cos x + C ax dx = +C
ln a

cos x dx = sin x + C csc2 x dx = − cot x + C

sec2 x dx = tan x + C csc x cot x dx = − csc x + C
1
sec x tan x dx = sec x + C √ dx = arcsin x + C
1 − x2
1
dx = arctan x + C
1 + x2


Outline


Examples





Example
Find the area between the graph of y = (x − 1)(x − 2), the x-axis, and the
vertical lines x = 0 and x = 3.


Example

Solution
3
Consider (x − 1)(x − 2) dx.
0


Graph

y

x
1 2 3


Example

Solution
3
Consider (x − 1)(x − 2) dx. Notice the integrand is positive on [0, 1)
0
and (2, 3], and negative on (1, 2).


Example

Solution
3
Consider (x − 1)(x − 2) dx. Notice the integrand is positive on [0, 1)
0
and (2, 3], and negative on (1, 2). If we want the area of the region, we
have to do
1 2 3
A= (x − 1)(x − 2) dx − (x − 1)(x − 2) dx + (x − 1)(x − 2) dx
0 1 2
1 3 1 2 3
= 3x − 2 x 2 + 2x
3
0
− 1 3
3x − 3 x 2 + 2x
2 1
+ 1 3
3x − 2 x 2 + 2x
3
2
5 1 5 11
= − − + = .
6 6 6 6


Interpretation of “negative area” in motion

There is an analog in rectlinear motion:
t1
v (t) dt is net distance traveled.
t0
t1
|v (t)| dt is total distance traveled.
t0


What about the constant?

It seems we forgot about the +C when we say for instance
1 1
x4 1 1
x 3 dx = = −0=
0 4 0 4 4

But notice
1
x4 1 1 1
+C = +C − (0 + C ) = +C −C =
4 0 4 4 4

no matter what C is.
So in antidiﬀerentiation for deﬁnite integrals, the constant is
immaterial.


Summary

The second Fundamental Theorem of Calculus:
b
f (x) dx = F (b) − F (a)
a

where F = f .
Deﬁnite integrals represent net change of a function over an interval.
We write antiderivatives as indeﬁnite integrals f (x) dx


Lesson 26: Evaluating Definite Integrals

Recommended

Recommended

More Related Content

What's hot

What's hot (17)

Viewers also liked

Viewers also liked (20)

Similar to Lesson 26: Evaluating Definite Integrals

Similar to Lesson 26: Evaluating Definite Integrals (20)

More from Matthew Leingang

More from Matthew Leingang (20)

Recently uploaded

Recently uploaded (20)

Lesson 26: Evaluating Definite Integrals