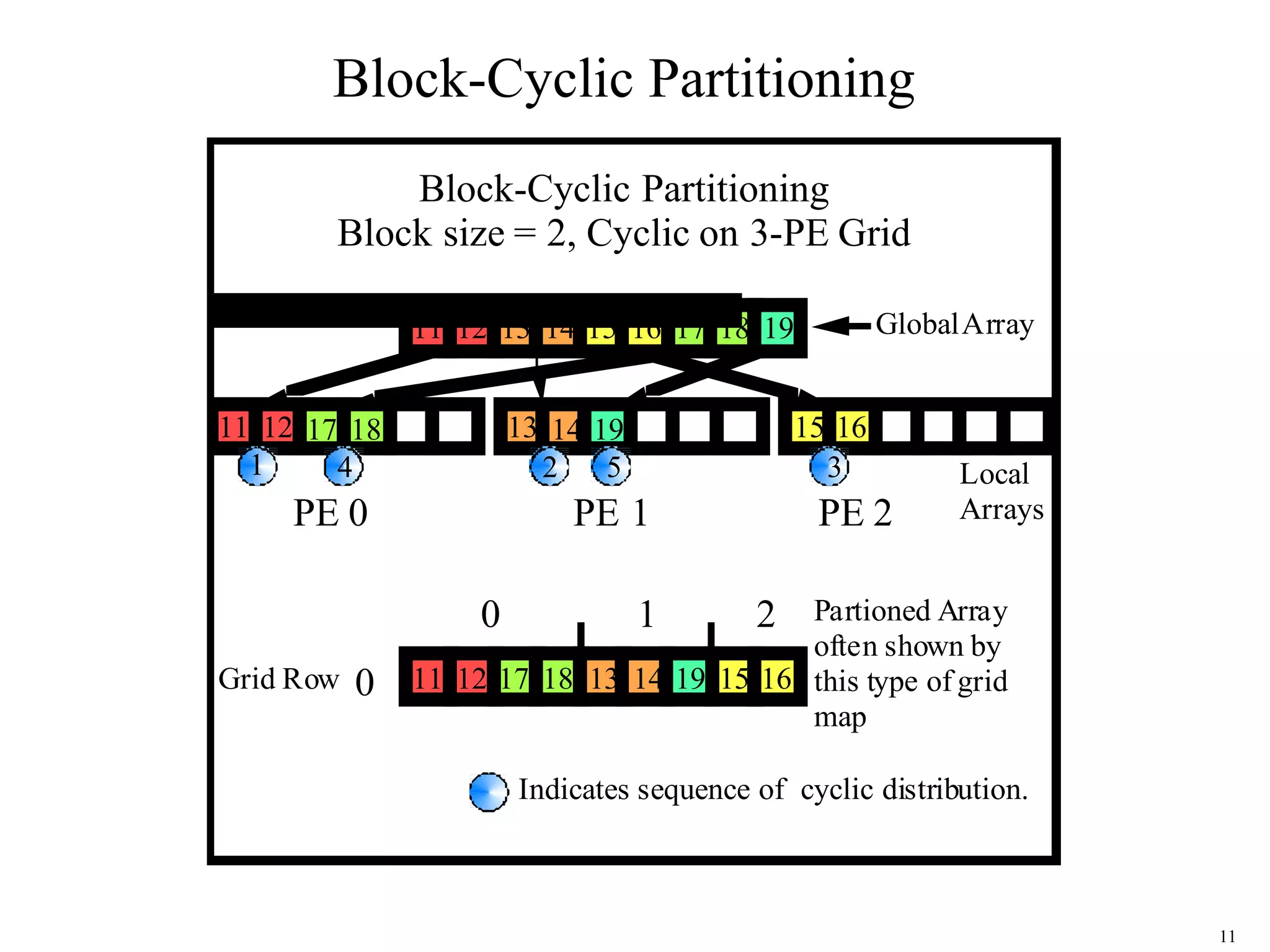
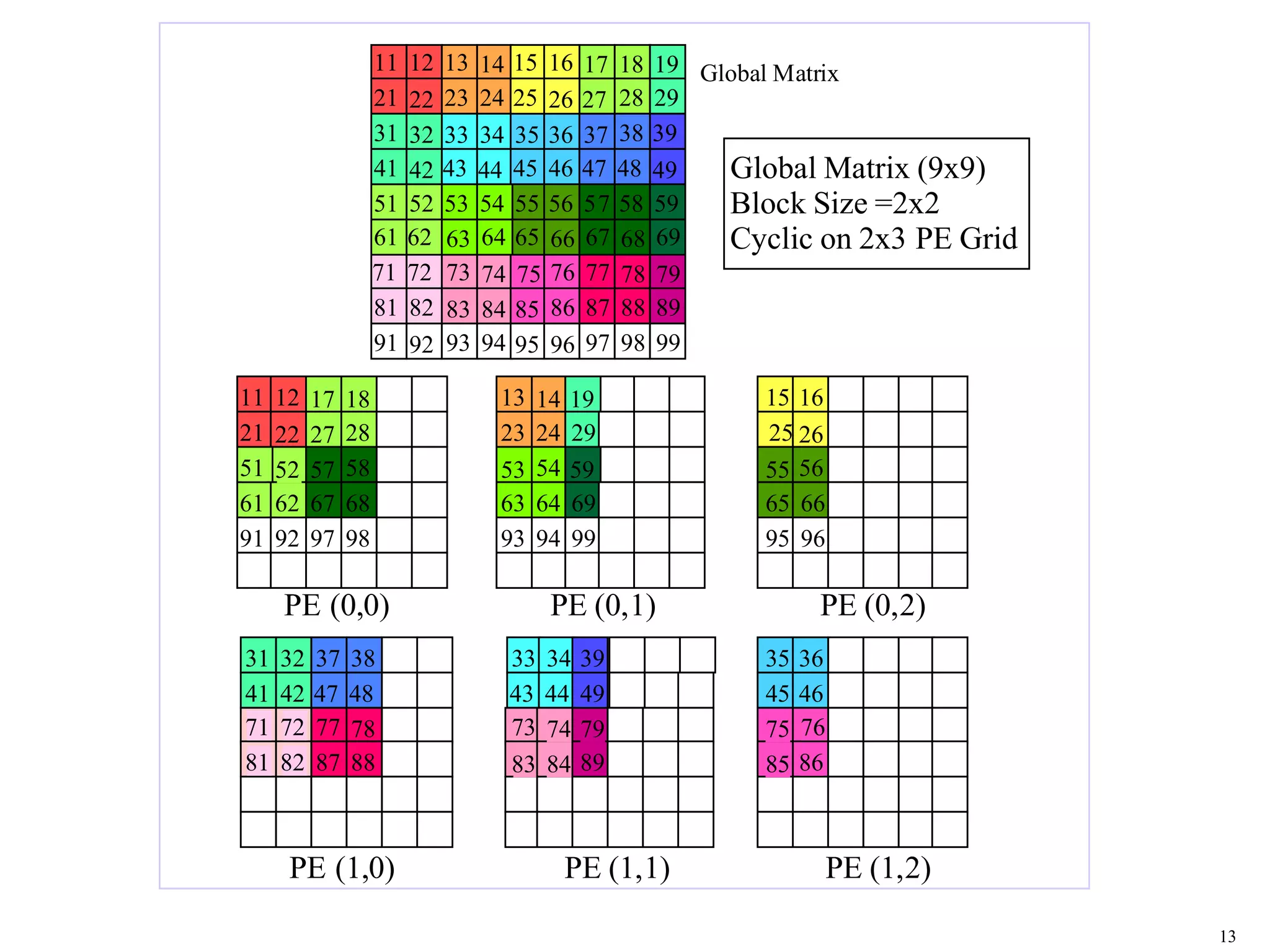
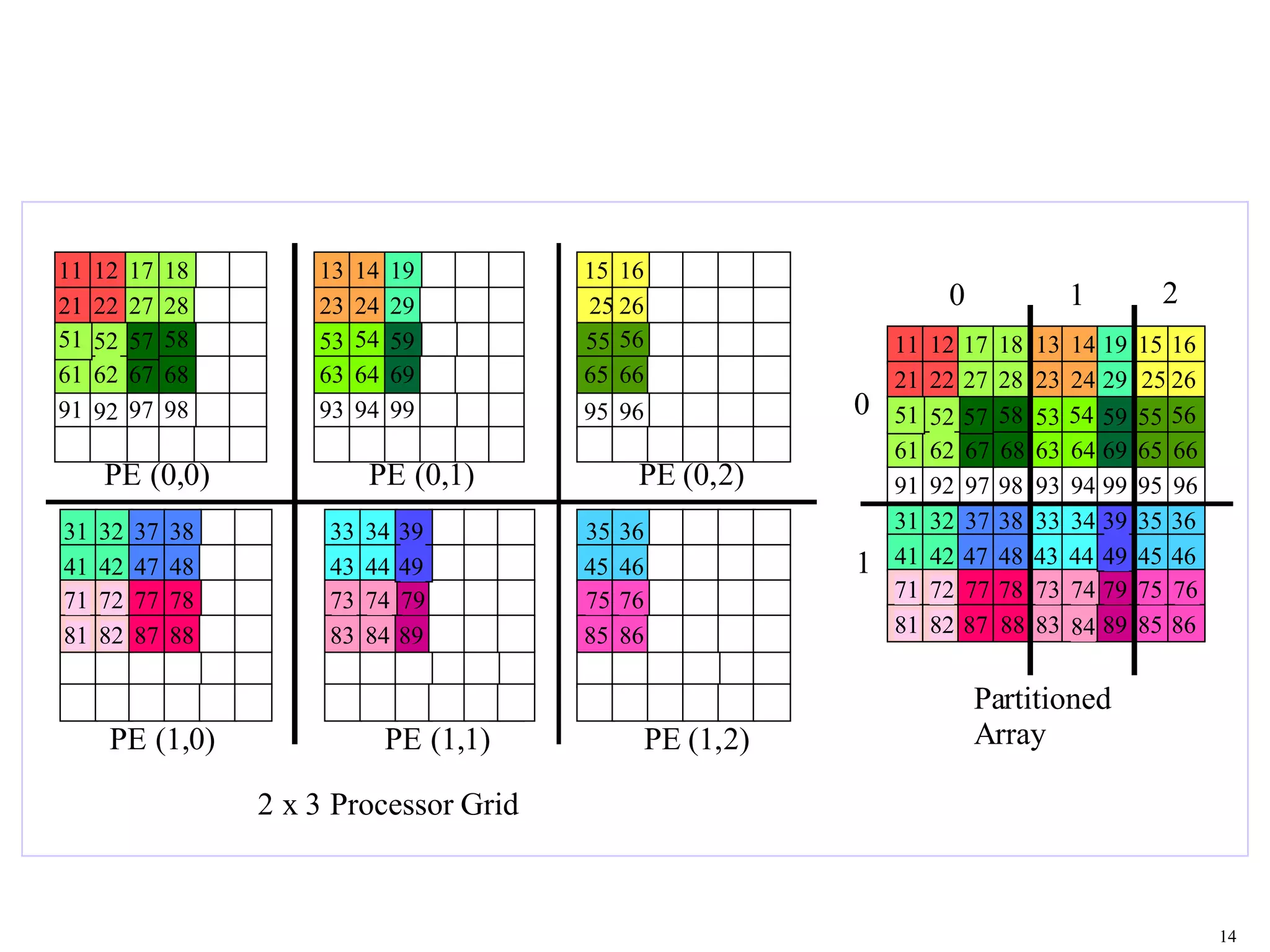
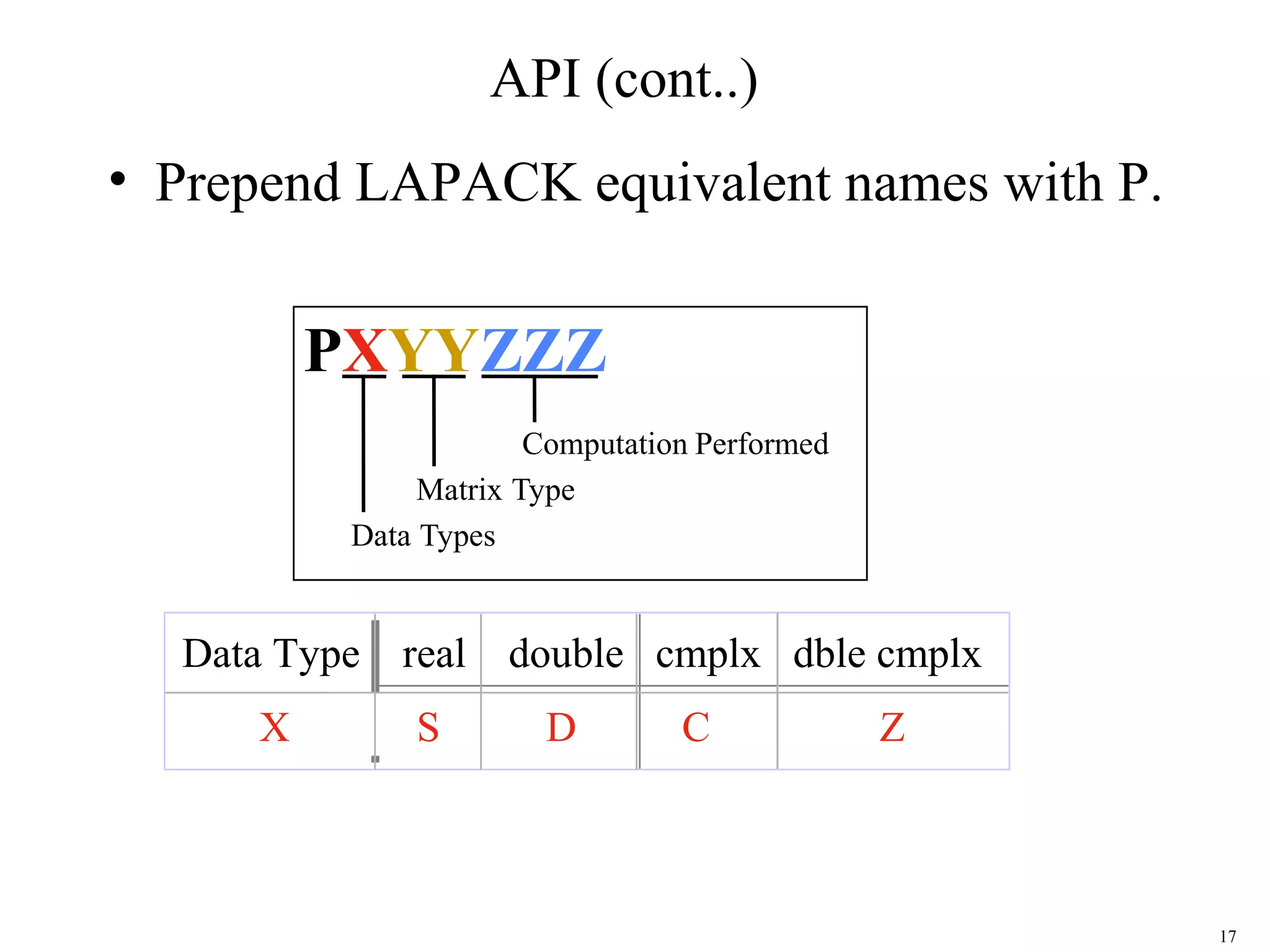
This document provides an introduction and overview of ScaLAPACK, a library of linear algebra routines for solving dense linear algebra problems in parallel. ScaLAPACK relies on BLAS, LAPACK, BLACS, and PBLAS to perform operations on dense matrices distributed across multiple processors using a 2D block cyclic distribution. Example code is provided to initialize the processor grid with BLACS, distribute a matrix and vector among processes, and solve a system of linear equations using ScaLAPACK routines.

1. Introduction to ScaLAPACK

2. 2
ScaLAPACK
• ScaLAPACK is for solving dense linear
systems and computing eigenvalues for
dense matrices

3. 3
ScaLAPACK
• Scalable Linear Algebra PACKage
• Developing team from University of
Tennessee, University of California Berkeley,
ORNL, Rice U.,UCLA, UIUC etc.
• Support in Commercial Packages
– NAG Parallel Library
– IBM PESSL
– CRAY Scientific Library
– VNI IMSL
– Fujitsu, HP/Convex, Hitachi, NEC

4. 4
Description
• A Scalable Linear Algebra Package
(ScaLAPACK)
• A library of linear algebra routines for MPP
and NOW machines
• Language : Fortran
• Dense Matrix Problem Solvers
– Linear Equations
– Least Squares
– Eigenvalue

5. 5
Technical Information
• ScaLAPACK web page
– http://www.netlib.org/scalapack
• ScaLAPACK User’s Guide
• Technical Working Notes
– http://www.netlib.org/lapack/lawn

6. 6
Packages
• LAPACK
– Routines are single-PE Linear Algebra solvers,
utilities, etc.
• BLAS
– Single-PE processor work-horse routines
(vector, vector-matrix & matrix-matrix)
• PBLAS
– Parallel counterparts of BLAS. Relies on
BLACS for blocking and moving data.

7. 7
Packages (cont.)
• BLACS
– Constructs 1-D & 2-D processor grids for
matrix decomposition and nearest neighbor
communication patterns. Uses message passing
libraries (MPI, PVM, MPL, NX, etc) for data
movement.

8. 8
Dependencies & Parallelism
of Component Packages
BLAS
LAPACK
MPI, PVM,...
BLACS
PBLAS
ScaLAPACK
Serial Parallel

9. 9
Data Partitioning
• Initialize BLACS routines
– Set up 2-D mesh (mp, np)
– Set (CorR) Column or Row Major Order
– Call returns context handle (icon)
– Get row & column through gridinfo
(myrow,mycol)
• blacs_gridinit( icon, CorR, mp, np )
• blacs_gridinfo( icon, mp, np, myrow,
mycol)

10. 10
Data Partitioning (cont.)
• Block-cyclic Array Distribution.
– Block: (groups of sequential elements)
– Cyclic: (round-robin assignment to PEs)
• Example 1-D Partitioning:
– Global 9-element array distributed on a 3-PE
grid with 2 element blocks: block(2)-cyclic(3)

11. 11
Block-Cyclic Partitioning
11 12 13 14 15 16 17 18 19
15 1611 12 17 18 13 14 19
Block-Cyclic Partitioning
Block size = 2, Cyclic on 3-PE Grid
15 1611 12 17 18 13 14 19
PE 0 PE 1 PE 2
0 2
2 34 51
GlobalArray
Local
Arrays
1 Partioned Array
often shown by
this type of grid
map
0Grid Row
Indicates sequence of cyclic distribution.

12. 12
2-D Partitioning
• Example 2-D Partitioning
– A(9,9) mapped onto PE(2,3) grid block(2,2)
– Use 1-D example to distribute column elements
in each row, a block(2)-cyclic(3) distribution.
– Assign rows to first PE dimension by block(2)-
cyclic(2) distribution.

13. 13
11
21
31
41
51
61
71
81
91
12
22
32
42
52
62
72
82
92
13 14 15 16 17 18 19
23 24 25 26 27 28 29
33 34 35 36 37 38 39
43 44 45 46 47 48 49
5453 55 56 57 58 59
63 64 65 66 67 68 69
73 74 75 76 77 78 79
83 84 85 86 87 88 89
9593 94 96 97 98 99
11
21
12
22
13 14
23 24
15 16
25 26
17 18
27 28
19
29
31
41
32
42
51
61
52
62
71
81
72
82
91 92
33 34
43 44
93 94
73 74
83 84
35 36
45 46
37 38
47 48
39
49
5453
63 64
55 56
65 66
57 58
67 68
59
69
75 76
85 86
77 78
87 88
79
89
95 9697 98 99
Global Matrix (9x9)
Block Size =2x2
Cyclic on 2x3 PE Grid
Global Matrix
PE (0,0) PE (0,1) PE (0,2)
PE (1,0) PE (1,1) PE (1,2)

14. 14
11
21
12
22
13 14
23 24
15 16
25 26
17 18
27 28
19
29
31
41
32
42
51
61
52
62
71
81
72
82
91 92
33 34
43 44
93 94
73 74
83 84
35 36
45 46
37 38
47 48
39
49
5453
63 64
55 56
65 66
57 58
67 68
59
69
75 76
85 86
77 78
87 88
79
89
95 9697 98 99
35 36
45 46
75 76
85 86
31
41
32
42
71
81
72
82
37 38
47 48
77 78
87 88
33 34
43 44
73 74
83 84
39
49
79
89
15 16
25 26
55 56
65 66
95 96
11
21
12
22
17 18
27 28
51
61
52
62
91 92
57 58
67 68
97 98
13 14
23 24
19
29
93 94
5453
63 64
59
69
99
2 x 3 Processor Grid
PE (0,0) PE (0,1) PE (0,2)
PE (1,0) PE (1,1) PE (1,2)
0 1 2
0
1
Partitioned
Array

15. 15
Syntax for descinit
OUT idesc Descriptor
IN m Row Size (Global)
IN n Column Size (Global)
IN mb Row Block Size
IN nb Column Size
IN i Starting Grid Row
IN j Starting Grid Column
IN icon BLACS context
IN mla Leading Dimension of Local Matrix
OUT ier Error number
The starting grid location is usually (i=0,j=0).
IorO arg Description
descinit(idesc, m,n, mb,nb, i,j, icon, mla, ier)

16. 16
Application Program Interfaces (API)
• Drivers
– Solves a Complete Problem
• Computational Components
– Performs Tasks: LU factorization, etc.
• Auxiliary Routines
– Scaling, Matrix Norm, etc.
• Matrix Redistribution/Copy Routine
– Matrix on PE grid1 -> Matrix on PE grid2

17. 17
API (cont..)
• Prepend LAPACK equivalent names with P.
PXYYZZZ
Computation Performed
Matrix Type
Data Types
Data Type real double cmplx dble cmplx
X S D C Z

18. 18
Matrix Types (YY) PXYYZZZ
DB General Band (diagonally dominant-like)
DT general Tridiagonal (Diagonally dominant-like)
GB General Band
GE GEneral matrices (e.g., unsymmetric, rectangular, etc.)
GG General matrices, Generalized problem
HE Complex Hermitian
OR Orthogonal Real
PB Positive definite Banded (symmetric or Hermitian)
PO Positive definite (symmetric or Hermitian)
PT Positive definite Tridiagonal (symmetric or Hermitian)
ST Symmetric Tridiagonal Real
SY SYmmetric
TR TRiangular (possibly quasi-triangular)
TZ TrapeZoidal
UN UNitary complex

19. 19
Routine types
SL Linear Equations (SVX*)
SV LU Solver
VD Singular Value
EV Eigenvalue (EVX**)
GVX Generalized Eigenvalue
*Estimates condition numbers.
*Provides Error Bounds.
*Equilibrates System.
**Selected Eigenvalues
Drivers (ZZZ) PXYYZZZ

20. 20
Rules of Thumb
• Use a square processor grid, mp=np
• Use block size 32 (Cray) or 64
– for efficient matrix multiply
• Number of PEs to use = MxN/10**6
• Bandwith/node (MB/sec) >
peak rate (MFLOPS)/10
• Latency < 500 usecs
• Use vendor’s BLAS

21. 21
Example program: Linear Equation Solution Ax=b (page 1)
ogram Sample_ScaLAPACK_program
plicit none
clude "mpif.h"
AL :: A ( 1000 , 1000)
AL, DIMENSION(:,:), ALLOCATABLE :: A_local
TEGER, PARAMETER :: M_A=1000, N_A=1000
TEGER :: DESC_A(1:9)
AL, DIMENSION(:,:), ALLOCATABLE :: b_local
AL :: b( 1000,1 )
TEGER, PARAMETER :: M_B=1000, N_B=1
TEGER :: DESC_b(1:9) ,i,j
TEGER :: ldb_y
TEGER :: ipiv(1:1000),info
TEGER :: myrow,mycol !row and column # of PE on PE grid
TEGER :: ictxt !context handle.....like MPIcommunicator
TEGER :: lda_y,lda_x ! leading dimension of local array A(@)
row and column # of PE grid
TEGER, PARAMETER :: nprow=2, npcol=2
RSRC...the PE row that owns the first row of A
CSRC...the PE column that owns the first column of A

22. 22
Example program (page 2)
INTEGER, PARAMETER :: RSRC = 0, CSRC = 0
INTEGER, PARAMETER :: MB = 32, NB=32
!
! iA...the global row index of A, which points to the beginning
!of submatrix that will be operated on.
!
INTEGER, PARAMETER :: iA = 1, jA = 1
INTEGER, PARAMETER :: iB = 1, jB = 1
REAL :: starttime, endtime
INTEGER :: taskid,numtask,ierr
!**********************************
! NOTE: ON THE NPACI MACHINES DO NOT NEED TO CALL INITBUFF
! ON OTHER MACHINES YOU MAY NEED TO CALL INITBUFF
!*************************************
!
! This is where you should define any other variables
!
INTEGER, EXTERNAL :: NUMROC
!
! Initialization of the processor grid. This routine
! must be called
!
! start MPI initialization routines

23. 23
Example program (page 3)
PI_INIT(ierr)
PI_COMM_RANK(MPI_COMM_WORLD,taskid,ierr)
PI_COMM_SIZE(MPI_COMM_WORLD,numtask,ierr)
t timing call on 0,0 processor
skid==0) THEN
ime =MPI_WTIME()
LACS_GET(0,0,ictxt)
LACS_GRIDINIT(ictxt,'r',nprow,npcol)
call returns processor grid information that will be
to distribute the global array
LACS_GRIDINFO(ictxt, nprow, npcol, myrow, mycol )
ne lda_x and lda_y with numroc
x...the leading dimension of the local array storing the
....local blocks of the distributed matrix A
= NUMROC(M_A,MB,myrow,0,nprow)
= NUMROC(N_A,NB,mycol,0,npcol)
zing A so don't waste space

24. 24
Example program (page 4)
ALLOCATE( A_local (lda_x,lda_y))
if (N_B < NB )then
ALLOCATE( b_local(lda_x,N_B) )
else
ldb_y =
NUMROC(N_B,NB,mycol,0,npcol)
ALLOCATE( b_local(lda_x,ldb_y) )
end if
!
! defining global matrix A
!
do i=1,1000
do j = 1, 1000
if (i==j) then
A(i,j) = 1000.0*i*j
else
A(i,j) = 10.0*(i+j)
end if
end do
end do
! defining the global array b
do i = 1,1000
b(i,1) = 1.0
end do
!

25. 25
Example program (page 5)
! subroutine setarray maps global array to local arrays
!
! YOU MUST HAVE DEFINED THE GLOBAL MATRIX BEFORE THIS
POINT
!
CALL SETARRAY(A,A_local,b,b_local,myrow,mycol ,
lda_x,lda_y )
!
! initialize descriptor vector for scaLAPACK
!
CALL
DESCINIT(DESC_A,M_A,N_A,MB,NB,RSRC,CSRC,ictxt,lda_x,info
)
CALL
DESCINIT(DESC_b,M_B,N_B,MB,N_B,RSRC,CSRC,ictxt,lda_x,inf
o)
!
! call scaLAPACK routines
!
CALL PSGESV( N_A,1,A_local,iA,jA,
DESC_A,ipiv,b_local,iB,jB,DESC_b,info)
!
! check ScaLAPACK returned ok
!

26. 26
Example program (page 6)
if (info .ne. 0)then
print *,'unsucessfull
return...something is wrong! info=',info
else
print *,'Sucessfull return'
end if
CALL BLACS_GRIDEXIT( ictxt )
CALL BLACS_EXIT ( 0 )
! call timing routine on processor 0,0 to
get endtime
IF (taskid==0) THEN
endtime = MPI_WTIME()
print*,'wall clock time in second =
',endtime - starttime
END IF
! end MPI
CALL MPI_FINALIZE(ierr)
!
! end of main
!
END

27. 27
Example program (page 7)
SUBROUTINE SETARRAY(AA,A,BB,B,myrow,mycol,lda_x, lda_y )
! reads in global matrix A_local and
! distributes to the local arrays.
!
implicit none
REAL :: AA(1000,1000)
REAL :: BB(1000,1)
INTEGER :: lda_x, lda_y
REAL :: A(lda_x,lda_y)
REAL ::ll,mm,Cr,Cc
INTEGER :: ii,jj,I,J,myrow,mycol,pr,pc,h,g
INTEGER , PARAMETER :: nprow = 2, npcol =2
INTEGER, PARAMETER ::N=1000,M=1000,NB=32,MB=32,RSRC=0,CSRC=0
REAL :: B(lda_x,1)
INTEGER, PARAMETER :: N_B = 1

28. 28
mple program (page 8)
1,M
o J = 1,N
! finding out which PE gets this I,J element
Cr = real( (I-1)/MB )
h = RSRC+aint(Cr)
pr = mod( h,nprow)
Cc = real( (J-1)/MB )
g = CSRC+aint(Cc)
pc = mod(g,nprow)
!
! check if on this PE and then set A
!
if (myrow ==pr .and. mycol==pc)then
! ii,jj coordinates of local array element
! ii = x + l*MB
! jj = y + m*NB
!
ll = real( ( (I-1)/(nprow*MB) ) )
mm = real( ( (J-1)/(npcol*NB) ) )
ii = mod(I-1,MB) + 1 + aint(ll)*MB
jj = mod(J-1,NB) + 1 + aint(mm)*NB
A(ii,jj) = AA(I,J)
end if
nd do
o

29. 29
mple Program (page 9)
ing in and distributing B vector
1, M
= 1
! finding out which PE gets this I,J element
Cr = real( (I-1)/MB )
h = RSRC+aint(Cr)
pr = mod( h,nprow)
Cc = real( (J-1)/MB )
g = CSRC+aint(Cc)
pc = mod(g,nprow)
! check if on this PE and then set A
if (myrow ==pr .and. mycol==pc)then
ll = real( ( (I-1)/(nprow*MB) ) )
mm = real( ( (J-1)/(npcol*NB) ) )
jj = mod(J-1,NB) + 1 + aint(mm)*NB
ii = mod(I-1,MB) + 1 + aint(ll)*MB
B(ii,jj) = BB(I,J)
end if
broutine

30. 30
1055 1070 1075
3630 4005 4258 4171 4292
13456 14287 15419 15858 16755
755
2514 2850 3040
6205 8709 9861 10468 10774
463 470
926 1031 632 1754
4130 5457 6041 6360 6647
Cray
T3E
IBM
SP2
Now
Berkeley
N= 2000 4000 6000 8000 10000
2x2
4x4
8x8
2x2
4x4
8x8
2x2
4x4
8x8
PxGEMM (mflops)

31. 31
1x4
2x8
4x16
1x4
2x8
4x16
1x4
2x8
4x16
702 884 932
1508 2680 3218 3356 3602
2419 6912 9028 10299 12547
421 603
722 1543 1903 2149
721 2084 2837 3344 3963
350
811 1310 1472 1547
1171 3091 3937 4263 4560
Cray
T3E
IBM
SP2
Now
Berkeley
N= 2000 5000 75000 10000 15000
1x4
2x8
4x16
1x4
2x8
4x16
1x4
2x8
4x16
PxGESV (mflops)