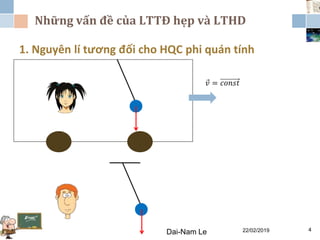
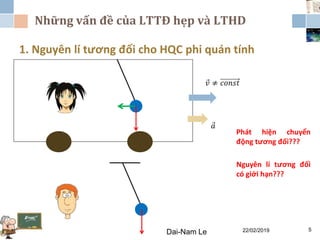
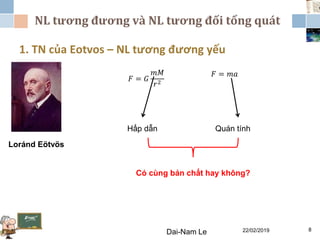
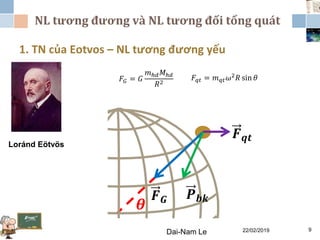
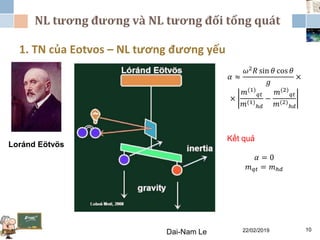
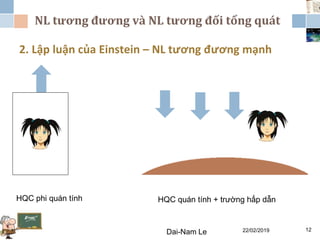
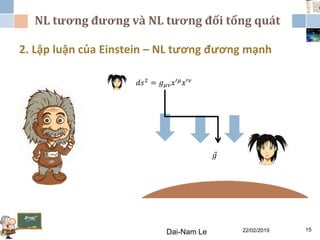
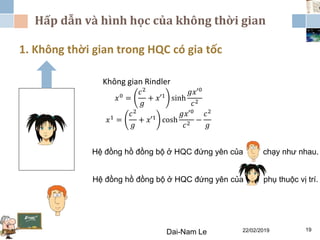
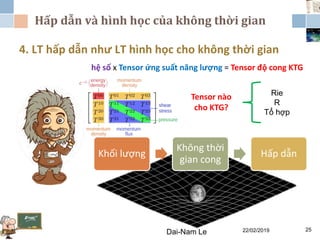
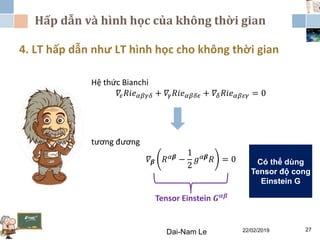
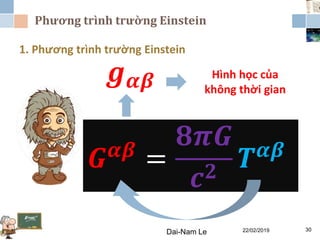
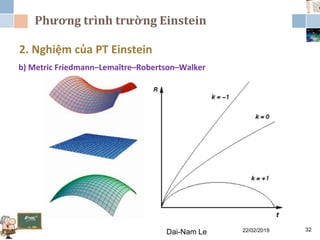
Chương 3 của lý thuyết tương đối tập trung vào lý thuyết tương đối rộng, giải thích những vấn đề của lý thuyết tương đối hẹp và hấp dẫn, cùng với các hệ quả của lý thuyết này. Nó bao gồm phương trình trường Einstein, nguyên lý tương đương và tổng quát, cùng với mối liên hệ giữa hấp dẫn và hình học không thời gian. Tài liệu cũng trình bày về các metric và nghiệm của phương trình trường Einstein, minh họa các ứng dụng trong vũ trụ học.

1. LÝ THUYẾT TƯƠNG ĐỐI
Chương 3: Lý thuyết tương đối rộng và hệ quả
22/02/2019Dai-Nam Le 1

2. NỘI DUNG
Lý
thuyết
tương
đối
rộng
và
hệ quả
Những vấn đề của Lí thuyết tương đối hẹp và Lí thuyết hấp dẫn
Những hệ quả của Lí thuyết tương đối rộng
Phương trình trường Einstein
Nguyên lí tương đương và Nguyên lí tương đối tổng quát
Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 2

3. Những vấn đề của LTTĐ hẹp và LTHD
Lý
thuyết
tương
đối
rộng
và
hệ quả
Những vấn đề của Lí thuyết tương đối hẹp và Lí thuyết hấp dẫn
Những hệ quả của Lí thuyết tương đối rộng
Phương trình trường Einstein
Nguyên lí tương đương và Nguyên lí tương đối tổng quát
Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 3

4. Những vấn đề của LTTĐ hẹp và LTHD
22/02/2019Dai-Nam Le 4
1. Nguyên lí tương đối cho HQC phi quán tính
𝑣 = 𝑐𝑜𝑛𝑠𝑡

5. Những vấn đề của LTTĐ hẹp và LTHD
22/02/2019Dai-Nam Le 5
1. Nguyên lí tương đối cho HQC phi quán tính
𝑣 ≠ 𝑐𝑜𝑛𝑠𝑡
𝑎
Phát hiện chuyển
động tương đối???
Nguyên lí tương đối
có giới hạn???

6. Những vấn đề của LTTĐ hẹp và LTHD
22/02/2019Dai-Nam Le 6
2. Trường hấp dẫn
𝑔
có phương ưu tiên
Không có phương ưu tiên Nguyên nhân gây ra hấp dẫn???
LTTĐ ntn khi tính đến hấp dẫn???

7. NL tương đương và NL tương đối tổng quát
Lý
thuyết
tương
đối
rộng
và
hệ quả
Những vấn đề của Lí thuyết tương đối hẹp và Lí thuyết hấp dẫn
Những hệ quả của Lí thuyết tương đối rộng
Phương trình trường Einstein
Nguyên lí tương đương và Nguyên lí tương đối tổng quát
Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 7

8. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 8
1. TN của Eotvos – NL tương đương yếu
Loránd Eötvös
𝐹 = 𝐺
𝑚𝑀
𝑟2
𝐹 = 𝑚𝑎
Hấp dẫn Quán tính
Có cùng bản chất hay không?

9. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 9
1. TN của Eotvos – NL tương đương yếu
Loránd Eötvös
𝐹𝐺 = 𝐺
𝑚ℎ𝑑 𝑀ℎ𝑑
𝑅2
𝐹𝑞𝑡 = 𝑚 𝑞𝑡 𝜔2 𝑅 sin 𝜃
𝜽
𝑭 𝑮
𝑭 𝒒𝒕
𝑷 𝒃𝒌

10. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 10
1. TN của Eotvos – NL tương đương yếu
Loránd Eötvös
𝛼 ≈
𝜔2 𝑅 sin 𝜃 cos 𝜃
𝑔
×
×
𝑚(1)
𝑞𝑡
𝑚(1)
ℎ𝑑
−
𝑚(2)
𝑞𝑡
𝑚(2)
ℎ𝑑
Kết quả
𝛼 = 0
𝑚 𝑞𝑡 = 𝑚ℎ𝑑

11. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 11
1. TN của Eotvos – NL tương đương yếu
𝑚 𝑞𝑡 = 𝑚ℎ𝑑
Quán tính tương đương Hấp dẫn

12. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 12
2. Lập luận của Einstein – NL tương đương mạnh
HQC phi quán tính HQC quán tính + trường hấp dẫn

13. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 13
2. Lập luận của Einstein – NL tương đương mạnh
Một HQC có gia tốc tương đương
một HQC quán tính có thêm
trường hấp dẫn (địa phương)

14. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 14
2. Lập luận của Einstein – NL tương đương mạnh
Không gian Rindler
𝑥0
=
𝑐2
𝑔
+ 𝑥′1
sinh
𝑔𝑥′0
𝑐2
𝑥1
=
𝑐2
𝑔
+ 𝑥′1
cosh
𝑔𝑥′0
𝑐2 −
𝑐2
𝑔
𝑑𝑠2
= 𝜂 𝜇𝜈 𝑥 𝜇
𝑥 𝜈
𝑑𝑠2
= 𝑔 𝜇𝜈 𝑥′ 𝜇
𝑥′ 𝜈

15. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 15
2. Lập luận của Einstein – NL tương đương mạnh
𝑑𝑠2
= 𝑔 𝜇𝜈 𝑥′ 𝜇
𝑥′ 𝜈
𝑔

16. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 16
2. Lập luận của Einstein – NL tương đương mạnh
Các PT Vật lý trong HQC PQT
 PT Vật lý + Hấp dẫn trong HQC QT
 Metric xác định (Không – thời gian xác định)

17. NL tương đương và NL tương đối tổng quát
22/02/2019Dai-Nam Le 17
3. NL tương đối tổng quát
Các định luật Vật lý như nhau trong mọi hệ quy chiếu.
(HQC PQT thì áp dụng NL tương đương)

18. Hấp dẫn và hình học của không thời gian
Lý
thuyết
tương
đối
rộng
và
hệ quả
Những vấn đề của Lí thuyết tương đối hẹp và Lí thuyết hấp dẫn
Những hệ quả của Lí thuyết tương đối rộng
Phương trình trường Einstein
Nguyên lí tương đương và Nguyên lí tương đối tổng quát
Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 18

19. Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 19
1. Không thời gian trong HQC có gia tốc
Không gian Rindler
𝑥0 =
𝑐2
𝑔
+ 𝑥′1 sinh
𝑔𝑥′0
𝑐2
𝑥1 =
𝑐2
𝑔
+ 𝑥′1 cosh
𝑔𝑥′0
𝑐2
−
𝑐2
𝑔
Hệ đồng hồ đồng bộ ở HQC đứng yên của chạy như nhau.
Hệ đồng hồ đồng bộ ở HQC đứng yên của phụ thuộc vị trí.

20. Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 20
2. Không thời gian trong HQC quay

21. Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 21
3. Thế nào là hình học phi Euclide?

22. Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 22
3. Thế nào là hình học phi Euclide?

23. Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 23
3. Thế nào là hình học phi Euclide?

24. Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 24
3. Thế nào là hình học phi Euclide?
Metric của đa tạp (𝑔 = 𝜂 nếu không gian phẳng)
𝑑𝑠2 = 𝑔 𝜇𝜈 𝑥 𝜇 𝑥 𝜈.
Vector đơn vị tiếp tuyến đường 𝑥 𝜇 = const là vector cơ sở 𝑒 𝜇.
Kí hiệu Christoffel Γ 𝜇
𝛼𝛽 của đa tạp
𝜕 𝛼 𝑒 𝛽 = Γ 𝜇
𝛼𝛽 𝑒 𝜇.
Tensor độ cong Riemann (Rie = 0 nếu không gian phẳng)
𝑅𝑖𝑒 𝜌
𝜎𝜇𝜈 = 𝜕𝜇Γ 𝜌
𝜈𝜎 − 𝜕𝜈Γ 𝜌
𝜇𝜎 + Γ 𝜌
𝜇𝜆Γ 𝜆
𝜈𝜎 − Γ 𝜌
𝜈𝜆Γ 𝜆
𝜇𝜎.
Tensor độ cong Ricci (R = 0 nếu không gian phẳng)
𝑅 𝛼𝛽 = 𝑅𝑖𝑒 𝜸
𝛼𝜸𝛽.
Vô hướng Ricci (R = 0 nếu không gian phẳng)
𝑅 = 𝑔 𝜇𝜈 𝑅 𝜇𝜈

25. Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 25
4. LT hấp dẫn như LT hình học cho không thời gian
Khối lượng
Không thời
gian cong
Hấp dẫn
Tensor nào
cho KTG?
hệ số x Tensor ứng suất năng lượng = Tensor độ cong KTG
Rie
R
Tổ hợp

26. Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 26
4. LT hấp dẫn như LT hình học cho không thời gian
BTNL cục bộ PT liên tục (4 chiều)
𝛻 𝜷 𝑇 𝛼𝜷
= 0
⟺ 𝜕 𝜷 𝑇 𝛼𝜷 + Γ 𝛼
𝜸𝜷 𝑇 𝜸𝜷 + Γ 𝜷
𝜸𝜷 𝑇 𝛼𝜸 = 0

27. Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 27
4. LT hấp dẫn như LT hình học cho không thời gian
Hệ thức Bianchi
𝛻𝜀 𝑅𝑖𝑒 𝛼𝛽𝛾𝛿 + 𝛻𝛾 𝑅𝑖𝑒 𝛼𝛽𝛿𝜀 + 𝛻𝛿 𝑅𝑖𝑒 𝛼𝛽𝜀𝛾 = 0
tương đương
𝛻 𝜷 𝑅 𝛼𝜷 −
1
2
𝑔 𝛼𝜷 𝑅 = 0
Tensor Einstein 𝑮 𝜶𝜷
Có thể dùng
Tensor độ cong
Einstein G

28. Phương trình trường Einstein
Lý
thuyết
tương
đối
rộng
và
hệ quả
Những vấn đề của Lí thuyết tương đối hẹp và Lí thuyết hấp dẫn
Những hệ quả của Lí thuyết tương đối rộng
Phương trình trường Einstein
Nguyên lí tương đương và Nguyên lí tương đối tổng quát
Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 28

29. Phương trình trường Einstein
22/02/2019Dai-Nam Le 29
1. Phương trình trường Einstein
hệ số x Tensor ứng suất năng lượng = Tensor độ cong KTG
Tensor Einstein 𝑮 𝜶𝜷
𝑮 𝜶𝜷
= 𝒌𝑻 𝜶𝜷

30. Phương trình trường Einstein
22/02/2019Dai-Nam Le 30
1. Phương trình trường Einstein
𝑮 𝜶𝜷
=
𝟖𝝅𝑮
𝒄 𝟐
𝑻 𝜶𝜷
𝒈 𝜶𝜷 Hình học của
không thời gian

31. Phương trình trường Einstein
22/02/2019Dai-Nam Le 31
2. Nghiệm của PT Einstein
a) Lời giải đối xứng cầu Schwarzschild
Đối xứng cầu trong chân không, nguồn điểm khối lượng M
𝑑𝑠2 = 1 −
𝑟𝑆𝑐ℎ𝑤
𝑟
𝑐2 𝑑𝑡2 −
1
1 −
𝑟𝑆𝑐ℎ𝑤
𝑟
𝑑𝑟2 + 𝑟2 𝑑Ω 𝑆2
Bán kính Schwarzschild 𝑟𝑆𝑐ℎ𝑤 = 2𝐺𝑀 𝑐2.
Hệ quả: bẻ cong tia sáng + hố đen
b) Metric Friedmann–Lemaître–Robertson–Walker
Mô tả vũ trụ phân bố đồng nhất, đẳng hướng. Nguồn phân bố đều 𝜌, áp suất p
𝑑𝑠2
= 𝑐2
𝑑𝑡2
− 𝑎 𝑡
1
1 − 𝑘𝑟2
𝑑𝑟2
+ 𝑟2
𝑑Ω 𝑆2

32. Phương trình trường Einstein
22/02/2019Dai-Nam Le 32
2. Nghiệm của PT Einstein
b) Metric Friedmann–Lemaître–Robertson–Walker

33. Những hệ quả của Lí thuyết tương đối rộng
Lý
thuyết
tương
đối
rộng
và
hệ quả
Những vấn đề của Lí thuyết tương đối hẹp và Lí thuyết hấp dẫn
Những hệ quả của Lí thuyết tương đối rộng
Phương trình trường Einstein
Nguyên lí tương đương và Nguyên lí tương đối tổng quát
Hấp dẫn và hình học của không thời gian
22/02/2019Dai-Nam Le 33

34. Những hệ quả của Lí thuyết tương đối rộng
22/02/2019Dai-Nam Le 34

35. Những hệ quả của Lí thuyết tương đối rộng
22/02/2019Dai-Nam Le 35

36. Những hệ quả của Lí thuyết tương đối rộng
22/02/2019Dai-Nam Le 36

37. Những hệ quả của Lí thuyết tương đối rộng
22/02/2019Dai-Nam Le 37

38. Những hệ quả của Lí thuyết tương đối rộng
22/02/2019Dai-Nam Le 38

39. Dai-Nam Le 22/02/2019 39
Thank You!