Lê Đại-Nam, profile picture
Uploaded byLê Đại-Nam
PPTX, PDF1,028 views

Lecture on Relativity theory - Chapter 2 Special Relativity

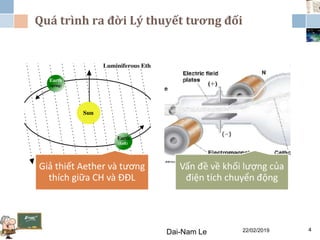
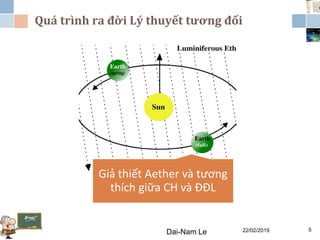
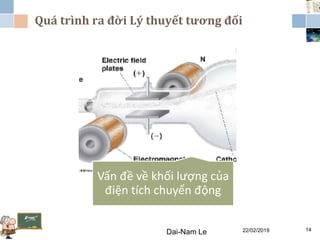
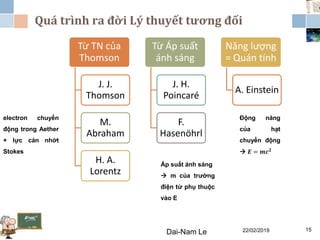
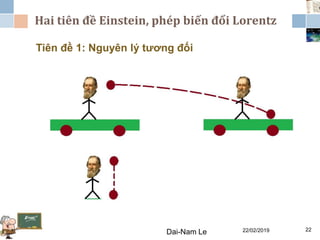
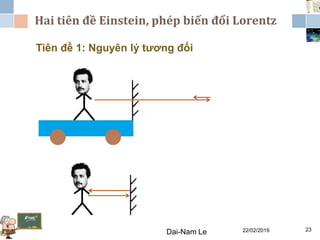
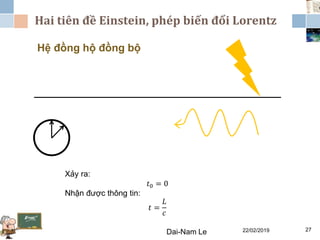
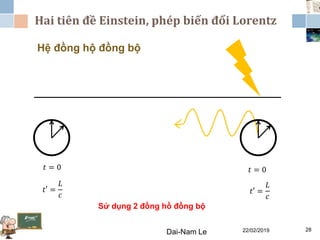
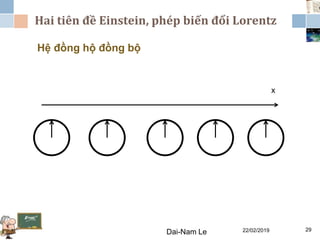
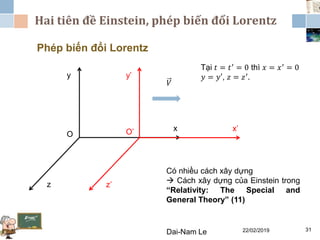
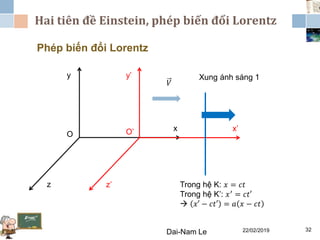
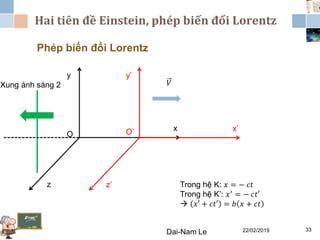
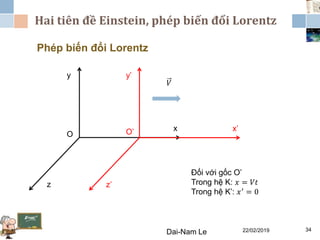
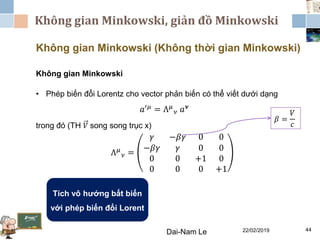
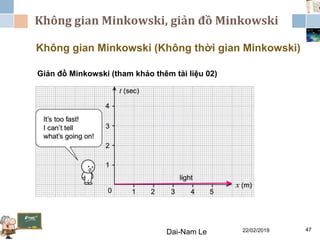
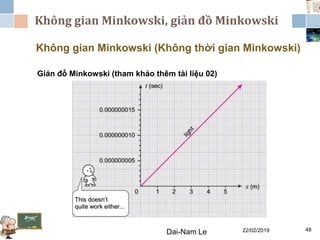
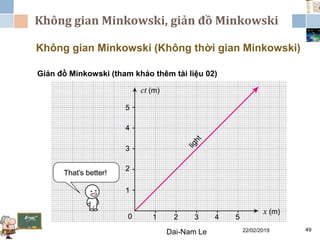
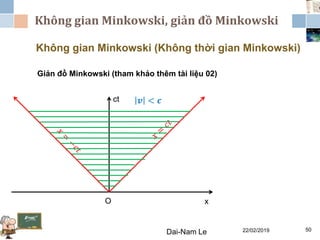
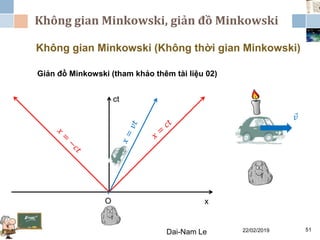
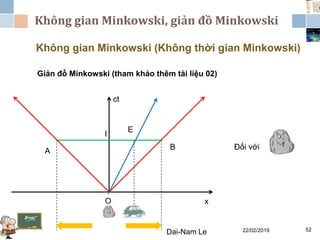
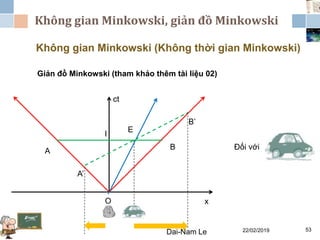
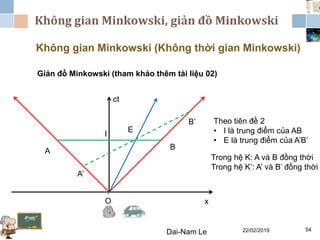
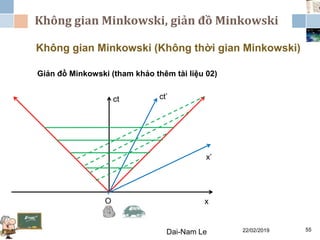
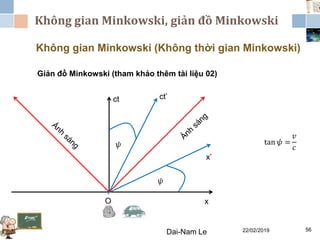
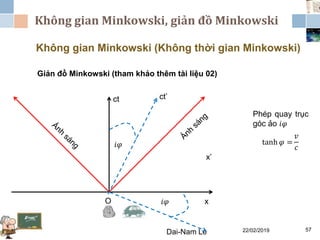
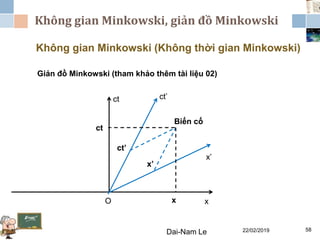
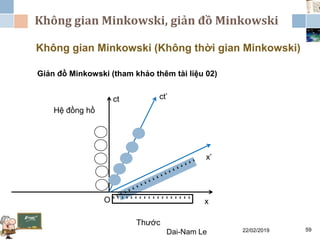
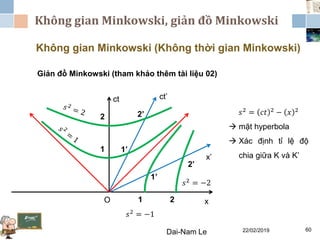
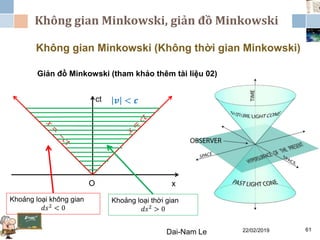
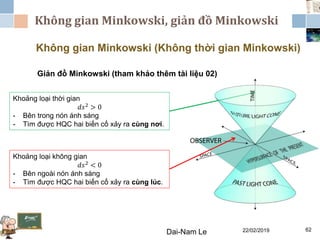
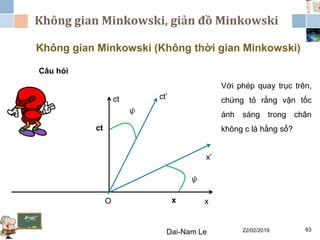
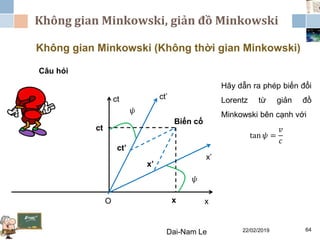
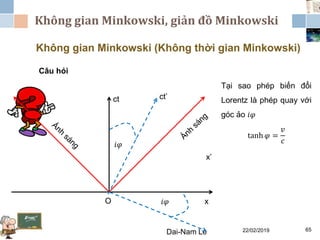
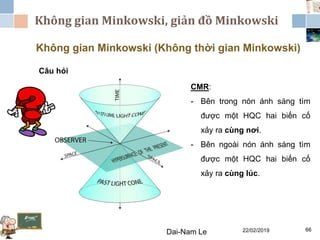
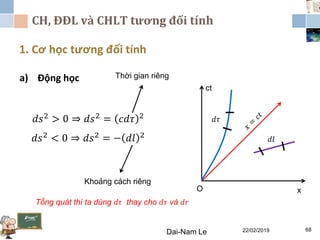
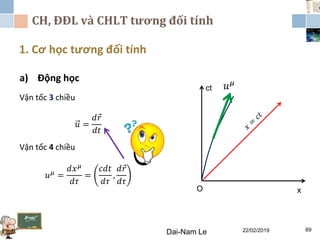
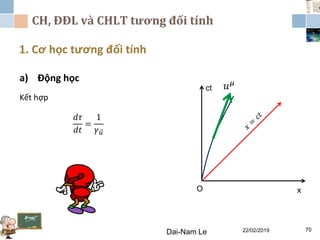
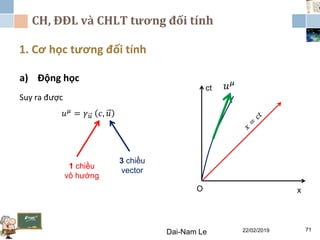
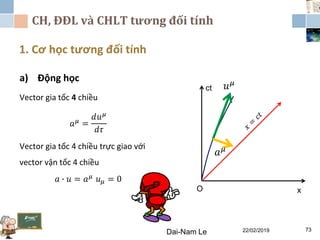
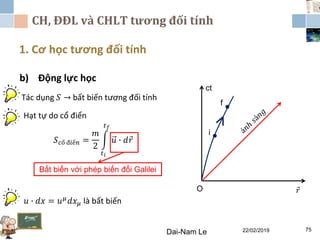
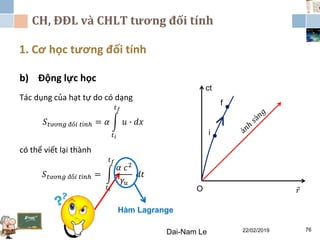
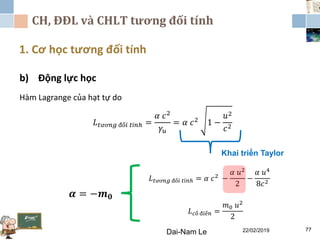
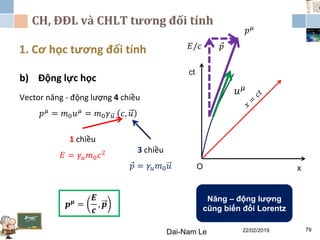
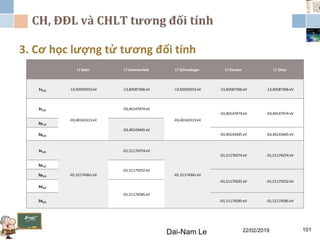
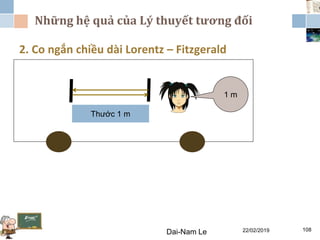
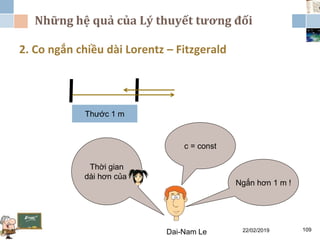
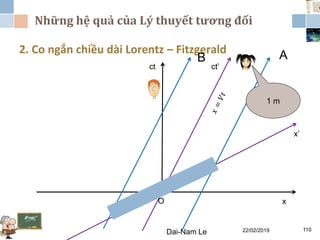
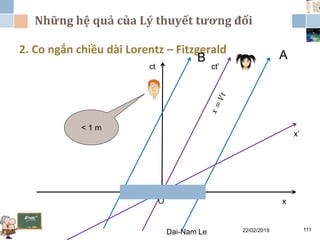
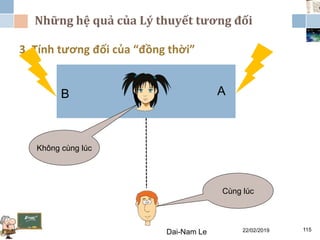
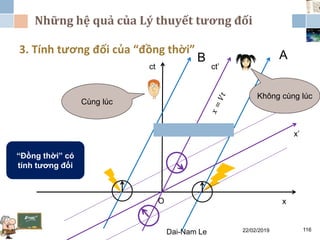
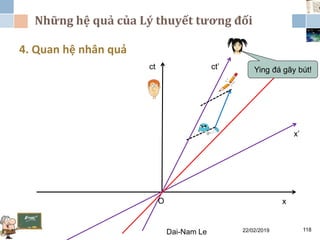
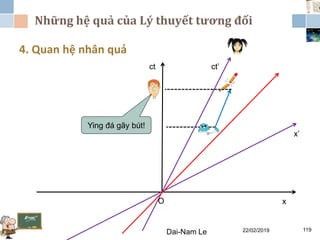
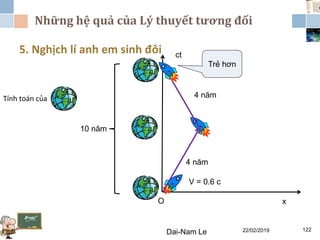
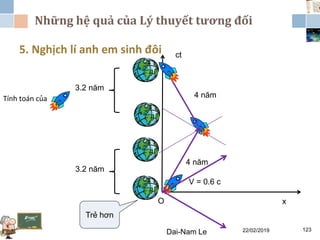
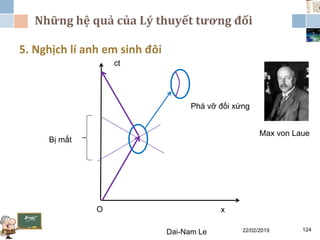
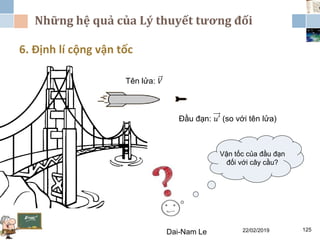
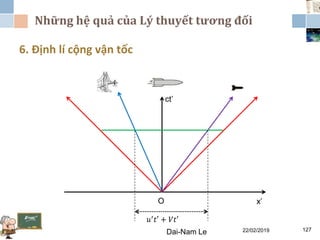
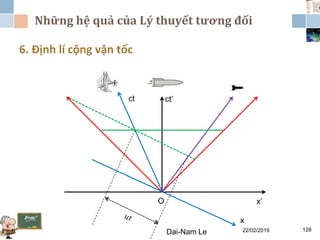
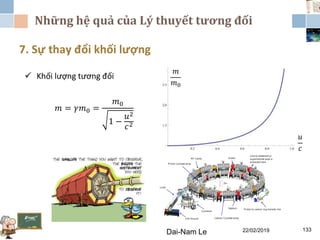
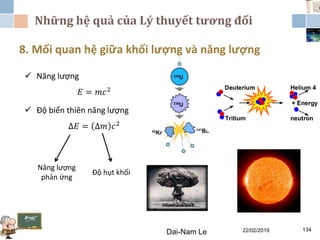
Tài liệu đề cập đến lý thuyết tương đối hẹp, bao gồm quá trình hình thành, các tiên đề của Einstein và phép biến đổi Lorentz. Nó cũng thảo luận về không gian Minkowski và những hệ quả của lý thuyết này trong cơ học, điện động lực học và cơ học lượng tử. Bài viết điểm qua các đóng góp quan trọng của các nhà khoa học như Lorentz, Poincaré và Einstein.

Embed presentation

Downloaded 18 times
1 / 142
2 / 142
3 / 142
4 / 142
Most read
5 / 142
6 / 142
7 / 142
8 / 142
Most read
9 / 142
10 / 142
11 / 142
Most read
12 / 142
13 / 142
14 / 142
15 / 142
16 / 142
17 / 142
18 / 142
19 / 142
20 / 142
21 / 142
22 / 142
23 / 142
24 / 142
25 / 142
26 / 142
27 / 142
28 / 142
29 / 142
30 / 142
31 / 142
32 / 142
33 / 142
34 / 142
35 / 142
36 / 142
37 / 142
38 / 142
39 / 142
40 / 142
41 / 142
42 / 142
43 / 142
44 / 142
45 / 142
46 / 142
47 / 142
48 / 142
49 / 142
50 / 142
51 / 142
52 / 142
53 / 142
54 / 142
55 / 142
56 / 142
57 / 142
58 / 142
59 / 142
60 / 142
61 / 142
62 / 142
63 / 142
64 / 142
65 / 142
66 / 142
67 / 142
68 / 142
69 / 142
70 / 142
71 / 142
72 / 142
73 / 142
74 / 142
75 / 142
76 / 142
77 / 142
78 / 142
79 / 142
80 / 142
81 / 142
82 / 142
83 / 142
84 / 142
85 / 142
86 / 142
87 / 142
88 / 142
89 / 142
90 / 142
91 / 142
92 / 142
93 / 142
94 / 142
95 / 142
96 / 142
97 / 142
98 / 142
99 / 142
100 / 142
101 / 142
102 / 142
103 / 142
104 / 142
105 / 142
106 / 142
107 / 142
108 / 142
109 / 142
110 / 142
111 / 142
112 / 142
113 / 142
114 / 142
115 / 142
116 / 142
117 / 142
118 / 142
119 / 142
120 / 142
121 / 142
122 / 142
123 / 142
124 / 142
125 / 142
126 / 142
127 / 142
128 / 142
129 / 142
130 / 142
131 / 142
132 / 142
133 / 142
134 / 142
135 / 142
136 / 142
137 / 142
138 / 142
139 / 142
140 / 142
141 / 142
142 / 142
LÝ THUYẾT TƯƠNG ĐỐI Chương 2: Lý thuyết tương đối hẹp và hệ quả 22/02/2019Dai-Nam Le 1
NỘI DUNG Lý thuyết tương đối và hệ quả Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 2
Quá trình ra đời Lý thuyết tương đối Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 3 Lý thuyết tương đối và hệ quả
Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 4 Giả thiết Aether và tương thích giữa CH và ĐĐL Vấn đề về khối lượng của điện tích chuyển động
Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 5 Giả thiết Aether và tương thích giữa CH và ĐĐL
22/02/2019Dai-Nam Le 6 Quá trình ra đời Lý thuyết tương đối
1907 – 1908, không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 7 Quá trình ra đời Lý thuyết tương đối 1887, xây dựng một phép biến đổi thay thế phép biến đổi Galilei cho Điện động lực . Woldemar Voigt
1907 – 1908, không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 8 Quá trình ra đời Lý thuyết tương đối Oliver Heaviside 𝑬, 𝑩 của điện tích chuyển động Joshep John Thomson Khảo sát 𝑩 gây ra bởi điện tích chuyển động trong 𝑬 Đưa ra một biểu thức tương tự co ngắn Lorentz-FitzGerald George F. C. Searle Khảo sát biến dạng của Elip Heaviside
1907 – 1908, không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 9 Quá trình ra đời Lý thuyết tương đối George Francis FitzGerald 1889, Đưa ra giả thuyết Hiệu ứng co ngắn Lorentz-FitzGerald Joseph Larmor 1897, đưa ra phép biến đổi tương tự Voigt, có một chút khác biệt. 1900, đưa ra phép biến đổi Lorentz
1907 – 1908, không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 10 Quá trình ra đời Lý thuyết tương đối 1892, đưa ra giả thuyết Hiệu ứng co ngắn Lorentz-FitzGerald. Ông cũng đưa ra một phép biến đổi mà 1897 Larmor đưa ra. Sau đó, ông đưa ra một loạt dạng phép biến đổi giữa 2 HQC quán tính. 1904, ông đưa ra được phép biến đổi Lorentz giữa 2 HQC quán tính. Áp dụng phép biến đổi Lorentz cho hệ phương trình Maxwell-Lorentz cho trường tự do. Hendrik Antoon Lorentz
1907 – 1908, không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 11 Quá trình ra đời Lý thuyết tương đối Jules Henri Poincaré 1900, khảo sát tính tương đối của khái niệm “đồng thời”. 1905, viết lại phép biến đổi Lorentz theo dạng đối xứng (hiện đại); đưa ra “nhóm Lorentz”. Áp dụng phép biến đổi Lorentz cho hệ phương trình Maxwell-Lorentz tổng quát  bước đầu phát biểu được Nguyên lý tương đối tổng quát. Bước đầu xây dựng không thời gian 4 chiều 𝒙, 𝒚, 𝒛, 𝒊𝒄𝒕
1907 – 1908, không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 12 Quá trình ra đời Lý thuyết tương đối Albert Einstein 1905, công bố bài báo Zur Elektrodynamik bewegter Körper Trong đó: • Mở rộng Nguyên lý tương đối • Công nhận c = const. • Bác bỏ giả thiết Aether • Phép biến đổi Lorentz (độc lập) • Khảo sát các hệ quả: vd biểu thức cộng vận tốc, hiệu ứng Dopler, động năng của một hạt chuyển động, …
1907 – 1908, không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 13 Quá trình ra đời Lý thuyết tương đối Hermann Minkowski 1907 – 1908, xây dựng • Không gian Minkowski + hình học của nó • Động học, Động lực học 4 chiều • Điện động lực 4 chiều Qua đó, biểu diễn lại phép biến đổi Lorentz bằng cách dùng giản đồ Minkowski
Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 14 Vấn đề về khối lượng của điện tích chuyển động
Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 15 Từ TN của Thomson J. J. Thomson M. Abraham H. A. Lorentz Từ Áp suất ánh sáng J. H. Poincaré F. Hasenöhrl Năng lượng = Quán tính A. Einstein electron chuyển động trong Aether + lực cản nhớt Stokes Áp suất ánh sáng  m của trường điện từ phụ thuộc vào E Động năng của hạt chuyển động  𝑬 = 𝒎𝒄 𝟐
Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 16 Albert Einstein Trong “Zur Elektrodynamik bewegter Körper“, Einstein đã xác định được động năng của một hạt chuyển động.  Einstein bắt đầu có những suy nghĩ về liên hệ giữa khối lượng và năng lượng  Ông tiếp tục công bố bài báo thứ hai.
Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 17 Albert Einstein Trong năm 1905, công bố bài báo “Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?“ Thông qua TN tưởng tượng, Einstein gián tiếp đồng nhất khối lượng quán tính 𝒎 với năng lượng 𝑬
Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 18 Albert Einstein
Khối lượng quán tính phải giảm xuống! Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 19 Albert Einstein ∆𝒎 = − 𝑬 𝒃ứ𝒄 𝒙ạ 𝒄 𝟐
Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 20
Hai tiên đề Einstein, phép biến đổi Lorentz Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 21 Lý thuyết tương đối và hệ quả
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 22 Tiên đề 1: Nguyên lý tương đối
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 23 Tiên đề 1: Nguyên lý tương đối
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 24 Tiên đề 1: Nguyên lý tương đối Mọi hiện tượng vật lý đều diễn ra như nhau trong mọi hệ quy chiếu quán tính. • Mở rộng Nguyên lý tương đối của Galilei cho mọi hiện tượng vật lý: bao gồm cả Cơ, Nhiệt, Điện Từ, Quang, …. • Như nhau  các PT vật lý giữ nguyên dạng  Không có HQC ưu tiên, do đó không có aether.
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 25 Tiên đề 2: Tính bất biến của vận tốc ánh sáng trong chân không Vận tốc ánh sáng trong chân không c không phụ thuộc vào chuyển động của nguồn sáng. • Trong nhiều giả thiết khác nhau, Einstein cho rằng chỉ cần sử dụng tiên đề này + Nguyên lý tương đối là đủ. • Lưu ý: trong tiên đề này chỉ đề cập đến vận tốc ánh sáng trong chân không • Hệ quả: không có vận tốc vật lý nào lớn hơn c  giả định về tachyon.
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 26 Sự kiện – Hệ quy chiếu Sự kiện được xác định bởi vị trí trong không gian (x, y, z) và thời điểm (t) 𝑥, 𝑦, 𝑧, 𝑡 Hệ quy chiếu bao gồm • Vật làm mốc • Hệ trục tọa độ + thước • Mốc thời gian + hệ đồng hồ đồng bộ
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 27 Hệ đồng hộ đồng bộ Xảy ra: 𝑡0 = 0 Nhận được thông tin: 𝑡 = 𝐿 𝑐
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 28 Hệ đồng hộ đồng bộ 𝑡 = 0𝑡 = 0 𝑡′ = 𝐿 𝑐 𝑡′ = 𝐿 𝑐 Sử dụng 2 đồng hồ đồng bộ
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 29 Hệ đồng hộ đồng bộ x
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 30 Hệ đồng hộ đồng bộ O x y z • Mỗi điểm trong không gian có một đồng hồ • Tất các các đồng hồ tạo thành một hệ đồng hồ. • Hệ đồng hồ này được đồng bộ với nhau.  Bác bỏ tính đồng thời theo cách hiểu của cơ học cổ điển.
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 31 Phép biến đổi Lorentz x y z O x’ y’ z’ O’ 𝑉 Tại 𝑡 = 𝑡′ = 0 thì 𝑥 = 𝑥′ = 0 𝑦 = 𝑦′, 𝑧 = 𝑧′. Có nhiều cách xây dựng  Cách xây dựng của Einstein trong “Relativity: The Special and General Theory” (11)
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 32 Phép biến đổi Lorentz x y z O x’ y’ z’ O’ 𝑉 Xung ánh sáng 1 Trong hệ K: 𝑥 = 𝑐𝑡 Trong hệ K’: 𝑥′ = 𝑐𝑡′  𝑥′ − 𝑐𝑡′ = 𝑎 𝑥 − 𝑐𝑡
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 33 Phép biến đổi Lorentz x y z O x’ y’ z’ O’ 𝑉Xung ánh sáng 2 Trong hệ K: 𝑥 = − 𝑐𝑡 Trong hệ K’: 𝑥′ = − 𝑐𝑡′  𝑥′ + 𝑐𝑡′ = 𝑏 𝑥 + 𝑐𝑡
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 34 Phép biến đổi Lorentz x y z O x’ y’ z’ O’ 𝑉 Đối với gốc O’ Trong hệ K: 𝑥 = 𝑉𝑡 Trong hệ K’: 𝑥′ = 0
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 35 Phép biến đổi Lorentz Tổng hợp lại, ta có 3 phương trình 𝑥′ − 𝑐𝑡′ = 𝑎 𝑥 − 𝑐𝑡 (I) 𝑥′ + 𝑐𝑡′ = 𝑏 𝑥 + 𝑐𝑡 (II) 𝑥′ = 0, 𝑥 = 𝑣𝑡 (III) Từ (I) và (II) ta giải ra 𝑥′ = 𝑎+𝑏 2 𝑥 + 𝑏−𝑎 2 𝑐𝑡 (IV) 𝑡′ = 𝑎+𝑏 2 𝑡 + 𝑏−𝑎 2𝑐 𝑥 (V) Thay (IV), (V) vào (III) 𝑎−𝑏 𝑎+𝑏 = 𝑉 𝑐 (VI) Từ (VI), ta viết lại (IV), (V) thành 𝑥′ = 𝜅 𝑥 − 𝑉𝑡 (VII) 𝑡′ = 𝜅 𝑡 − 𝑉 𝑐2 𝑥 (VIII)
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 36 Phép biến đổi Lorentz Từ phép biến đổi (VII) và (VIII), ta xây dựng phép biến đổi ngược 𝑥 = 1 𝜅 1− 𝑉2 𝑐2 𝑥′ + 𝑉𝑡′ (IX) 𝑡 = 1 𝜅 1− 𝑉2 𝑐2 𝑡′ + 𝑉 𝑐2 𝑥′ (X) Do phép biến đổi giữa K và K’ là đối xứng nên 1 𝜅 1− 𝑉2 𝑐2 = 𝜅 Hay 𝜿 = 𝟏 𝟏− 𝑽 𝟐 𝒄 𝟐 (XI)
Hai tiên đề Einstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 37 Phép biến đổi Lorentz Tổng hợp lại, ta có phép biến đổi Lorentz giữa K và K’ 𝒙′ = 𝒙−𝑽𝒕 𝟏− 𝑽 𝟐 𝒄 𝟐 𝒚′ = 𝒚 𝒛′ = 𝒛 𝒕′ = 𝒕− 𝑽 𝒄 𝟐 𝒙 𝟏− 𝑽 𝟐 𝒄 𝟐 Thừa số Lorentz 𝛾 = 1 1− 𝑉2 𝑐2
22/02/2019Dai-Nam Le 38 Câu hỏi: Hãy áp dụng phép biến đổi Lorentz để biến đổi phương trình truyền sóng điện từ trong HQC K ΔΨ = 1 𝑐2 𝜕2Ψ 𝜕𝑡2 để viết lại phương trình truyền sóng điện từ trong HQC K’. Hai tiên đề Einstein, phép biến đổi Lorentz Câu hỏi: Hãy so sánh 𝑐2 𝑡2 − 𝑥2 − 𝑦2 − 𝑧2 và 𝑐2 𝑡′2 − 𝑥′2 − 𝑦′2 − 𝑧′2
Không gian Minkowski, giản đồ Minkowski Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 39 Lý thuyết tương đối và hệ quả
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 40 Không gian Minkowski (Không thời gian Minkowski) Không gian Euclide (Không gian vector) x y z O 𝑟 = 𝑥, 𝑦, 𝑧 M (x,y,z) • Các tiên đề của KG Euclide • Các tiên đề về tích vô hướng Vector 𝑟 = 𝑥, 𝑦, 𝑧 ≡ 𝑥1, 𝑥2, 𝑥3 Tích vô hướng 𝑎 ⋅ 𝑏 = 𝑗=1 3 𝑎 𝑗 𝑏 𝑗 Khoảng các giữa hai điểm gần nhau 𝒅𝒍 𝟐 = 𝒅𝒙 𝟏 𝒅𝒙 𝟏 + 𝒅𝒙 𝟐 𝒅𝒙 𝟐+𝒅𝒙 𝟑 𝒅𝒙 𝟑
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 41 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Là một không gian chuẩn Euclide (pseudo-Euclidean space) • Mỗi vector gồm 4 thành phần: 1 vô hướng + 3 có hướng • Để thuận tiện, vector 4 chiều được chia làm hai loại  Vector phản biến: 𝑎 𝜇 (gồm 1 vô hướng + 3 (+ có hướng))  Vector hiệp biến: 𝑎 𝜇 (gồm 1 vô hướng + 3 (- có hướng))  Liên hệ giữa vector thường biến và hiệp biến 𝑎0 = 𝑎0, 𝑎1 = − 𝑎1, 𝑎2 = − 𝑎2, 𝑎3 = − 𝑎3 ⟹ 𝑎 𝜇 = 𝜈=0 3 𝜂 𝜇𝜈 𝑎 𝜈 = 𝜂 𝜇𝜈 𝑎 𝜈 Quy ước Einstein
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 42 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Minkowski metric tensor: 𝜂 𝜇𝜈 = +1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 −1 • Quy tắc nâng hạ chỉ số: khi nâng hạ chỉ số của vector (và các tensor hạng cao) thì  Thành phần ứng với chỉ số 0: không đổi dấu  Thành phần ứng với các chỉ số khác: đổi dấu.
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 43 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Tích vô hướng được trang bị 𝑎 ⋅ 𝑏 = 𝜇=0 3 𝑎 𝜇 𝑏 𝜇 = 𝑎 𝜇 𝑏 𝜇 = 𝜂 𝜇𝜈 𝑎 𝜇 𝑏 𝜈 = 𝑎0 𝑏0 − 𝑎1 𝑏1 − 𝑎2 𝑏2 − 𝑎3 𝑏3 • Norm của vector 4 chiều 𝑎 𝑎 2 = 𝑎 ⋅ 𝑎 = 𝑎 𝜇 𝑎 𝜇 = 𝜂 𝜇𝜈 𝑎 𝜇 𝑎 𝜈 = 𝑎0 𝑎0 − 𝑎1 𝑎1 − 𝑎2 𝑎2 − 𝑎3 𝑎3
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 44 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Phép biến đổi Lorentz cho vector phản biến có thể viết dưới dạng 𝑎′ 𝜇 = Λ 𝜇 𝜈 𝑎 𝝂 trong đó (TH 𝑉 song song trục x) Λ 𝜇 𝜈 = 𝛾 −𝛽𝛾 0 0 −𝛽𝛾 𝛾 0 0 0 0 +1 0 0 0 0 +1 𝛽 = 𝑉 𝑐 Tích vô hướng bất biến với phép biến đổi Lorent
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 45 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Biến cố (Sự kiện) được xác định bởi 𝒙, 𝒚, 𝒛, 𝒕 • Vector phản biến ứng với biến cố: 𝒙 𝝁 = 𝒄𝒕, + 𝒙, + 𝒚, + 𝒛 • Vector hiệp biến ứng với biến cố: 𝒙 𝝁 = 𝒄𝒕, − 𝒙, − 𝒚, − 𝒛 • Khoảng giữa hai biến cố lân cận nhau ds 𝒅𝒔 𝟐 = 𝒅𝒙 𝝁 𝒅𝒙 𝝁 = 𝜼 𝝁𝝂 𝒅𝒙 𝝁 𝒅𝒙 𝝂 Metric Minkowski (phẳng)Khoảng ds là một bất biến đối với phép biến đổi Lorentz
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 46 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski Không thời gian (1+3) chiều gồm  1 chiều thời gian ct  3 chiều không gian x, y, z
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 47 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02)
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 48 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02)
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 49 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02)
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 50 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x 𝒗 < 𝒄
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 51 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x 𝑣
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 52 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x A B E Đối với I
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 53 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x A B E Đối với A’ B’ I
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 54 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x A B E Theo tiên đề 2 • I là trung điểm của AB • E là trung điểm của A’B’ A’ B’ I Trong hệ K: A và B đồng thời Trong hệ K’: A’ và B’ đồng thời
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 55 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 56 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ 𝜓 𝜓 tan 𝜓 = 𝑣 𝑐
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 57 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ 𝑖𝜑 𝑖𝜑 tanh 𝜑 = 𝑣 𝑐 Phép quay trục góc ảo 𝑖𝜑
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 58 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ Biến cố x’ ct’ x ct
‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 59 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ Thước Hệ đồng hồ
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 60 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ 1 1’ 1 1’ 2 2 2’ 2’ 𝑠2 = 𝑐𝑡 2 − 𝑥 2  mặt hyperbola  Xác định tỉ lệ độ chia giữa K và K’ 𝑠2 = −1 𝑠2 = −2
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 61 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x 𝒗 < 𝒄 Khoảng loại thời gian 𝑑𝑠2 > 0 Khoảng loại không gian 𝑑𝑠2 < 0
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 62 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) Khoảng loại thời gian 𝑑𝑠2 > 0 - Bên trong nón ánh sáng - Tìm được HQC hai biến cố xảy ra cùng nơi. Khoảng loại không gian 𝑑𝑠2 < 0 - Bên ngoài nón ánh sáng - Tìm được HQC hai biến cố xảy ra cùng lúc.
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 63 Không gian Minkowski (Không thời gian Minkowski) Câu hỏi ct O x ct’ x’ x ct Với phép quay trục trên, chứng tỏ rằng vận tốc ánh sáng trong chân không c là hằng số? 𝜓 𝜓
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 64 Không gian Minkowski (Không thời gian Minkowski) Câu hỏi ct O x ct’ x’ Biến cố x’ ct’ x ct Hãy dẫn ra phép biến đổi Lorentz từ giản đồ Minkowski bên cạnh với tan 𝜓 = 𝑣 𝑐 𝜓 𝜓
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 65 Không gian Minkowski (Không thời gian Minkowski) Câu hỏi Tại sao phép biến đổi Lorentz là phép quay với góc ảo 𝑖𝜑 tanh 𝜑 = 𝑣 𝑐 ct O x ct’ x’ 𝑖𝜑 𝑖𝜑
Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 66 Không gian Minkowski (Không thời gian Minkowski) Câu hỏi CMR: - Bên trong nón ánh sáng tìm được một HQC hai biến cố xảy ra cùng nơi. - Bên ngoài nón ánh sáng tìm được một HQC hai biến cố xảy ra cùng lúc.
CH, ĐĐL và CHLT tương đối tính Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 67 Lý thuyết tương đối và hệ quả
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 68 a) Động học 𝑑𝑠2 > 0 ⇒ 𝑑𝑠2 = 𝑐𝑑𝜏 2 𝑑𝑠2 < 0 ⇒ 𝑑𝑠2 = − 𝑑𝑙 2 Thời gian riêng Khoảng cách riêng ct O x 𝑑𝜏 𝑑𝑙 Tổng quát thì ta dùng 𝑑𝜏 thay cho 𝑑𝜏 và 𝑑𝑟
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 69 a) Động học Vận tốc 3 chiều 𝑢 = 𝑑 𝑟 𝑑𝑡 Vận tốc 4 chiều 𝑢 𝜇 = 𝑑𝑥 𝜇 𝑑𝜏 = 𝑐𝑑𝑡 𝑑𝜏 , 𝑑 𝑟 𝑑𝜏 ct O x 𝑢 𝜇
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 70 a) Động học Kết hợp 𝑑𝜏 𝑑𝑡 = 1 𝛾 𝑢 ct O x 𝑢 𝜇
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 71 a) Động học Suy ra được 𝑢 𝜇 = 𝛾 𝑢 𝑐, 𝑢 ct O x 𝑢 𝜇 3 chiều vector 1 chiều vô hướng
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 72 1. Hãy xác định phép biến đổi Lorentz cho vector vận tốc 4 chiều. 2. Chứng minh rằng norm của vector vận tốc 4 chiều 𝑢 = 𝑢 𝜇 𝑢 𝜇 là một bất biến tương đối tính. Câu hỏi
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 73 a) Động học Vector gia tốc 4 chiều 𝑎 𝜇 = 𝑑𝑢 𝜇 𝑑𝜏 Vector gia tốc 4 chiều trực giao với vector vận tốc 4 chiều 𝑎 ∙ 𝑢 = 𝑎 𝜇 𝑢 𝜇 = 0 ct O x 𝑢 𝜇 𝑎 𝜇
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 74 b) Động lực học Đi từ định luật 2 Newton Xây dựng động lượng 4 chiều Đi từ nguyên lý tác dụng tối thiểu Xây dựng hàm tác dụng cho hạt tự do
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 75 b) Động lực học Tác dụng 𝑆 → bất biến tương đối tính Hạt tự do cổ điển 𝑆 𝑐ổ đ𝑖ể𝑛 = 𝑚 2 𝑡 𝑖 𝑡 𝑓 𝑢 ∙ 𝑑 𝑟 𝑢 ∙ 𝑑𝑥 = 𝑢 𝜇 𝑑𝑥 𝜇 là bất biến ct O 𝑟 i f Bất biến với phép biến đổi Galilei
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 76 b) Động lực học Tác dụng của hạt tự do có dạng 𝑆 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = 𝛼 𝑡 𝑖 𝑡 𝑓 𝑢 ∙ 𝑑𝑥 có thể viết lại thành 𝑆 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = 𝑡 𝑖 𝑡 𝑓 𝛼 𝑐2 𝛾𝑢 𝑑𝑡 ct O 𝑟 i f Hàm Lagrange
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 77 b) Động lực học Hàm Lagrange của hạt tự do 𝐿 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = 𝛼 𝑐2 𝛾𝑢 = 𝛼 𝑐2 1 − 𝑢2 𝑐2 Khai triển Taylor 𝐿 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = 𝛼 𝑐2 − 𝛼 𝑢2 2 − 𝛼 𝑢4 8𝑐2 𝐿 𝑐ổ đ𝑖ể𝑛 = 𝑚0 𝑢2 2 𝜶 = −𝒎 𝟎
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 78 b) Động lực học Vậy, hàm Lagrange của hạt tự do 𝐿 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = − 𝑚0 𝑐2 1 − 𝑢2 𝑐2  động lượng và năng lượng của hạt tự do 𝑝 = 𝛾𝑢 𝑚0 𝑢 𝐸 = 𝛾𝑢 𝑚0 𝑐2 Khối lượng tương đối
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 79 b) Động lực học Vector năng - động lượng 4 chiều 𝑝 𝜇 = 𝑚0 𝑢 𝜇 = 𝑚0 𝛾 𝑢 𝑐, 𝑢 𝒑 𝝁 = 𝑬 𝒄 , 𝒑 ct O x 𝑢 𝜇 3 chiều 𝑝 = 𝛾𝑢 𝑚0 𝑢 1 chiều 𝐸 = 𝛾𝑢 𝑚0 𝑐2 Năng – động lượng cũng biến đổi Lorentz 𝑝 𝜇 𝐸/𝑐 𝑝
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 80 b) Động lực học Định luật II Newton tương đối tính (từ Pt Euler-Lagrange) 𝐹 = 𝑑 𝑝 𝑑𝑡 = 𝑑 𝛾𝑢 𝑚0 𝑢 𝑑𝑡 Định lí động năng 𝐹 ∙ 𝑢 = 𝑑𝐸 𝑑𝑡 = 𝑑 𝛾𝑢 𝑚0 𝑐2 𝑑𝑡
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 81 b) Động lực học Đưa 𝑝 𝜇 = 𝑚0 𝑢 𝜇 = 𝐸 𝑐 , 𝑝 vào, ta có định luật II Newton 4 chiều 𝐹 𝜇 = 𝑑𝑝 𝜇 𝑑𝜏 Khái niệm lực 4 chiều 𝐹 𝜇 = 𝛾𝑢 𝐹 ∙ 𝑢 𝑐 , 𝐹 Lực cũng biến đổi Lorentz
CH, ĐĐL và CHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 82 b) Động lực học Định luật bảo toàn năng – động lượng 4 chiều 𝐹 𝜇 = 0 ⟹ 𝑑𝑝 𝜇 𝑑𝜏 = 0 Do đó 𝑑𝐸 𝑑𝑡 = 0 và 𝑑 𝑝 𝑑𝑡 = 0 Áp dụng cho bài toán va chạm
CH, ĐĐL và CHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 83 + 𝐸
CH, ĐĐL và CHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 84 + 𝐸′ 𝑡 − 𝑟 𝑐 𝑟 = 𝑐𝑡 𝐼 𝐵′ 𝑡𝐸 → 𝐸′, 𝐵′
CH, ĐĐL và CHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 85 + 𝐵 + + ++ + + + + - - - -- - - - -
CH, ĐĐL và CHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 86 𝐵′ + - - - -- - - - - ++ ++ +++ + 𝐸′ 𝐵 → 𝐸′, 𝐵′
CH, ĐĐL và CHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 87 Điện trường và từ trường cũng biến đổi (Lorentz) Xét trường hợp trường điện từ tự do trong HQC K 𝛻 ∙ 𝐸 = 0 𝛻 ∙ 𝐵 = 0 𝛻 × 𝐸 = − 𝜕𝐵 𝜕𝑡 𝛻 × 𝐵 = 1 𝑐2 𝜕𝐸 𝜕𝑡 và HQC K’ 𝛻′ ∙ 𝐸′ = 0 𝛻′ ∙ 𝐵′ = 0 𝛻′ × 𝐸′ = − 𝜕𝐵′ 𝜕𝑡′ 𝛻′ × 𝐵′ = 1 𝑐2 𝜕𝐸′ 𝜕𝑡′
CH, ĐĐL và CHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 88 Đồng nhất hai PT, ta được phép biến đổi cho các vector cường độ (tham khảo tài liệu 10) 𝐸′ 𝑥 = 𝐸 𝑥 𝐸′ 𝑦 = 𝛾 𝐸 𝑦 − 𝑉𝐵𝑧 𝐸′ 𝑧 = 𝛾 𝐸𝑧 + 𝑉𝐵𝑦 𝐵′ 𝑥 = 𝐵𝑥 𝐵′ 𝑦 = 𝛾 𝐵𝑦 + 𝑉 𝑐2 𝐸𝑧 𝐵′ 𝑧 = 𝛾 𝐵𝑧 − 𝑉 𝑐2 𝐸 𝑦 Tương tự, ta cũng có thể dẫn ra phép biến đổi cho các vector cảm ứng 𝐷′ 𝑥 = 𝐷 𝑥 𝐷′ 𝑦 = 𝛾 𝐷 𝑦 − 𝑉 𝑐2 𝐻𝑧 𝐷′ 𝑧 = 𝛾 𝐷𝑧 + 𝑉 𝑐2 𝐻 𝑦 𝐻′ 𝑥 = 𝐻 𝑥 𝐻′ 𝑦 = 𝛾 𝐻 𝑦 + 𝑉𝐷𝑧 𝐻′ 𝑧 = 𝛾 𝐻𝑧 − 𝑉𝐷 𝑦
CH, ĐĐL và CHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 89 Khi có nguồn (mật độ điện tích và mật độ dòng) thì phép biến đổi Lorentz của các đại lượng nguồn là 𝑗′ 𝑥 = 𝛾 𝑗 𝑥 − 𝜌𝑉 𝑗′ 𝑦 = 𝑗 𝑦 𝑗′ 𝑧 = 𝑗′ 𝑧 𝜌′ = 𝛾 𝜌 − 𝑉𝑗 𝑥 𝑐2 Vector mật độ dòng 4 chiều 𝑗 𝜇 = 𝑐𝜌, 𝑗 Có thể viết dưới dạng vector 4 chiều
CH, ĐĐL và CHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 90 Đối với các vector cường độ (cảm ứng): ta có 2 vector  6 thành phần ” Không viết dưới dạng vector 4 chiều được ” Tensor 4 chiều hạng 2, có 42 = 𝟏𝟔 thành phần ” Ta có 6 thành phần độc lập nên phải là tensor phản xứng ! Tensor cường độ trường điện từ 𝐹 𝜇𝜈 = 0 − 𝐸𝑥 𝑐 − 𝐸 𝑦 𝑐 −𝐸𝑧 𝑐 𝐸𝑥 𝑐 0 −𝐵𝑧 𝐵𝑦 𝐸 𝑦 𝑐 𝐵𝑧 0 −𝐵𝑥 𝐸𝑧 𝑐 −𝐵𝑦 𝐵𝑥 0
CH, ĐĐL và CHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 91 Phép biến đổi Lorentz của tensor cường độ trường điện từ 𝐹′ 𝛼𝛽 = 𝛬 𝛼 𝜇 𝛬 𝛽 𝜈 𝐹 𝜇𝜈 Chứng minh rằng 𝐹 𝜇𝜈 𝐹𝜇𝜈 = 2 𝐵2 − 1 𝑐2 𝐸2 là một bất biến tương đối tính.
CH, ĐĐL và CHLT tương đối tính 22/02/2019Dai-Nam Le 92 2. Điện động lực học tương đối tính Hiệu ứng Dopler tương đối tính Áp dụng phép biến đổi Lorentz của trường điện từ cho trường hợp của sóng điện từ, ta chứng minh được 𝑘 𝜇 = 𝑐𝜔, 𝑘 là một vector 4 chiều. Từ phép biến đổi Lorentz của 𝑘 𝜇, ta có 𝑓 𝑀 1 − 𝑣 𝑀 2 𝑐2 1 − 𝑣 𝑀 𝑐 cos 𝜃 𝐶𝑀 = 𝑓𝑆 1 − 𝑣 𝑆 2 𝑐2 1 − 𝑣 𝑆 𝑐 cos 𝜃 𝐶𝑆
CH, ĐĐL và CHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 93 Cơ học lượng tử phi tương đối tính  PT Schroedinger 𝐸 = 𝑇 + 𝑈 = 𝑝2 2𝑚 + 𝑈 Thay 𝐸 → +𝑖ℏ 𝜕 𝜕𝑡 𝑝 → −𝑖ℏ𝛻 Ta được PT Schroedinger 𝑖ℏ 𝜕 𝜕𝑡 Ψ = − ℏ2 2𝑚 𝛻2 Ψ + 𝑈Ψ
CH, ĐĐL và CHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 94 Cơ học lượng tử tương đối tính  PT Klein – Gordon 𝐸 = 𝑝2 𝑐2 + 𝑚2 𝑐4 + 𝑈 Thay 𝐸 → +𝑖ℏ 𝜕 𝜕𝑡 𝑝 → −𝑖ℏ𝛻 Ta được PT Klein – Gordon 𝑖ℏ 𝜕 𝜕𝑡 − 𝑈 2 Ψ = −ℏ2 𝑐2 𝛻2 Ψ + 𝑚2 𝑐4Ψ PT này tồn tại nhiều vấn đề nên không phải là mở rộng PT Schroedinger trong giới hạn tương đối tính cho 1 hạt. PT này sử dụng để mô tả 1 hệ hạt spin nguyên (boson)
CH, ĐĐL và CHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 95 Áp dụng PT Klein – Gordon cho hạt tự do □Ψ = 𝑚2 𝑐2 ℏ2 Ψ Thế Yukawa trong tương tác giữa nucleon – nucleon 𝑈 𝑌𝑢𝑘𝑎𝑤𝑎~ 𝑒−𝜆𝑟 𝑟 là nghiệm của PT □𝑈 𝑌𝑢𝑘𝑎𝑤𝑎 = λ2 𝑈 𝑌𝑢𝑘𝑎𝑤𝑎 Dự đoán 𝑚𝑐 ℏ = 𝜆~ 1 𝑅0 ⟹ 𝑚 = ℏ 𝑅0 𝑐 ~200 ÷ 300 𝑚 𝑒
CH, ĐĐL và CHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 96 Cơ học lượng tử tương đối tính  PT Dirac 𝑝 𝜇 𝑝 𝜇 = 𝑚2 𝑐4 Thay 𝑝 𝜇 → 𝛼1 𝜕 𝑥 + 𝛼2 𝜕 𝑦 + 𝛼3 𝜕𝑧 + 𝛽𝜕𝑡 Các “hệ số” 𝛼1, 𝛼2, 𝛼3, 𝛽 phải là các ma trận vuông 4 chiều ” Hàm sóng lưỡng spinor PT cho cơ học lượng tử tương đối tính phải là PT Dirac 𝛾 𝜇 𝑖ℏ𝜕𝜇 − 𝑒 𝑐 𝐴 𝜇 Ψ = 𝑚𝑐Ψ
CH, ĐĐL và CHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 97
CH, ĐĐL và CHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 98 PT Pauli
CH, ĐĐL và CHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 99 𝛼 = 𝑒2 4𝜋𝜀0ℏ𝑐
CH, ĐĐL và CHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 100 giải gần đúng PT Dirac Walter Gordon giải chính xác PT Dirac
CH, ĐĐL và CHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 101 LT Bohr LT Sommerfeld LT Schrodinger LT Darwin LT Dirac 1s1/2 -13,60569253 eV -13,60587366 eV -13,60569253 eV -13,60587366 eV -13,60587366 eV 2s1/2 -03,40142313 eV -03,40147974 eV -03,40142313 eV -03,40147974 eV -03,40147974 eV 2p1/2 -03,40143445 eV 2p3/2 -03,40143445 eV -03,40143445 eV 3s1/2 -01,51174361 eV -01,51176374 eV -01,51174361 eV -01,51176374 eV -01,51176374 eV 3p1/2 -01,51175032 eV 3p3/2 -01,51175032 eV -01,51175032 eV 3d3/2 -01,51174585 eV 3d5/2 -01,51174585 eV -01,51174585 eV
Những hệ quả của Lý thuyết tương đối Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 102 Lý thuyết tương đối và hệ quả
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 103 1. Giãn nở thời gian 1 s 1 s
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 104 1. Giãn nở thời gian
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 105 1. Giãn nở thời gian > 1 s 1 s
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 106 1. Giãn nở thời gian Theo định nghĩa thời gian riêng 𝑐𝑑𝜏 2 = 𝑐𝑑𝑡 2 − 𝑑𝑟 2 < 𝑐𝑑𝑡 2 ⇒ 𝑑𝑡 > 𝑑𝜏 Giãn nở thời gian Ở phần động học, ta đã có 𝑑𝜏 𝑑𝑡 = 1 𝛾 𝑢 ⟹ Δ𝑡 = 𝛾 Δ𝜏
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 107 2. Co ngắn chiều dài Lorentz – Fitzgerald Thước 1 m
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 108 2. Co ngắn chiều dài Lorentz – Fitzgerald Thước 1 m 1 m
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 109 2. Co ngắn chiều dài Lorentz – Fitzgerald Thước 1 m Thời gian dài hơn của c = const Ngắn hơn 1 m !
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 110 2. Co ngắn chiều dài Lorentz – Fitzgerald ct O x AB x’ ct’ 1 m
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 111 2. Co ngắn chiều dài Lorentz – Fitzgerald ct O x AB x’ ct’ < 1 m
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 112 2. Co ngắn chiều dài Lorentz – Fitzgerald Theo định nghĩa của chiều dài riêng − 𝑑𝑙 2 = 𝑐𝑑𝑡 2 − 𝑑𝑟 2 ⇒ 𝑑𝑙 < 𝑑𝑟 Þ co ngắn chiều dài Từ phép biến đổi Lorentz, ta có 𝑑𝑙 = 𝛾 𝑥 + 𝑑𝑟 − 𝑥 = 𝛾𝑑𝑟 ⟹ 𝑑𝑟 = 𝑑𝑙 𝛾
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 113 2. Co ngắn chiều dài Lorentz – Fitzgerald Mọi người nhìn Mr. Tompkin Mr. Tompkin nhìn mọi người
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 114 3. Tính tương đối của “đồng thời”
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 115 3. Tính tương đối của “đồng thời” Cùng lúc Không cùng lúc AB
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 116 3. Tính tương đối của “đồng thời” ct O x AB x’ ct’ Cùng lúc Không cùng lúc “Đồng thời” có tính tương đối
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 117 4. Quan hệ nhân quả Ying đá gãy bút! Ying đá ? Bút gãy ?
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 118 4. Quan hệ nhân quả ct O x x’ ct’ Ying đá gãy bút!
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 119 4. Quan hệ nhân quả ct O x x’ ct’ Ying đá gãy bút!
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 120 4. Quan hệ nhân quả Nguyên nhân  Kết quả : thông tin được truyền với vận tốc 𝑢 < 𝑐 ∆𝑡 = ∆𝑥 𝑢 ∆𝑡′ = 𝛾 ∆𝑡 − 𝑉 𝑐2 ∆𝑥 = 𝛾 1 − 𝑉𝑢 𝑐2 ∆𝑡 ⟹ ∆𝑡′ 𝑣à ∆𝑡 𝑐ù𝑛𝑔 𝑑ấ𝑢 Tính nhân quả như nhau trong mọi hệ quy chiếu quán tính.
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 121 5. Nghịch lí anh em sinh đôi Paul Langevin
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 122 5. Nghịch lí anh em sinh đôi ct O x Tính toán của 10 năm V = 0.6 c 4 năm 4 năm Trẻ hơn
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 123 5. Nghịch lí anh em sinh đôi ct O x Tính toán của 3.2 năm V = 0.6 c 4 năm 4 năm 3.2 năm Trẻ hơn
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 124 5. Nghịch lí anh em sinh đôi Max von Laue ct O x Bị mất Phá vỡ đối xứng
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 125 6. Định lí cộng vận tốc Tên lửa: 𝑉 Đầu đạn: 𝑢′ (so với tên lửa) Vận tốc của đầu đạn đối với cây cầu?
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 126 6. Định lí cộng vận tốc 𝒖 = 𝒖′ + 𝑽 Liệu nó còn đúng???
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 127 6. Định lí cộng vận tốc ct’ O x’ 𝑢′ 𝑡′ + 𝑉𝑡′
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 128 6. Định lí cộng vận tốc ct’ O x’ ct x
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 129 8. Định lí cộng vận tốc 𝒖 ≠ 𝒖′ + 𝑽  Từ phép biến đổi Lorentz của 𝑐𝑡, 𝑥, 𝑦, 𝑧 → 𝑐𝑡′, 𝑥′, 𝑦′, 𝑧′ Kết hợp 𝑢 = 𝑑 𝑟 𝑑𝑡 𝑣à 𝑢′ = 𝑑𝑟′ 𝑑𝑡  Từ phép biến đổi Lorentz của 𝑢 𝜇 → 𝑢′ 𝜇
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 130 8. Định lí cộng vận tốc 𝒖 ≠ 𝒖′ + 𝑽  Ta có định lí cộng vận tốc 𝑢1 = 𝑢′1 + 𝑉 1 + 𝑢′1 𝑉 𝑐 2 𝑢2 = 𝑢′2 𝛾 1 + 𝑢′1 𝑉 𝑐 2 𝑢3 = 𝑢′3 𝛾 1 + 𝑢′1 𝑉 𝑐 2
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 131 8. Định lí cộng vận tốc Chứng minh định lí cộng vận tốc 𝑢1 = 𝑢′1 + 𝑉 1 + 𝑢′1 𝑉 𝑐 2 𝑢2 = 𝑢′2 𝛾 1 + 𝑢′1 𝑉 𝑐 2 𝑢3 = 𝑢′3 𝛾 1 + 𝑢′1 𝑉 𝑐 2 bằng cả hai cách.
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 132 8. Định lí cộng vận tốc Sử dụng định lí cộng vận tốc để  Giải thích thí nghiệm của Fizeau về vận tốc ánh sáng trong chất lỏng chuyển động 𝑢 = 𝑐 𝑛 + 1 − 1 𝑛2 𝑣  Xây dụng công thức quang sai cho ánh sáng tan 𝜃 = sin 𝜃′ 𝛾 cos 𝜃′ + 𝑉 𝑐
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 133 7. Sự thay đổi khối lượng  Khối lượng tương đối 𝑚 = 𝛾𝑚0 = 𝑚0 1 − 𝑢2 𝑐2 𝑢 𝑐 𝑚 𝑚0
Những hệ quả của Lý thuyết tương đối 22/02/2019Dai-Nam Le 134 8. Mối quan hệ giữa khối lượng và năng lượng  Năng lượng 𝐸 = 𝑚𝑐2  Độ biến thiên năng lượng ∆𝐸 = ∆𝑚 𝑐2 Độ hụt khối Năng lượng phản ứng
Dai-Nam Le 22/02/2019 135 Thank You!
Cấu trúc đề thi giữa kì 22/02/2019Dai-Nam Le 136 Điểm giữa kì chiếm 20% Đề thi gồm 04 câu bài tập 1. Lí thuyết cổ điển + tương đối 4 điểm 2. Phép biến đổi Lorentz và hệ quả 3 điểm 3. Động học tương đối tính 2 điểm 4. Câu hỏi phân loại 1 điểm
Tìm hiểu thêm 22/02/2019Dai-Nam Le 137 Bài toán phân rã và va chạm Rã 2 hạt 𝐴 → 𝐵 + 𝐶 HQC phòng thí nghiệm A B C
Tìm hiểu thêm 22/02/2019Dai-Nam Le 138 Bài toán phân rã và va chạm Rã 2 hạt 𝐴 → 𝐵 + 𝐶 HQC khối tâm A B C
𝐴 → 𝐵 + 𝐶 VD: 𝜋0 → 𝛾 + 𝛾 (𝑏𝑟𝑎𝑛𝑐ℎ𝑖𝑛𝑔 𝑟𝑎𝑡𝑖𝑜 = 0.98823) Tìm hiểu thêm 22/02/2019Dai-Nam Le 139 Bài toán phân rã và va chạm Rã 2 hạt
VD: 𝜋0 → 𝛾 + 𝛾 (𝑏𝑟𝑎𝑛𝑐ℎ𝑖𝑛𝑔 𝑟𝑎𝑡𝑖𝑜 = 0.98823) Tìm hiểu thêm 22/02/2019Dai-Nam Le 140 Bài toán phân rã và va chạm Rã 2 hạt
Tìm hiểu thêm 22/02/2019Dai-Nam Le 141 Bài toán trường xuyên tâm trong Lí thuyết tương đối
Tìm hiểu thêm 22/02/2019Dai-Nam Le 142 Giới hạn ứng dụng của Lí thuyết tương đối

More Related Content

PDF
Lecture note on Theory of Solid state Physics
byLê Đại-Nam
 
PDF
Homework: Structure of atoms and molecules (Ph.D. course)
byLê Đại-Nam
 
DOC
Tiểu luận Vai trò của tri thức khoa học công nghệ đối với việc phát triển kin...
byViết Thuê Luận Văn Luanvanpanda.com
 
PDF
KẾ HOẠCH DẠY HỌC CỦA TỔ CHUYÊN MÔN. MÔN HỌC VẬT LÝ- CÔNG NGHỆ.pdf
byjackjohn45
 
PDF
Giáo trình điện động lực học
bywww. mientayvn.com
 
PDF
KHÓA LUẬN TỐT NGHIỆP CÁC PHƯƠNG PHÁP GIẢI TÍCH GIẢI BÀI TOÁN PHƯƠNG TRÌNH VẬT...
bynataliej4
 
PDF
Nganhang trac nghiem ly co dap an
byXuan Quyet Cecil
 
PDF
Rèn luyện kỹ năng giải toán phương trình lượng giác cho học sinh lớp 11 trung...
byjackjohn45
 
Lecture note on Theory of Solid state Physics
byLê Đại-Nam
 
Homework: Structure of atoms and molecules (Ph.D. course)
byLê Đại-Nam
 
Tiểu luận Vai trò của tri thức khoa học công nghệ đối với việc phát triển kin...
byViết Thuê Luận Văn Luanvanpanda.com
 
KẾ HOẠCH DẠY HỌC CỦA TỔ CHUYÊN MÔN. MÔN HỌC VẬT LÝ- CÔNG NGHỆ.pdf
byjackjohn45
 
Giáo trình điện động lực học
bywww. mientayvn.com
 
KHÓA LUẬN TỐT NGHIỆP CÁC PHƯƠNG PHÁP GIẢI TÍCH GIẢI BÀI TOÁN PHƯƠNG TRÌNH VẬT...
bynataliej4
 
Nganhang trac nghiem ly co dap an
byXuan Quyet Cecil
 
Rèn luyện kỹ năng giải toán phương trình lượng giác cho học sinh lớp 11 trung...
byjackjohn45
 

What's hot

DOC
130 tiểu luận về triết học
byluanvantrust
 
PDF
Tài liệu tham khảo trường điện từ
byCửa Hàng Vật Tư
 
PDF
Hang so Dirac - Ranh gioi giua vat ly co dien va vat ly luong tu
byLê Đại-Nam
 
PPTX
ĐỀ CƯƠNG BÀI TẬP KINH TẾ LƯỢNG (Thi viết).pptx
bycathien914
 
PDF
Chương 7: Ngân sách Nhà nước
byDzung Phan Tran Trung
 
PDF
Logic hoc
byĐời Du Mục
 
PPT
Hướng dẫn kế toán tài sản cố định
bytuvantfa
 
DOCX
Luận Văn Các Yếu Tố Ảnh Hưởng Đến Sự Hài Lòng Trong Công Việc Của Cán Bộ Công...
byHỗ Trợ Viết Đề Tài luanvanpanda.com
 
PDF
Bai giang-toan-kinh-te-tin-hoc
byLê Ngọc Huyền
 
PDF
Nguyen ly bat dinh Heisenberg va coherent states
byLê Đại-Nam
 
PDF
Nguyên lý thống kê chương 1
byHọc Huỳnh Bá
 
PDF
ứNg dụng phép biến đổi laplace giải một lớp các phương trình toán lý
byhttps://www.facebook.com/garmentspace
 
PPT
Bài thảo luận 3
byCassia Siêu Nhân
 
DOCX
Chuyên đề vật lý hạt nhân
byle hung
 
PDF
Tín Hiệu Và Hệ Thống - Phép biến đổi Laplace
byQuang Thinh Le
 
PDF
Phương pháp Sai phân hữu hạn trong truyền nhiệt
byTrinh Van Quang
 
PDF
Chuong1
bytuongnm
 
DOCX
Đường lối xây dựng phát triển văn hóa từ 1986
byVũ Ngọc Tú
 
PPT
ThiếT Kế Và đáNh Giá ThuậT ToáN
byguest717ec2
 
PPTX
Phan Cuc anh sang vật lý đai cương 3.pptx
byTnLnh6
 
130 tiểu luận về triết học
byluanvantrust
 
Tài liệu tham khảo trường điện từ
byCửa Hàng Vật Tư
 
Hang so Dirac - Ranh gioi giua vat ly co dien va vat ly luong tu
byLê Đại-Nam
 
ĐỀ CƯƠNG BÀI TẬP KINH TẾ LƯỢNG (Thi viết).pptx
bycathien914
 
Chương 7: Ngân sách Nhà nước
byDzung Phan Tran Trung
 
Logic hoc
byĐời Du Mục
 
Hướng dẫn kế toán tài sản cố định
bytuvantfa
 
Luận Văn Các Yếu Tố Ảnh Hưởng Đến Sự Hài Lòng Trong Công Việc Của Cán Bộ Công...
byHỗ Trợ Viết Đề Tài luanvanpanda.com
 
Bai giang-toan-kinh-te-tin-hoc
byLê Ngọc Huyền
 
Nguyen ly bat dinh Heisenberg va coherent states
byLê Đại-Nam
 
Nguyên lý thống kê chương 1
byHọc Huỳnh Bá
 
ứNg dụng phép biến đổi laplace giải một lớp các phương trình toán lý
byhttps://www.facebook.com/garmentspace
 
Bài thảo luận 3
byCassia Siêu Nhân
 
Chuyên đề vật lý hạt nhân
byle hung
 
Tín Hiệu Và Hệ Thống - Phép biến đổi Laplace
byQuang Thinh Le
 
Phương pháp Sai phân hữu hạn trong truyền nhiệt
byTrinh Van Quang
 
Chuong1
bytuongnm
 
Đường lối xây dựng phát triển văn hóa từ 1986
byVũ Ngọc Tú
 
ThiếT Kế Và đáNh Giá ThuậT ToáN
byguest717ec2
 
Phan Cuc anh sang vật lý đai cương 3.pptx
byTnLnh6
 

Similar to Lecture on Relativity theory - Chapter 2 Special Relativity

PPTX
Lecture on Relativity theory - Chapter 1 Relativity before Einstein
byLê Đại-Nam
 
PPTX
Lecture on Relativity theory - Chapter 3 General Relativity
byLê Đại-Nam
 
PPTX
Lecture on Relativity theory - Chapter 0 Introduction
byLê Đại-Nam
 
PPTX
Lecture1F1020
byThnhL251131
 
PDF
GR: Electric charges and gravitation field.
byLê Đại-Nam
 
PDF
Essay in Electrodynamics: Electromagnetic radiation
byLê Đại-Nam
 
PDF
Sự hình thành và phát triển lý thuyết sóng điện từ
byLee Ein
 
DOC
Thamluan hoithao sg_2010
byLe Vui
 
DOC
Thamluan hoithao sg_2010
bymahaxilin
 
DOCX
Thuyết tương đối hẹp thuyết tương đối cho mọi người
byfree lance
 
PDF
Thuyet thuong doi hep thuyết tương đối cho mọi người
byfree lance
 
PDF
Năng lượng và Lực Casimir trong trường vô hướng phức
bynguyenthamhn
 
PDF
Tóm tắt thuyết tương đối hẹp của Einstein
byLam Nguyen
 
PPTX
NHÓM 4 LỚP 10A6.ppptxlttslrtysrtylrlysl;45yl;ssr
byQuangLe156523
 
PDF
Ch 1- VL1etrthgbggrefdtrdfwififjwjfwioju.pdf
byngocminhnguyen5678
 
PDF
Luận văn: Quá trình tán xạ siêu hạt, HAY - Gửi miễn phí qua zalo=> 0909232620
byDịch vụ viết bài trọn gói ZALO: 0909232620
 
PDF
Tính chất quang, điện, từ của vật liệu1 1.pdf
bynguyenhoanlda
 
PDF
Chuyen de 8 so luoc ve thuyet tuong doi hep
byHuynh ICT
 
DOC
Lực quán tính và cách làm bài tập về lực quán tính
byLinh Nguyễn
 
PDF
vat-ly-dai-cuong-1__tom-tat-cong-thuc-vldc-i - [cuuduongthancong.com] - Copy.pdf
bytndngTn
 
Lecture on Relativity theory - Chapter 1 Relativity before Einstein
byLê Đại-Nam
 
Lecture on Relativity theory - Chapter 3 General Relativity
byLê Đại-Nam
 
Lecture on Relativity theory - Chapter 0 Introduction
byLê Đại-Nam
 
Lecture1F1020
byThnhL251131
 
GR: Electric charges and gravitation field.
byLê Đại-Nam
 
Essay in Electrodynamics: Electromagnetic radiation
byLê Đại-Nam
 
Sự hình thành và phát triển lý thuyết sóng điện từ
byLee Ein
 
Thamluan hoithao sg_2010
byLe Vui
 
Thamluan hoithao sg_2010
bymahaxilin
 
Thuyết tương đối hẹp thuyết tương đối cho mọi người
byfree lance
 
Thuyet thuong doi hep thuyết tương đối cho mọi người
byfree lance
 
Năng lượng và Lực Casimir trong trường vô hướng phức
bynguyenthamhn
 
Tóm tắt thuyết tương đối hẹp của Einstein
byLam Nguyen
 
NHÓM 4 LỚP 10A6.ppptxlttslrtysrtylrlysl;45yl;ssr
byQuangLe156523
 
Ch 1- VL1etrthgbggrefdtrdfwififjwjfwioju.pdf
byngocminhnguyen5678
 
Luận văn: Quá trình tán xạ siêu hạt, HAY - Gửi miễn phí qua zalo=> 0909232620
byDịch vụ viết bài trọn gói ZALO: 0909232620
 
Tính chất quang, điện, từ của vật liệu1 1.pdf
bynguyenhoanlda
 
Chuyen de 8 so luoc ve thuyet tuong doi hep
byHuynh ICT
 
Lực quán tính và cách làm bài tập về lực quán tính
byLinh Nguyễn
 
vat-ly-dai-cuong-1__tom-tat-cong-thuc-vldc-i - [cuuduongthancong.com] - Copy.pdf
bytndngTn
 

More from Lê Đại-Nam

PDF
[Essay] History of Classical Electrodynamics theory
byLê Đại-Nam
 
PDF
Essay in Statistical Mechanics: Boltzmann transport equation
byLê Đại-Nam
 
PDF
Homework 5 of QFT
byLê Đại-Nam
 
PDF
Homework 4 of QFT
byLê Đại-Nam
 
PDF
Homework 3 of QFT
byLê Đại-Nam
 
PDF
Homework 2 of Unifying interaction
byLê Đại-Nam
 
PDF
Homework 6 of Optical Semiconductor
byLê Đại-Nam
 
PDF
Homework 5 of Optical Semiconductor
byLê Đại-Nam
 
PDF
Homework 4 of Optical Semiconductor
byLê Đại-Nam
 
PDF
Homework 2 of Optical Semiconductor
byLê Đại-Nam
 
PDF
Homework 1 of Optical Semiconductor
byLê Đại-Nam
 
PDF
Homework 3 of Optical Semiconductor
byLê Đại-Nam
 
PDF
Report on Computational Biophysics: MD simulation of Caspase protein.
byLê Đại-Nam
 
PDF
on the unfinished beautiful theory gut su5
byLê Đại-Nam
 
PDF
on the de broglie's hypothesis of wave particle duality
byLê Đại-Nam
 
PDF
the exact analytical solution of harmonic oscillator problem
byLê Đại-Nam
 
PDF
On the fine structure of hydrogen
byLê Đại-Nam
 
PDF
Bai tap ve phuong phap bo va lcao
byLê Đại-Nam
 
PDF
Bai tap ve nguyen tu heli
byLê Đại-Nam
 
PDF
Bai tap nguyen li bien phan
byLê Đại-Nam
 
[Essay] History of Classical Electrodynamics theory
byLê Đại-Nam
 
Essay in Statistical Mechanics: Boltzmann transport equation
byLê Đại-Nam
 
Homework 5 of QFT
byLê Đại-Nam
 
Homework 4 of QFT
byLê Đại-Nam
 
Homework 3 of QFT
byLê Đại-Nam
 
Homework 2 of Unifying interaction
byLê Đại-Nam
 
Homework 6 of Optical Semiconductor
byLê Đại-Nam
 
Homework 5 of Optical Semiconductor
byLê Đại-Nam
 
Homework 4 of Optical Semiconductor
byLê Đại-Nam
 
Homework 2 of Optical Semiconductor
byLê Đại-Nam
 
Homework 1 of Optical Semiconductor
byLê Đại-Nam
 
Homework 3 of Optical Semiconductor
byLê Đại-Nam
 
Report on Computational Biophysics: MD simulation of Caspase protein.
byLê Đại-Nam
 
on the unfinished beautiful theory gut su5
byLê Đại-Nam
 
on the de broglie's hypothesis of wave particle duality
byLê Đại-Nam
 
the exact analytical solution of harmonic oscillator problem
byLê Đại-Nam
 
On the fine structure of hydrogen
byLê Đại-Nam
 
Bai tap ve phuong phap bo va lcao
byLê Đại-Nam
 
Bai tap ve nguyen tu heli
byLê Đại-Nam
 
Bai tap nguyen li bien phan
byLê Đại-Nam
 

Recently uploaded

PDF
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI NĂM 2024 HỆ THỐNG LÍ THUYẾT VÀ BÀI TẬP VỀ ĐIỆN TỬ ...
byNguyen Thanh Tu Collection
 
PDF
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI NĂM 2024 BÀI TẬP VỀ MẠCH PHI TUYẾN VÀ MẠCH ĐIỆN CH...
byNguyen Thanh Tu Collection
 
PDF
Đấu trường Vioedu lớp 5 cấp Khu vực, Phường, Xã năm 2025 - 2026 (Toán, Toán T...
byBồi Dưỡng HSG Toán Lớp 3
 
PDF
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI NĂM 2024 MẠCH ĐIỆN PHI TUYẾN LÝ THUYẾT VÀ PHƯƠNG P...
byNguyen Thanh Tu Collection
 
PDF
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI BẮC BỘ NĂM 2024 MÔN HÓA HỌC PHƯƠNG ÁN THỰC HÀNH PH...
byNguyen Thanh Tu Collection
 
PDF
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI BẮC BỘ NĂM 2024 MÔN HÓA HỌC PHƯƠNG ÁN THỰC HÀNH CH...
byNguyen Thanh Tu Collection
 
PDF
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI BẮC BỘ NĂM 2024 XÂY DỰNG 11 BÀI THỰC HÀNH ĐIỆN HÓA...
byNguyen Thanh Tu Collection
 
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI NĂM 2024 HỆ THỐNG LÍ THUYẾT VÀ BÀI TẬP VỀ ĐIỆN TỬ ...
byNguyen Thanh Tu Collection
 
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI NĂM 2024 BÀI TẬP VỀ MẠCH PHI TUYẾN VÀ MẠCH ĐIỆN CH...
byNguyen Thanh Tu Collection
 
Đấu trường Vioedu lớp 5 cấp Khu vực, Phường, Xã năm 2025 - 2026 (Toán, Toán T...
byBồi Dưỡng HSG Toán Lớp 3
 
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI NĂM 2024 MẠCH ĐIỆN PHI TUYẾN LÝ THUYẾT VÀ PHƯƠNG P...
byNguyen Thanh Tu Collection
 
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI BẮC BỘ NĂM 2024 MÔN HÓA HỌC PHƯƠNG ÁN THỰC HÀNH PH...
byNguyen Thanh Tu Collection
 
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI BẮC BỘ NĂM 2024 MÔN HÓA HỌC PHƯƠNG ÁN THỰC HÀNH CH...
byNguyen Thanh Tu Collection
 
CHUYÊN ĐỀ CHUYÊN DUYÊN HẢI BẮC BỘ NĂM 2024 XÂY DỰNG 11 BÀI THỰC HÀNH ĐIỆN HÓA...
byNguyen Thanh Tu Collection
 

Lecture on Relativity theory - Chapter 2 Special Relativity

  • 1.
    LÝ THUYẾT TƯƠNGĐỐI Chương 2: Lý thuyết tương đối hẹp và hệ quả 22/02/2019Dai-Nam Le 1
  • 2.
    NỘI DUNG Lý thuyết tương đối và hệ quả Quátrình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 2
  • 3.
    Quá trình rađời Lý thuyết tương đối Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 3 Lý thuyết tương đối và hệ quả
  • 4.
    Quá trình rađời Lý thuyết tương đối 22/02/2019Dai-Nam Le 4 Giả thiết Aether và tương thích giữa CH và ĐĐL Vấn đề về khối lượng của điện tích chuyển động
  • 5.
    Quá trình rađời Lý thuyết tương đối 22/02/2019Dai-Nam Le 5 Giả thiết Aether và tương thích giữa CH và ĐĐL
  • 6.
    22/02/2019Dai-Nam Le 6 Quátrình ra đời Lý thuyết tương đối
  • 7.
    1907 – 1908,không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 7 Quá trình ra đời Lý thuyết tương đối 1887, xây dựng một phép biến đổi thay thế phép biến đổi Galilei cho Điện động lực . Woldemar Voigt
  • 8.
    1907 – 1908,không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 8 Quá trình ra đời Lý thuyết tương đối Oliver Heaviside 𝑬, 𝑩 của điện tích chuyển động Joshep John Thomson Khảo sát 𝑩 gây ra bởi điện tích chuyển động trong 𝑬 Đưa ra một biểu thức tương tự co ngắn Lorentz-FitzGerald George F. C. Searle Khảo sát biến dạng của Elip Heaviside
  • 9.
    1907 – 1908,không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 9 Quá trình ra đời Lý thuyết tương đối George Francis FitzGerald 1889, Đưa ra giả thuyết Hiệu ứng co ngắn Lorentz-FitzGerald Joseph Larmor 1897, đưa ra phép biến đổi tương tự Voigt, có một chút khác biệt. 1900, đưa ra phép biến đổi Lorentz
  • 10.
    1907 – 1908,không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 10 Quá trình ra đời Lý thuyết tương đối 1892, đưa ra giả thuyết Hiệu ứng co ngắn Lorentz-FitzGerald. Ông cũng đưa ra một phép biến đổi mà 1897 Larmor đưa ra. Sau đó, ông đưa ra một loạt dạng phép biến đổi giữa 2 HQC quán tính. 1904, ông đưa ra được phép biến đổi Lorentz giữa 2 HQC quán tính. Áp dụng phép biến đổi Lorentz cho hệ phương trình Maxwell-Lorentz cho trường tự do. Hendrik Antoon Lorentz
  • 11.
    1907 – 1908,không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 11 Quá trình ra đời Lý thuyết tương đối Jules Henri Poincaré 1900, khảo sát tính tương đối của khái niệm “đồng thời”. 1905, viết lại phép biến đổi Lorentz theo dạng đối xứng (hiện đại); đưa ra “nhóm Lorentz”. Áp dụng phép biến đổi Lorentz cho hệ phương trình Maxwell-Lorentz tổng quát  bước đầu phát biểu được Nguyên lý tương đối tổng quát. Bước đầu xây dựng không thời gian 4 chiều 𝒙, 𝒚, 𝒛, 𝒊𝒄𝒕
  • 12.
    1907 – 1908,không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 12 Quá trình ra đời Lý thuyết tương đối Albert Einstein 1905, công bố bài báo Zur Elektrodynamik bewegter Körper Trong đó: • Mở rộng Nguyên lý tương đối • Công nhận c = const. • Bác bỏ giả thiết Aether • Phép biến đổi Lorentz (độc lập) • Khảo sát các hệ quả: vd biểu thức cộng vận tốc, hiệu ứng Dopler, động năng của một hạt chuyển động, …
  • 13.
    1907 – 1908,không thời gian Minkowski 1900 – 1905, nhóm Lorentz + NL tương đối 1905, 2 tiên đề + bác bỏ aether Hermann Minkowski Jules Henri Poincaré Albert Einstein 1892 – 1904, phép biến đổi Lorentz Hendrik Antoon Lorentz 22/02/2019Dai-Nam Le 13 Quá trình ra đời Lý thuyết tương đối Hermann Minkowski 1907 – 1908, xây dựng • Không gian Minkowski + hình học của nó • Động học, Động lực học 4 chiều • Điện động lực 4 chiều Qua đó, biểu diễn lại phép biến đổi Lorentz bằng cách dùng giản đồ Minkowski
  • 14.
    Quá trình rađời Lý thuyết tương đối 22/02/2019Dai-Nam Le 14 Vấn đề về khối lượng của điện tích chuyển động
  • 15.
    Quá trình rađời Lý thuyết tương đối 22/02/2019Dai-Nam Le 15 Từ TN của Thomson J. J. Thomson M. Abraham H. A. Lorentz Từ Áp suất ánh sáng J. H. Poincaré F. Hasenöhrl Năng lượng = Quán tính A. Einstein electron chuyển động trong Aether + lực cản nhớt Stokes Áp suất ánh sáng  m của trường điện từ phụ thuộc vào E Động năng của hạt chuyển động  𝑬 = 𝒎𝒄 𝟐
  • 16.
    Quá trình rađời Lý thuyết tương đối 22/02/2019Dai-Nam Le 16 Albert Einstein Trong “Zur Elektrodynamik bewegter Körper“, Einstein đã xác định được động năng của một hạt chuyển động.  Einstein bắt đầu có những suy nghĩ về liên hệ giữa khối lượng và năng lượng  Ông tiếp tục công bố bài báo thứ hai.
  • 17.
    Quá trình rađời Lý thuyết tương đối 22/02/2019Dai-Nam Le 17 Albert Einstein Trong năm 1905, công bố bài báo “Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?“ Thông qua TN tưởng tượng, Einstein gián tiếp đồng nhất khối lượng quán tính 𝒎 với năng lượng 𝑬
  • 18.
    Quá trình rađời Lý thuyết tương đối 22/02/2019Dai-Nam Le 18 Albert Einstein
  • 19.
    Khối lượng quántính phải giảm xuống! Quá trình ra đời Lý thuyết tương đối 22/02/2019Dai-Nam Le 19 Albert Einstein ∆𝒎 = − 𝑬 𝒃ứ𝒄 𝒙ạ 𝒄 𝟐
  • 20.
    Quá trình rađời Lý thuyết tương đối 22/02/2019Dai-Nam Le 20
  • 21.
    Hai tiên đềEinstein, phép biến đổi Lorentz Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 21 Lý thuyết tương đối và hệ quả
  • 22.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 22 Tiên đề 1: Nguyên lý tương đối
  • 23.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 23 Tiên đề 1: Nguyên lý tương đối
  • 24.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 24 Tiên đề 1: Nguyên lý tương đối Mọi hiện tượng vật lý đều diễn ra như nhau trong mọi hệ quy chiếu quán tính. • Mở rộng Nguyên lý tương đối của Galilei cho mọi hiện tượng vật lý: bao gồm cả Cơ, Nhiệt, Điện Từ, Quang, …. • Như nhau  các PT vật lý giữ nguyên dạng  Không có HQC ưu tiên, do đó không có aether.
  • 25.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 25 Tiên đề 2: Tính bất biến của vận tốc ánh sáng trong chân không Vận tốc ánh sáng trong chân không c không phụ thuộc vào chuyển động của nguồn sáng. • Trong nhiều giả thiết khác nhau, Einstein cho rằng chỉ cần sử dụng tiên đề này + Nguyên lý tương đối là đủ. • Lưu ý: trong tiên đề này chỉ đề cập đến vận tốc ánh sáng trong chân không • Hệ quả: không có vận tốc vật lý nào lớn hơn c  giả định về tachyon.
  • 26.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 26 Sự kiện – Hệ quy chiếu Sự kiện được xác định bởi vị trí trong không gian (x, y, z) và thời điểm (t) 𝑥, 𝑦, 𝑧, 𝑡 Hệ quy chiếu bao gồm • Vật làm mốc • Hệ trục tọa độ + thước • Mốc thời gian + hệ đồng hồ đồng bộ
  • 27.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 27 Hệ đồng hộ đồng bộ Xảy ra: 𝑡0 = 0 Nhận được thông tin: 𝑡 = 𝐿 𝑐
  • 28.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 28 Hệ đồng hộ đồng bộ 𝑡 = 0𝑡 = 0 𝑡′ = 𝐿 𝑐 𝑡′ = 𝐿 𝑐 Sử dụng 2 đồng hồ đồng bộ
  • 29.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 29 Hệ đồng hộ đồng bộ x
  • 30.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 30 Hệ đồng hộ đồng bộ O x y z • Mỗi điểm trong không gian có một đồng hồ • Tất các các đồng hồ tạo thành một hệ đồng hồ. • Hệ đồng hồ này được đồng bộ với nhau.  Bác bỏ tính đồng thời theo cách hiểu của cơ học cổ điển.
  • 31.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 31 Phép biến đổi Lorentz x y z O x’ y’ z’ O’ 𝑉 Tại 𝑡 = 𝑡′ = 0 thì 𝑥 = 𝑥′ = 0 𝑦 = 𝑦′, 𝑧 = 𝑧′. Có nhiều cách xây dựng  Cách xây dựng của Einstein trong “Relativity: The Special and General Theory” (11)
  • 32.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 32 Phép biến đổi Lorentz x y z O x’ y’ z’ O’ 𝑉 Xung ánh sáng 1 Trong hệ K: 𝑥 = 𝑐𝑡 Trong hệ K’: 𝑥′ = 𝑐𝑡′  𝑥′ − 𝑐𝑡′ = 𝑎 𝑥 − 𝑐𝑡
  • 33.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 33 Phép biến đổi Lorentz x y z O x’ y’ z’ O’ 𝑉Xung ánh sáng 2 Trong hệ K: 𝑥 = − 𝑐𝑡 Trong hệ K’: 𝑥′ = − 𝑐𝑡′  𝑥′ + 𝑐𝑡′ = 𝑏 𝑥 + 𝑐𝑡
  • 34.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 34 Phép biến đổi Lorentz x y z O x’ y’ z’ O’ 𝑉 Đối với gốc O’ Trong hệ K: 𝑥 = 𝑉𝑡 Trong hệ K’: 𝑥′ = 0
  • 35.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 35 Phép biến đổi Lorentz Tổng hợp lại, ta có 3 phương trình 𝑥′ − 𝑐𝑡′ = 𝑎 𝑥 − 𝑐𝑡 (I) 𝑥′ + 𝑐𝑡′ = 𝑏 𝑥 + 𝑐𝑡 (II) 𝑥′ = 0, 𝑥 = 𝑣𝑡 (III) Từ (I) và (II) ta giải ra 𝑥′ = 𝑎+𝑏 2 𝑥 + 𝑏−𝑎 2 𝑐𝑡 (IV) 𝑡′ = 𝑎+𝑏 2 𝑡 + 𝑏−𝑎 2𝑐 𝑥 (V) Thay (IV), (V) vào (III) 𝑎−𝑏 𝑎+𝑏 = 𝑉 𝑐 (VI) Từ (VI), ta viết lại (IV), (V) thành 𝑥′ = 𝜅 𝑥 − 𝑉𝑡 (VII) 𝑡′ = 𝜅 𝑡 − 𝑉 𝑐2 𝑥 (VIII)
  • 36.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 36 Phép biến đổi Lorentz Từ phép biến đổi (VII) và (VIII), ta xây dựng phép biến đổi ngược 𝑥 = 1 𝜅 1− 𝑉2 𝑐2 𝑥′ + 𝑉𝑡′ (IX) 𝑡 = 1 𝜅 1− 𝑉2 𝑐2 𝑡′ + 𝑉 𝑐2 𝑥′ (X) Do phép biến đổi giữa K và K’ là đối xứng nên 1 𝜅 1− 𝑉2 𝑐2 = 𝜅 Hay 𝜿 = 𝟏 𝟏− 𝑽 𝟐 𝒄 𝟐 (XI)
  • 37.
    Hai tiên đềEinstein, phép biến đổi Lorentz 22/02/2019Dai-Nam Le 37 Phép biến đổi Lorentz Tổng hợp lại, ta có phép biến đổi Lorentz giữa K và K’ 𝒙′ = 𝒙−𝑽𝒕 𝟏− 𝑽 𝟐 𝒄 𝟐 𝒚′ = 𝒚 𝒛′ = 𝒛 𝒕′ = 𝒕− 𝑽 𝒄 𝟐 𝒙 𝟏− 𝑽 𝟐 𝒄 𝟐 Thừa số Lorentz 𝛾 = 1 1− 𝑉2 𝑐2
  • 38.
    22/02/2019Dai-Nam Le 38 Câuhỏi: Hãy áp dụng phép biến đổi Lorentz để biến đổi phương trình truyền sóng điện từ trong HQC K ΔΨ = 1 𝑐2 𝜕2Ψ 𝜕𝑡2 để viết lại phương trình truyền sóng điện từ trong HQC K’. Hai tiên đề Einstein, phép biến đổi Lorentz Câu hỏi: Hãy so sánh 𝑐2 𝑡2 − 𝑥2 − 𝑦2 − 𝑧2 và 𝑐2 𝑡′2 − 𝑥′2 − 𝑦′2 − 𝑧′2
  • 39.
    Không gian Minkowski,giản đồ Minkowski Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 39 Lý thuyết tương đối và hệ quả
  • 40.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 40 Không gian Minkowski (Không thời gian Minkowski) Không gian Euclide (Không gian vector) x y z O 𝑟 = 𝑥, 𝑦, 𝑧 M (x,y,z) • Các tiên đề của KG Euclide • Các tiên đề về tích vô hướng Vector 𝑟 = 𝑥, 𝑦, 𝑧 ≡ 𝑥1, 𝑥2, 𝑥3 Tích vô hướng 𝑎 ⋅ 𝑏 = 𝑗=1 3 𝑎 𝑗 𝑏 𝑗 Khoảng các giữa hai điểm gần nhau 𝒅𝒍 𝟐 = 𝒅𝒙 𝟏 𝒅𝒙 𝟏 + 𝒅𝒙 𝟐 𝒅𝒙 𝟐+𝒅𝒙 𝟑 𝒅𝒙 𝟑
  • 41.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 41 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Là một không gian chuẩn Euclide (pseudo-Euclidean space) • Mỗi vector gồm 4 thành phần: 1 vô hướng + 3 có hướng • Để thuận tiện, vector 4 chiều được chia làm hai loại  Vector phản biến: 𝑎 𝜇 (gồm 1 vô hướng + 3 (+ có hướng))  Vector hiệp biến: 𝑎 𝜇 (gồm 1 vô hướng + 3 (- có hướng))  Liên hệ giữa vector thường biến và hiệp biến 𝑎0 = 𝑎0, 𝑎1 = − 𝑎1, 𝑎2 = − 𝑎2, 𝑎3 = − 𝑎3 ⟹ 𝑎 𝜇 = 𝜈=0 3 𝜂 𝜇𝜈 𝑎 𝜈 = 𝜂 𝜇𝜈 𝑎 𝜈 Quy ước Einstein
  • 42.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 42 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Minkowski metric tensor: 𝜂 𝜇𝜈 = +1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 −1 • Quy tắc nâng hạ chỉ số: khi nâng hạ chỉ số của vector (và các tensor hạng cao) thì  Thành phần ứng với chỉ số 0: không đổi dấu  Thành phần ứng với các chỉ số khác: đổi dấu.
  • 43.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 43 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Tích vô hướng được trang bị 𝑎 ⋅ 𝑏 = 𝜇=0 3 𝑎 𝜇 𝑏 𝜇 = 𝑎 𝜇 𝑏 𝜇 = 𝜂 𝜇𝜈 𝑎 𝜇 𝑏 𝜈 = 𝑎0 𝑏0 − 𝑎1 𝑏1 − 𝑎2 𝑏2 − 𝑎3 𝑏3 • Norm của vector 4 chiều 𝑎 𝑎 2 = 𝑎 ⋅ 𝑎 = 𝑎 𝜇 𝑎 𝜇 = 𝜂 𝜇𝜈 𝑎 𝜇 𝑎 𝜈 = 𝑎0 𝑎0 − 𝑎1 𝑎1 − 𝑎2 𝑎2 − 𝑎3 𝑎3
  • 44.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 44 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Phép biến đổi Lorentz cho vector phản biến có thể viết dưới dạng 𝑎′ 𝜇 = Λ 𝜇 𝜈 𝑎 𝝂 trong đó (TH 𝑉 song song trục x) Λ 𝜇 𝜈 = 𝛾 −𝛽𝛾 0 0 −𝛽𝛾 𝛾 0 0 0 0 +1 0 0 0 0 +1 𝛽 = 𝑉 𝑐 Tích vô hướng bất biến với phép biến đổi Lorent
  • 45.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 45 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski • Biến cố (Sự kiện) được xác định bởi 𝒙, 𝒚, 𝒛, 𝒕 • Vector phản biến ứng với biến cố: 𝒙 𝝁 = 𝒄𝒕, + 𝒙, + 𝒚, + 𝒛 • Vector hiệp biến ứng với biến cố: 𝒙 𝝁 = 𝒄𝒕, − 𝒙, − 𝒚, − 𝒛 • Khoảng giữa hai biến cố lân cận nhau ds 𝒅𝒔 𝟐 = 𝒅𝒙 𝝁 𝒅𝒙 𝝁 = 𝜼 𝝁𝝂 𝒅𝒙 𝝁 𝒅𝒙 𝝂 Metric Minkowski (phẳng)Khoảng ds là một bất biến đối với phép biến đổi Lorentz
  • 46.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 46 Không gian Minkowski (Không thời gian Minkowski) Không gian Minkowski Không thời gian (1+3) chiều gồm  1 chiều thời gian ct  3 chiều không gian x, y, z
  • 47.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 47 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02)
  • 48.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 48 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02)
  • 49.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 49 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02)
  • 50.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 50 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x 𝒗 < 𝒄
  • 51.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 51 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x 𝑣
  • 52.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 52 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x A B E Đối với I
  • 53.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 53 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x A B E Đối với A’ B’ I
  • 54.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 54 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x A B E Theo tiên đề 2 • I là trung điểm của AB • E là trung điểm của A’B’ A’ B’ I Trong hệ K: A và B đồng thời Trong hệ K’: A’ và B’ đồng thời
  • 55.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 55 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’
  • 56.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 56 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ 𝜓 𝜓 tan 𝜓 = 𝑣 𝑐
  • 57.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 57 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ 𝑖𝜑 𝑖𝜑 tanh 𝜑 = 𝑣 𝑐 Phép quay trục góc ảo 𝑖𝜑
  • 58.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 58 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ Biến cố x’ ct’ x ct
  • 59.
    ‘ ‘ ‘‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ ‘ Không gian Minkowski, giản đồ Minkowski 22/02/2019Dai-Nam Le 59 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ Thước Hệ đồng hồ
  • 60.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 60 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x ct’ x’ 1 1’ 1 1’ 2 2 2’ 2’ 𝑠2 = 𝑐𝑡 2 − 𝑥 2  mặt hyperbola  Xác định tỉ lệ độ chia giữa K và K’ 𝑠2 = −1 𝑠2 = −2
  • 61.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 61 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) ct O x 𝒗 < 𝒄 Khoảng loại thời gian 𝑑𝑠2 > 0 Khoảng loại không gian 𝑑𝑠2 < 0
  • 62.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 62 Không gian Minkowski (Không thời gian Minkowski) Giản đồ Minkowski (tham khảo thêm tài liệu 02) Khoảng loại thời gian 𝑑𝑠2 > 0 - Bên trong nón ánh sáng - Tìm được HQC hai biến cố xảy ra cùng nơi. Khoảng loại không gian 𝑑𝑠2 < 0 - Bên ngoài nón ánh sáng - Tìm được HQC hai biến cố xảy ra cùng lúc.
  • 63.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 63 Không gian Minkowski (Không thời gian Minkowski) Câu hỏi ct O x ct’ x’ x ct Với phép quay trục trên, chứng tỏ rằng vận tốc ánh sáng trong chân không c là hằng số? 𝜓 𝜓
  • 64.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 64 Không gian Minkowski (Không thời gian Minkowski) Câu hỏi ct O x ct’ x’ Biến cố x’ ct’ x ct Hãy dẫn ra phép biến đổi Lorentz từ giản đồ Minkowski bên cạnh với tan 𝜓 = 𝑣 𝑐 𝜓 𝜓
  • 65.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 65 Không gian Minkowski (Không thời gian Minkowski) Câu hỏi Tại sao phép biến đổi Lorentz là phép quay với góc ảo 𝑖𝜑 tanh 𝜑 = 𝑣 𝑐 ct O x ct’ x’ 𝑖𝜑 𝑖𝜑
  • 66.
    Không gian Minkowski,giản đồ Minkowski 22/02/2019Dai-Nam Le 66 Không gian Minkowski (Không thời gian Minkowski) Câu hỏi CMR: - Bên trong nón ánh sáng tìm được một HQC hai biến cố xảy ra cùng nơi. - Bên ngoài nón ánh sáng tìm được một HQC hai biến cố xảy ra cùng lúc.
  • 67.
    CH, ĐĐL vàCHLT tương đối tính Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 67 Lý thuyết tương đối và hệ quả
  • 68.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 68 a) Động học 𝑑𝑠2 > 0 ⇒ 𝑑𝑠2 = 𝑐𝑑𝜏 2 𝑑𝑠2 < 0 ⇒ 𝑑𝑠2 = − 𝑑𝑙 2 Thời gian riêng Khoảng cách riêng ct O x 𝑑𝜏 𝑑𝑙 Tổng quát thì ta dùng 𝑑𝜏 thay cho 𝑑𝜏 và 𝑑𝑟
  • 69.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 69 a) Động học Vận tốc 3 chiều 𝑢 = 𝑑 𝑟 𝑑𝑡 Vận tốc 4 chiều 𝑢 𝜇 = 𝑑𝑥 𝜇 𝑑𝜏 = 𝑐𝑑𝑡 𝑑𝜏 , 𝑑 𝑟 𝑑𝜏 ct O x 𝑢 𝜇
  • 70.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 70 a) Động học Kết hợp 𝑑𝜏 𝑑𝑡 = 1 𝛾 𝑢 ct O x 𝑢 𝜇
  • 71.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 71 a) Động học Suy ra được 𝑢 𝜇 = 𝛾 𝑢 𝑐, 𝑢 ct O x 𝑢 𝜇 3 chiều vector 1 chiều vô hướng
  • 72.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 72 1. Hãy xác định phép biến đổi Lorentz cho vector vận tốc 4 chiều. 2. Chứng minh rằng norm của vector vận tốc 4 chiều 𝑢 = 𝑢 𝜇 𝑢 𝜇 là một bất biến tương đối tính. Câu hỏi
  • 73.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 73 a) Động học Vector gia tốc 4 chiều 𝑎 𝜇 = 𝑑𝑢 𝜇 𝑑𝜏 Vector gia tốc 4 chiều trực giao với vector vận tốc 4 chiều 𝑎 ∙ 𝑢 = 𝑎 𝜇 𝑢 𝜇 = 0 ct O x 𝑢 𝜇 𝑎 𝜇
  • 74.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 74 b) Động lực học Đi từ định luật 2 Newton Xây dựng động lượng 4 chiều Đi từ nguyên lý tác dụng tối thiểu Xây dựng hàm tác dụng cho hạt tự do
  • 75.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 75 b) Động lực học Tác dụng 𝑆 → bất biến tương đối tính Hạt tự do cổ điển 𝑆 𝑐ổ đ𝑖ể𝑛 = 𝑚 2 𝑡 𝑖 𝑡 𝑓 𝑢 ∙ 𝑑 𝑟 𝑢 ∙ 𝑑𝑥 = 𝑢 𝜇 𝑑𝑥 𝜇 là bất biến ct O 𝑟 i f Bất biến với phép biến đổi Galilei
  • 76.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 76 b) Động lực học Tác dụng của hạt tự do có dạng 𝑆 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = 𝛼 𝑡 𝑖 𝑡 𝑓 𝑢 ∙ 𝑑𝑥 có thể viết lại thành 𝑆 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = 𝑡 𝑖 𝑡 𝑓 𝛼 𝑐2 𝛾𝑢 𝑑𝑡 ct O 𝑟 i f Hàm Lagrange
  • 77.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 77 b) Động lực học Hàm Lagrange của hạt tự do 𝐿 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = 𝛼 𝑐2 𝛾𝑢 = 𝛼 𝑐2 1 − 𝑢2 𝑐2 Khai triển Taylor 𝐿 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = 𝛼 𝑐2 − 𝛼 𝑢2 2 − 𝛼 𝑢4 8𝑐2 𝐿 𝑐ổ đ𝑖ể𝑛 = 𝑚0 𝑢2 2 𝜶 = −𝒎 𝟎
  • 78.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 78 b) Động lực học Vậy, hàm Lagrange của hạt tự do 𝐿 𝑡ươ𝑛𝑔 đố𝑖 𝑡í𝑛ℎ = − 𝑚0 𝑐2 1 − 𝑢2 𝑐2  động lượng và năng lượng của hạt tự do 𝑝 = 𝛾𝑢 𝑚0 𝑢 𝐸 = 𝛾𝑢 𝑚0 𝑐2 Khối lượng tương đối
  • 79.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 79 b) Động lực học Vector năng - động lượng 4 chiều 𝑝 𝜇 = 𝑚0 𝑢 𝜇 = 𝑚0 𝛾 𝑢 𝑐, 𝑢 𝒑 𝝁 = 𝑬 𝒄 , 𝒑 ct O x 𝑢 𝜇 3 chiều 𝑝 = 𝛾𝑢 𝑚0 𝑢 1 chiều 𝐸 = 𝛾𝑢 𝑚0 𝑐2 Năng – động lượng cũng biến đổi Lorentz 𝑝 𝜇 𝐸/𝑐 𝑝
  • 80.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 80 b) Động lực học Định luật II Newton tương đối tính (từ Pt Euler-Lagrange) 𝐹 = 𝑑 𝑝 𝑑𝑡 = 𝑑 𝛾𝑢 𝑚0 𝑢 𝑑𝑡 Định lí động năng 𝐹 ∙ 𝑢 = 𝑑𝐸 𝑑𝑡 = 𝑑 𝛾𝑢 𝑚0 𝑐2 𝑑𝑡
  • 81.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 81 b) Động lực học Đưa 𝑝 𝜇 = 𝑚0 𝑢 𝜇 = 𝐸 𝑐 , 𝑝 vào, ta có định luật II Newton 4 chiều 𝐹 𝜇 = 𝑑𝑝 𝜇 𝑑𝜏 Khái niệm lực 4 chiều 𝐹 𝜇 = 𝛾𝑢 𝐹 ∙ 𝑢 𝑐 , 𝐹 Lực cũng biến đổi Lorentz
  • 82.
    CH, ĐĐL vàCHLT tương đối tính 1. Cơ học tương đối tính Dai-Nam Le 22/02/2019 82 b) Động lực học Định luật bảo toàn năng – động lượng 4 chiều 𝐹 𝜇 = 0 ⟹ 𝑑𝑝 𝜇 𝑑𝜏 = 0 Do đó 𝑑𝐸 𝑑𝑡 = 0 và 𝑑 𝑝 𝑑𝑡 = 0 Áp dụng cho bài toán va chạm
  • 83.
    CH, ĐĐL vàCHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 83 + 𝐸
  • 84.
    CH, ĐĐL vàCHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 84 + 𝐸′ 𝑡 − 𝑟 𝑐 𝑟 = 𝑐𝑡 𝐼 𝐵′ 𝑡𝐸 → 𝐸′, 𝐵′
  • 85.
    CH, ĐĐL vàCHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 85 + 𝐵 + + ++ + + + + - - - -- - - - -
  • 86.
    CH, ĐĐL vàCHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 86 𝐵′ + - - - -- - - - - ++ ++ +++ + 𝐸′ 𝐵 → 𝐸′, 𝐵′
  • 87.
    CH, ĐĐL vàCHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 87 Điện trường và từ trường cũng biến đổi (Lorentz) Xét trường hợp trường điện từ tự do trong HQC K 𝛻 ∙ 𝐸 = 0 𝛻 ∙ 𝐵 = 0 𝛻 × 𝐸 = − 𝜕𝐵 𝜕𝑡 𝛻 × 𝐵 = 1 𝑐2 𝜕𝐸 𝜕𝑡 và HQC K’ 𝛻′ ∙ 𝐸′ = 0 𝛻′ ∙ 𝐵′ = 0 𝛻′ × 𝐸′ = − 𝜕𝐵′ 𝜕𝑡′ 𝛻′ × 𝐵′ = 1 𝑐2 𝜕𝐸′ 𝜕𝑡′
  • 88.
    CH, ĐĐL vàCHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 88 Đồng nhất hai PT, ta được phép biến đổi cho các vector cường độ (tham khảo tài liệu 10) 𝐸′ 𝑥 = 𝐸 𝑥 𝐸′ 𝑦 = 𝛾 𝐸 𝑦 − 𝑉𝐵𝑧 𝐸′ 𝑧 = 𝛾 𝐸𝑧 + 𝑉𝐵𝑦 𝐵′ 𝑥 = 𝐵𝑥 𝐵′ 𝑦 = 𝛾 𝐵𝑦 + 𝑉 𝑐2 𝐸𝑧 𝐵′ 𝑧 = 𝛾 𝐵𝑧 − 𝑉 𝑐2 𝐸 𝑦 Tương tự, ta cũng có thể dẫn ra phép biến đổi cho các vector cảm ứng 𝐷′ 𝑥 = 𝐷 𝑥 𝐷′ 𝑦 = 𝛾 𝐷 𝑦 − 𝑉 𝑐2 𝐻𝑧 𝐷′ 𝑧 = 𝛾 𝐷𝑧 + 𝑉 𝑐2 𝐻 𝑦 𝐻′ 𝑥 = 𝐻 𝑥 𝐻′ 𝑦 = 𝛾 𝐻 𝑦 + 𝑉𝐷𝑧 𝐻′ 𝑧 = 𝛾 𝐻𝑧 − 𝑉𝐷 𝑦
  • 89.
    CH, ĐĐL vàCHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 89 Khi có nguồn (mật độ điện tích và mật độ dòng) thì phép biến đổi Lorentz của các đại lượng nguồn là 𝑗′ 𝑥 = 𝛾 𝑗 𝑥 − 𝜌𝑉 𝑗′ 𝑦 = 𝑗 𝑦 𝑗′ 𝑧 = 𝑗′ 𝑧 𝜌′ = 𝛾 𝜌 − 𝑉𝑗 𝑥 𝑐2 Vector mật độ dòng 4 chiều 𝑗 𝜇 = 𝑐𝜌, 𝑗 Có thể viết dưới dạng vector 4 chiều
  • 90.
    CH, ĐĐL vàCHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 90 Đối với các vector cường độ (cảm ứng): ta có 2 vector  6 thành phần ” Không viết dưới dạng vector 4 chiều được ” Tensor 4 chiều hạng 2, có 42 = 𝟏𝟔 thành phần ” Ta có 6 thành phần độc lập nên phải là tensor phản xứng ! Tensor cường độ trường điện từ 𝐹 𝜇𝜈 = 0 − 𝐸𝑥 𝑐 − 𝐸 𝑦 𝑐 −𝐸𝑧 𝑐 𝐸𝑥 𝑐 0 −𝐵𝑧 𝐵𝑦 𝐸 𝑦 𝑐 𝐵𝑧 0 −𝐵𝑥 𝐸𝑧 𝑐 −𝐵𝑦 𝐵𝑥 0
  • 91.
    CH, ĐĐL vàCHLT tương đối tính 2. Điện động lực học tương đối tính Dai-Nam Le 22/02/2019 91 Phép biến đổi Lorentz của tensor cường độ trường điện từ 𝐹′ 𝛼𝛽 = 𝛬 𝛼 𝜇 𝛬 𝛽 𝜈 𝐹 𝜇𝜈 Chứng minh rằng 𝐹 𝜇𝜈 𝐹𝜇𝜈 = 2 𝐵2 − 1 𝑐2 𝐸2 là một bất biến tương đối tính.
  • 92.
    CH, ĐĐL vàCHLT tương đối tính 22/02/2019Dai-Nam Le 92 2. Điện động lực học tương đối tính Hiệu ứng Dopler tương đối tính Áp dụng phép biến đổi Lorentz của trường điện từ cho trường hợp của sóng điện từ, ta chứng minh được 𝑘 𝜇 = 𝑐𝜔, 𝑘 là một vector 4 chiều. Từ phép biến đổi Lorentz của 𝑘 𝜇, ta có 𝑓 𝑀 1 − 𝑣 𝑀 2 𝑐2 1 − 𝑣 𝑀 𝑐 cos 𝜃 𝐶𝑀 = 𝑓𝑆 1 − 𝑣 𝑆 2 𝑐2 1 − 𝑣 𝑆 𝑐 cos 𝜃 𝐶𝑆
  • 93.
    CH, ĐĐL vàCHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 93 Cơ học lượng tử phi tương đối tính  PT Schroedinger 𝐸 = 𝑇 + 𝑈 = 𝑝2 2𝑚 + 𝑈 Thay 𝐸 → +𝑖ℏ 𝜕 𝜕𝑡 𝑝 → −𝑖ℏ𝛻 Ta được PT Schroedinger 𝑖ℏ 𝜕 𝜕𝑡 Ψ = − ℏ2 2𝑚 𝛻2 Ψ + 𝑈Ψ
  • 94.
    CH, ĐĐL vàCHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 94 Cơ học lượng tử tương đối tính  PT Klein – Gordon 𝐸 = 𝑝2 𝑐2 + 𝑚2 𝑐4 + 𝑈 Thay 𝐸 → +𝑖ℏ 𝜕 𝜕𝑡 𝑝 → −𝑖ℏ𝛻 Ta được PT Klein – Gordon 𝑖ℏ 𝜕 𝜕𝑡 − 𝑈 2 Ψ = −ℏ2 𝑐2 𝛻2 Ψ + 𝑚2 𝑐4Ψ PT này tồn tại nhiều vấn đề nên không phải là mở rộng PT Schroedinger trong giới hạn tương đối tính cho 1 hạt. PT này sử dụng để mô tả 1 hệ hạt spin nguyên (boson)
  • 95.
    CH, ĐĐL vàCHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 95 Áp dụng PT Klein – Gordon cho hạt tự do □Ψ = 𝑚2 𝑐2 ℏ2 Ψ Thế Yukawa trong tương tác giữa nucleon – nucleon 𝑈 𝑌𝑢𝑘𝑎𝑤𝑎~ 𝑒−𝜆𝑟 𝑟 là nghiệm của PT □𝑈 𝑌𝑢𝑘𝑎𝑤𝑎 = λ2 𝑈 𝑌𝑢𝑘𝑎𝑤𝑎 Dự đoán 𝑚𝑐 ℏ = 𝜆~ 1 𝑅0 ⟹ 𝑚 = ℏ 𝑅0 𝑐 ~200 ÷ 300 𝑚 𝑒
  • 96.
    CH, ĐĐL vàCHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 96 Cơ học lượng tử tương đối tính  PT Dirac 𝑝 𝜇 𝑝 𝜇 = 𝑚2 𝑐4 Thay 𝑝 𝜇 → 𝛼1 𝜕 𝑥 + 𝛼2 𝜕 𝑦 + 𝛼3 𝜕𝑧 + 𝛽𝜕𝑡 Các “hệ số” 𝛼1, 𝛼2, 𝛼3, 𝛽 phải là các ma trận vuông 4 chiều ” Hàm sóng lưỡng spinor PT cho cơ học lượng tử tương đối tính phải là PT Dirac 𝛾 𝜇 𝑖ℏ𝜕𝜇 − 𝑒 𝑐 𝐴 𝜇 Ψ = 𝑚𝑐Ψ
  • 97.
    CH, ĐĐL vàCHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 97
  • 98.
    CH, ĐĐL vàCHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 98 PT Pauli
  • 99.
    CH, ĐĐL vàCHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 99 𝛼 = 𝑒2 4𝜋𝜀0ℏ𝑐
  • 100.
    CH, ĐĐL vàCHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 100 giải gần đúng PT Dirac Walter Gordon giải chính xác PT Dirac
  • 101.
    CH, ĐĐL vàCHLT tương đối tính 3. Cơ học lượng tử tương đối tính Dai-Nam Le 22/02/2019 101 LT Bohr LT Sommerfeld LT Schrodinger LT Darwin LT Dirac 1s1/2 -13,60569253 eV -13,60587366 eV -13,60569253 eV -13,60587366 eV -13,60587366 eV 2s1/2 -03,40142313 eV -03,40147974 eV -03,40142313 eV -03,40147974 eV -03,40147974 eV 2p1/2 -03,40143445 eV 2p3/2 -03,40143445 eV -03,40143445 eV 3s1/2 -01,51174361 eV -01,51176374 eV -01,51174361 eV -01,51176374 eV -01,51176374 eV 3p1/2 -01,51175032 eV 3p3/2 -01,51175032 eV -01,51175032 eV 3d3/2 -01,51174585 eV 3d5/2 -01,51174585 eV -01,51174585 eV
  • 102.
    Những hệ quảcủa Lý thuyết tương đối Quá trình ra đời Lý thuyết tương đối Những hệ quả của Lý thuyết tương đối hẹp Cơ học, Điện động lực học và Cơ học lượng tử tương đối tính Hai tiên đề của Einstein và phép biến đổi Lorentz Không gian Minkowski và giản đồ Minkowski 22/02/2019Dai-Nam Le 102 Lý thuyết tương đối và hệ quả
  • 103.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 103 1. Giãn nở thời gian 1 s 1 s
  • 104.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 104 1. Giãn nở thời gian
  • 105.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 105 1. Giãn nở thời gian > 1 s 1 s
  • 106.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 106 1. Giãn nở thời gian Theo định nghĩa thời gian riêng 𝑐𝑑𝜏 2 = 𝑐𝑑𝑡 2 − 𝑑𝑟 2 < 𝑐𝑑𝑡 2 ⇒ 𝑑𝑡 > 𝑑𝜏 Giãn nở thời gian Ở phần động học, ta đã có 𝑑𝜏 𝑑𝑡 = 1 𝛾 𝑢 ⟹ Δ𝑡 = 𝛾 Δ𝜏
  • 107.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 107 2. Co ngắn chiều dài Lorentz – Fitzgerald Thước 1 m
  • 108.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 108 2. Co ngắn chiều dài Lorentz – Fitzgerald Thước 1 m 1 m
  • 109.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 109 2. Co ngắn chiều dài Lorentz – Fitzgerald Thước 1 m Thời gian dài hơn của c = const Ngắn hơn 1 m !
  • 110.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 110 2. Co ngắn chiều dài Lorentz – Fitzgerald ct O x AB x’ ct’ 1 m
  • 111.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 111 2. Co ngắn chiều dài Lorentz – Fitzgerald ct O x AB x’ ct’ < 1 m
  • 112.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 112 2. Co ngắn chiều dài Lorentz – Fitzgerald Theo định nghĩa của chiều dài riêng − 𝑑𝑙 2 = 𝑐𝑑𝑡 2 − 𝑑𝑟 2 ⇒ 𝑑𝑙 < 𝑑𝑟 Þ co ngắn chiều dài Từ phép biến đổi Lorentz, ta có 𝑑𝑙 = 𝛾 𝑥 + 𝑑𝑟 − 𝑥 = 𝛾𝑑𝑟 ⟹ 𝑑𝑟 = 𝑑𝑙 𝛾
  • 113.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 113 2. Co ngắn chiều dài Lorentz – Fitzgerald Mọi người nhìn Mr. Tompkin Mr. Tompkin nhìn mọi người
  • 114.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 114 3. Tính tương đối của “đồng thời”
  • 115.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 115 3. Tính tương đối của “đồng thời” Cùng lúc Không cùng lúc AB
  • 116.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 116 3. Tính tương đối của “đồng thời” ct O x AB x’ ct’ Cùng lúc Không cùng lúc “Đồng thời” có tính tương đối
  • 117.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 117 4. Quan hệ nhân quả Ying đá gãy bút! Ying đá ? Bút gãy ?
  • 118.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 118 4. Quan hệ nhân quả ct O x x’ ct’ Ying đá gãy bút!
  • 119.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 119 4. Quan hệ nhân quả ct O x x’ ct’ Ying đá gãy bút!
  • 120.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 120 4. Quan hệ nhân quả Nguyên nhân  Kết quả : thông tin được truyền với vận tốc 𝑢 < 𝑐 ∆𝑡 = ∆𝑥 𝑢 ∆𝑡′ = 𝛾 ∆𝑡 − 𝑉 𝑐2 ∆𝑥 = 𝛾 1 − 𝑉𝑢 𝑐2 ∆𝑡 ⟹ ∆𝑡′ 𝑣à ∆𝑡 𝑐ù𝑛𝑔 𝑑ấ𝑢 Tính nhân quả như nhau trong mọi hệ quy chiếu quán tính.
  • 121.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 121 5. Nghịch lí anh em sinh đôi Paul Langevin
  • 122.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 122 5. Nghịch lí anh em sinh đôi ct O x Tính toán của 10 năm V = 0.6 c 4 năm 4 năm Trẻ hơn
  • 123.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 123 5. Nghịch lí anh em sinh đôi ct O x Tính toán của 3.2 năm V = 0.6 c 4 năm 4 năm 3.2 năm Trẻ hơn
  • 124.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 124 5. Nghịch lí anh em sinh đôi Max von Laue ct O x Bị mất Phá vỡ đối xứng
  • 125.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 125 6. Định lí cộng vận tốc Tên lửa: 𝑉 Đầu đạn: 𝑢′ (so với tên lửa) Vận tốc của đầu đạn đối với cây cầu?
  • 126.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 126 6. Định lí cộng vận tốc 𝒖 = 𝒖′ + 𝑽 Liệu nó còn đúng???
  • 127.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 127 6. Định lí cộng vận tốc ct’ O x’ 𝑢′ 𝑡′ + 𝑉𝑡′
  • 128.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 128 6. Định lí cộng vận tốc ct’ O x’ ct x
  • 129.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 129 8. Định lí cộng vận tốc 𝒖 ≠ 𝒖′ + 𝑽  Từ phép biến đổi Lorentz của 𝑐𝑡, 𝑥, 𝑦, 𝑧 → 𝑐𝑡′, 𝑥′, 𝑦′, 𝑧′ Kết hợp 𝑢 = 𝑑 𝑟 𝑑𝑡 𝑣à 𝑢′ = 𝑑𝑟′ 𝑑𝑡  Từ phép biến đổi Lorentz của 𝑢 𝜇 → 𝑢′ 𝜇
  • 130.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 130 8. Định lí cộng vận tốc 𝒖 ≠ 𝒖′ + 𝑽  Ta có định lí cộng vận tốc 𝑢1 = 𝑢′1 + 𝑉 1 + 𝑢′1 𝑉 𝑐 2 𝑢2 = 𝑢′2 𝛾 1 + 𝑢′1 𝑉 𝑐 2 𝑢3 = 𝑢′3 𝛾 1 + 𝑢′1 𝑉 𝑐 2
  • 131.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 131 8. Định lí cộng vận tốc Chứng minh định lí cộng vận tốc 𝑢1 = 𝑢′1 + 𝑉 1 + 𝑢′1 𝑉 𝑐 2 𝑢2 = 𝑢′2 𝛾 1 + 𝑢′1 𝑉 𝑐 2 𝑢3 = 𝑢′3 𝛾 1 + 𝑢′1 𝑉 𝑐 2 bằng cả hai cách.
  • 132.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 132 8. Định lí cộng vận tốc Sử dụng định lí cộng vận tốc để  Giải thích thí nghiệm của Fizeau về vận tốc ánh sáng trong chất lỏng chuyển động 𝑢 = 𝑐 𝑛 + 1 − 1 𝑛2 𝑣  Xây dụng công thức quang sai cho ánh sáng tan 𝜃 = sin 𝜃′ 𝛾 cos 𝜃′ + 𝑉 𝑐
  • 133.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 133 7. Sự thay đổi khối lượng  Khối lượng tương đối 𝑚 = 𝛾𝑚0 = 𝑚0 1 − 𝑢2 𝑐2 𝑢 𝑐 𝑚 𝑚0
  • 134.
    Những hệ quảcủa Lý thuyết tương đối 22/02/2019Dai-Nam Le 134 8. Mối quan hệ giữa khối lượng và năng lượng  Năng lượng 𝐸 = 𝑚𝑐2  Độ biến thiên năng lượng ∆𝐸 = ∆𝑚 𝑐2 Độ hụt khối Năng lượng phản ứng
  • 135.
    Dai-Nam Le 22/02/2019135 Thank You!
  • 136.
    Cấu trúc đềthi giữa kì 22/02/2019Dai-Nam Le 136 Điểm giữa kì chiếm 20% Đề thi gồm 04 câu bài tập 1. Lí thuyết cổ điển + tương đối 4 điểm 2. Phép biến đổi Lorentz và hệ quả 3 điểm 3. Động học tương đối tính 2 điểm 4. Câu hỏi phân loại 1 điểm
  • 137.
    Tìm hiểu thêm 22/02/2019Dai-NamLe 137 Bài toán phân rã và va chạm Rã 2 hạt 𝐴 → 𝐵 + 𝐶 HQC phòng thí nghiệm A B C
  • 138.
    Tìm hiểu thêm 22/02/2019Dai-NamLe 138 Bài toán phân rã và va chạm Rã 2 hạt 𝐴 → 𝐵 + 𝐶 HQC khối tâm A B C
  • 139.
    𝐴 → 𝐵+ 𝐶 VD: 𝜋0 → 𝛾 + 𝛾 (𝑏𝑟𝑎𝑛𝑐ℎ𝑖𝑛𝑔 𝑟𝑎𝑡𝑖𝑜 = 0.98823) Tìm hiểu thêm 22/02/2019Dai-Nam Le 139 Bài toán phân rã và va chạm Rã 2 hạt
  • 140.
    VD: 𝜋0 →𝛾 + 𝛾 (𝑏𝑟𝑎𝑛𝑐ℎ𝑖𝑛𝑔 𝑟𝑎𝑡𝑖𝑜 = 0.98823) Tìm hiểu thêm 22/02/2019Dai-Nam Le 140 Bài toán phân rã và va chạm Rã 2 hạt
  • 141.
    Tìm hiểu thêm 22/02/2019Dai-NamLe 141 Bài toán trường xuyên tâm trong Lí thuyết tương đối
  • 142.
    Tìm hiểu thêm 22/02/2019Dai-NamLe 142 Giới hạn ứng dụng của Lí thuyết tương đối