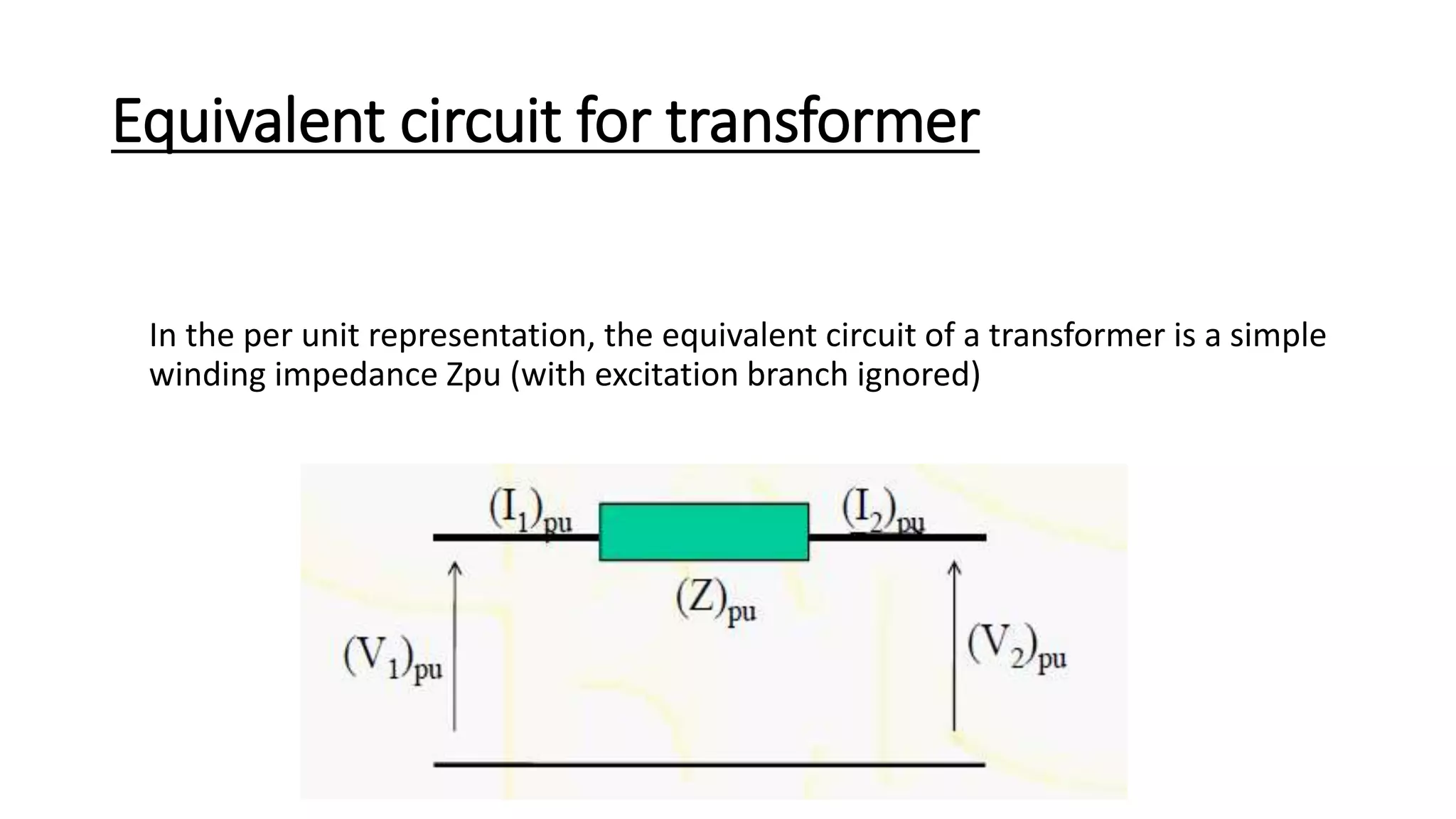
The per-unit system defines quantities as ratios of their actual value to a base or reference value. This makes quantities dimensionless and allows easy comparison between equipment of different ratings. Base values are chosen, typically a machine's rating, to simplify calculations. Common bases are voltage, power, and their related current and impedance values, keeping the relationships between quantities. Per-unit notation expresses values as fractions of the reference value and has advantages like dealing with values near unity rather than a wide range.

2. Per Unit System
The per-unit value of any quantity is defined as the ratio of actual
value in any unit to the base or reference value in the same unit. Any
quantity is converted into per unit quantity by dividing the numeral
value by the chosen base value of the same dimension. The per-unit
value is dimensionless.

3. Per Unit System
Any value can be taken as the Base Value. However, it is chosen to
make computation easy. It is usually taken equal to the rating of a
machine/transformer in the power circuit. Power equipment
impedance ratings are usually given in p.u. (expressed in %) based on
their rated voltage and VA.

4. Basic Units
The 4 basic electrical quantities are:
• Voltage V (volt)
• Current I (amp)
• Impedance Z (ohm)
• Power S (VA)
For single-phase circuits,
• V(volt) = Z(ohm) × I(amp);
• S (VA) = V(volt) × I(amp)*

5. Per unit notation
In per unit notation, the physical quantity is expressed as a fraction of the reference
value, i.e.
per unit value = actual value/base value in the same unit.
e.g. V(in per unit) = V(in kV)/V base (in kV)
where the base value is a reference value for magnitude.

6. Base Quantities
In per unit notation we would like to keep
the basic relations: Vpu = Zpu Ipu; Spu = Vpu Ipu*
Hence the base quantities should be chosen such that
Base voltage (VB) =
base impedance (ZB) × base current (IB)
Base power (SB) =
base voltage (VB) × base current(IB)

7. Base Quantities
Thus only two of the base quantities can be arbitrarily chosen, the
other two will follow directly.
It is common practice to specify
base power (SB) and base voltage (VB)
Then it follows
base current IB = SB/VB
base impedance ZB = VB/IB =V𝐵2/SB

8. Percentage Values
An equivalent way to express the per unit value is the percentage value where
Percentage value = per unit value × 100%
However, percentage values are not so convenient to use since
Vpercent ≠ Zpercent × Ipercent

9. Base Value for 3-phase systems
For 3-phase systems it is common practice to describe system
operation with:
total 3-phase power S = 𝑆3−ɸ
line voltage V = Vline
line current I = Iline
equivalent impedance/phase Z = Zph
with (in magnitude)
V = √3ZI; S = √3VI.

10. Base Value for 3-phase systems
Hence if base values are chosen for:
total 3-phase power SB
line voltage VB
Then
base line current
IB = SB/ √3VB
base impedance
ZB = VB/ √3IB = V𝐵2/SB

11. Equivalent circuit for transformer
In the per unit representation, the equivalent circuit of a transformer is a simple
winding impedance Zpu (with excitation branch ignored)

12. Advantages of Per Unit System
• Normally we are dealing with numerics near unity rather than over a wide range.
• Provides a more meaningful comparison of parameters of machines with
different ratings.
• As the per unit values of parameters of a machine of a given design normally falls
within a certain range, a typical value can be used if such parameters are not
provided.