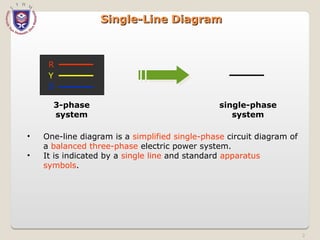
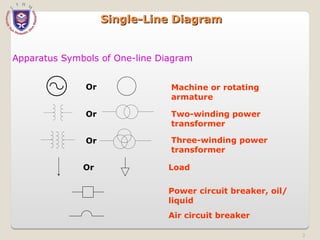
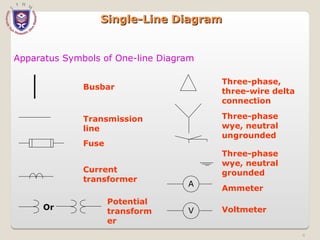
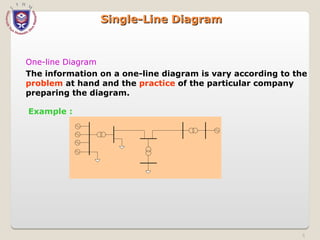
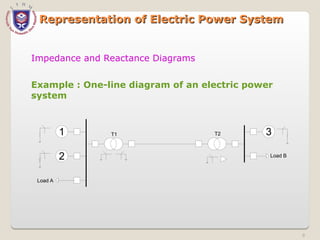
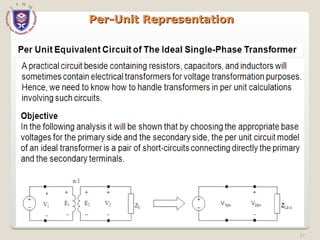
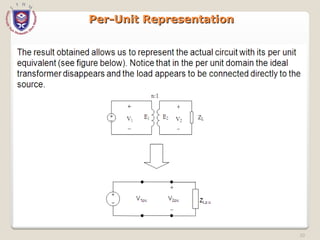
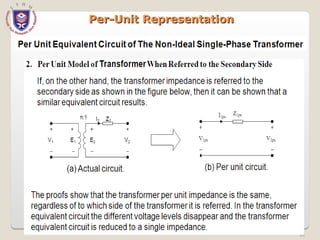
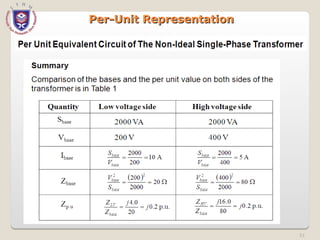
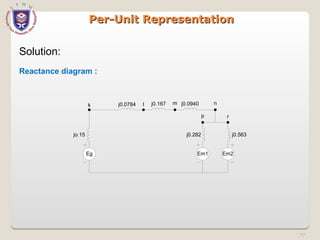
The document discusses the concept and representation of a single-line diagram in three-phase electric power systems, which simplifies complex circuits into standardized symbols. It explains the importance of impedance and reactance diagrams for analyzing system performance under load and during faults. The guide also introduces the per-unit system for easier calculations across different voltage levels, outlining its benefits and providing examples for clarity.