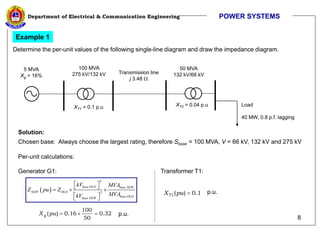
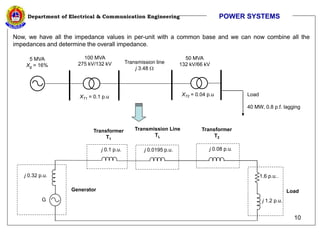
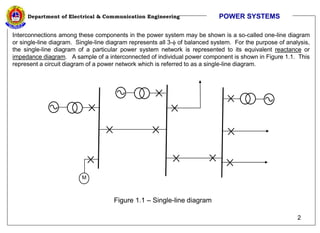
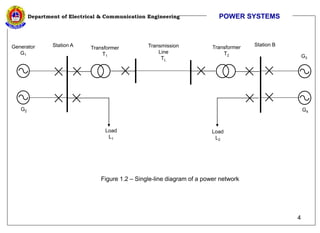
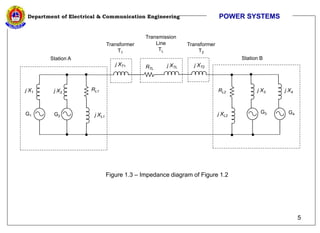
The document discusses per unit calculations in power systems. It defines per unit quantities as actual quantities normalized by a base quantity. Common base quantities used are voltage (Vbase), apparent power (Sbase), and impedance (Zbase). The document provides formulas for calculating base impedance and converting impedances to different bases. It includes an example of calculating the per unit impedances of components in a sample power system diagram and drawing the equivalent impedance diagram.


![7
Department of Electrical & Communication Engineering
Combining (i) and (ii) yields,
base
base
base
base
V
S
V
Z
3
3
base
base
base
MVA
kV
Z
2
where kVbase and MVAbase are 3- qualtities
(ii) Changing base impedance (Znew]
Sometimes the parameters for two elements in the same circuit (network) are quoted in per-unit on a different
base. The changing base impedance is given as,
2
2
base OLD base NEW
NEW OLD
base OLD
base NEW
kV MVA
Z pu Z
MVA
kV
POWER SYSTEMS](https://image.slidesharecdn.com/chapter1perunitaugust2011-240314160808-12082ddc/85/chapter_1_per_unit_power-system_august_2011-ppt-7-320.jpg)