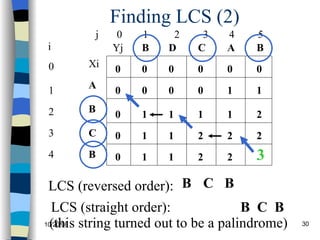
The document discusses dynamic programming and its application to solving the longest common subsequence (LCS) problem. It presents the LCS algorithm, which uses dynamic programming to find the length and sequence of the longest subsequence common to two strings X and Y in O(mn) time, where m and n are the lengths of X and Y, respectively. It provides an example running the LCS algorithm on strings X="ABCB" and Y="BDCAB" to determine their longest common subsequence is "BCB".

1. CS 332 - Algorithms Dynamic programming Longest Common Subsequence

2. Dynamic programming It is used, when the solution can be recursively described in terms of solutions to subproblems ( optimal substructure ) Algorithm finds solutions to subproblems and stores them in memory for later use More efficient than “ brute-force methods ”, which solve the same subproblems over and over again

3. Longest Common Subsequence (LCS) Application: comparison of two DNA strings Ex: X= {A B C B D A B }, Y= {B D C A B A} Longest Common Subsequence: X = A B C B D A B Y = B D C A B A Brute force algorithm would compare each subsequence of X with the symbols in Y

4. LCS Algorithm if |X| = m, |Y| = n, then there are 2 m subsequences of x; we must compare each with Y (n comparisons) So the running time of the brute-force algorithm is O(n 2 m ) Notice that the LCS problem has optimal substructure : solutions of subproblems are parts of the final solution. Subproblems: “find LCS of pairs of prefixes of X and Y”

5. LCS Algorithm First we’ll find the length of LCS. Later we’ll modify the algorithm to find LCS itself. Define X i , Y j to be the prefixes of X and Y of length i and j respectively Define c[i,j] to be the length of LCS of X i and Y j Then the length of LCS of X and Y will be c[m,n]

6. LCS recursive solution We start with i = j = 0 (empty substrings of x and y) Since X 0 and Y 0 are empty strings, their LCS is always empty (i.e. c[0,0] = 0 ) LCS of empty string and any other string is empty, so for every i and j: c[0, j] = c[i,0] = 0

7. LCS recursive solution When we calculate c[i,j], we consider two cases: First case: x[i]=y[j] : one more symbol in strings X and Y matches, so the length of LCS X i and Y j equals to the length of LCS of smaller strings X i-1 and Y i-1 , plus 1

8. LCS recursive solution Second case: x[i] != y[j] As symbols don’t match, our solution is not improved, and the length of LCS(X i , Y j ) is the same as before (i.e. maximum of LCS(X i , Y j-1 ) and LCS(X i-1 ,Y j ) Why not just take the length of LCS(X i-1 , Y j-1 ) ?

9. LCS Length Algorithm LCS-Length(X, Y) 1. m = length(X) // get the # of symbols in X 2. n = length(Y) // get the # of symbols in Y 3. for i = 1 to m c[i,0] = 0 // special case: Y 0 4. for j = 1 to n c[0,j] = 0 // special case: X 0 5. for i = 1 to m // for all X i 6. for j = 1 to n // for all Y j 7. if ( X i == Y j ) 8. c[i,j] = c[i-1,j-1] + 1 9. else c[i,j] = max( c[i-1,j], c[i,j-1] ) 10. return c

10. LCS Example We’ll see how LCS algorithm works on the following example: X = ABCB Y = BDCAB LCS(X, Y) = BCB X = A B C B Y = B D C A B What is the Longest Common Subsequence of X and Y?

11. LCS Example (0) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D X = ABCB; m = |X| = 4 Y = BDCAB; n = |Y| = 5 Allocate array c[5,4] ABCB BDCAB

12. LCS Example (1) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 for i = 1 to m c[i,0] = 0 for j = 1 to n c[0,j] = 0 ABCB BDCAB

13. LCS Example (2) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 0 A BCB B DCAB

14. LCS Example (3) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 0 0 0 A BCB B DC AB

15. LCS Example (4) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 0 0 0 1 A BCB BDC A B

16. LCS Example (5) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 0 0 0 1 1 A BCB BDCA B

17. LCS Example (6) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 0 0 1 0 1 1 A B CB B DCAB

18. LCS Example (7) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 1 0 0 0 1 1 1 1 1 A B CB B DCA B

19. LCS Example (8) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 1 0 0 0 1 1 1 1 1 2 A B CB BDCA B

20. LCS Example (10) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 1 0 0 0 1 2 1 1 1 1 1 1 AB C B BD CAB

21. LCS Example (11) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 1 0 0 0 1 1 2 1 1 1 1 1 2 AB C B BD C AB

22. LCS Example (12) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 1 0 0 0 1 1 2 1 1 1 1 2 1 2 2 AB C B BDC AB

23. LCS Example (13) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 1 0 0 0 1 1 2 1 1 1 1 2 1 2 2 1 ABC B B DCAB

24. LCS Example (14) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 1 0 0 0 1 1 2 1 1 1 1 2 1 2 2 1 1 2 2 ABC B B DCA B

25. LCS Example (15) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C B Yj B B A C D 0 0 0 0 0 0 0 0 0 0 if ( X i == Y j ) c[i,j] = c[i-1,j-1] + 1 else c[i,j] = max( c[i-1,j], c[i,j-1] ) 1 0 0 0 1 1 2 1 1 1 1 2 1 2 2 1 1 2 2 3 ABC B BDCA B

26. LCS Algorithm Running Time LCS algorithm calculates the values of each entry of the array c[m,n] So what is the running time? O(m*n) since each c[i,j] is calculated in constant time, and there are m*n elements in the array

27. How to find actual LCS So far, we have just found the length of LCS, but not LCS itself. We want to modify this algorithm to make it output Longest Common Subsequence of X and Y Each c[i,j] depends on c[i-1,j] and c[i,j-1] or c[i-1, j-1] For each c[i,j] we can say how it was acquired: 2 2 3 2 For example, here c[i,j] = c[i-1,j-1] +1 = 2+1=3

28. How to find actual LCS - continued Remember that So we can start from c[m,n] and go backwards Whenever c[i,j] = c[i-1, j-1]+1 , remember x[i] (because x[i] is a part of LCS) When i=0 or j=0 (i.e. we reached the beginning), output remembered letters in reverse order

29. Finding LCS j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C Yj B B A C D 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 2 1 1 1 1 2 1 2 2 1 1 2 2 3 B

30. Finding LCS (2) j 0 1 2 3 4 5 0 1 2 3 4 i Xi A B C Yj B B A C D 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 2 1 1 1 1 2 1 2 2 1 1 2 2 3 B B C B LCS (reversed order): LCS (straight order): B C B (this string turned out to be a palindrome)

31. Knapsack problem Given some items, pack the knapsack to get the maximum total value. Each item has some weight and some value. Total weight that we can carry is no more than some fixed number W. So we must consider weights of items as well as their value. Item # Weight Value 1 1 8 2 3 6 3 5 5

32. Knapsack problem There are two versions of the problem: (1) “0-1 knapsack problem” and (2) “Fractional knapsack problem” (1) Items are indivisible; you either take an item or not. Solved with dynamic programming (2) Items are divisible: you can take any fraction of an item. Solved with a greedy algorithm .