This document presents an overview of optimization algorithms on Riemannian manifolds. It begins by introducing concepts such as vector transport and retraction mappings that are used to generalize algorithms from Euclidean spaces to manifolds. It then summarizes several classical optimization methods including gradient descent, conjugate gradient, and variants of quasi-Newton methods adapted to the Riemannian setting using these geometric concepts. The convergence of the Fletcher-Reeves method is analyzed under standard assumptions on the objective function. Overall, the document provides a conceptual and mathematical foundation for optimization on manifolds.

1. 2016 3 10

2. 1
2
3
4
5
( ) 2016 3 10 1 / 67

3. 1
2
3
4
5
( ) 2016 3 10 2 / 67

4. Rn
1.1 (Rn
)
minimize f(x),
subject to x ∈ Rn
.
1.1 Rn
1: x0 ∈ Rn
2: for k = 0, 1, 2, . . . do
3: ηk ∈ Rn
tk > 0
4: xk+1 xk+1 := xk + tkηk
5: end for
( ) 2016 3 10 3 / 67

5. Rn
( ) 2016 3 10 4 / 67

6. Rn
ηk
∇f, ∇2
f f
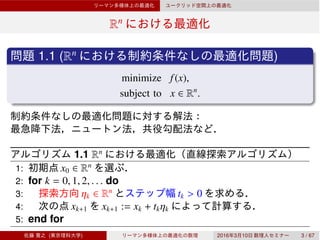
ηk := −∇f(xk).
ηk η ∈ Rn
∇2
f(xk)[η] = −∇f(xk)
⎧
⎪⎪⎨
⎪⎪⎩
η0 := −∇f(x0),
ηk+1 := −∇f(xk+1) + βk+1ηk, k ≥ 0.
βk
( ) 2016 3 10 5 / 67

7. A n
1.2
minimize f(x) =
xT
Ax
xTx
,
subject to x ∈ Rn
− {0} .
f(x)
A
x f ⇔ Ax =
xT
Ax
∥x∥2
x
⇒ x η η = x.
→
( ) 2016 3 10 6 / 67

8. 1.2 Rn
1.3
minimize f(x) = xT
Ax,
subject to x ∈ Rn
, xT
x = 1.
n − 1 Sn−1
1.4
minimize f(x) = xT
Ax,
subject to x ∈ Sn−1
.
( ) 2016 3 10 7 / 67

9. 1.1
M M
Ui Ui Rn
ϕi : Ui → ϕi(Ui)
i
Ui = M,
Ui ∩ Uj ∅
ϕi ◦ ϕ−1
j |ϕj(Ui∩Uj) : ϕj(Ui ∩ Uj) → ϕi(Ui ∩ Uj)
C∞
M Rn
M
R3
M
M
( ) 2016 3 10 8 / 67

10. p ≤ n
n − 1 Sn−1
= x ∈ Rn
| xT
x = 1 ⊂ Rn
n O(n) = X ∈ Rn×n
| XT
X = In ⊂ Rn×n
St(p, n) = Y ∈ Rn×p
| YT
Y = Ip ⊂ Rn×p
n − 1 RPn−1
= l : Rn
Grass(p, n) = W : Rn
p
( ) 2016 3 10 9 / 67

11. Rn
M
ηk M xk .
Rn
xk+1 := xk + tkηk
M
→ γ(0) = xk, ˙γ(0) = ηk M γ xk+1
R : TM → M Rx := R|TxM
xk+1 := Rxk
(tkηk), Rxk
: Txk
M → M.
( ) 2016 3 10 10 / 67

12. M R ( )
1.2
x0 ∈ M .
for k = 0, 1, 2, . . . do
ηk ∈ Txk
M tk > 0 .
xk+1 xk+1 := Rxk
(tkηk) .
end for
ηk tk
( ) 2016 3 10 11 / 67

13. ( ) 2016 3 10 12 / 67

14. M
ηk := − grad f(xk) grad M
⎧
⎪⎪⎨
⎪⎪⎩
η0 := − grad f(x0),
(?) ηk+1 := − grad f(xk+1) + βk+1ηk, k ≥ 0.
grad f ∇f
grad f(xk+1) ∈ Txk+1
M ηk ∈ Txk
M
( ) 2016 3 10 13 / 67

15. 1
2
3
4
5
( ) 2016 3 10 14 / 67

16. x ∈ M TxM
x ∈ M
2
M γ ˙γ(0)
f : M → R ˙γ(0)f =
d
dt
f(γ(t))|t=0
M ˙γ(0)
d
dt
γ(t)|t=0
Sn−1
:= {x ∈ Rn
| xT
x = 1}
TxSn−1
= {ξ ∈ Rn
| ξT
x = 0}.
( ) 2016 3 10 15 / 67

17. g
x ∈ M TxM gx x
Sn−1
Rn
Rn
⟨a, b⟩ = aT
b, a, b ∈ Rn
gx(ξ, η) = ξT
η, ξ, η ∈ TxSn−1
g TxM
gx(ξ, η) ⟨ξ, η⟩x
( ) 2016 3 10 16 / 67

18. f grad f(x)
M f x grad f(x) TxM
D f(x)[ξ] = gx(grad f(x), ξ), ξ ∈ TxM
Sn−1
f(x) = xT
Ax A
f Rn ¯f
¯f(x) = xT
Ax, x ∈ Rn
.
¯f Rn
∇¯f(x) = 2Ax
ξ ∈ TxSn−1
Df(x)[ξ] = 2xT
Aξ = 2xT
A(In − xxT
)ξ = gx(2(In − xxT
)Ax, ξ)
grad f(x) = 2 In − xxT
Ax.
( ) 2016 3 10 17 / 67

19. R : TM → M
R [Absil et al., 2008]
2.1
R : TM → M R
Rx := R|TxM R TxM
Rx(0x) = x, ∀x ∈ M. 0x TxM
DRx(0x)[ξ] = ξ, ∀x ∈ M, ξ ∈ TxM.
x ∈ M, ξ ∈ TxM γ(t) = Rx(tξ)
γ(0) = Rx(0) = x γ(t) x
˙γ(0) = DRx(0)[ξ] = ξ γ(t) ξ
( ) 2016 3 10 18 / 67

20. Sn−1
Rx(ξ) =
x + ξ
∥x + ξ∥
, x ∈ Sn−1
, ξ ∈ TxSn−1
R
( ) 2016 3 10 19 / 67

21. 1
2
3
4
5
( ) 2016 3 10 20 / 67

22. Rn
3.1 Rn
1: x0 ∈ Rn
.
2: η0 := −∇f(x0).
3: while ∇f(xk) 0 do
4: αk xk+1 := xk + αkηk .
5: βk+1
ηk+1 := −∇f(xk+1)+βk+1ηk (1)
6: k := k + 1.
7: end while
M
(1) +
grad f(x ) ∈ T M, η ∈ T M →( ) 2016 3 10 21 / 67

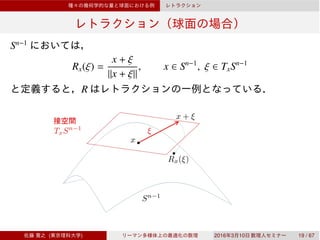
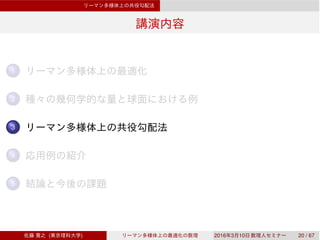
23. Vector transport
Vector transport
M vector transport T TM ⊕ TM → TM
x ∈ M
[Absil et al., 2008]
1 R π(Tηx
(ξx)) = R(ηx).
π(Tηx
(ξx)) Tηx
(ξx)
2 T0x
(ξx) = ξx, ξx ∈ TxM.
3 Tηx
(aξx + bζx) = aTηx
(ξx) + bTηx
(ζx), a, b ∈ R.
vector transport
( ) 2016 3 10 22 / 67

24. Vector transport
Vector transport
M R
T R
ηx
(ξx) := DRx(ηx)[ξx]
T R
vector transport
T T R
( ) 2016 3 10 23 / 67

25. Vector transport
Vector transport
3.1 M
1: x0 ∈ M .
2: η0 := − grad f(x0).
3: while grad f(xk) 0 do
4: αk xk+1 := Rxk
(αkηk) .
5: βk+1 ηk+1 := − grad f(xk+1) + βk+1Tαkηk
(ηk)
6: k := k + 1.
7: end while
αk βk
( ) 2016 3 10 24 / 67

26. 0 < c1 < c2 < 1
Rn
xk ∈ Rn
ηk ∇f(xk)T
ηk < 0
f(xk + αkηk) ≤ f(xk) + c1αk∇f(xk)T
ηk, (2)
∇f(xk + αkηk)T
ηk ≥ c2∇f(xk)T
ηk, (3)
|∇f(xk + αkηk)T
ηk| ≤ c2|∇f(xk)T
ηk|. (4)
(2)
(2) (3)
(2) (4)
( ) 2016 3 10 25 / 67

27. φ(α) := f(xk + αηk) (2), (3), (4)
φ(αk) ≤ φ(0) + c1αkφ′
(0), (5)
φ′
(αk) ≥ c2φ′
(0), (6)
|φ′
(αk)| ≤ c2|φ′
(0)| (7)
(5)
(5) (6)
(5) (7)
M φ(α) := f(Rxk
(αηk))
(5), (6), (7)
( ) 2016 3 10 26 / 67

28. 0 < c1 < c2 < 1
M xk ∈ M ηk
⟨grad f(xk), ηk⟩xk
< 0
f(Rxk
(αkηk)) ≤ f(xk) + c1αk⟨gradf(xk), ηk⟩xk
, (8)
⟨grad f(Rxk
(αkηk)), DRxk
(αkηk)[ηk]⟩xk
≥ c2⟨grad f(xk), ηk⟩xk
, (9)
|⟨grad f(Rxk
(αkηk)), DRxk
(αkηk)[ηk]⟩xk
| ≤ c2|⟨grad f(xk), ηk⟩xk
|. (10)
[Absil et al., 2008] (8)
[Sato, 2015] (8) (9)
[Ring & Wirth, 2012] (8) (10)
DRxk
(αkηk)[ηk] = T R
αkηk
(ηk)
( ) 2016 3 10 27 / 67

29. βk
Rn
βk
gk := ∇f(xk), yk := gk+1 − gk
βHS
k+1 =
gT
k+1yk
ηT
k yk
. [Hestenes & Stiefel, 1952]
βFR
k+1 =
∥gk+1∥2
∥gk∥2
. [Fletcher & Reeves, 1964]
βPRP
k+1 =
gT
k+1yk
∥gk∥2
. [Polak, Ribi`ere, Polyak, 1969]
βCD
k+1 =
∥gk+1∥2
−ηT
k gk
. [Fletcher, 1987]
βLS
k+1 =
gT
k+1yk
−ηT
k gk
. [Liu & Storey, 1991]
βDY
k+1 =
∥gk+1∥2
ηT
k yk
. [Dai & Yuan, 1999]
( ) 2016 3 10 28 / 67

30. βk
βk
gk := ∇f(xk), yk := gk+1 − gk
Fletcher–Reeves: Rn
βFR
k+1 =
∥gk+1∥2
∥gk∥2
.
→ M
βk+1 =
⟨grad f(xk+1), grad f(xk+1)⟩xk+1
⟨grad f(xk), grad f(xk)⟩xk
Dai–Yuan: Rn
βDY
k+1 =
∥gk+1∥2
ηT
k yk
.
→ M
(?) βk+1 :=
⟨grad f(xk+1), grad f(xk+1)⟩xk+1
⟨ηk, yk⟩xk
yk = grad f(xk+1) − Tαkηk
(grad f(xk))?
( ) 2016 3 10 29 / 67

31. Fletcher–Reeves
Scaled vector transport
Rn
vector transport T
∥Tαk−1ηk−1
(ηk−1)∥xk
≤ ∥ηk−1∥xk−1
Vector transport
Vector transport T R
scaled vector transport T 0
[Sato & Iwai, 2015]
T 0
η (ξ) =
∥ξ∥x
∥T R
η (ξ)∥Rx(η)
T R
η (ξ), ξ, η ∈ TxM.
( ) 2016 3 10 30 / 67

32. Fletcher–Reeves
Scaled vector transport Fletcher–Reeves
3.2 Fletcher–Reeves
1: x0 ∈ M
2: η0 := − grad f(x0).
3: while grad f(xk) 0 do
4: αk
xk+1 := Rxk
(αkηk)
5: βk+1 :=
⟨grad f(xk+1), grad f(xk+1)⟩xk+1
⟨grad f(xk), grad f(xk)⟩xk
ηk+1 := − grad f(xk+1) + βk+1T (k)
αkηk
(ηk)
6: k := k + 1.
7: end while
T (k)
αkηk
(ηk) :=
⎧
⎪⎪⎨
⎪⎪⎩
T R
αkηk
(ηk), if ∥T R
αkηk
(ηk)∥xk+1
≤ ∥ηk∥xk
,
T 0
αkηk
(ηk), otherwise.
( ) 2016 3 10 31 / 67

33. Fletcher–Reeves
Fletcher–Reeves
3.1 (Sato & Iwai, 2015)
f C1
L > 0
|D(f ◦ Rx)(tη)[η] − D(f ◦ Rx)(0)[η]| ≤ Lt,
η ∈ TxM with ∥η∥x = 1, x ∈ M, t ≥ 0
3.2 {xk}
lim inf
k→∞
∥grad f(xk)∥xk
= 0
( ) 2016 3 10 32 / 67

34. Fletcher–Reeves
[Ring & Wirth, 2012]
k
∥T R
αk−1ηk−1
(ηk−1)∥xk
≤ ∥ηk−1∥xk−1
(11)
vector transport T R
[Sato & Iwai, 2015]
(11) (11) vector
transport scaled vector transport
( ) 2016 3 10 33 / 67

35. Fletcher–Reeves
(11)
n = 20, A = diag(1, . . . , 20) Sn−1
:= x ∈ Rn
| xT
x = 1
3.1
minimize f(x) = xT
Ax,
subject to x ∈ Sn−1
,
Sn−1
gx(ξx, ηx) := ξT
x Gxηx, ξx, ηx ∈ TxSn−1
,
Gx := diag(104
(x(1)
)2
+ 1, 1, 1, . . . , 1) x(1)
x 1
( ) 2016 3 10 34 / 67

36. Fletcher–Reeves
grad f(x) = 2 In −
G−1
x xxT
xTG−1
x x
G−1
x Ax.
Rx(ξ) =
x + ξ
(x + ξ)T(x + ξ)
, ξ ∈ TxSn−1
, x ∈ Sn−1
,
Vector transport:
T R
η (ξ) =
1
(x + η)T(x + η)
In −
(x + η)(x + η)T
(x + η)T(x + η)
ξ,
η, ξ ∈ TxSn−1
, x ∈ Sn−1
.
x∗ f(x∗) = 1
( ) 2016 3 10 35 / 67

37. Fletcher–Reeves
0 2 4 6 8 10
x 10
4
1.45
1.5
1.55
1.6
Iteration
f(xk)
( ) 2016 3 10 36 / 67

38. Fletcher–Reeves
0 2 4 6 8 10
x 10
4
0.6
0.65
0.7
0.75
0.8
0.85
Iteration
x
(1)
k
( ) 2016 3 10 37 / 67

39. Fletcher–Reeves
0 2 4 6 8 10
x 10
4
0
0.5
1
1.5
2
2.5
Iteration
||TR
αkηk
(ηk)||xk+1
/||ηk||xk
( ) 2016 3 10 38 / 67

40. Fletcher–Reeves
0 0.5 1 1.5 2
x 10
4
0.5
1
1.5
Iteration
x
k
(1)
Ratios
( ) 2016 3 10 39 / 67

41. Fletcher–Reeves
0 50 100 150 200
0
0.2
0.4
0.6
0.8
1
Iteration
x
(1)
k
( ) 2016 3 10 40 / 67

42. Fletcher–Reeves
0 50 100 150 200
10
−8
10
−6
10
−4
10
−2
10
0
10
2
Iteration
Distancetosolution
( ) 2016 3 10 41 / 67

43. Fletcher–Reeves
n = 100, A = diag(1, . . . , 100)/100
Sn−1
3.2
minimize f(x) = xT
Ax,
subject to x ∈ Sn−1
,
Sn−1
gx(ξx, ηx) := ξT
x ηx, ξx, ηx ∈ TxSn−1
,
( ) 2016 3 10 42 / 67

44. Fletcher–Reeves
grad f(x) = 2 I − xxT
Ax.
Rx(ξ) = 1 − ξTξx + ξ, ξ ∈ TxSn−1
, x ∈ Sn−1
,
Vector transport:
T R
η (ξ) = ξ −
ηT
ξ
1 − ηTη)
x,
η, ξ ∈ TxSn−1
with ∥η∥x, ∥ξ∥x < 1, x ∈ Sn−1
.
(2) ∥T R
η (ξ)∥Rx(η) > ∥ξ∥x.
( ) 2016 3 10 43 / 67

45. Fletcher–Reeves
0 50 100 150 200 250 300 350
10
−6
10
−4
10
−2
10
0
Iteration
Distancetosolution
既存手法
提案手法
( ) 2016 3 10 44 / 67

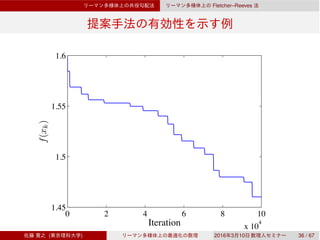
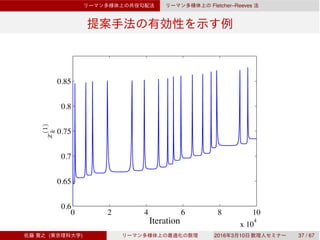
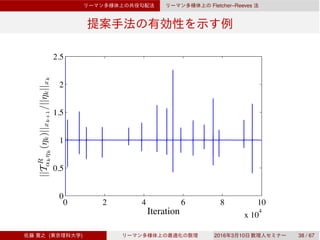
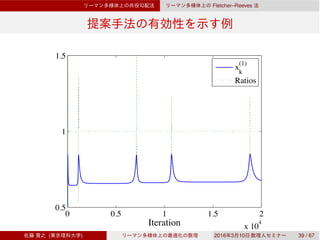
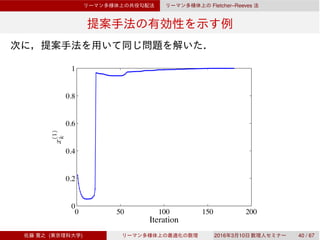
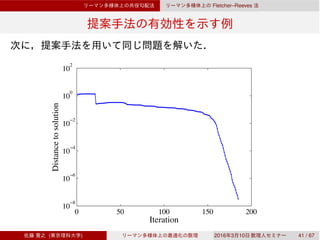
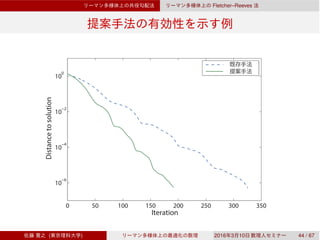
46. Dai–Yuan
Rn
Dai–Yuan
3.3 Rn
Dai–Yuan [Dai & Yuan, 1999]
1: x0 ∈ Rn
2: η0 := − grad f(x0).
3: while grad f(xk) 0 do
4: αk xk+1 :=
xk + αkηk
5:
βk+1 =
∥gk+1∥2
ηT
k yk
, ηk+1 := − grad f(xk+1) + βk+1ηk
gk = grad f(xk), yk = gk+1 − gk.
6: k := k + 1.
7: end while
( ) 2016 3 10 45 / 67

47. Dai–Yuan
Rn
Dai–Yuan
3.2
f L = {x ∈ Rn
| f(x) ≤ f(x1)} N
C1
L > 0
∥∇f(x) − ∇f(y)∥ ≤ L∥x − y∥, ∀x, y ∈ N
3.3 {xk}
lim inf
k→∞
∥grad f(xk)∥xk
= 0
( ) 2016 3 10 46 / 67

48. Dai–Yuan
Dai–Yuan
Rn
gk = ∇f(xk), yk = gk+1 − gk
βk+1 =
∥gk+1∥2
ηT
k yk
=
gT
k+1ηk+1
gT
k ηk
M gk = grad f(xk)
βk+1 =
⟨gk+1, ηk+1⟩xk+1
⟨gk, ηk⟩xk
ηk+1 βk+1
βk+1
( ) 2016 3 10 47 / 67

49. Dai–Yuan
Dai–Yuan
βk+1 =
⟨gk+1, ηk+1⟩xk+1
⟨gk, ηk⟩xk
=
⟨gk+1, −gk+1 + βk+1T (k)
αkηk
(ηk)⟩xk+1
⟨gk, ηk⟩xk
=
−∥gk+1∥2
+ βk+1⟨gk+1, T (k)
αkηk
(ηk)⟩xk+1
⟨gk, ηk⟩xk
.
βk+1 =
∥gk+1∥2
xk+1
⟨gk+1, T (k)
αkηk
(ηk)⟩xk+1
− ⟨gk, ηk⟩xk
.
( ) 2016 3 10 48 / 67

50. Dai–Yuan
Dai–Yuan
Rn
βk+1 =
gT
k+1ηk+1
gT
k ηk
=
∥gk+1∥2
ηT
k yk
, yk = gk+1 − gk.
M
βk+1 =
⟨gk+1, ηk+1⟩xk+1
⟨gk, ηk⟩xk
=
∥gk+1∥2
xk+1
⟨T (k)
αkηk
(ηk), yk⟩xk+1
.
yk = gk+1 −
⟨gk, ηk⟩xk
⟨T (k)
αkηk
(gk), T (k)
αkηk
(ηk)⟩xk+1
T (k)
αkηk
(gk).
( ) 2016 3 10 49 / 67

51. Dai–Yuan
Dai–Yuan
3.3 (Sato, 2015)
f C1
L > 0
|D(f ◦ Rx)(tη)[η] − D(f ◦ Rx)(0)[η]| ≤ Lt,
η ∈ TxM with ∥η∥x = 1, x ∈ M, t ≥ 0
{xk}
lim inf
k→∞
∥grad f(xk)∥xk
= 0
( ) 2016 3 10 50 / 67

52. Dai–Yuan
f(x) = xT
Ax, x ∈ Sn−1
.
Iteration
0 50 100 150 200 250 300 350
Normofthegradient
10-6
10-4
10-2
100
102
DY + wWolfe
DY + sWolfe
FR + wWolfe
FR + sWolfe
3.1: n = 100, A = diag(1, 2, . . . , n), x0 = 1n/
√
n.
( ) 2016 3 10 51 / 67

53. Dai–Yuan
f(x) = xT
Ax, x ∈ Sn−1
.
Iteration
0 200 400 600 800 1000
Normofthegradient
10-6
10-4
10-2
100
102
104
DY + wWolfe
DY + sWolfe
FR + wWolfe
FR + sWolfe
3.2: n = 500, A = diag(1, 2, . . . , n), x0 = 1n/
√
n.
( ) 2016 3 10 52 / 67

54. Dai–Yuan
f(x) = xT
Ax, x ∈ Sn−1
.
3.1: n = 100, A = diag(1, 2, . . . , n), x0 = 1n/
√
n.
PPPPPPMethod
Iterations Function Evals. Gradient Evals. Computational time
DY + wWolfe 149 210 206 0.0175
DY + sWolfe 90 288 244 0.0187
FR + wWolfe 318 619 577 0.0429
FR + sWolfe 91 293 258 0.0191
3.2: n = 500, A = diag(1, 2, . . . , n), x0 = 1n/
√
n.
PPPPPPMethod
Iterations Function Evals. Gradient Evals. Computational time
DY + wWolfe 340 373 367 0.0522
DY + sWolfe 232 657 467 0.0658
FR + wWolfe 960 1902 1757 0.1988
FR + sWolfe 300 723 529 0.0730
( ) 2016 3 10 53 / 67

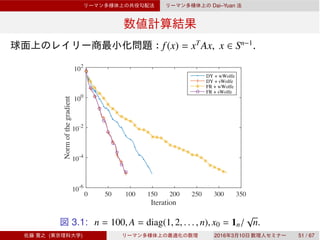
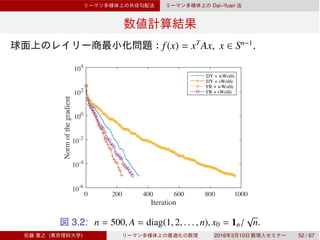
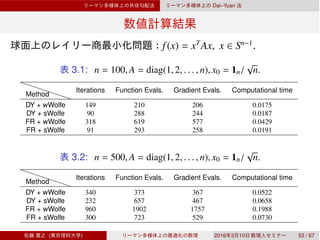
55. Rn
βk
βPRP
k+1 =
g⊤
k+1yk
∥gk∥2
, βHS
k+1 =
g⊤
k+1yk
d⊤
k yk
, βLS
k+1 =
g⊤
k+1yk
−d⊤
k gk
,
βFR
k+1 =
∥gk+1∥2
∥gk∥2
, βDY
k+1 =
∥gk+1∥2
d⊤
k yk
, βCD
k+1 =
∥gk+1∥2
−d⊤
k gk
.
Rn
3
[Narushima et al., 2011]
η0 := −g0 k ≥ 0
ηk+1 :=
⎧
⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
−gk+1 if g⊤
k+1pk+1 = 0,
−gk+1 + βk+1ηk − βk+1
g⊤
k+1ηk
g⊤
k+1pk+1
pk+1 otherwise.
pk ∈ Rn
( ) 2016 3 10 54 / 67

56. 1
2
3
4
5
( ) 2016 3 10 55 / 67

57. [Sato & Iwai, 2013]
A ∈ Rm×n
, m ≥ n
p ≤ n N = diag(µ1, . . . , µp), µ1 > · · · > µp > 0
4.1
minimize − tr(UT
AVN),
subject to (U, V) ∈ St(p, m) × St(p, n).
(U∗, V∗) U∗, V∗
A p
2
( ) 2016 3 10 56 / 67

58. [Yger et al., 2012]
0 2 X ∈ RT×m
, Y ∈ RT×n
CX = XT
X, CY = YT
Y, CXY = XT
Y
u ∈ Rm
, v ∈ Rn
f = Xu, g = Yv
2 f g ρ
ρ =
Cov(f, g)
Var(f) Var(g)
=
uT
CXYv
√
uTCXu
√
vTCYv
.
ρ
4.2
maximize uT
CXYv,
subject to uT
CXu = vT
CYv = 1.
2
( ) 2016 3 10 57 / 67

59. [Yger et al., 2012]
u, v
4.3
maximize tr(UT
CXYV),
subject to (U, V) ∈ StCX
(p, m) × StCY
(p, n).
n G
StG(p, n)
StG(p, n) = {Y ∈ Rn×p
| YT
GY = Ip}
2
( ) 2016 3 10 58 / 67

60. [Sato & Sato, 2015]
˙x =Ax + Bu,
y =Cx.
u ∈ Rp
y ∈ Rq
x ∈ Rn
˙xm =Amxm + Bmu,
ym =Cmxm.
Am = UT
AU, Bm = UT
B, Cm = CU, U ∈ Rn×m
U
UT
U = Im
( ) 2016 3 10 59 / 67

61. [Sato & Sato, 2015]
4.4
minimize J(U),
subject to U ∈ St(m, n).
J
J(U) := ∥Ge∥2 = tr(CeEcCT
e ) = tr(BT
e EoBe)
Ae =
A 0
0 UT
AU
, Be =
B
UT
B
, Ce = C −CU Ec
Eo
AeEc + EcAT
e + BeBT
e =0, AT
e Eo + EoAe + CT
e Ce = 0.
( ) 2016 3 10 60 / 67

62. [Kasai & Mishra, 2015]
X∗
∈ Rn1×n2×n3
: 3
Ω ⊂ {(i1, i2, i3) | id ∈ {1, 2, . . . , nd}, d ∈ {1, 2, 3}}
X∗
i1i2i3
(i1, i2, i3) ∈ Ω
PΩ(X)(i1,i2,i3) =
⎧
⎪⎪⎨
⎪⎪⎩
Xi1i2i3
if (i1, i2, i3) ∈ Ω
0 otherwise
r = (r1, r2, r3)
4.5
minimize
1
|Ω|
∥PΩ(X) − PΩ(X∗
)∥2
F,
subject to X ∈ Rn1×n2×n3
, rank(X) = r.
( ) 2016 3 10 61 / 67

63. [Kasai & Mishra, 2015]
X ∈ Rn1×n2×n3
r
X = G×1U1×2U2×3U3, G ∈ Rr1×r2×r3
, Ud ∈ St(rd, nd), d = 1, 2, 3.
→ M := St(r1, n1) × St(r2, n2) × St(r3, n3) × Rr1×r2×r3
Od ∈ O(rd), d = 1, 2, 3
(U1, U2, U3, G) → (U1O1, U2O2, U3O3, G ×1 OT
1 ×2 OT
2 ×3 OT
3 )
X
M/(O(r1) × O(r2) × O(r3))
( ) 2016 3 10 62 / 67

64. [Yao et al., 2016]
1
DSIEP (Doubly Stochastic Inverse Eigenvalue Problem):
self-conjugate {λ1, λ2, . . . , λn}
n × n C
λ1, λ2, . . . , λn
λi
( ) 2016 3 10 63 / 67

65. [Yao et al., 2016]
Oblique OB := {Z ∈ Rn×n
| diag(ZZT
) = In}
Λ := diag(λ1, λ2, . . . , λn)
U:
1 Z ⊙ Z, Z ∈ OB
(Z ⊙ Z)T
1n − 1n = 0
Z ⊙ Z λ1, λ2, . . . , λn
Z ⊙ Z = Q(Λ + U)QT
, Q ∈ O(n), U ∈ U
( ) 2016 3 10 64 / 67

66. [Yao et al., 2016]
H1(Z, Q, U) := Z ⊙ Z − Q(Λ + U)QT
, H2(Z) := (Z ⊙ Z)T
1n − 1n
H(Z, Q, U) := (H1(Z, Q, U), H2(Z))
4.6
minimize h(Z, Q, U) :=
1
2
∥H(Z, Q, U)∥2
F,
subject to (Z, Q, U) ∈ OB × O(n) × U.
OB × O(n) × U
( ) 2016 3 10 65 / 67

67. 1
2
3
4
5
( ) 2016 3 10 66 / 67

68. ( ) 2016 3 10 67 / 67

70. I
[1] Absil, P.A., Mahony, R., Sepulchre, R.: Optimization
Algorithms on Matrix Manifolds. Princeton University Press,
Princeton, NJ (2008)
[2] Dai, Y.H., Yuan, Y.: A nonlinear conjugate gradient method
with a strong global convergence property. SIAM Journal
on Optimization 10(1), 177–182 (1999)
[3] Edelman, A., Arias, T.A., Smith, S.T.: The geometry of
algorithms with orthogonality constraints. SIAM Journal on
Matrix Analysis and Applications 20(2), 303–353 (1998)
[4] Fletcher, R., Reeves, C.M.: Function minimization by
conjugate gradients. The Computer Journal 7(2), 149–154
(1964)
( ) 2016 3 10 68 / 67

71. II
[5] Kasai, H., Mishra, B.: Riemannian preconditioning for
tensor completion. arXiv preprint arXiv:1506.02159v1
(2015)
[6] Narushima, Y., Yabe, H., Ford, J.A.: A three-term conjugate
gradient method with sufficient descent property for
unconstrained optimization. SIAM Journal on optimization
21(1), 212–230 (2011)
[7] Ring, W., Wirth, B.: Optimization methods on Riemannian
manifolds and their application to shape space. SIAM
Journal on Optimization 22(2), 596–627 (2012)
[8] Sato, H.: A Dai–Yuan-type Riemannian conjugate gradient
method with the weak Wolfe conditions. Computational
Optimization and Applications (2015)
( ) 2016 3 10 69 / 67

72. III
[9] Sato, H., Iwai, T.: A Riemannian optimization approach to
the matrix singular value decomposition. SIAM Journal on
Optimization 23(1), 188–212 (2013)
[10] Sato, H., Iwai, T.: A new, globally convergent Riemannian
conjugate gradient method. Optimization 64(4), 1011–1031
(2015)
[11] Sato, H., Sato, K.: Riemannian trust-region methods for H2
optimal model reduction. In: Proceedings of the 54th IEEE
Conference on Decision and Control, pp. 4648–4655
(2015)
[12] Tan, M., Tsang, I.W., Wang, L., Vandereycken, B., Pan,
S.J.: Riemannian pursuit for big matrix recovery. In:
Proceedings of the 31st International Conference on
Machine Learning, pp. 1539–1547 (2014)
( ) 2016 3 10 70 / 67

73. IV
[13] Yao, T.T., Bai, Z.J., Zhao, Z., Ching, W.K.: A Riemannian
Fletcher–Reeves conjugate gradient method for doubly
stochastic inverse eigenvalue problems. SIAM Journal on
Matrix Analysis and Applications 37(1), 215–234 (2016)
[14] Yger, F., Berar, M., Gasso, G., Rakotomamonjy, A.:
Adaptive canonical correlation analysis based on matrix
manifolds. In: Proceedings of the 29th International
Conference on Machine Learning (ICML-12), pp.
1071–1078 (2012)
( ) 2016 3 10 71 / 67