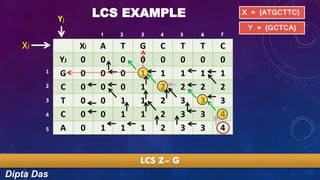
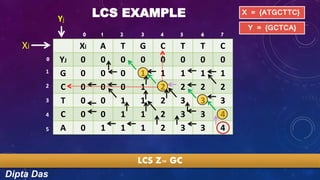
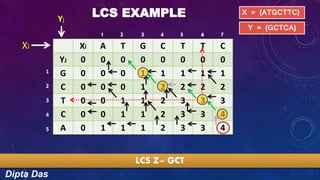
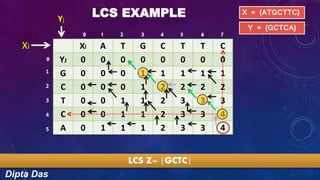
The document discusses the longest common subsequence (LCS) problem. It provides an example to calculate the LCS of two DNA sequences, X={ATGCTTC} and Y={GCTCA}, using a dynamic programming algorithm. The algorithm populates a 2D matrix by incrementing values when characters match and otherwise copying values from above or left. The LCS is read from the populated matrix as GCTC, demonstrating the method to find the longest common subsequence of two sequences.

1. Dipta Das
LONGEST COMMON
SUBSEQUENCE

2. Dipta Das
SUBSEQUENCE
A subsequence of given sequence is just the given sequence with zero or
more elements left out. Example..

3. Dipta Das
COMMON SUBSEQUENCE
Assume Two Sequence
Sequence Z is a common subsequence of X and Y if Z is a subsequence of both X and Y
Z={ B, C, A} length-3
Z={ B, C, A, B} length-4
Z={ B, C, B} length-3

4. Dipta Das
LONGEST COMMON SUBSEQUENCE
Theorem
Assume:
X=(X1, X2, X3…………………Xn)
Y=(Y1, Y2, Y3…………………Yn)
Any LCS of X and Y is Z, Z=(Z1, Z2,Z3……………..Zn)
IF Then
Xi = Yj Zk=Xi=Yj implies Zk-1 LCS of Xi-1 and Yj – 1
Xi ≠ Yj Zk ≠ Xi implies Zk-1 LCS of Xi-1 and Y
Xi ≠ Yj Zk ≠ Yj implies Zk-1 LCS of Yj-1 and X

5. Dipta Das
To Compare DNA of two (or more ) Different organisms

6. Dipta Das
EXAMPLE
Assume two DNA sequence
X = {ATGCTTC}
Y = {GCTCA}

7. Dipta Das
LCS EXAMPLE X = {ATGCTTC}
Y = {GCTCA}
A T G C T T C
G
C
T
C
A
1 2 3 4 5 6 7
1
2
3
4
5
Yj
Xi
0
0

8. Dipta Das
LCS EXAMPLE
A T G C T T C
0 0 0 0 0 0 0 0
G 0
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
1 2 3 4 5 6 7
1
2
3
4
5
Yj
Xi
0
0
Z[j,i]
Here I = 1, j = 1
Z[1,1]

9. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCAGA}
Yj
Xi
X Y
A G
Not Match
Maximum of
two box
z[J-1, i] and
[J, i-1]
1 2 3 4 5 6 7
1
2
3
4
5
0
0
Z[1,1]
Z[j-1, i]=Z[1-1, 1]= Z[0,1]
Z[j, i-1]=Z[1, 1-1]= Z[1,0]

10. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y
A G
Not Match
Lets Take from Upper one
Arrow indicate from
where you Take the
maximum.
1 2 3 4 5 6 7
1
2
3
4
5
0
0

11. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCAGA}
Yj
Xi
X Y Max
T G 0
Not Match
Lets Take from left one
Arrow indicate from
where you Take the
maximum.
arrow
1 2 3 4 5 6 7
1
2
3
4
5
0
0

12. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCAGA}
Yj
Xi
X Y Max
G G
Match
arrow
When match arrow will
be diagonal because we
will increment the
value of this cell
Z[i-1, j-1] + 10 = 1
1 2 3 4 5 6 7
1
2
3
4
5
0
0

13. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
G G
Match
arrow
Incremented value X[i-1] Y[j-1]
1 2 3 4 5 6 7
1
2
3
4
5
0
0
Z[I,j] = Z[3,1]

14. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {ACTCAGA}
Yj
Xi
X Y Max
C G 1
Not Match
Lets Take from left one
arrow
1 2 3 4 5 6 7
1
2
3
4
5
0
0

15. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
T G 1
Not Match
Lets Take from left one
arrow
0
0
1 2 3 4 5 6 7
1
2
3
4
5

16. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
T G 1
Not Match
Lets Take from left one
arrow
0
0
1 2 3 4 5 6 7
1
2
3
4
5

17. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
C G 1
Not Match
Lets Take from left one
arrow
1 2 3 4 5 6 7
1
2
3
4
5
0
0

18. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
A C 0
Not Match
Lets Take from left one
arrow
1 2 3 4 5 6 7
1
2
3
4
5
0
0

19. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
A C 0
Not Match
Lets Take from Upper one
arrow
0
0

20. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0 1
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
G C 1
Not Match
Lets Take from left one
arrow
1 2 3 4 5 6 7
1
2
3
4
5
0
0

21. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0 1 2
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
C C
Match
arrow
Increment Z[i-1,j-1]
1 2 3 4 5 6 7
1
2
3
4
5
0
0

22. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0 1 2 2
T 0
C 0
A 0
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
T C 2
Not Match
Lets Take from left one
arrow
1 2 3 4 5 6 7
1
2
3
4
5
0
0

23. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0 1 2 2 2 2
T 0 0 1 1 2 3 3 3
C 0 0 1 1 2 3 3 4
A 0 1 1 1 2 3 3 4
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
X Y Max
T G 1
Not Match
Lets Take from left one
arrow
In the same way…
1 2 3 4 5 6 7
1
2
3
4
5
0
0

24. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0 1 2 2 2 2
T 0 0 1 1 2 3 3 3
C 0 0 1 1 2 3 3 4
A 0 1 1 1 2 3 3 4
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
Firstly have to point out
highest value
For left and upper arrow
we will follow the
direction
For diagonal arrow we
will point out the
character for this cell.
1 2 3 4 5 6 7
1
2
3
4
5

25. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0 1 2 2 2 2
T 0 0 1 1 2 3 3 3
C 0 0 1 1 2 3 3 4
A 0 1 1 1 2 3 3 4
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
LCS Z= G
1 2 3 4 5 6 7
1
2
3
4
5

26. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0 1 2 2 2 2
T 0 0 1 1 2 3 3 3
C 0 0 1 1 2 3 3 4
A 0 1 1 1 2 3 3 4
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
LCS Z= GC
1 2 3 4 5 6 7
1
2
3
4
5
0
0

27. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0 1 2 2 2 2
T 0 0 1 1 2 3 3 3
C 0 0 1 1 2 3 3 4
A 0 1 1 1 2 3 3 4
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
LCS Z= GCT
1 2 3 4 5 6 7
1
2
3
4
5

28. Dipta Das
LCS EXAMPLE
Xi A T G C T T C
YJ 0 0 0 0 0 0 0 0
G 0 0 0 1 1 1 1 1
C 0 0 0 1 2 2 2 2
T 0 0 1 1 2 3 3 3
C 0 0 1 1 2 3 3 4
A 0 1 1 1 2 3 3 4
X = {ATGCTTC}
Y = {GCTCA}
Yj
Xi
LCS Z= {GCTC}
1 2 3 4 5 6 7
1
2
3
4
5
0
0

29. Dipta Das
ANY QUESTION?

30. Dipta Das
Thank You!