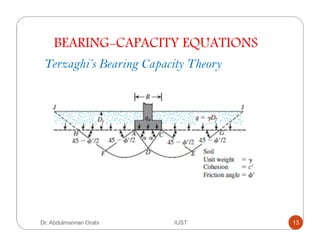
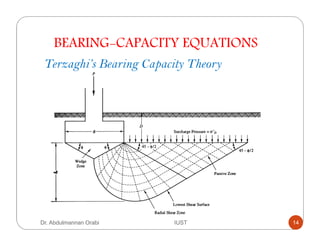
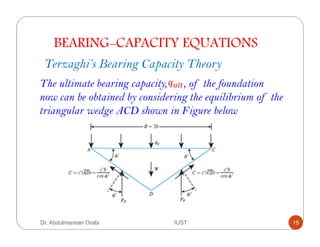
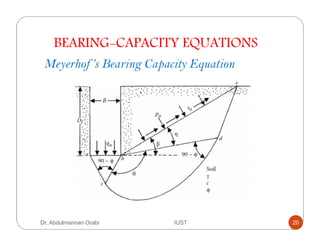
This lecture discusses the bearing capacity of foundations. It introduces Terzaghi's bearing capacity theory, which evaluates the ultimate bearing capacity of shallow foundations based on a failure surface geometry. Terzaghi's equation for ultimate bearing capacity is presented. Meyerhof's and Hansen's theories are also introduced, which improved on Terzaghi's theory. Hansen's theory provides a more general bearing capacity equation that can be applied to both shallow and deep foundations. Safety factors are applied to the ultimate bearing capacity to determine allowable bearing capacity for foundation design. Settlement criteria may also control and limit the allowable bearing capacity in some cases.

1. Lecture
2
INTERNATIONAL UNIVERSITY
FOR SCIENCE & TECHNOLOGY
‫وا‬ ‫م‬ ‫ا‬ ‫و‬ ‫ا‬ ‫ا‬
Dr. Abdulmannan Orabi
Civil Engineering and Environmental
Department
303421: Foundation Engineering
Bearing Capacity of Foundation

2. References
ACI 318M-14 Building Code Requirements for Structural
Concrete ( ACI 318M -14) and Commentary, American
Concrete Institute, ISBN 978-0-87031-283-0.
Bowles , J.,E.,(1996) “Foundation Analysis and Design” -5th
ed. McGraw-Hill, ISBN 0-07-912247-7.
Das, B., M. (2012), “ Principles of Foundation Engineering ”
Eighth Edition, CENGAGE Learning,
ISBN-13: 978-1-305-08155-0.
Syrian Arab Code for Construction 2012
Dr. Abdulmannan Orabi IUST 2

3. Bearing Capacity of Foundation
The soil must be capable of carrying the loads from
any engineered structure placed upon it without a
shear failure and with the resulting settlements
being tolerable for that structure.
This lecture will be concerned with evaluation of
the limiting shear resistance, or ultimate bearing
capacity of the soil under a foundation load.
3Dr. Abdulmannan Orabi IUST

4. It is necessary to investigate both base shear
resistance and settlements for any structure.
Bearing Capacity of Foundation
In many cases settlement criteria will control
the allowable bearing capacity; however, there
are also a number of cases where base shear (in
which a base punches into the ground - usually
with a simultaneous rotation) dictates the
recommended bearing capacity.
Dr. Abdulmannan Orabi IUST 4

5. Bearing Capacity of Foundation
Structures such as liquid storage tanks and mats are
often founded on soft soils, which are usually more
susceptible to base shear failure than to settlement.
Base shear control, to avoid a combination base
punching with rotation into the soil, is often of more
concern than settlement for these foundation types.
Dr. Abdulmannan Orabi IUST 5

6. Allowable Bearing Capacity
The recommendation for the allowable bearing
capacity to be used for design is based on the
minimum of either :
1. Limiting the settlement to a tolerable amount
2. The ultimate bearing capacity, which considers soil
strength, as computed in the following sections
Dr. Abdulmannan Orabi IUST 6

7. Allowable Bearing Capacity
The allowable bearing capacity based on shear
control is obtained by reducing (or dividing)
the ultimate bearing capacity (based on soil
strength) by a safety factor SF that is deemed
adequate to avoid a base shear failure to obtain
=
.
(2-1)
The safety factor is based on the type of soil (cohesive or cohesionless),
reliability of the soil parameters, structural information (importance,
use, etc.), and consultant caution.
Dr. Abdulmannan Orabi IUST 7

8. Dr. Abdulmannan Orabi IUST
Allowable Bearing Capacity
Most building codes provide an allowable
settlement limit for a foundation, which
may be well below the settlement derived
corresponding to given by equations( 2-1).
Thus, the bearing capacity corresponding to the
allowable settlement must also be taken into
consideration.
8

9. BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Theory
Terzaghi (1943) was the first to present a comprehensive
theory for the evaluation of the ultimate bearing capacity
of rough shallow foundations. According to this theory, a
foundation is shallow if its depth, Df (Figure slid 11), is
less than or equal to its width. Later investigators,
however, have suggested that foundations with Df equal
to 3 to 4 times their width may be defined as shallow
foundations.
Dr. Abdulmannan Orabi IUST 9

10. BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Theory
The effect of soil above the bottom of the foundation may also
be assumed to be replaced by an equivalent surcharge,
(where is the unit weight of soil).
= ∗
Terzaghi suggested that for a continuous, or strip, foundation
(i.e., one whose width-to-length ratio approaches zero), the
failure surface in soil at ultimate load may be assumed to be
similar to that shown in Figure on Slide 11.
Dr. Abdulmannan Orabi IUST 10

11. The failure zone under the foundation can be
separated into three parts (see Figure 4.6):
1. The triangular zone ACD immediately under
the foundation
2. The radial shear zones ADF and CDE, with the
curves DE and DF being arcs of a logarithmic
spiral
3. Two triangular Rankine passive zones AFH
and CEG
BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Theory
Dr. Abdulmannan Orabi IUST 11

12. BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Theory
The angles CAD and ACD are assumed to be equal to the
soil friction angle .
Note that, with the replacement of the soil above the bottom
of the foundation by an equivalent surcharge q, the shear
resistance of the soil along the failure surfaces GI and HJ
was neglected.
∅
Dr. Abdulmannan Orabi IUST 12

13. BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Theory
Dr. Abdulmannan Orabi IUST 13

14. BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Theory
Dr. Abdulmannan Orabi IUST 14

15. BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Theory
The ultimate bearing capacity, , of the foundation
now can be obtained by considering the equilibrium of the
triangular wedge ACD shown in Figure below
Dr. Abdulmannan Orabi IUST 15

16. BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Equation
= 0.5 + +
, , ! "# # "$ % & ' &$() * &(+",
and depends on angle of shearing resistance (ø)
( . /. 4 − 1 , ,)
4ℎ#"#:
= 4$!(ℎ +* (ℎ# *++($ %
= 7 $( 4#$%ℎ( +* (ℎ# ,+$8 /#8+4 (ℎ# *+7 ! ($+ 8#9#8
= ∗
= 0 , = 1 ! : = 1.5 ; + 1 = 5.71 *+" ∅ = 0
Dr. Abdulmannan Orabi IUST 16

17. BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Equation
= 0.5 + +
, , ! = ℎ ' * &(+",
Shape factors for the Terzaghi equations
Sγ Sq SC
Square 0.8 1 1.3
Circular 0.6 1 1.3
Rectangular 1-0.2 B/L 1 1+0.3 B/L
Dr. Abdulmannan Orabi IUST 17

18. BEARING-CAPACITY EQUATIONS
Terzaghi’s Bearing Capacity Theory
for Local Shear Failure
Terzaghi suggested the following relationships for
local shear failure in soil:
where
, , ! "# =+!$*$#! /# "$ % * &(+",
= 0.5 + +
=
2
3
tan ∅ = tan (
2
3
∅)
Dr. Abdulmannan Orabi IUST 18

19. BEARING-CAPACITY EQUATIONS
Meyerhof ’s Bearing Capacity Equation
In 1951, Meyerhof published a bearing capacity theory
that could be applied to rough, shallow, and deep
foundations. The failure surface at ultimate load under a
continuous shallow foundation assumed by Meyerhof is
shown in Figure below.
Dr. Abdulmannan Orabi IUST 19

20. BEARING-CAPACITY EQUATIONS
Meyerhof ’s Bearing Capacity Equation
Dr. Abdulmannan Orabi IUST 20

21. BEARING-CAPACITY EQUATIONS
Meyerhof ’s Bearing Capacity Equation
In this figure abc is the elastic triangular, bcd is the
radial shear zone with cd being an arc of a log spiral,
and bde is a mixed shear zone in which the shear varies
between the limits of radial and plane shears depending
on the depth and roughness of the foundation.
The plane be is called an equivalent free surface.
Dr. Abdulmannan Orabi IUST 21

22. BEARING-CAPACITY EQUATIONS
Meyerhof ’s Bearing Capacity Equation
Vertical load:
= 0.5 ! + ! + !
= 0.5 $ ! + $ ! + $ !
Inclined load:
Dr. Abdulmannan Orabi IUST 22

23. BEARING-CAPACITY EQUATIONS
Meyerhof ’s Bearing Capacity Equation
tan 2
( ) tan (45 )
2
qN eπ φ φ
= +
( 1)cotC qN N φ= −
( 1) tan(1.4 )qN Nγ φ= −
where
, , ! "# # "$ % & ' &$() * &(+",
= 0 , = 1 ! : = ; + 2 = 5.14 *+" ∅ = 0
Dr. Abdulmannan Orabi IUST 23

24. BEARING-CAPACITY EQUATIONS
Meyerhof ’s Bearing Capacity Equation
where
, , ! = ℎ '# * &(+",
1 0.1 .......... 10q p
B
S S K for
L
γ φ= = + × ≥
1 0.2c p
B
S K
L
= + ×
CD = ( E
(45 +
∅
2
)
= = 1 *+" ∅ = 0
24Dr. Abdulmannan Orabi IUST

25. ! , ! , ! ! = #'(ℎ * &(+",
BEARING-CAPACITY EQUATIONS
Meyerhof ’s Bearing Capacity Equation
where
1 0 .2 f
C p
D
d K
B
= + ×
1 0.1 .... 10f
q p
D
d d K for
B
γ φ= = + × ≥
! = ! = 1 *+" ∅ = 0
Dr. Abdulmannan Orabi IUST 25

26. $ , $ , ! $ = F &8$ ($+ * &(+",
BEARING-CAPACITY EQUATIONS
Meyerhof ’s Bearing Capacity Equation
where
$ = $ = 1 −
G
90
E
) ∅
$ = 1 −
G
∅
E
∅ > 0
$ = 0 *+" G ≠ 0 ! ∅ = 0
G<∅
V
H
R
Dr. Abdulmannan Orabi IUST 26

27. BEARING-CAPACITY EQUATIONS
Hansen’s Bearing Capacity Equation ( General Equation )
Df
V
η
+β
Dr. Abdulmannan Orabi IUST 27

28. BEARING-CAPACITY EQUATIONS
Hansen’s Bearing Capacity Equation ( General Equation )
'
0.5ult q q q q q q C C C C C Cq B N S d i g b qN S d i g b CN S d i g bγ γ γ γ γ γγ= + +
tan 2
( ) tan (45 )
2
qN eπ φ φ
= +
( 1)cotC qN N φ= −
( 1) tan(1.4 )qN Nγ φ= −
where
, , ! "# # "$ % & ' &$() * &(+",
= 0 , = 1 ! : = ; + 2 = 5.14 *+" ∅ = 0
Dr. Abdulmannan Orabi IUST 28

29. BEARING-CAPACITY EQUATIONS
Hansen’s Bearing Capacity Equation ( General Equation )
'
0.5ult q q q q q q C C C C C Cq B N S d i g b qN S d i g b CN S d i g bγ γ γ γ γ γγ= + +
where
, , ! = ℎ '# * &(+",
'
'
1
q
C
C
N B
S
N L
= + ×
'
'
1 sinq
B
S
L
φ= +
'
'
1 0.4
B
S
L
γ = − ≥ 0.6
Dr. Abdulmannan Orabi IUST 29

30. ! , ! , ! ! = #'(ℎ * &(+",
where
BEARING-CAPACITY EQUATIONS
Hansen’s Bearing Capacity Equation ( General Equation )
'
0.5ult q q q q q q C C C C C Cq B N S d i g b qN S d i g b CN S d i g bγ γ γ γ γ γγ= + +
1 0 .4Cd K= +
2
1 2 ta n (1 s in )qd Kφ φ= + −
1
1
tan ( ) 1
f f
f f
D D
K for
B B
D D
K for
B B
−
= ≤
= f
! = 1 *+" 88 ∅
30

31. BEARING-CAPACITY EQUATIONS
Hansen’s Bearing Capacity Equation ( General Equation )
'
0.5ult q q q q q q C C C C C Cq B N S d i g b qN S d i g b CN S d i g bγ γ γ γ γ γγ= + +
$ , $ , ! $ = F &8$ ($+ * &(+",
where
1
1
q
C q
q
i
i i
N
−
= −
−
1
0.5
(1 )
cot
i
q
f a
H
i
V A C
α
φ
= −
+
2
0.7
(1 )
cot
i
f a
H
i
V A C
α
γ
φ
= −
+
2
(0.7 / 450)
(1 )
cot
o
i
f a
H
i
V A C
α
γ
η
φ
−
= −
+
2 ≤ OP ! OE ≤ 5
Dr. Abdulmannan Orabi IUST 31

32. BEARING-CAPACITY EQUATIONS
Hansen’s Bearing Capacity Equation ( General Equation )
'
0.5ult q q q q q q C C C C C Cq B N S d i g b qN S d i g b CN S d i g bγ γ γ γ γ γγ= + +
where
% , % , ! % = Q"+7 ! * &(+",
% =
RS
147S
% = 1 −
RS
147S
% = % = 1 − 0.5 ( R T
Dr. Abdulmannan Orabi IUST 32

33. BEARING-CAPACITY EQUATIONS
Hansen’s Bearing Capacity Equation ( General Equation )
'
0.5ult q q q q q q C C C C C Cq B N S d i g b qN S d i g b CN S d i g bγ γ γ γ γ γγ= + +
where
/ , / , ! / = ,# * &(+",
/ =
US
147S
*+" ∅ = 0
/ = 1 −
US
147S
/ = exp (−2U ( ∅) / = exp (−2.7 U ( ∅)
U $ " !$ ,
Dr. Abdulmannan Orabi IUST 33

34. BEARING-CAPACITY EQUATIONS
Hansen’s Bearing Capacity Equation ( General Equation )
= 5.14 1 + + ! − $ − % − / + *+" ∅ = 0
Where :
= 0.2
Y
! = 0.4 Z
$ = 0.5 − 1 −
[
]
/ =
US
147S
*+" ∅ = 0
% =
RS
147S
Dr. Abdulmannan Orabi IUST 34

35. The equation for ultimate bearing capacity by Terzaghi
has been developed based on assumption that water table
is located at a great depth .
If the water table is located close to foundation ; the
equation needs modification.
The effective unit weight of the soil is used in the
bearing-capacity equations for computing the ultimate
capacity.
BEARING-CAPACITY EQUATIONS
Effect of Water Table on Bearing Capacity
Dr. Abdulmannan Orabi IUST 35

36. BEARING-CAPACITY EQUATIONS
Effect of Water Table on Bearing Capacity
The water table is seldom above the base of the footing,
as this would, at the very least, cause construction
problems. If it is, however, the q term requires
adjusting so that the surcharge pressure is an effective
value and an effective unit weight must be used in the
0.5 ϒB Nϒ term.
Water table above the base of footing
Water table below the base of footing
!^
G.W.T.
G.W.T.
Dr. Abdulmannan Orabi IUST 36

37. BEARING-CAPACITY EQUATIONS
Effect of Water Table on Bearing Capacity
= 2 [ − !^
!^
[E
+
[E
[ − !^
E
4ℎ#"# [ = 0.5 tan ( 45 + ∅/2)
!^ = !#'(ℎ +* 4 (#" ( /8# /#8+4 / ,# +* *++($ %
= 7 $( 4#$%ℎ( +* ,+$8 $ !#'(ℎ !^
= ,7/=#"%#! 7 $( 4#$%ℎ( /#8+4 4 (#" ( /8#
When the water table lies within the wedge zone,
can compute the average effective weight of the
soil in the wedge zone as
Dr. Abdulmannan Orabi IUST 37

38. When the water table is below the wedge zone [depth
approximately ], the water table effects
can be ignored for computing the bearing capacity.
BEARING-CAPACITY EQUATIONS
Effect of Water Table on Bearing Capacity
[ = 0.5 tan ( 45 + ∅/2)
Water table below the
base of the footing
!^ > [
G.W.T.
Dr. Abdulmannan Orabi IUST 38

39. BEARING-CAPACITY EQUATIONS
Effect of Soil Compressibility
The change of failure mode is due to soil compressibility, to
account for which Vesic (1973) proposed the following
modification of bearing capacity equation :
= 0.5 ! + ! + !
, ! "# ,+$8 &+='"#,,$/$8$() * &(+",
Where :
Dr. Abdulmannan Orabi IUST 39

40. BEARING-CAPACITY EQUATIONS
Effect of Soil Compressibility
The soil compressibility factors were derived by Vesic
(1973) by analogy to the expansion of cavities.
According to that theory, in order to calculate
,the following steps should be taken:
, !
Step 1. Calculate the rigidity index, Ir, of the soil at a
depth approximately B/2 below the bottom of the
foundation, or
F` =
Qa
+ ( ∅4ℎ#"#
Qa = ,ℎ# " =+!787, +* ,+$8
= #**#&($9# +9#"/7"!# '"#,,7"# ( !#'(ℎ ( +
b
E
)
Dr. Abdulmannan Orabi IUST 40

41. BEARING-CAPACITY EQUATIONS
Effect of Soil Compressibility
Step 2. The critical rigidity index, , can be expressed asF`( `)
F`( `) =
1
2
#c' 3.3 − 0.45
Y
&+( 45 −
∅
2
Step 3. If , then F` ≥ F`( `) = = = 1
However, if , then F` < F`( `)
= = #c' −4.4 + 0.6
Y
( ∅ +
3.07,$ ∅ 8+%2F`
1 + ,$ ∅
: = 0.32 + 0.12
Y
+ 0.6 8+%F` *+" ∅ = 0
: = −
1 −
( ∅
*+" ∅ > 0
Dr. Abdulmannan Orabi IUST 41

42. BEARING-CAPACITY from SPT
Bearing Capacity from SPT
The SPT is widely used to obtain the bearing capacity of
soils directly.
Considering the accumulation of field observations and the
stated opinions of the authors and others, this author adjusted
the Meyerhof equations for an approximate 50 percent
increase in allowable bearing capacity to obtain the following:
2
55 0.3
(1 0.33 )
0.08
f
a
N DB
q
B B
+ 
= + 
 
> 1.2 = ≤ 1.2 =d + e. ff
gh
i
≤ d. ff
Dr. Abdulmannan Orabi IUST 42

43. BEARING-CAPACITY of Mat Foundation
The gross ultimate bearing capacity of a mat
foundation can be determined by the same equation used
for shallow foundations, or
= 0.5 $ ! + $ ! + $ !
The term B in Eq. above is the smallest dimension of the mat.
The net ultimate capacity of a mat foundation is
(jk ) = −
Dr. Abdulmannan Orabi IUST 43

44. BEARING-CAPACITY of Mat Foundation
The net allowable soil bearing capacity
(jk ) =
(jk )
. l
For mats on clay, the factor of safety should not be less
than 3 under dead load or maximum live load.
Under most working conditions, the factor of safety
against bearing capacity failure of mats on sand is
very large.
Dr. Abdulmannan Orabi IUST 44

45. Dr. Abdulmannan Orabi IUST
BEARING-CAPACITY of Mat Foundation
Bearing Capacity from SPT
The net allowable bearing capacity for mats constructed over
granular soil deposits can be adequately determined from the
standard penetration resistance numbers
(jk ) =
TT
0.08
ln
k(==)
25
(jk ) = 16.63 TT
k(==)
25
45