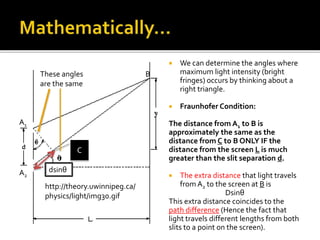
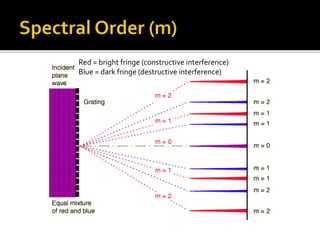
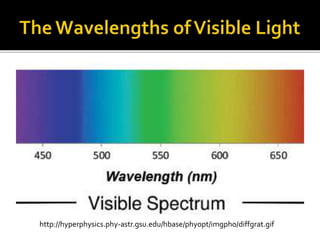
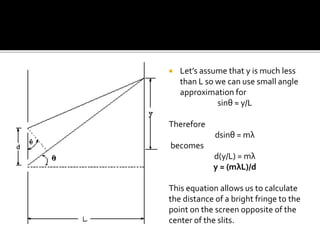
The document explains the principles of constructive and destructive interference in the context of light waves, highlighting the formation of bright and dark fringes on a screen. It outlines the conditions under which maximum light intensity occurs and provides equations to calculate fringe positions based on path differences. Additionally, it discusses the impact of different wavelengths on the spacing of bright fringes.

1. LearningObject – CamilleAlvarez (LC2)

2. PhET Simulation
• The points of
constructive
interference appear
as bright bands
(green) on the
screen.
• The points of
destructive
interference appear
as dark bands.
These bands are
referred to as “fringes”.
Let’s go into more
detail.

3.  We can determine the angles where
maximum light intensity (bright
fringes) occurs by thinking about a
right triangle.
 Fraunhofer Condition:
The distance from A1 to B is
approximately the same as the
distance from C to B ONLY IF the
distance from the screen L is much
greater than the slit separation d.
 The extra distance that light travels
from A2 to the screen at B is
Dsinθ
This extra distance coincides to the
path difference (Hence the fact that
light travels different lengths from both
slits to a point on the screen).
http://theory.uwinnipeg.ca/
physics/light/img30.gif
C
A1
A2
BThese angles
are the same
dsinθ

4. Assuming the light waves from the source are
in phase, the path difference for
 Constructive Interference:
Δx = mλ
 Destructive Interference:
Δx = (m+1/2)λ

5. Red = bright fringe (constructive interference)
Blue = dark fringe (destructive interference)

6.  When the path difference corresponds to
exactly a whole number of λ, constructive
interference (bright fringes) occurs.
 So:
Dsinθ = mλ
 For all values of m other than zero that is an
integer, the maxima for different
wavelengths have different angles.
 An m value of zero means that θ = 0 ° and the light would appear in the middle
of the screen.
Path difference Δx !!

7.  Accordingly, when the path difference
corresponds to an odd number of half λ,
destructive interference (the dark fringes)
occurs.
 So:
Dsinθ = (m+1/2)λ

8. http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/imgpho/diffgrat.gif

9.  Let’s assume that y is much less
than L so we can use small angle
approximation for
sinθ ≈ y/L
Therefore
dsinθ = mλ
becomes
d(y/L) = mλ
y = (mλL)/d
This equation allows us to calculate
the distance of a bright fringe to the
point on the screen opposite of the
center of the slits.

10. Red has the largest wavelength in
the visible spectrum.
Using
y = (mλ)L/d
we can see mathematically that the
distance between bright fringes is a
lot bigger than purple (smallest
wavelength).