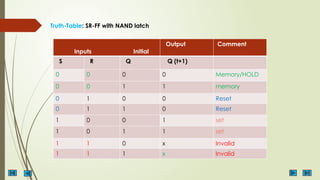
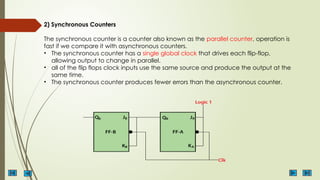
The document provides an overview of sequential circuits, highlighting their dependency on present inputs and previous states, unlike combinational circuits. It categorizes sequential circuits into asynchronous and synchronous types, detailing their characteristics, components like flip-flops and latches, and various triggering methods. Additionally, it describes different types of flip-flops such as SR, JK, D, and T flip-flops, along with their functions and truth tables.

1. SEQUENTIAL CIRCUIT
Unit-IV Digital Logic Circuits
CSE- Semester-III

2. Introduction:
The sequential circuit is a special type of circuit that has a series of inputs and outputs.
The outputs of the sequential circuits depend on both the combination of present inputs
and previous outputs. The previous output is treated as the present state.
The sequential circuit contains the combinational circuit and its memory storage elements.

3. Differences between Combinational and Sequential
circuits
1. The outputs of the combinational circuit
depend only on the present inputs.
2. The feedback path is not present in the
combinational circuit.
3. In combinational circuits, memory elements
are not required.
4. The clock signal is not required for
combinational circuits.
5. The combinational circuit is simple to design.
6. Elementary building blocks are only logic
gates.
7. These are faster logic circuits.
1. The outputs of the sequential circuits
depend on both present inputs and present
state(previous output).
2. The feedback path is present in the
sequential circuits.
3. In the sequential circuit, memory elements
play an important role and require.
4. The clock signal is required for sequential
circuits.
5. It is not simple to design a sequential circuit.
6. Elementary building blocks are Flip-Flops.
7. These circuits are slower than combinational
circuits.

4. Types of Sequential Circuits
1. Asynchronous sequential circuits
2. Synchronous sequential circuits
The asynchronous circuits do not use clock pulses. The asynchronous circuit is
operated through the pulses. The internal state is changed when the input variable
is changed. The un-clocked flip-flops or time-delayed are the memory elements of
asynchronous sequential circuits. The asynchronous sequential circuit is similar to the
combinational circuits with feedback.
In synchronous sequential circuits, synchronization of the memory element's state is
done by the clock signal. The output is stored in either flip-flops or latches(memory
devices). The synchronization of the outputs is done with either only negative edges
of the clock signal or only positive edges.

5. Clock Signal and Triggering
The clock signal refers to a periodic signal. A clock signal is considered as the square
wave. Sometimes, the signal stays at logic, either high 5V or low 0V, to an equal amount
of time.
Types of Triggering:
1. Level triggering
2. Edge triggering

6. Edge triggering:
1. Positive edge triggering: The transition from Logic Low to Logic High occurs in
the clock signal of positive edge triggering(rising edge).
2. Negative edge triggering: The transition from Logic High to Logic low occurs in
the clock signal of negative edge triggering(falling edge). So, in negative edge
triggering, the circuit is operated with such type of clock signal.

7. Level triggering : In level triggering, when the clock pulse is at a particular level, only
then the circuit is activated.
1. Positive level triggering: In a positive level triggering, the signal with Logic High
occurs. So, in this triggering, the circuit is operated with such type of clock signal.
2. Negative level triggering: In negative level triggering, the signal with Logic Low
occurs. So, in this triggering, the circuit is operated with such type of clock signal. Below
is the diagram of Negative level triggering:
Clock Signal and Triggering

8. Flip-Flop
A flip-flop is a binary storage device capable of storing one bit of information. In
a stable state, the output of a flip-flop is either 0 or 1.
Latches are the building blocks of Flip-Flops.
• Latch is an electronic logic circuit with two stable states i.e. it is a bistable
multivibrator. Latch has a feedback path to retain the information. One can use it
to store either 0 or 1 at a specified time.
• They are used in digital systems as temporary storage elements to store binary
information.
• Latches can be implemented using various digital logic gates, such as AND, OR,
NOT, NAND, and NOR gates.
• Latches controlled by a clock transition of flip-flops.
Latch

9. The types of latches are classified as:
Latch:
• SR Latch
• Gated S-R Latch
• D latch
• Gated D Latch
• JK Latch
• T Latch.
SR Latch: The SR latch is a circuit with two cross-coupled NOR gates or two cross-
coupled NAND gates, and two inputs labeled S for set and R for reset.
• The output of SR depends on current as well as previous state. And its state changes
as soon as input change.

10. Latch:
Graphical symbol:

11. SR Latch : Logic Diagram

12. Latch:
• SR Latch with NOR gate
Case-1: S = 0 , R = 1 , Q = 0 and Q’ = 1
S= 0 , R = 0, Q = 0 and Q’ = 1 (Memory state or HOLD state)
Case-II : S = 1, R = 0, Q =1 and Q’ = 0
S = 0, R = 0, Q = 1 and Q’ = 0 (Memory state or HOLD state)
Case –III : S=1 ,R = 1, Q = 0 and Q’ = 0 (Forbidden or Invalid state)

13. Latch:
• SR Latch with NOR gate
Case-1: S = 0 , R = 1 , Q = 0 and Q’ = 1
S= 0 , R = 0, Q = 0 and Q’ = 1 (Memory state or HOLD state)
Case-II : S = 1, R = 0, Q =1 and Q’ = 0
S = 0, R = 0, Q = 1 and Q’ = 0 (Memory state or HOLD state)
Case –III : S=1 ,R = 1, Q = 0 and Q’ = 0 (Forbidden or Invalid state)
HOLD

14. Latch:
• SR Latch with NOR gate
Case-1: S = 0 , R = 1 , Q = 0 and Q’ = 1
S= 0 , R = 0, Q = 0 and Q’ = 1 (Memory state or HOLD state)
Case-II : S = 1, R = 0, Q =1 and Q’ = 0
S = 0, R = 0, Q = 1 and Q’ = 0 (Memory state or HOLD state)
Case –III : S=1 ,R = 1, Q = 0 and Q’ = 0 (Forbidden or Invalid state)
S R Q Q’
0 0 Memory/HOLD
0 1 0 1
1 0 1 0
1 1 Invalid

15. Latch:
• Assignment-2
Q1. Discuss SR Latch with AND gate in detail :

16. D- Latch(Transparent latch)
This indeterminate condition makes this circuit difficult to manage, and it is seldom
used in practice. Nevertheless, the SR latch is an important circuit because other
useful latches and flip-flops are constructed from it.

17. D- Latch(Transparent latch)
This indeterminate condition makes this circuit difficult to manage, and it is seldom
used in practice. Nevertheless, the SR latch is an important circuit because other
useful latches and flip-flops are constructed from it.
Graphical symbol:

18. D- Latch(Transparent latch)
Logic Circuit:
This latch has only two inputs: D (data) and En (enable). The D input goes directly to the
S input, and its complement is applied to the R input.
• when En = 1. If D = 1, the Q = 1, placing the circuit in the set state.
• If D = 0, output Q = 0, placing the circuit in the reset state.

19. Flip-Flop:
A flip-flop is a binary storage device capable of storing one bit of information. In
a stable state, the output of a flip-flop is either 0 or 1.
• Its output remains in either of the stable states(0/1) until an external event
(known as a trigger) is applied.
• The state of a latch or flip-flop is switched by a change in the control input.
• Latches are said to be level sensitive devices; flip-flops are edge-sensitive
devices.
• The key to the proper operation of a flip-flop is to trigger it only during a
signal transition .
Types:
• SR Flip-flop
• JK Flip-flop
• D-flip-flop
• T-flip-flop

20. Graphical Symbol:

21. SR-Flip-Flop:
The SR flip-flop is the simplest type of flip-flop. SR stands for “set” and “reset”. It has two
inputs, ‘S’ and ‘R’, and two outputs, Q and Q’. As with latches.
• based on the logic gates used, we can have two types of SR Flip-Flops: NOR and
NAND flip-flops.
SR- FF with NAND latch
NAND SR-Latch
R*
S*

22. SR-Flip-Flop:
SR- FF with NAND latch
NAND SR-Latch
R*
S*
S* R* Q Q’
0 0 Invalid
0 1 1 0
1 0 0 1
1 1 Memory

23. SR-Flip-Flop NAND latch:
NAND SR-Latch
R*
S*
S* = S’ + clk’ R* = R’ + clk’
If clk = 0 S* = 1 , R* = 1 (i.e. Memory state)

24. SR- Flip-Flop
If clk =1, S* = S’ and R* = R’
• If S =0 , R= 0 S* = 1 , R* = 1 (memory state)
• S =0 , R= 1 S* = 1 , R* = 0 (Reset state)
• S =1 , R= 0 S* = 0 , R* = 1 (set state)
• S =1 , R= 1 S* = 0 , R* = 0 (Invalid state)
SR-Latch

25. Inputs Initial
Output Comment
S R Q Q (t+1)
0 0 0 0 Memory/HOLD
0 0 1 1 memory
0 1 0 0 Reset
0 1 1 0 Reset
1 0 0 1 set
1 0 1 1 set
1 1 0 x Invalid
1 1 1 x Invalid
Truth-Table: SR-FF with NAND latch

26. Initial
Inputs
Output Comment
Q S R Q (t+1)
0 0 0 0 Memory/HOLD
0 0 1 0 Reset
0 1 0 1 set
0 1 1 x Indeterminate
1 0 0 1 Memory/HOLD
1 0 1 0 Reset
1 1 0 1 set
1 1 1 x Indeterminate
Truth-Table: SR-FF with NAND latch
0 0 x 1
1 0 x 1
Q
SR
Q(t+1) = S + Q.R’
Characteristics equation:

27. Function-table SR-FF with NAND latch
CLK S R Q
0 x X Memory
1 0 0 Memory
1 0 1 Reset
1 1 0 Set
1 1 1 Indeterminate
Excitation Table:
Q Q(t+1) S R
0 0 0 x
0 1 1 0
1 0 0 1
1 1 x 0
Excitation table: this table depends upon the truth table and describes what should be the behavior
of the circuit for the desired output.

28. SR-FF using NOR latch:
Q
Q’

29. Initial Inputs Output Comment
Q(present) S R Q (t+1)(next)
0 0 0 0 Memory/HOLD
0 0 1 0 Reset
0 1 0 1 set
0 1 1 x Indeterminate
1 0 0 1 Memory/HOLD
1 0 1 0 Reset
1 1 0 1 set
1 1 1 x Indeterminate
Truth-Table: SR-FF with NOR latch

30. Initial
Inputs
Output Comment
Q S R Q (t+1)
0 0 0 0 Memory/HOLD
0 0 1 0 Reset
0 1 0 1 set
0 1 1 x Indeterminate
1 0 0 1 Memory/HOLD
1 0 1 0 Reset
1 1 0 1 set
1 1 1 x Indeterminate
Truth-Table: SR-FF with NOR gate
0 0 x 1
1 0 x 1
Q
SR
Q(t+1) = S + Q.R’

31. Function-table SR-FF with NOR gate
CLK S R Q
1 0 0 Memory
1 0 1 Reset
1 1 0 Set
1 1 1 Indeterminate
Excitation Table:
Q Q(t+1) S R
0 0 0 x
0 1 1 0
1 0 0 1
1 1 x 0

32. JK-FF
To avoid undesired undefined state(S = 1, R = 1) in SR flip-flops, it’s imperative to
design the circuit such that both inputs are never set to 1 at the same time.
• The JK Flip flop can be viewed as a modification of the SR Flip flop.
• The JK Flip-flop is also called a programmable flip-flop or considered to be a
universal flip-flop circuit, because it can be used to realize the action of any of
the other flip-flop types.
Applications:
• They are essential component for Counter, Frequency divider.
• These are used to design shift register.
• These are also used in designing of Memory units(.e.g. RAM).

33. JK-Flip-Flop
Boolean Expression..??

34. JK-Flip-Flop using NAND gate
1
1 1 1
J
KQ
Q(n+1) = J.Q’ + K’. Q

35. Function Table: JK-flip-Flop
Clk J K Q(n+1)
0 X X Qn (HOLD)
1 0 0 Qn (HOLD)
1 0 1 0
1 1 0 1
1 1 1 Qn’(Toggle)

36. Function Table: JK-flip-Flop
Clk J K Q(n+1)
0 X X Qn (HOLD)
1 0 0 Qn (HOLD)
1 0 1 0
1 1 0 1
1 1 1 Qn’(Toggle)
Qn Q(n+1) J K
0 0 0 X
0 1 1 X
1 0 x 1
1 1 x 0
Excitation table:

37. Toggle state: J = 1, K = 1, Clk = 1, Q =0 Q’ =1
1
1
1
0
1
0
1
1
1
0
0
1
n n+1

38. Toggle state: J = 1, K = 1, Clk = 1,
1
1
1
0
1
0
1
1
1
0
0
1
n n+1
SR latch using NAND
S = 0 , R = 1 Q = 1, Q’ = 0 Flip-flop

39. D-Flip Flop
D flip-flop is also called data flip-flop or delay flip-flop. Its construction is also
similar to the SR flip-flop except the inputs are connected by NOT Gate. If we
see from the outside we will see it has one CLK and one input but actually it has
two input.

40. D-Flip Flop
D flip-flop is also called data flip-flop or delay flip-flop. Its construction is also
similar to the SR flip-flop except the inputs are connected by NOT Gate. If we
see from the outside we will see it has one CLK and one input but actually it has
two input.
Truth Table:
Q D Q(t+1)
0 0 0
0 1 1
1 0 0
1 1 1

41. D-Flip Flop
D flip-flop is also called data flip-flop or delay flip-flop. Its construction is also
similar to the SR flip-flop except the inputs are connected by NOT Gate. If we
see from the outside we will see it has one CLK and one input but actually it has
two input.
Truth Table:
Characteristics Equation: Q(t+1) = D
Q D Q(t+1)
0 0 0
0 1 1
1 0 0
1 1 1

42. D-Flip Flop:
CLK D Q(t+1)
0 X Q(t)
1 0 0
1 1 1
Q(t) Q(t+1) D
0 0 0
0 1 1
1 0 0
1 1 1
Function Table:
Excitation Table:

43. T-Flip Flop:
T flip-flop is also called toggle flip-flop. the construction of the T flip-flop is same as the
JK flip-flop except both input terminal is connected together and taken out one
terminal which is known as T terminal or toggle terminal. It also actually two input
and one CLK but as the two input terminal is connected together it has one input
and one CLK terminal outside.

44. T-Flip Flop:
T flip-flop is also called toggle flip-flop. the construction of the T flip-flop is same as the
JK flip-flop except both input terminal is connected together and taken out one
terminal which is known as T terminal or toggle terminal. It also actually two input
and one CLK but as the two input terminal is connected together it has one input
and one CLK terminal outside.
T Q(t) Q(t+1) Comment
0 0 0 No change
0
1 1 No change
1 0 1 Toggle
1 1 0 Toggle
Truth-Table:

45. T-Flip Flop:
T flip-flop is also called toggle flip-flop. the construction of the T flip-flop is same as the
JK flip-flop except both input terminal is connected together and taken out one
terminal which is known as T terminal or toggle terminal. It also actually two input
and one CLK but as the two input terminal is connected together it has one input
and one CLK terminal outside.
T Q(t) Q(t+1)
0 0 0
0 1 1
1 0 1
1 1 0
Truth-Table:
Characteristics equation:
Q(t+1) = T’Q(t) + T.Q(t)’ = T xor Q(t)

46. T-Flip-Flop
Function table:
Excitation table:
Q(t) T Q(t+1) Comment
0 0 0 No change
0 1 1 Toggle
1 0 1 No change
1 1 0 Toggle
Q(t) Q(t+1) T
0 0 0
0 1 1
1 0 1
1 1 0

47. Register:
A register is basically a an array or a group of flip-flops used for storing binary
information. As we know that the flip-flop is the basic block of storage, one flip-flop
can store one bit of information.
• For storing n-bit in register, it will require 'n' number of flip-flops. Registers are mainly
used for storing and shifting information.
Application:
• Microprocessor, Serial adder, Counters, shift registers. Etc.

48. Register:
A register is basically a an array or a group of flip-flops used for storing binary
information. As we know that the flip-flop is the basic block of storage, one flip-flop
can store one bit of information.
• For storing n-bit in register, it will require 'n' number of flip-flops. Registers are mainly
used for storing and shifting information.
Application:
• Microprocessor, Serial adder, Counters, shift registers. Etc.
Shift register:
A register capable of shifting(Left or right) the binary information held in each cell
to its neighboring cell, in a selected direction, is called a shift register.

49. Types of shift registers:
• Serial IN serial OUT(SISO)
• Serial IN Parallel OUT(SIPO)
• Parallel IN serial OUT(PISO)
• Parallel IN Parallel OUT(PIPO)

50. Types of shift registers:
• Serial IN serial OUT(SISO)
• Serial IN Parallel OUT(SIPO)
• Parallel IN serial OUT(PISO)
• Parallel IN Parallel OUT(PIPO)

51. Types of shift registers:
• Serial IN serial OUT(SISO)
• Serial IN Parallel OUT(SIPO)
• Parallel IN serial OUT(PISO)
• Parallel IN Parallel OUT(PIPO)

52. Types of shift registers:
• Serial IN serial OUT(SISO)
• Serial IN Parallel OUT(SIPO)
• Parallel IN serial OUT(PISO)
• Parallel IN Parallel OUT(PIPO)

53. Types of shift registers:
• Serial IN serial OUT(SISO)
• Serial IN Parallel OUT(SIPO)
• Parallel IN serial OUT(PISO)
• Parallel IN Parallel OUT(PIPO)

54. Types of shift registers:
• Serial IN serial OUT(SISO)
• Serial IN Parallel OUT(SIPO)
• Parallel IN serial OUT(PISO)
• Parallel IN Parallel OUT(PIPO)
CLK QA QB QC QD(output)
0 0 0 0 0
1 1 1 0 1
1 0 1 1 0
1 0 0 1 1
1 0 0 0 1
Note: One CLK pulse is enough to load the 4-bit of data but four pulses are
required to unload all the four bits.

55. Types of shift registers:
• Serial IN serial OUT(SISO)
• Serial IN Parallel OUT(SIPO)
• Parallel IN serial OUT(PISO)
• Parallel IN Parallel OUT(PIPO)

56. Types of shift registers:
• Serial IN serial OUT(SISO)
• Serial IN Parallel OUT(SIPO)
• Parallel IN serial OUT(PISO)
• Parallel IN Parallel OUT(PIPO)
CLK QA QB QC QD(output)
0 0 0 0 0
1 1 1 0 1
The parallel data is loaded simultaneously into the register, and transferred
together to their respective outputs by the same clock pulse.

57. Shift Registers: summary
ModeOperation Uploading Reading total
SISO n n-1 2n-1
SIPO n 0 n
PISO 1 n-1 n
PIPO 1 0 1
Clock needed for n-bit Shift Register:

58. Counters
A special type of sequential circuit used to count the pulse is known as a counter, or a
collection of flip flops where the clock signal is applied is known as counters.
• counters are a special type of register.
• They exhibits a predetermined sequence of binary states.
These counters find utility in diverse digital applications, including digital clocks, time
measurement, and frequency assessment.
Types of Counters:
1. Asynchronous counters
2. Synchronous counters

59. 1) Asynchronous Counters
The asynchronous counter is also called as Ripple counter and is made up of a series
of flip-flops.
• If the flip-flops do not receive the same clock signal, the counter is referred to as
asynchronous.
• Only the first flip-flop receives a clock signal from the system clock.
• The remaining flip-flops receive the clock signal from the previous stage flip-
output.

60. 2) Synchronous Counters
The synchronous counter is a counter also known as the parallel counter, operation is
fast if we compare it with asynchronous counters.
• The synchronous counter has a single global clock that drives each flip-flop,
allowing output to change in parallel.
• all of the flip flops clock inputs use the same source and produce the output at the
same time.
• The synchronous counter produces fewer errors than the asynchronous counter.

61. Other different types of Counters:
• Up Counter
• Down counter
• Bi-directional counter(Up-down counter)
• Decade counter
• Ring counter
• Cascade counter
• Johnson counter
• Modulus counter

62. Ring Counter:
A ring counter is defined as a special application of the serial-in serial-out
(SISO) shift register, where the output of the last flip-flop is connected to the
input of the first flip-flop.
• The ring counter contains only one logical 1 or 0 which it circulates. The total
cycle length is equal to the number of stages.
No of states = no of flip flop used

63. Truth table of ring Counter:
ORI CLK Q0 Q1 Q2 Q3
0 X 1 0 0 0
1 0 0 1 0 0
1 0 0 0 1 0
1 0 0 0 0 1
1 0 1 0 0 0
Note: The straight ring counter circulates the single 1 (or 0) bit around the ring.

64. Twisted Ring Counter(Johnson counter):
The Twisted Ring Counter refers to as a switch-tail ring Counter. Like the straight
ring counter, the outcome of the last flip-flop is passed to the first flip-flop as an
input.
• The twisted ring counter circulates a stream of 1's followed by 0 around the
ring.
• But in Johnson counter, the inverted outcome Q' of the last flip flop is passed
as an input. The remaining work of the Johnson counter is the same as a ring
counter.

65. Twisted Ring Counter(Johnson counter):
CLK Q0 Q1 Q2 Q3
X 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0
1 1 1 1 1
1 0 1 1 1
1 0 0 1 1
1 0 0 0 1
the number of states = 2 X the number of flip-flops.

66. Johnson Counter
Advantages:
• Johnson counter counts twice the number of states the ring counter can
count.
• The Johnson counter can also be designed by using D or JK flip flop.
Disadvantages:
• The Johnson counter is not able to count the states in a binary sequence.

67. Design of Synchronous counter:
• The synchronous counter uses the same clock signal from the same source and at
exactly the same time.
• Generally, it is constructed using either JK flip flop or T flip flop.
• Synchronous counters use edge-triggered flip-flops and change the state during the
next clock pulse.
Steps:
• Find the number of flip flops using 2n ≥ N, where N is the number of states and n is the
number of flip flops.
• Draw the state diagram of the counter.
• Draw the excitation table of the selected flip flop and determine the excitation table for
the counter.
• Use K-map to derive the flip flop input functions.
• Draw the Logic diagram.

68. Example: Design 3-bit synchronous up counter using JK flip flops.
1. Find the number of Flip-flop.
• A flip flop stores only one bit, hence for a 3 bit counter, 3 flip flops(n=3) are
needed to design the counter.
• Number of states = 2n
= 2^3 = 8 states(000, 001, 010, 011, 100, 101, 110, 111)
2. Draw the state diagram.

69. Example: Design 3-bit synchronous up counter using JK flip flops.
3.Obtain excitation table for the counter.

70. Example: Design 3-bit synchronous up counter using JK flip flops.
4. Map the Truth table of Counter with excitation table of the given Flip-flop.

71. Example: Design 3-bit synchronous up counter using JK flip flops.
5. Obtain the
expression for
every input of
Flip-flop.
• the present
inputs are
QC, QB, QA

72. Example: Design 3-bit synchronous up counter using JK flip flops.
6. Draw the logic diagram of the desired Counter.

73. MOD-N Counter:
A Modulus-M Counter is a counter in which N represents the number of states present.
• N = 2^n (2 raised to power n), where ‘n’ is the number of flip-flops required to design
the modulus-M counter.
• MOD Counters are cascaded counter circuits that count to a predetermined
modulus value before being reset.
• Modulus Counters, or simply MOD counters, are defined by the number of states they
will cycle through before returning to their original value. For instance, consider a 2-bit
counter that counts from 00 to 11.

74. Example: Design a Mod-6 synchronous up Counter.
Step 1: Find the number of flip flops.
• Mod-6 counter represents that the counter will have 6 states. Thus, N =6.
• The number of flip-flops used for counter design is determined using the
formula, 2n ≥ N.
• By trial and error method, the value of n is found to be 3. That is the number of flip-
flops, n = 3.
Hence the 6 counter states are 000, 001, 010, 011, 100, 101.
Let us choose the JK- flip flop to design the Mod-6 synchronous up counter.

75. Example: Design a Mod-6 synchronous up Counter.
Step 2: Draw state diagram for the counter.

76. Example: Design a Mod-6 synchronous up Counter.
Step 3: Obtain an excitation table for the counter..

77. Example: Design a Mod-6 synchronous up Counter.
Step 4: Map the truth table for desired counter with excitation table of JK-FF.

78. Example: Design a Mod-6 synchronous up Counter.
Step 5: Derive the expression for Inputs using the K-map.
00 01 11 10
0 0 1 x x
1 0 0 X X
QB QA
QC
JB
QC
00 01 11 10
0 1 x x 1
1 1 x X X
QB QA
JA
JC = QA.QB JB = QC’.QA
JA = 1

79. Example: Design a Mod-6 synchronous up Counter.
Step 2: Derive the expression for Inputs using the K-map.
00 01 11 10
0 x x x x
1 0 1 X X
QB QA
QC
Kc
00 01 11 10
0 x 1 1 x
1 x 1 X X
QB QA
KA
KC = QA
KA = 1
00 01 11 10
0 x 1 1 0
1 x x x x
QB QA
QC
KB
KB = QA

80. Step 6 : Draw the logic diagram of the counter
Example: Design a Mod-6 synchronous up Counter.

81. References:
• https://www.electronicshub.org/
• https://www.electrically4u.com/
• https://www.geeksforgeeks.org/
• https://electronics-course.com/
• https://www.electronics-tutorials.ws/
• https://www.javatpoint.com/counters-in-digital-electronics