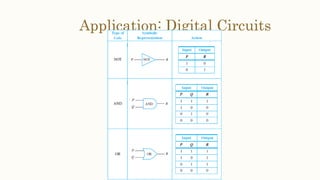
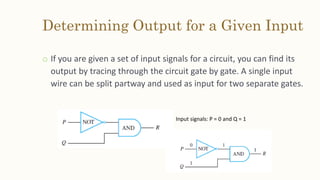
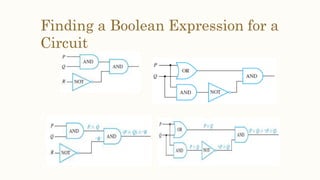
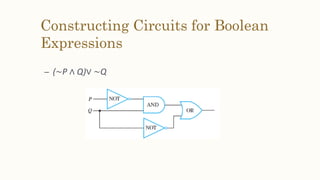
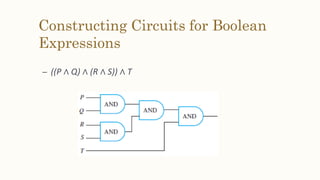
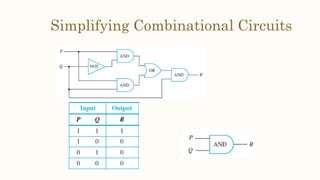
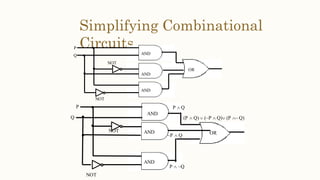
This document discusses the application of propositional logic to digital circuits. It describes how digital circuits use basic logic gates like NOT, AND and OR gates to process input signals and produce output signals. Complicated digital circuits can be constructed by combining these basic gates. The document also provides rules for building combinational circuits and techniques for simplifying circuits, such as constructing truth tables and using Boolean algebraic identities.

2. Application of Propositional Logic
o Propositional logic can be applied to the design of computer
hardware.
o A logic circuit (or digital circuit) receives input signals p1, p2, .
. . , pn, each a bit [either 0 (off) or 1 (on)], and produces
output signals s1, s2, . . . , sn, each a bit.
– Because of variety of digital circuits think basic circuits
black boxes.

3. Application: Digital Circuits
o The operation of a black box is completely specified by an
input/output table that lists all its possible input signals
together with their corresponding output signals.

4. Application: Digital Circuits
o Complicated digital circuits can be constructed from three
basic circuits, called gates,
o Three such circuits are known as NOT-, AND-, and OR-
gates.
o A NOT-gate (or inverter) is a circuit with one input signal
and one output signal. If the input signal is 1, the output
signal is 0. Conversely, if the input signal is 0, then the
output signal is 1.

5. Application: Digital Circuits
o An AND-gate is a circuit with two input signals and one
output signal. If both input signals are 1, then the output
signal is 1. Otherwise, the output signal is 0.
o An OR-gate also has two input signals and one output
signal. If both input signals are 0, then the output signal is
0. Otherwise, the output signal is 1.

6. Application: Digital Circuits

7. Rules for a Combinational Circuit
1. Never combine two input wires.
2. A single input wire can be split partway and used as
input for two separate gates.
3. An output wire can be used as input. No output of a
gate can eventually feed back into that gate.

8. Determining Output for a Given Input
o If you are given a set of input signals for a circuit, you can find its
output by tracing through the circuit gate by gate. A single input
wire can be split partway and used as input for two separate gates.
Input signals: P = 0 and Q = 1

9. Constructing the Input/Output Table for
a Circuit

10. Finding a Boolean Expression for a
Circuit

11. Constructing Circuits for Boolean
Expressions
– (∼P ∧ Q)∨ ∼Q

12. Constructing Circuits for Boolean
Expressions
– ((P ∧ Q) ∧ (R ∧ S)) ∧ T

13. Simplifying Combinational Circuits

14. Simplifying Combinational Circuits
– Two digital logic circuits are equivalent if, and only if, their
input/output tables are identical.
((P ∧ ∼Q) ∨ (P ∧ Q)) ∧ Q
≡ (P ∧ (∼Q ∨ Q)) ∧ Q by the distributive law
≡ (P ∧ (Q ∨ ∼Q)) ∧ Q by the commutative
law for ∨
≡ (P ∧ t) ∧ Q by the negation law
≡ P ∧ Q by the identity law.

15. Simplifying Combinational
Circuits
AND
AND
AND
OR
P
Q
NOT
NOT
AND
AND
AND
OR
P
Q
NOT
NOT
P Ù Q
~P Ù Q
P Ù ~Q
(P Ù Q) Ú (~P Ù Q)Ú (P Ù~ Q)

16. Simplifying Combinational
Circuits
STATEMENT REASON
(P Ù Q) Ú(~P Ù Q) Ú (P Ù~ Q)
 (P Ù Q) Ú (~P Ù Q) Ú (P Ù~ Q)
 (P Ú ~P) Ù QÚ (P Ù~ Q) Distributive law
 t ÙQ Ú (P Ù~Q) Negation law
 Q Ú (P Ù~Q) Identity law
 (QÚP) Ù (Q Ú ~Q) Distributive law
 (Q Ú P) Ù t Negation law
 (Q Ú P) Ù t
 Q Ú P Identity law
 P Ú Q Commutative law
Thus (P Ù Q) Ú(~P Ù Q) Ú (P Ù~ Q)  P Ù Q
Accordingly, the two circuits are equivalent

17. NAND and NOR Gates
o A NAND-gate is a single gate that acts like an AND-gate followed by a NOT-
gate.
– Thus the output signal of a NAND-gate is 0 when, and only when, both input signals are 1,
o A NOR-gate acts like an OR-gate followed by a NOT-gate.
– The output signal for a NOR-gate is 1 when, and only when, both input signals are 0.
o The logical symbols corresponding to these gates are | (for NAND) and ↓ (for
NOR), where | is called a Sheffer stroke and ↓ is called a Peirce arrow .

18. NAND and NOR Gates
o P | Q ≡ ∼(P ∧ Q) and P ↓ Q ≡ ∼(P ∨ Q).