Downloaded 54 times
![Quadruple 2-to-1 Line Mux
F[3:0]
SEL
En
2-to-12-to-1
MuxMux
(4-bit bus)(4-bit bus)
A3..0
B3..0
A[3:0]
B[3:0]
EnEn SELSEL F[3:0]F[3:0]
0 X 0000
1 0 A[3:0]
1 1 B[3:0]](https://image.slidesharecdn.com/lec10-mux-150829105741-lva1-app6891/75/Lec10-Intro-to-Computer-Engineering-by-Hsien-Hsin-Sean-Lee-Georgia-Tech-Multiplexors-26-2048.jpg)
![Quadruple 2-to-1 Line Mux
EnEn SELSEL F[3:0]F[3:0]
0 X 0000
1 0 A[3:0]
1 1 B[3:0]
SEL
B0
A0
F0
B3
A3
F3
B1
A1
F1
B2
A2
F2
En
Fx=Ax·En·SEL+Bx·En·SEL](https://image.slidesharecdn.com/lec10-mux-150829105741-lva1-app6891/75/Lec10-Intro-to-Computer-Engineering-by-Hsien-Hsin-Sean-Lee-Georgia-Tech-Multiplexors-27-2048.jpg)
Uploaded byHsien-Hsin Sean Lee, Ph.D.
Lec10 Intro to Computer Engineering by Hsien-Hsin Sean Lee Georgia Tech -- Multiplexors
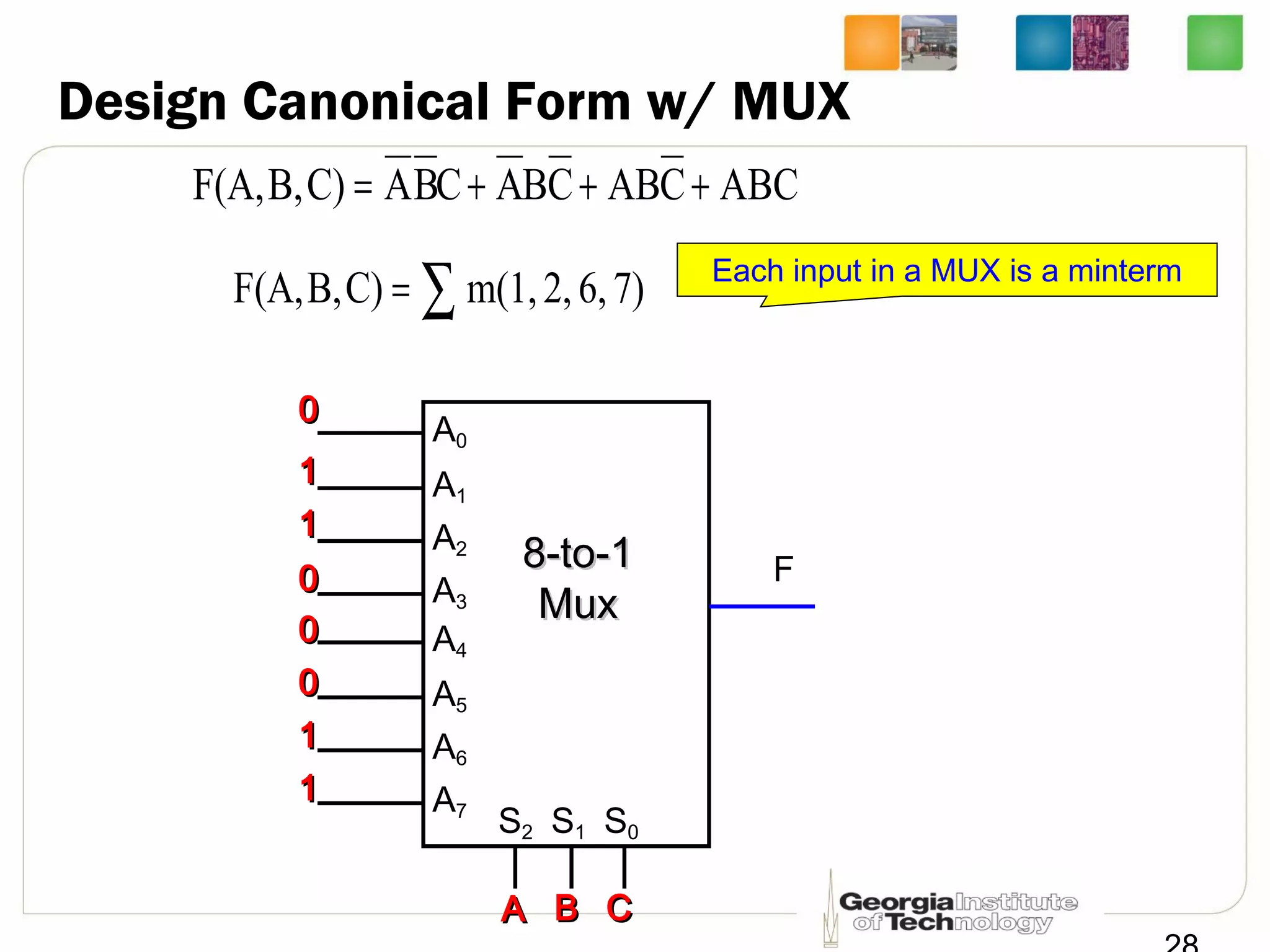
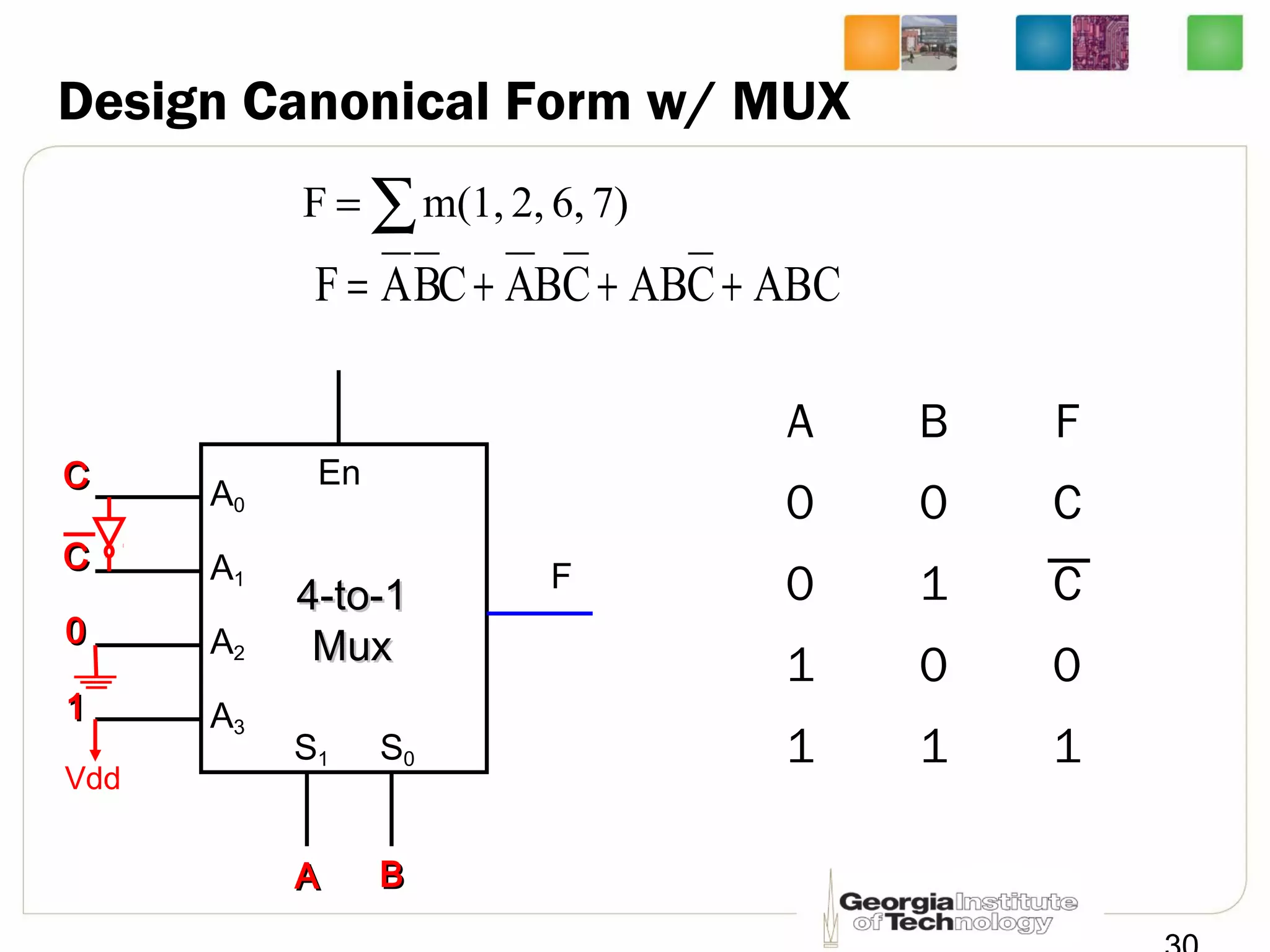
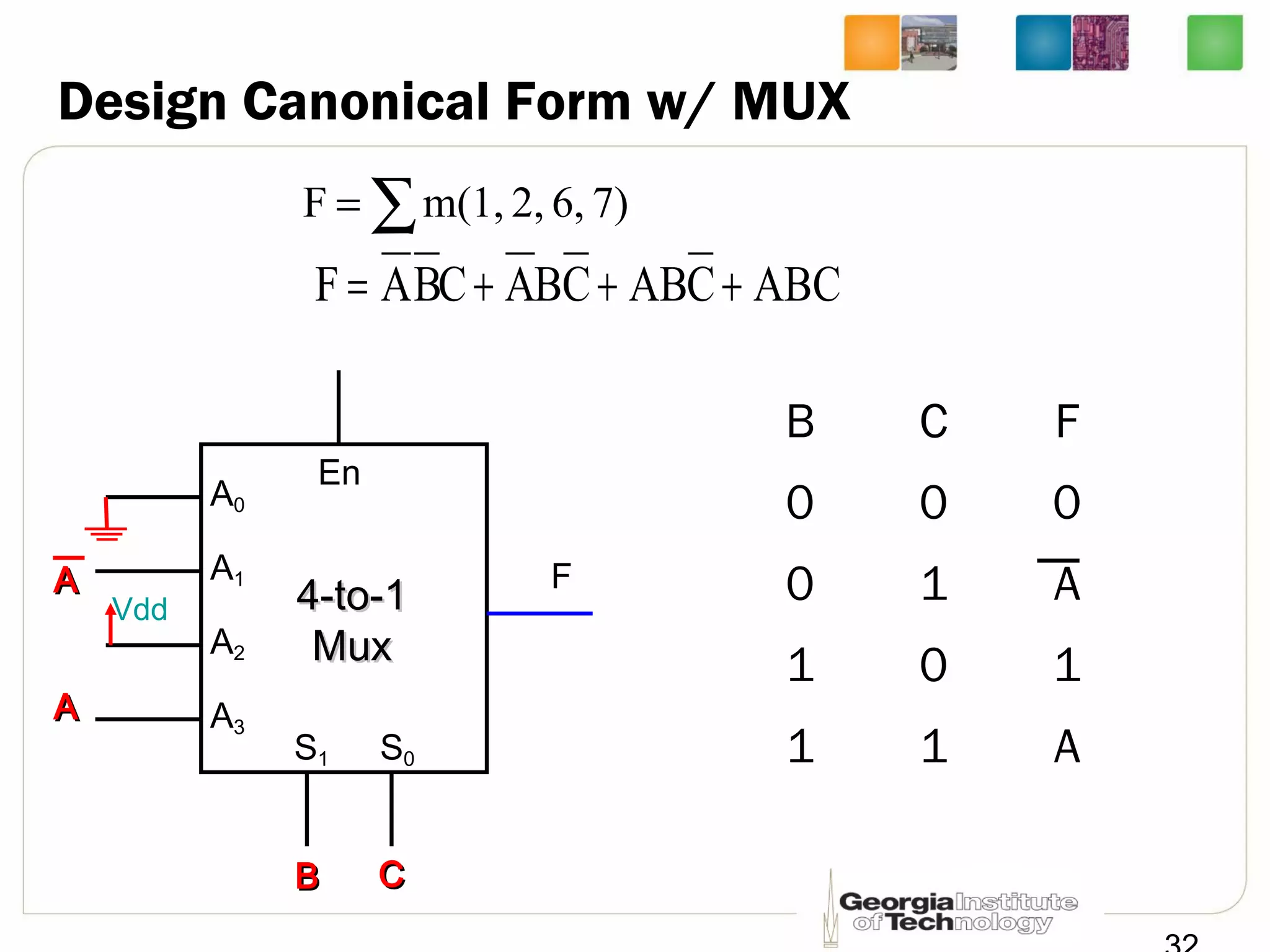
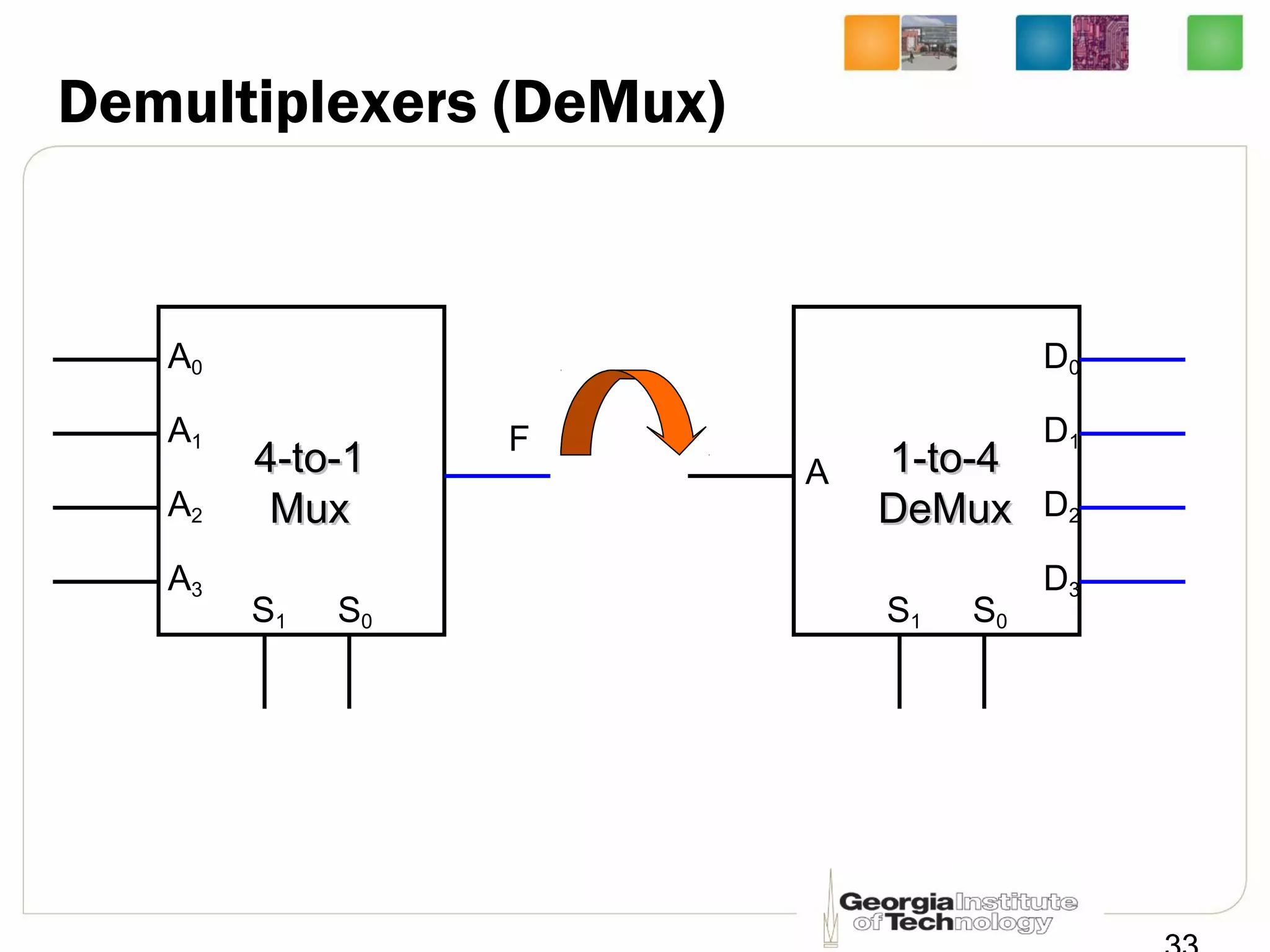
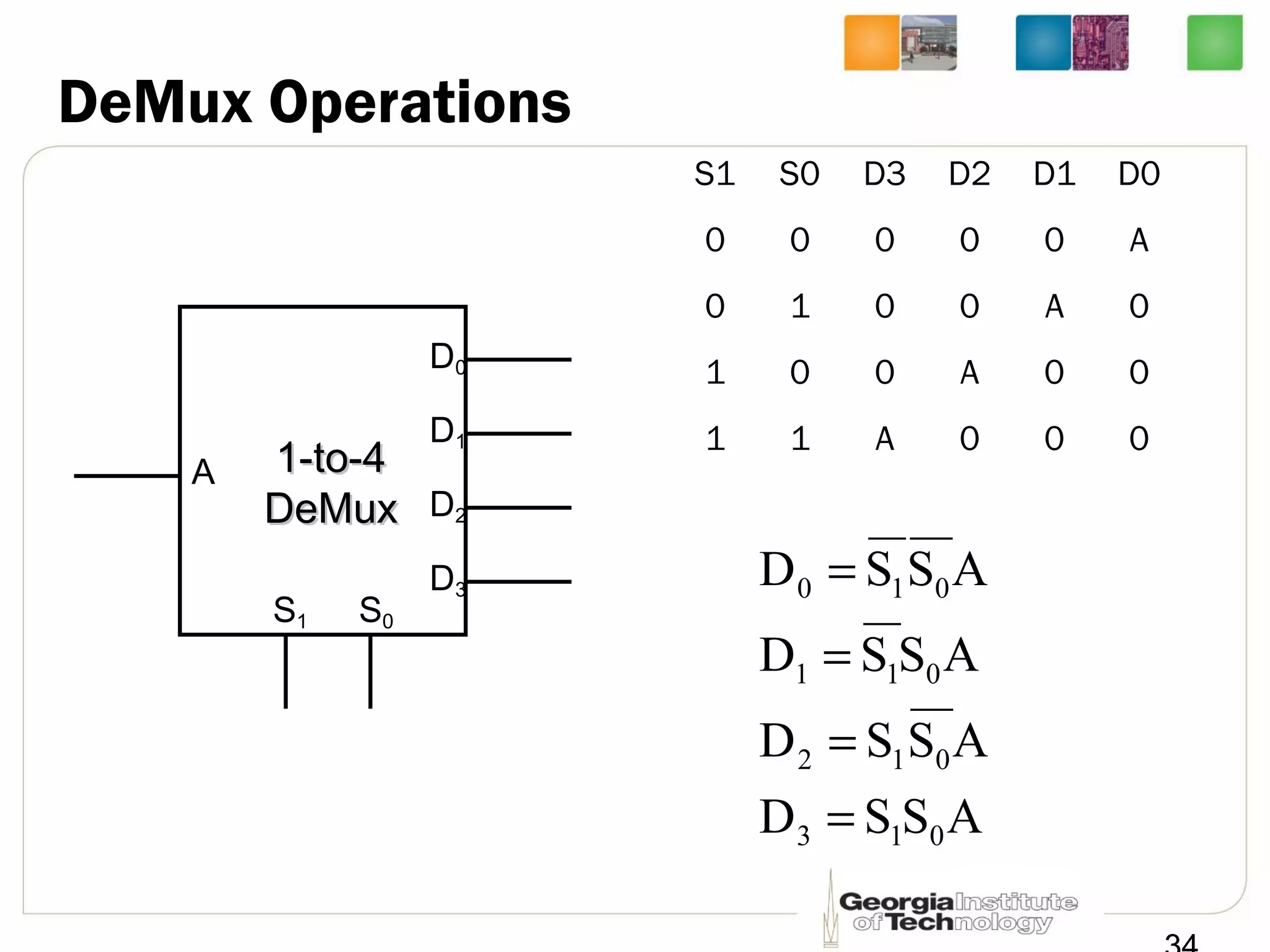
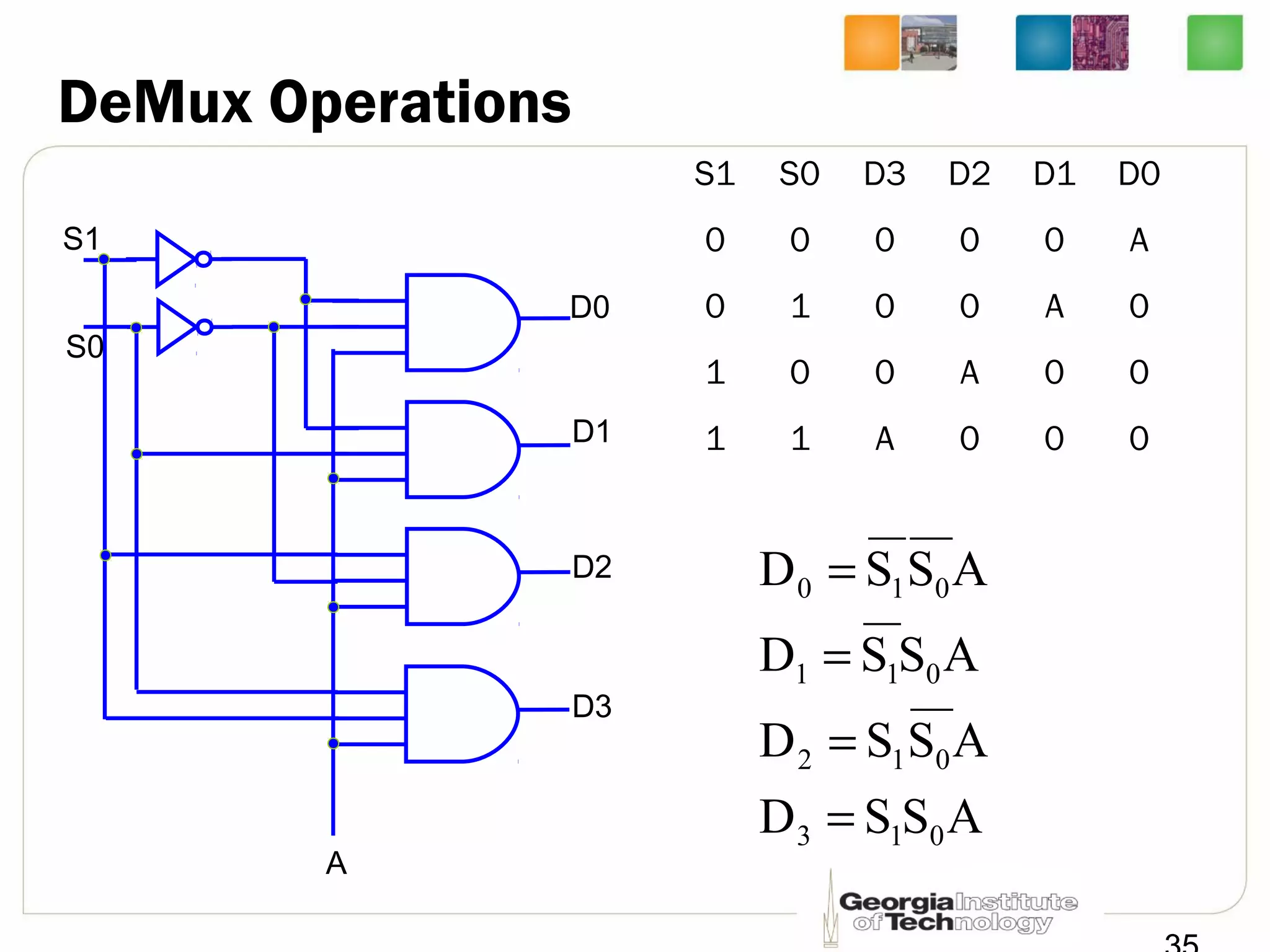
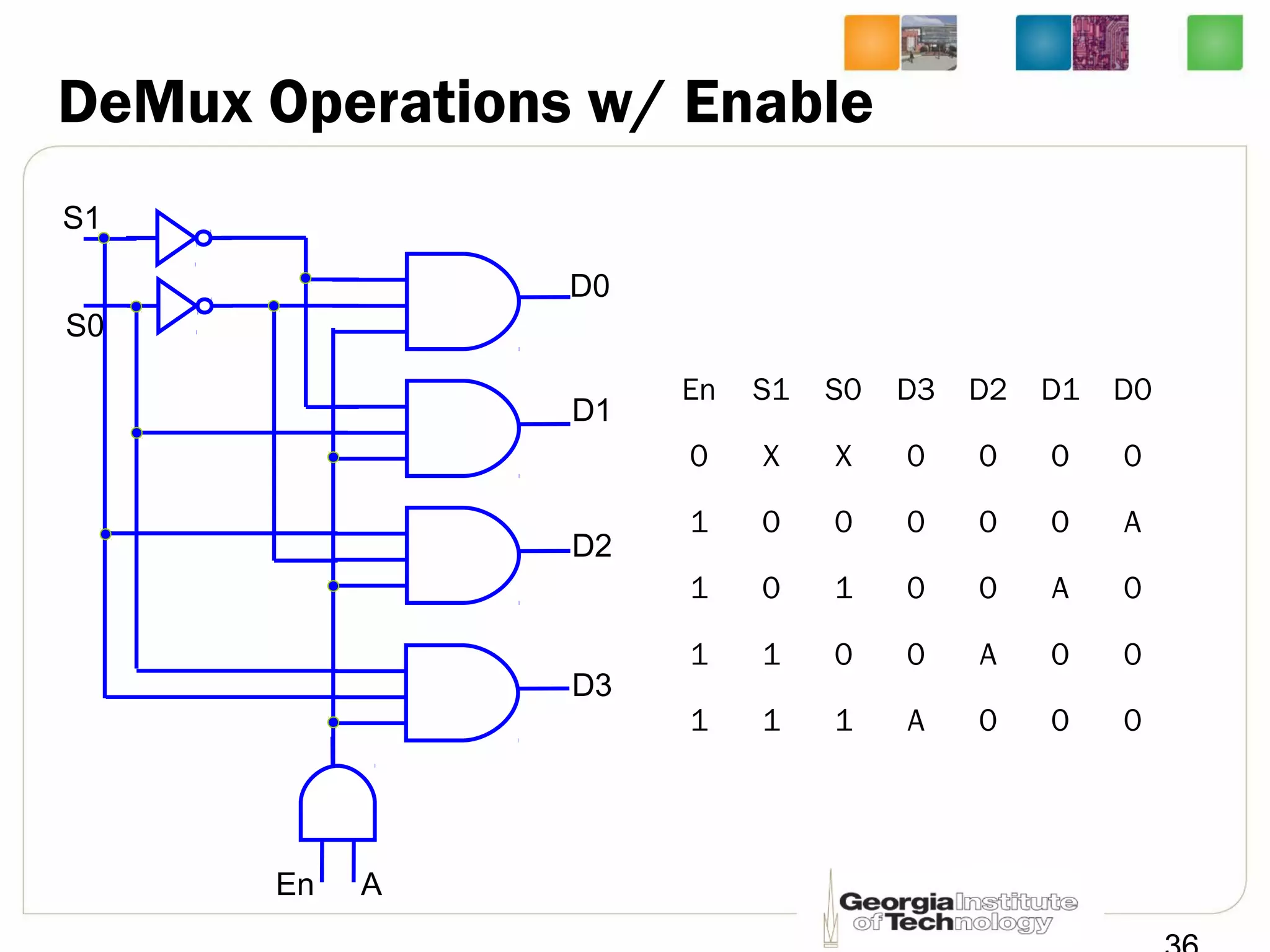
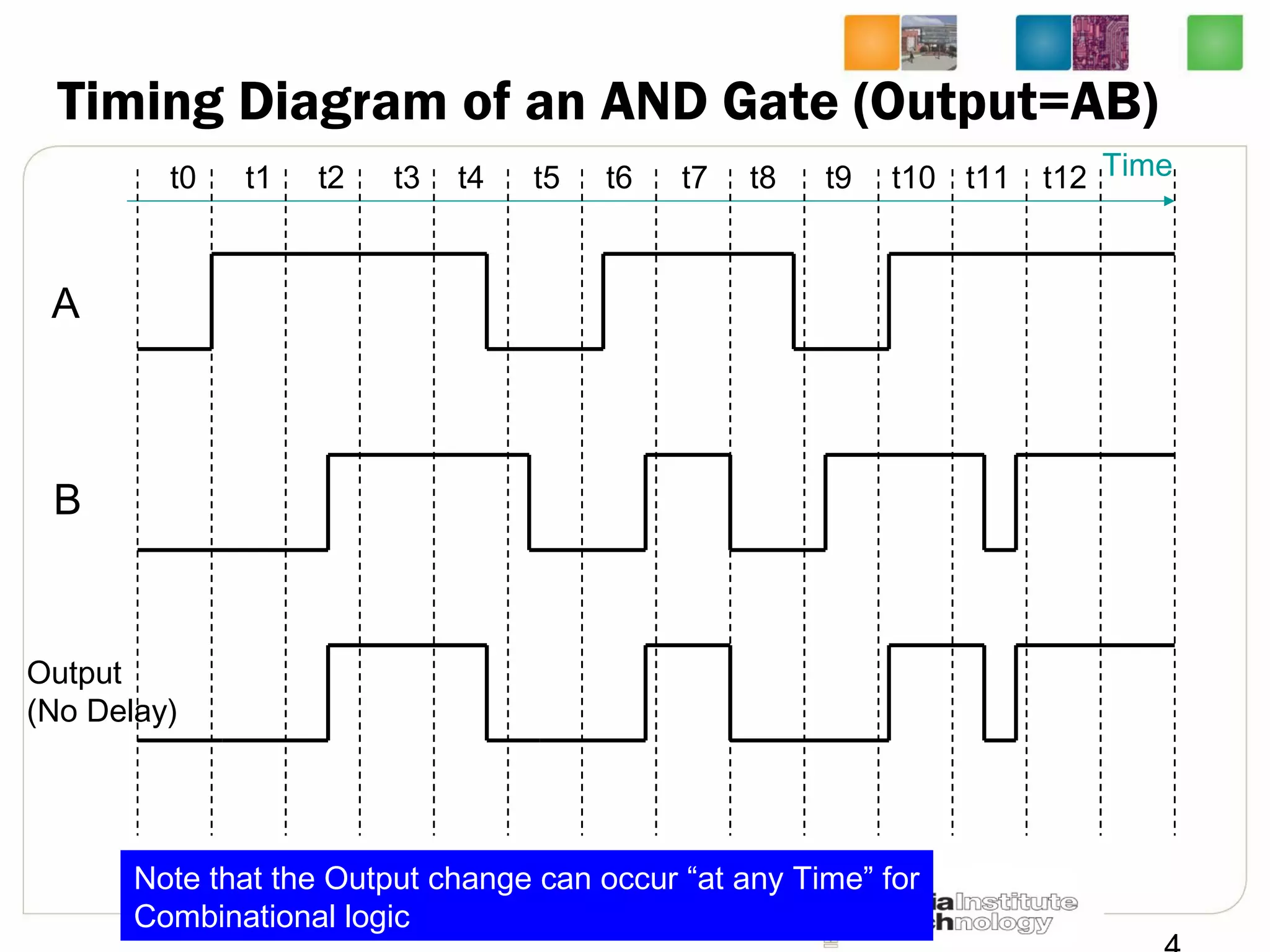
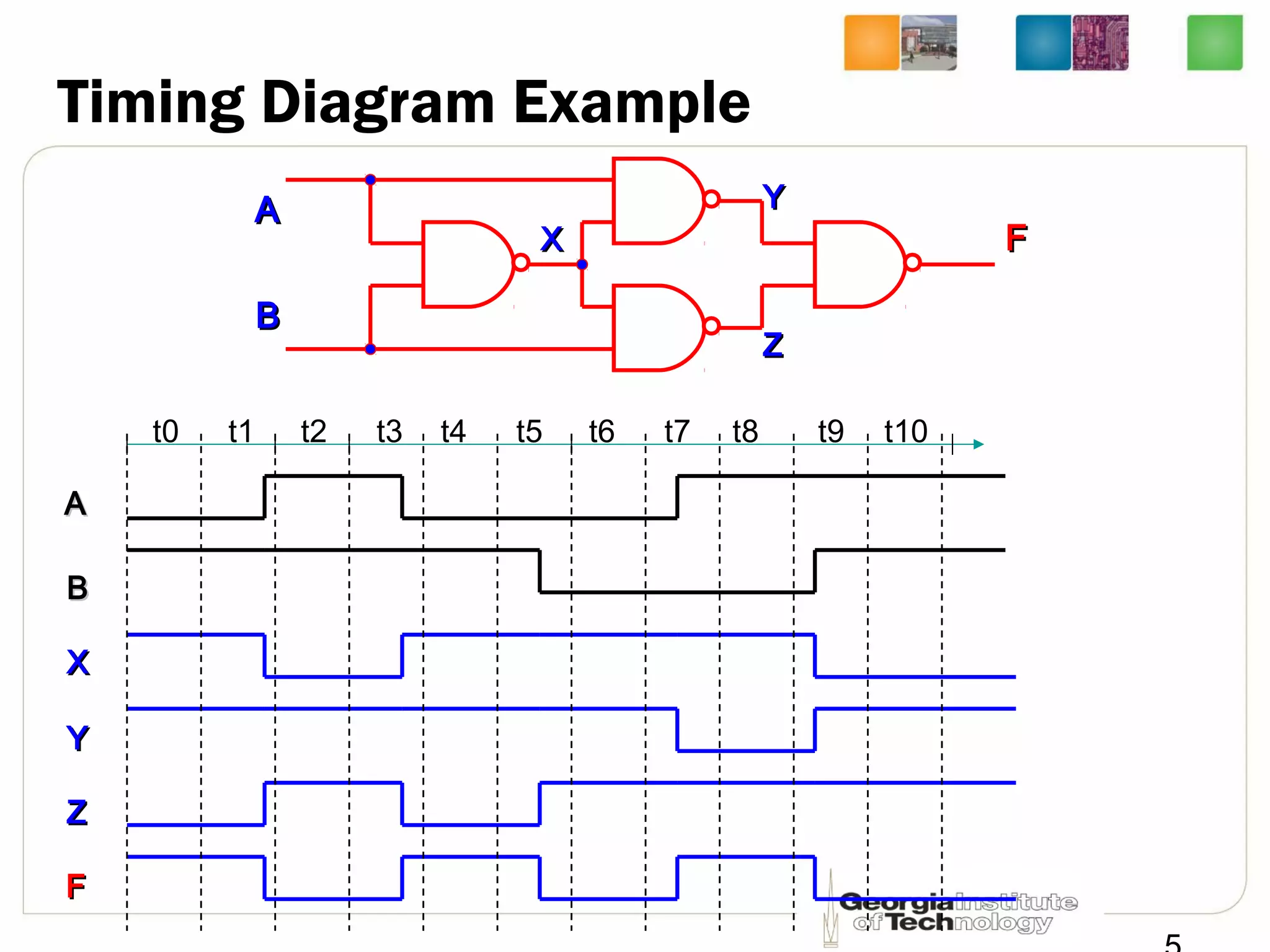
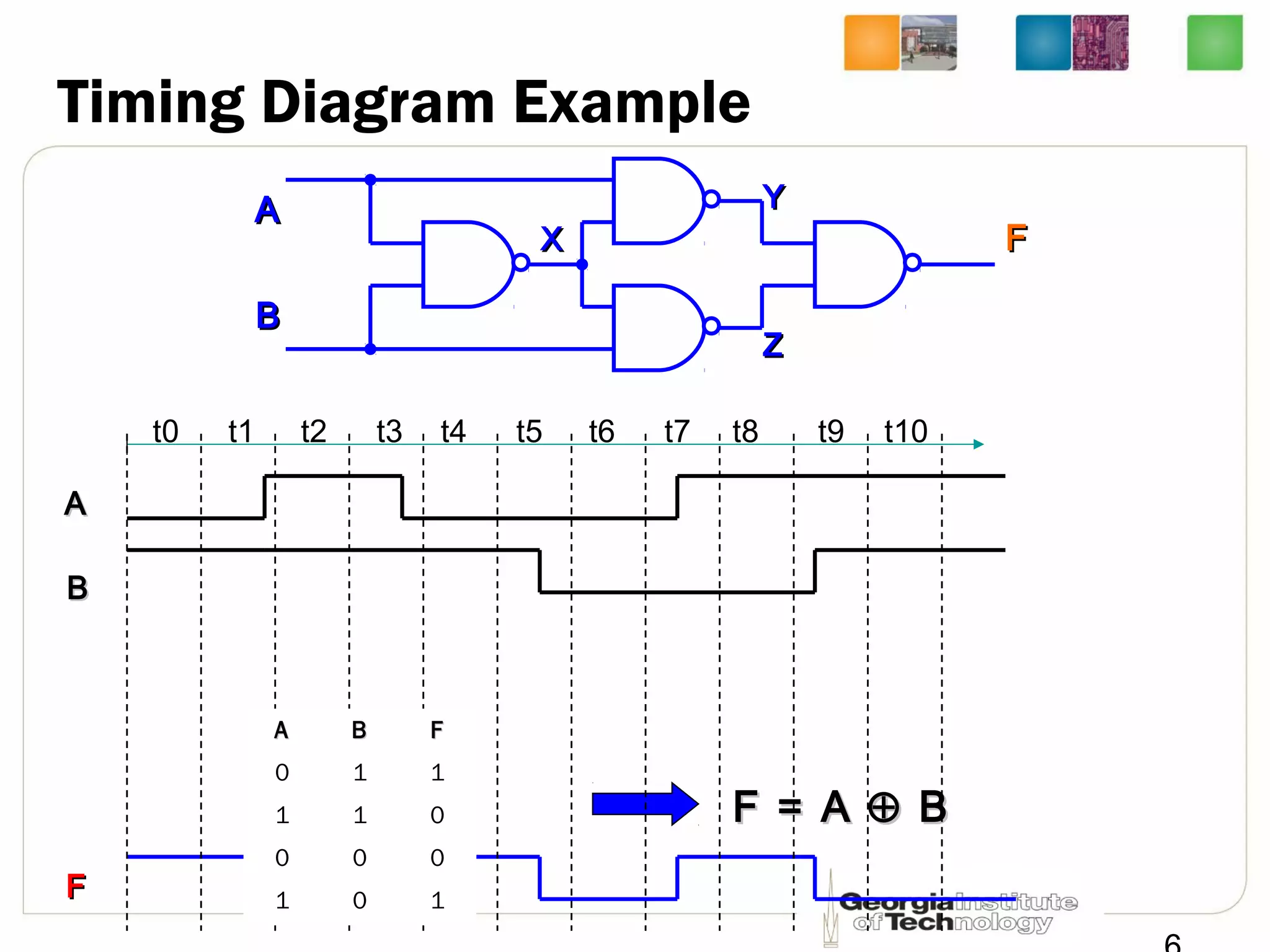
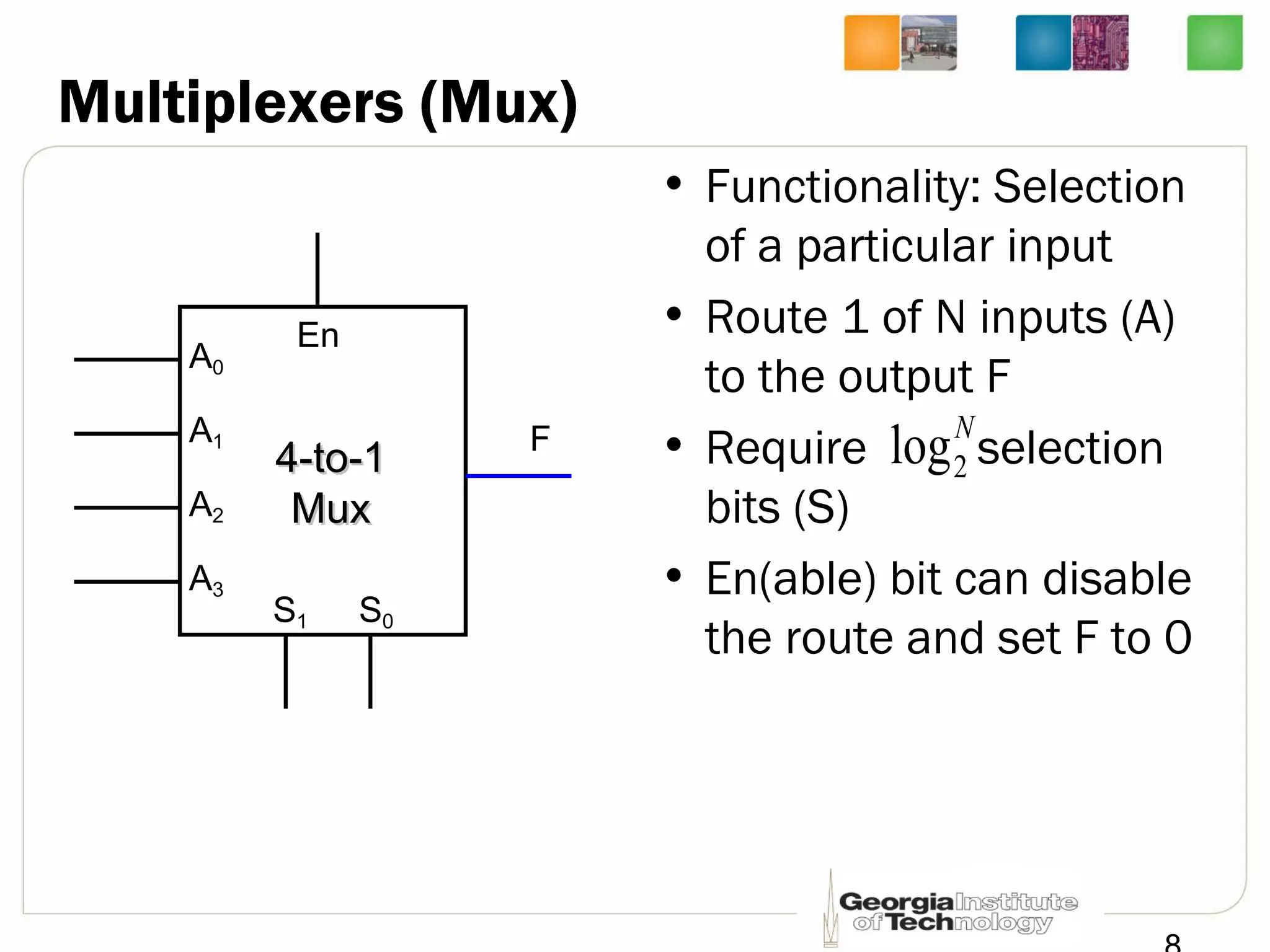
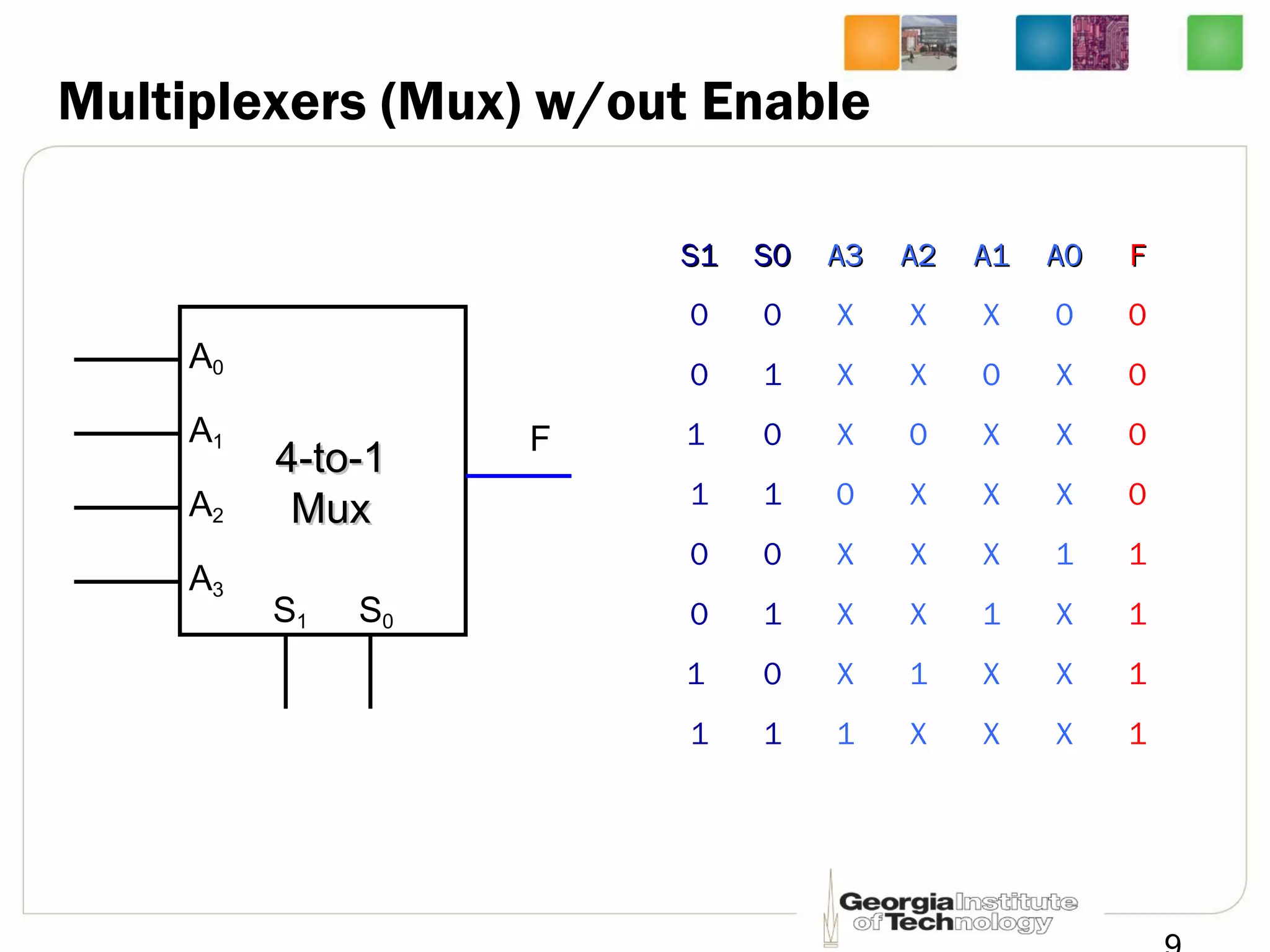
This document provides a summary of a lecture on building blocks for combinational logic, including timing diagrams, multiplexers, and demultiplexers. Timing diagrams are used to describe the functionality of logic circuits over time as a series of waveforms. Multiplexers are used to select one of several input signals to pass to the output based on selection bits. Demultiplexers are the inverse, distributing an input signal to one of several outputs based on the selection bits. Transmission gates can be used to implement multiplexers with enable inputs to disable the output.
More Related Content
Similar to Lec10 Intro to Computer Engineering by Hsien-Hsin Sean Lee Georgia Tech -- Multiplexors
Lec10 Intro to Computer Engineering by Hsien-Hsin Sean Lee Georgia Tech -- Multiplexors
- 1. ECE2030 Introduction to ComputerEngineering Lecture 10: Building Blocks for Combinational Logic (1) Timing Diagram, Mux/DeMux Prof. Hsien-Hsin Sean LeeProf. Hsien-Hsin Sean Lee School of Electrical and Computer EngineeringSchool of Electrical and Computer Engineering Georgia TechGeorgia Tech
- 2. Combinational Logic • Outputs,“at any time”, are determined by the input combination • When input changed, output changed immediately – Real circuits is imperfect and have “propagation delay” • A combinational circuit – Performs logic operations that can be specified by a set of Boolean expressions – Can be built hierarchically Combinational circuits N inputs M outputs
- 3. Timing Diagram • Describethe functionality of a logic circuit across time • Represented by a waveform • For combinational logic, Output is a function of inputs
- 4. Timing Diagram ofan AND Gate (Output=AB) Time A B Output (No Delay) t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 Note that the Output change can occur “at any Time” for Combinational logic
- 5. Timing Diagram Example XX YY ZZ FF AA BB AA BB XX YY ZZ FF t0t1 t2 t3 t4 t5 t6 t7 t8 t9 t10
- 6. Timing Diagram Example XX YY ZZ FF AA BB AA BB FF AABB FF 0 1 1 1 1 0 0 0 0 1 0 1 F = AF = A ⊕⊕ BB t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10
- 7. Combinational Logic • Outputs,“at any time”, are determined by the input combination • We will discuss – Multiplexers / De-Multiplexers – Decoders / Encoders – Comparators – Parity Checkers / Generators – Binary Adders / Subtractors – Integer Multipliers Combinational circuits N inputs M outputs
- 8. Multiplexers (Mux) • Functionality:Selection of a particular input • Route 1 of N inputs (A) to the output F • Require selection bits (S) • En(able) bit can disable the route and set F to 0 F A0 A1 A2 A3 S1 S0 En 4-to-14-to-1 MuxMux N 2log
- 9. Multiplexers (Mux) w/outEnable F A0 A1 A2 A3 S1 S0 4-to-14-to-1 MuxMux S1S1 S0S0 A3A3 A2A2 A1A1 A0A0 FF 0 0 X X X 0 0 0 1 X X 0 X 0 1 0 X 0 X X 0 1 1 0 X X X 0 0 0 X X X 1 1 0 1 X X 1 X 1 1 0 X 1 X X 1 1 1 1 X X X 1
- 10. Multiplexers (Mux) w/outEnable S1S1 S0S0 FF 0 0 A0 0 1 A1 1 0 A2 1 1 A3 F A0 A1 A2 A3 S1 S0 4-to-14-to-1 MuxMux 30121101001 ASSAS0SASSASSF +++=
- 11. Logic Diagram ofa 4-to-1 Mux 30121101001 ASSAS0SASSASSF +++= S1 S0 A0 A1 A2 A3 F
- 12. Multiplexers (Mux) w/Enable EnEn S1S1 S0S0 FF 0 X X 0 1 0 0 A0 1 0 1 A1 1 1 0 A2 1 1 1 A3 30121101001 30121101001 ASEnSAS0EnSASSEnASSEn )ASSAS0SASSASS(EnF +++= +++⋅= F A0 A1 A2 A3 S1 S0 En 4-to-14-to-1 MuxMux
- 13. 4-to-1 Mux w/Enable Logic )ASSAS0SASSASS(EnF 30121101001 +++⋅= S1 S0 A0 A1 A2 A3 F En
- 14. 4-to-1 Mux w/Enable Logic 30121101001 ASEnSAS0EnSASSEnASSEnF +++= S1 S0 A0 A1 A2 A3 F En Reduce one Gate Delay by using 4-input AND gate for the 2nd level En
- 15. 4-to-1 Mux usingTransmission Gates A0 A1 A2 A3 S0 S1 F S1S1 S0S0 FF 0 0 A0 0 1 A1 1 0 A2 1 1 A3
- 16. 4-to-1 Mux usingTransmission Gates A0 A1 A2 A3 S0=0 S1 F S1S1 S0S0 FF 0 0 A0 0 1 A1 1 0 A2 1 1 A3 A0 A2
- 17. 4-to-1 Mux usingTransmission Gates A0 A1 A2 A3 F S1S1 S0S0 FF 0 0 A0 0 1 A1 1 0 A2 1 1 A3 A0 A2 A0 A2 S0=0 S1=0
- 18. 4-to-1 Mux usingTransmission Gates A0 A1 A2 A3 S0=1 S1 F S1S1 S0S0 FF 0 0 A0 0 1 A1 1 0 A2 1 1 A3 A0 A2
- 19. 4-to-1 Mux usingTransmission Gates A0 A1 A2 A3 F S1S1 S0S0 FF 0 0 A0 0 1 A1 1 0 A2 1 1 A3 A0 A2 A1 A3 S0=1 S1=1
- 20. 4-to-1 Mux usingTransmission Gates with Enable (F=0 when En=0) A0 A1 A2 A3 A0 A2 S0=1 S1=1 EnEn S1S1 S0S0 FF 0 X X 0 1 0 0 A0 1 0 1 A1 1 1 0 A2 1 1 1 A3 F En
- 21. 4-to-1 Mux usingTransmission Gates with Enable (F=Z when En=0) A0 A1 EnEn S1S1 S0S0 FF 0 X X Z 1 0 0 A0 1 0 1 A1 1 1 0 A2 1 1 1 A3 En=0 X=0 Y=1 (To disable both TG) XX YY X=En· S0 En=1 X=S0 Y=S0 Y=En + En·S0 = En + S0
- 22. 4-to-1 Mux usingTransmission Gates with Enable (F=Z when En=0) A0 A1 EnEn S1S1 S0S0 FF 0 X X Z 1 0 0 A0 1 0 1 A1 1 1 0 A2 1 1 1 A3 XX YY X=En· S0 En S0 Y=En + En·S0 = En + S0 XX YY
- 23. 4-to-1 Mux usingTransmission Gates with Enable (F=Z when En=0) A0 A1 EnEn S1S1 S0S0 FF 0 X X Z 1 0 0 A0 1 0 1 A1 1 1 0 A2 1 1 1 A3 X=En· S0 En S0 A2 A3 Y=En + En·S0 = En + S0
- 24. 4-to-1 Mux usingTransmission Gates with Enable (F=Z when En=0) A0 A1 En S0 A2 A3 F EnEn S1S1 S0S0 FF 0 X X Z 1 0 0 A0 1 0 1 A1 1 1 0 A2 1 1 1 A3 S1
- 25. Simplified 4-to-1 Muxusing TGs with Enable (F=Z when En=0) S1 F EnEn S1S1 S0S0 FF 0 X X Z 1 0 0 A0 1 0 1 A1 1 1 0 A2 1 1 1 A3 A0 A1 A2 A3 A0 A2 S0 En Only Disable the 2nd level X=En· S0 XX YY Y=En + En·S0 = En + S0
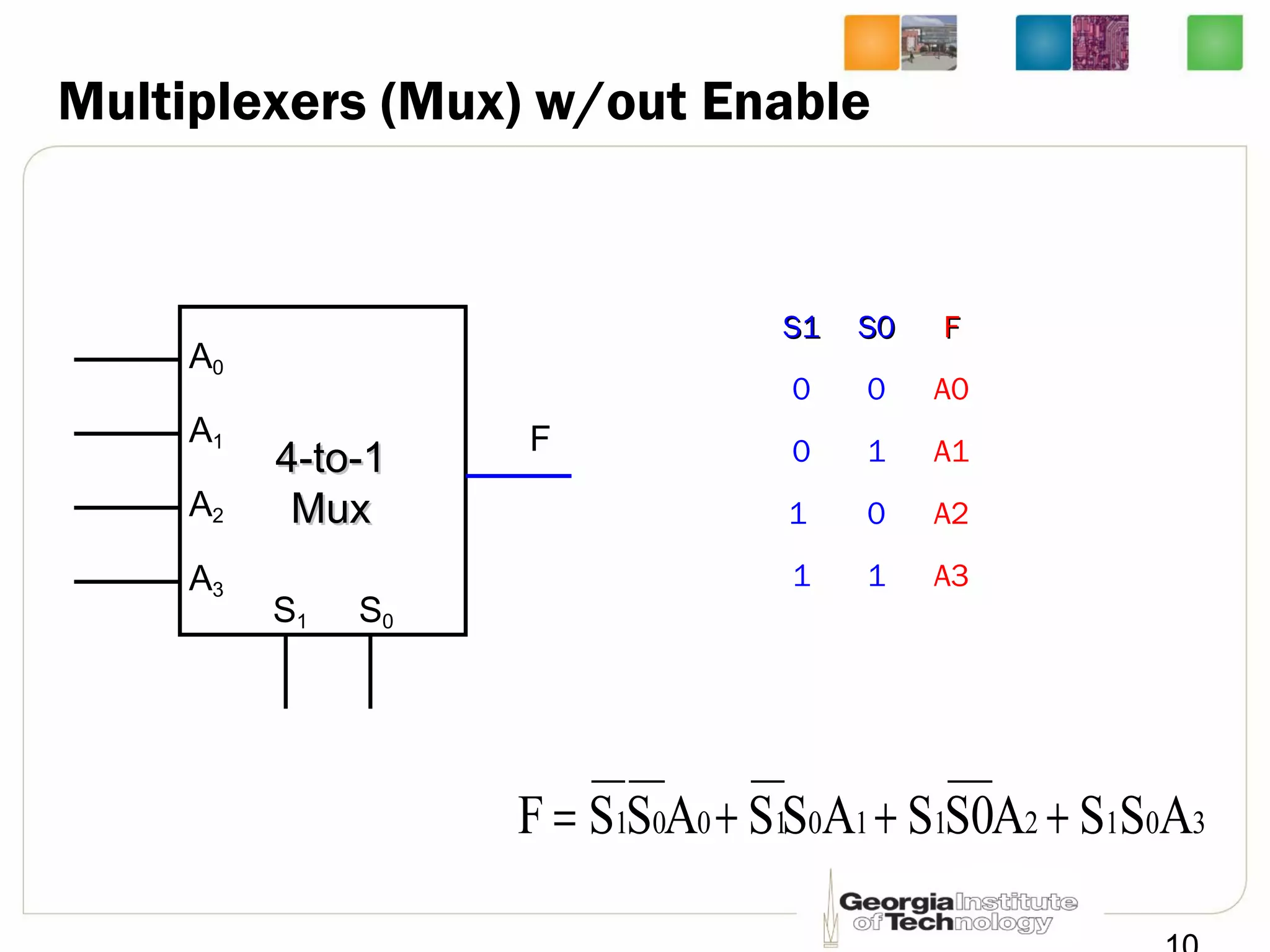
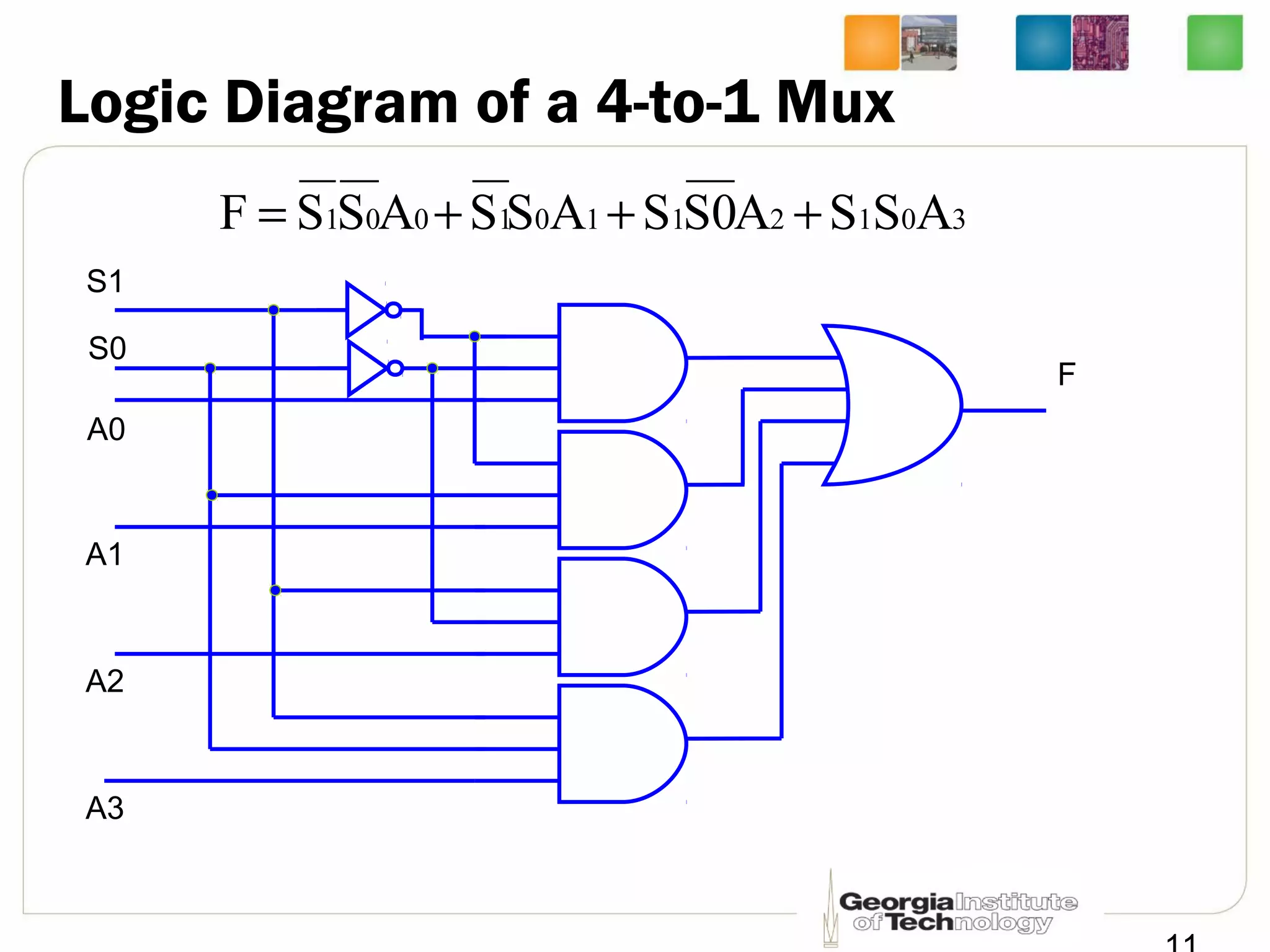
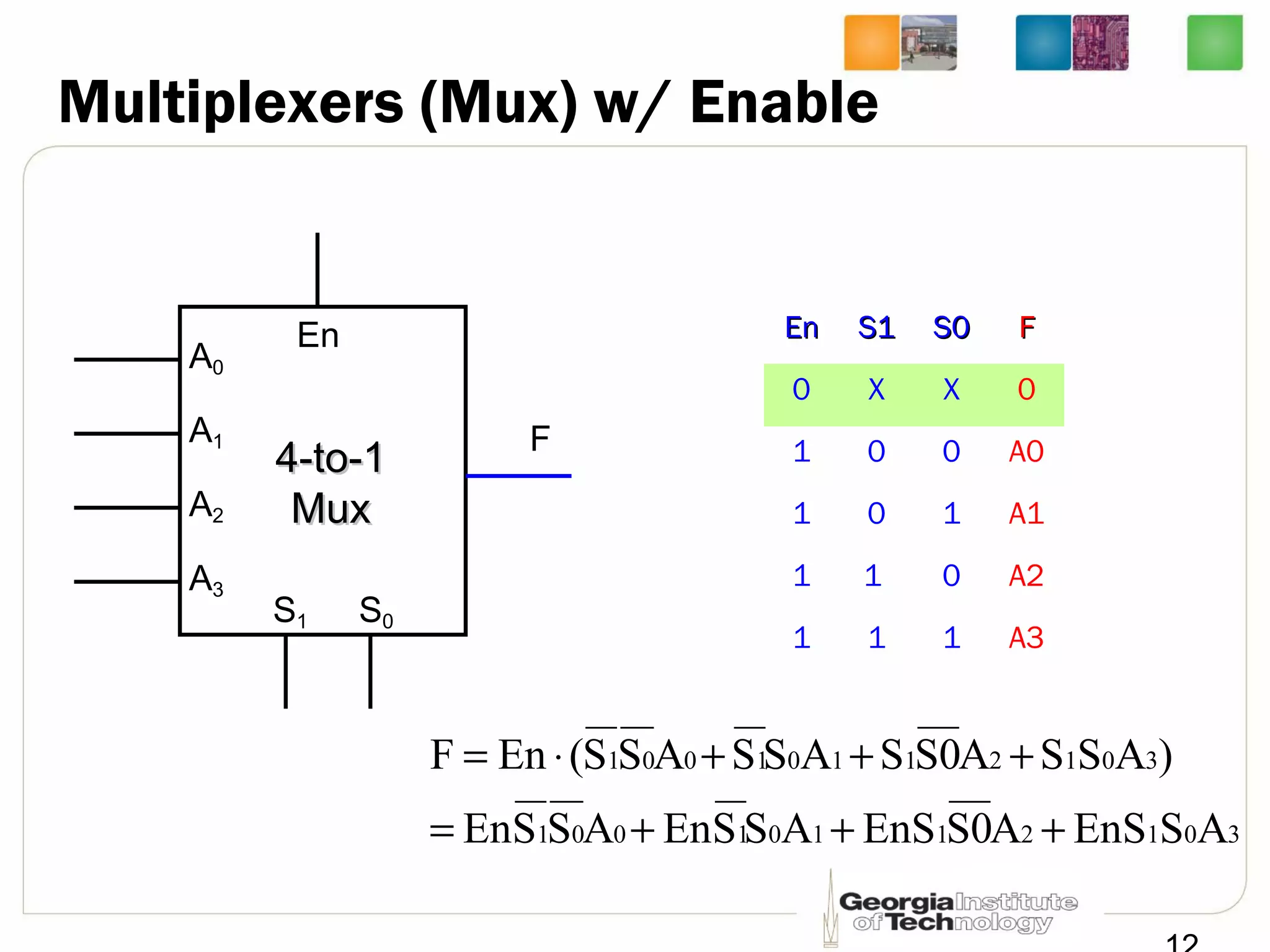
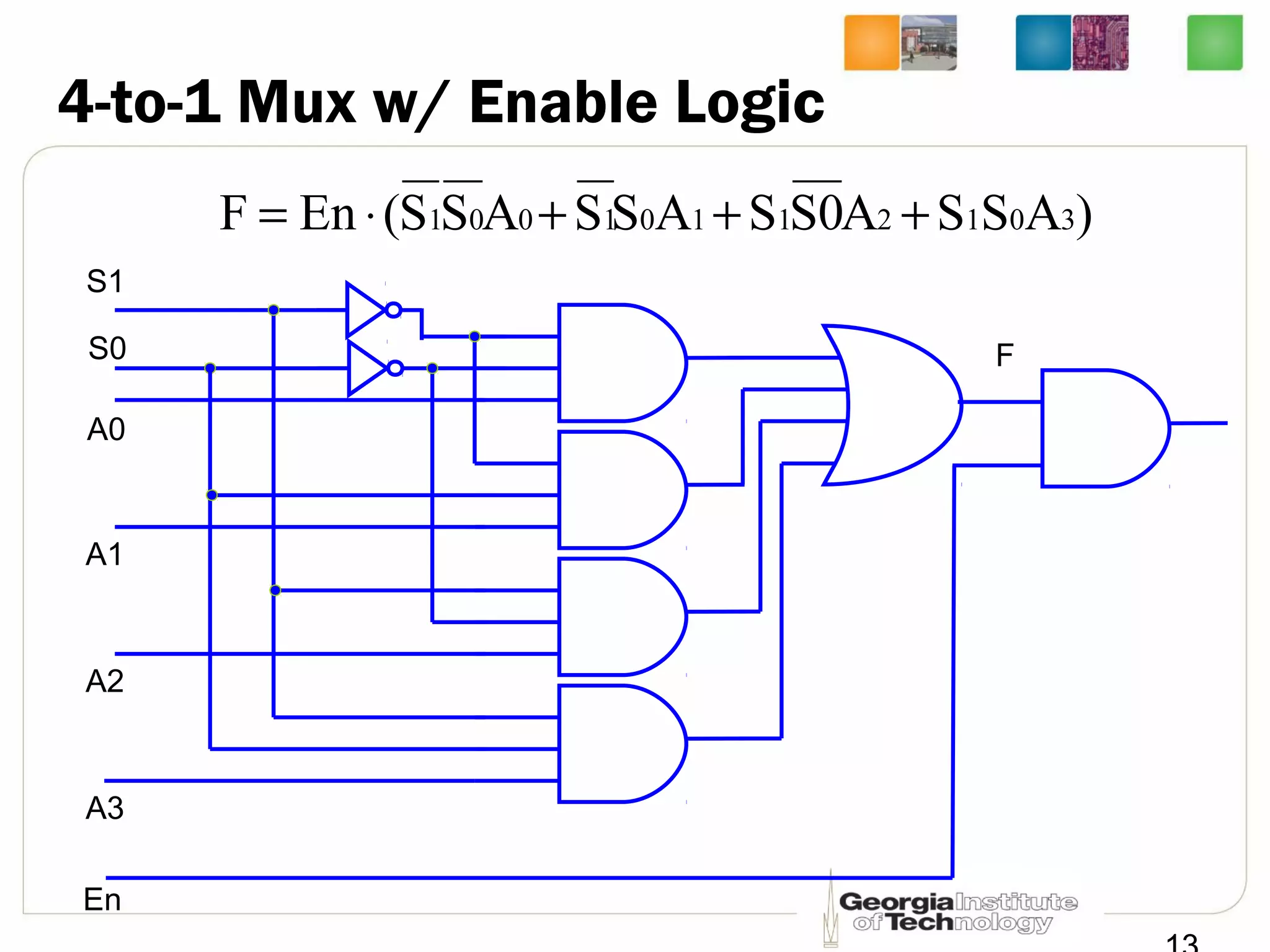
- 26. Quadruple 2-to-1 LineMux F[3:0] SEL En 2-to-12-to-1 MuxMux (4-bit bus)(4-bit bus) A3..0 B3..0 A[3:0] B[3:0] EnEn SELSEL F[3:0]F[3:0] 0 X 0000 1 0 A[3:0] 1 1 B[3:0]
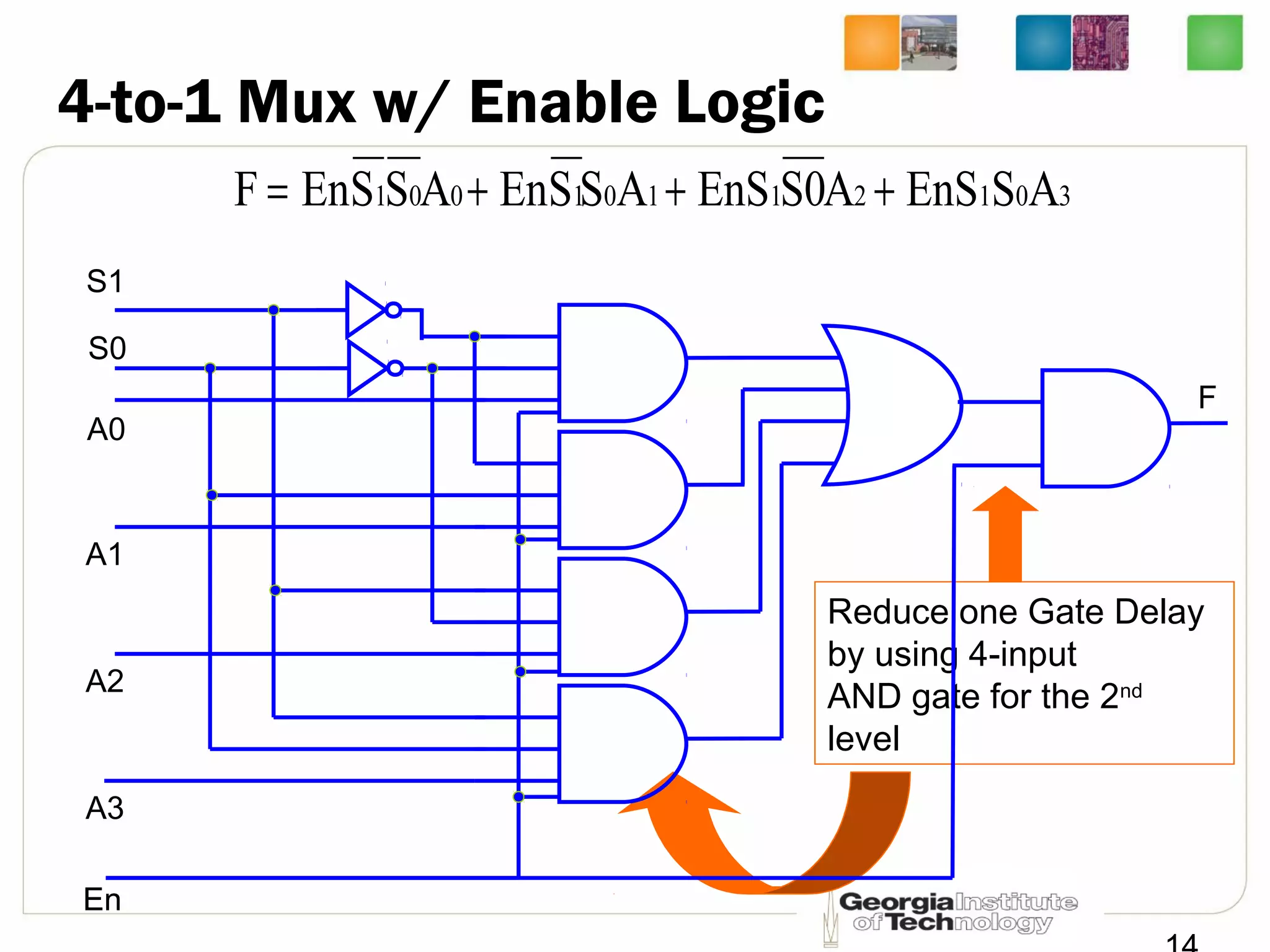
- 27. Quadruple 2-to-1 LineMux EnEn SELSEL F[3:0]F[3:0] 0 X 0000 1 0 A[3:0] 1 1 B[3:0] SEL B0 A0 F0 B3 A3 F3 B1 A1 F1 B2 A2 F2 En Fx=Ax·En·SEL+Bx·En·SEL
- 28. Design Canonical Formw/ MUX ∑= 7)6,2,m(1,C)B,F(A, ABCCABCBACBAC)B,F(A, +++= F A0 A1 A2 A3 S1 S0 8-to-18-to-1 MuxMux S2 A4 A5 A6 A7 00 00 00 00 11 11 11 11 Each input in a MUX is a minterm AA BB CC
- 29. Design Canonical Formw/ MUX ∑= 7)6,2,m(1,C)B,F(A, ABCCABCBACBAF +++= A B F 0 0 0 1 1 0 1 1
- 30. Design Canonical Formw/ MUX ∑= 7)6,2,m(1,F ABCCABCBACBAF +++= A B F 0 0 C 0 1 C 1 0 0 1 1 1 F A0 A1 A2 A3 S1 S0 En 4-to-14-to-1 MuxMux AA BB CC CC 00 11 Vdd
- 31. Design Canonical Formw/ MUX ∑= 7)6,2,m(1,F ABCCABCBACBAF +++= B C F 0 0 0 1 1 0 1 1
- 32. Design Canonical Formw/ MUX ∑= 7)6,2,m(1,F ABCCABCBACBAF +++= B C F 0 0 0 0 1 A 1 0 1 1 1 A F A0 A1 A2 A3 S1 S0 En 4-to-14-to-1 MuxMux BB CC AA AA Vdd
- 33. Demultiplexers (DeMux) F A0 A1 A2 A3 S1 S0 4-to-14-to-1 MuxMux A D0 D1 D2 D3 S1S0 1-to-41-to-4 DeMuxDeMux
- 34. DeMux Operations S1 S0D3 D2 D1 D0 0 0 0 0 0 A 0 1 0 0 A 0 1 0 0 A 0 0 1 1 A 0 0 0 A D0 D1 D2 D3 S1 S0 1-to-41-to-4 DeMuxDeMux ASSD ASSD ASSD ASSD 013 012 011 010 = = = =
- 35. DeMux Operations S1 S0D3 D2 D1 D0 0 0 0 0 0 A 0 1 0 0 A 0 1 0 0 A 0 0 1 1 A 0 0 0 ASSD ASSD ASSD ASSD 013 012 011 010 = = = = D0 D1 D2 D3 A S1 S0
- 36. DeMux Operations w/Enable En S1 S0 D3 D2 D1 D0 0 X X 0 0 0 0 1 0 0 0 0 0 A 1 0 1 0 0 A 0 1 1 0 0 A 0 0 1 1 1 A 0 0 0 D0 D1 D2 D3 A S1 S0 En