This document provides an introduction to basic MATLAB commands and operations. It discusses how to enter and exit MATLAB, lists some common commands like clearing the screen and workspace. It also covers defining different variable types like scalars, vectors, matrices, and character arrays. It provides examples of arithmetic operations on arrays and defines matrices. Exercises are included to practice these concepts.

1. Matlab Basic

2. MATLAB Product Family
2

3. 3

4. Entering & Quitting MATLAB
• To enter MATLAB double click on the MATLAB icon.
• To Leave MATLAB Simply type quit and press enter.
4

5. Some Basic Commands
• To check the list of installed toolboxes type
• To clear the screen type
• To move the cursor to upper left corner of the command window type
5

6. Some Basic Commands (contd…)
• To list the current variables type
• To list the current variables in long form type
• To clear the workspace type
• To remove particular variable from the workspace type
6

7. Some Basic Commands (contd…)
• To get list of Help topics type
• To get help for any topic type
• To get help for any command type
7

8. Some Basic Commands (contd…)
• To search command type
• To list the files in a directory type
• To list the Matlab files only type
8

9. 9

10. Types of MATLAB Variables
• Scalar
array
• Vector
(column vector) or (row vector)
• Matrix
• Character Arrays (Strings)
10

11. Defining Scalars
Variables are assigned numerical values by
typing the expression directly, for example,
typing
yields:
11

12. Variable Definitions
We can also assign numerical values to the variables
by typing the expression
yields:
12

13. Variable Definitions
• After typing the expressions the answers are
echoed back.
• To suppress the echo put semicolon at the end
of the expression.
13

14. Arithmetic Operators on Scalars
14
• MATLAB utilizes the following arithmetic operators:

15. Variable Definition (Contd…….)
A variable can be assigned using a formula. For example,
since a was defined previously, the following expression is
valid
yields:
15

16. Variables in Workspace
• Type who to check the stored variables in workspace.
16

17. Variables in Workspace
• Type whos to check the stored variables in long form.
17

18. Complex numbers
• A complex number 3+2i in Matlab is entered in the
following form
18

19. Complex numbers
• An exponential number 3x10-2 in Matlab is entered in the
following form
19

20. Exercise#1
Investigate the effect of following commands
20

21. Defining Vectors
• Row Vectors
• Column Vectors
21
 naaaA ...21



















nb
b
b
B
.
.
.
2
1

22. Defining Row Vectors
22
To create a row vector A simply type in:
A = [2 0 1 4 7 1 5 6 4]
1 2 3 4 5 6 7 8 9
A(5)A(2)

23. Defining Row Vectors
23
v = [2 0 1 4 7 1 5 6 4]
1 2 3 4 5 6 7 8 9
A(6:9)A(1:4)

24. Defining Column Vectors
24
To create a column vector B simply type in:
B = [3; 5; 0; 0; 1; 4; 9; -1; 1]
1
-1
9
4
1
0
0
5
3 1
2
3
4
5
6
7
8
9
B = 9x1 vector
B(5)
B(3)

25. Defining Column Vectors
25
B = [3; 5; 0; 0; 1; 4; 9; -1; 1]
1
-1
9
4
1
0
0
5
3 1
2
3
4
5
6
7
8
9
9x1 vector
B(7:9)
B(2:5)
B =

26. Arithmetic Operators (Arrays)
26

27. Exercise#2
27
Investigate the effect of the following commands:
V=[2 4 7 5] and w=[1 3 8 9]

28. Exercise#3
28
Investigate the effect of the following commands.
z=[1; 1; 0; 0]

29. Defining Matrices
29
A Matrix is a mxn array



















mnmm
n
n
aaa
aaa
aaa
M
...
.
.
.
.
.
.
.
.
.
.
.
.
...
...
21
22221
11211

30. Defining Matrices
30
To enter the matrix







43
21
M
The most obvious ways are to type
or

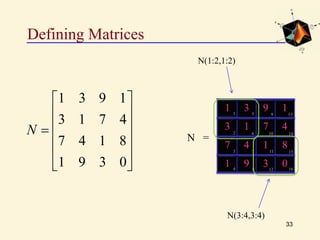
31. Defining Matrices
31













0391
8147
4713
1931
N
1 3
3 1
9 1
7 4
7 4
1 9
1 8
3 0
1
2
3
4
5
8
9
6
7
10
11
12
14
15
16
13
N =
N(1,3) or N(9)
N(4,3) or N(12)
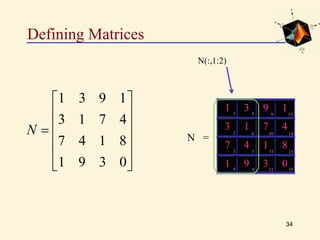
N=[1 3 9 1; 2 1 7 4; 7 4 1 8; 1 9 3 0]

32. Defining Matrices
32













0391
8147
4713
1931
N
1 3
3 1
9 1
7 4
7 4
1 9
1 8
3 0
1
2
3
4
5
8
9
6
7
10
11
12
14
15
16
13
N =
N(1:4)
N(10:12)
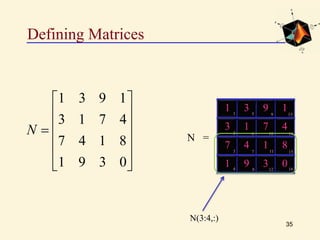
N=[1 3 9 1; 2 1 7 4; 7 4 1 8; 1 9 3 0]

33. Defining Matrices
33













0391
8147
4713
1931
N
1 3
3 1
9 1
7 4
7 4
1 9
1 8
3 0
1
2
3
4
5
8
9
6
7
10
11
12
14
15
16
13
N =
N(1:2,1:2)
N(3:4,3:4)

34. Defining Matrices
34













0391
8147
4713
1931
N
1 3
3 1
9 1
7 4
7 4
1 9
1 8
3 0
1
2
3
4
5
8
9
6
7
10
11
12
14
15
16
13
N =
N(:,1:2)

35. Defining Matrices
35













0391
8147
4713
1931
N
1 3
3 1
9 1
7 4
7 4
1 9
1 8
3 0
1
2
3
4
5
8
9
6
7
10
11
12
14
15
16
13
N =
N(3:4,:)

36. Exercise#4
36
Investigate the effect of the following commands:
M=[1 2; 3 4] N=[-1 3; 5 2]

37. Exercise#5
37
Investigate the effect of the following commands:







43
21
MM=[1 2; 3 4]

38. Exercise#6
1) Define a matrix A of dimension 2 x 4 whose (i,j) entry is A(i,j)=i+j
2) Extract two 2 x 2 matrices A1 and A2 out of the matrix A. A1 contains the
first two columns of A, A2 contains the last two columns of A
3) Compute the matrix B to be the sum of A1 and A2
4) Compute the eigen values and eigen vectors of B
5) Compute the determinant of B
6) Compute the inverse of B
7) Compute the rank of B

39. Defining Character Arrays (Strings)
39
Character arrays are created using single quote delimiter
1 2 3 4 5 6

40. Defining Character Arrays (Strings)
40
1 2 3 4 5 6

41. Conversion B/W Numeric & String Arrays
• To convert from numeric to string array
– num2str
• To convert from string array to numeric array
– str2num
41

42. Numeric to string conversion
42

43. String to Numeric conversion
43

44. QUESTIONS
Thank you for your concentration
44