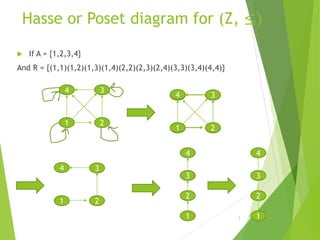
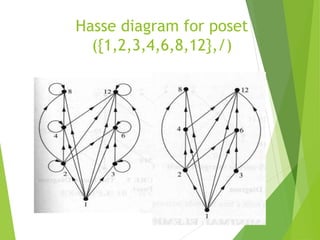
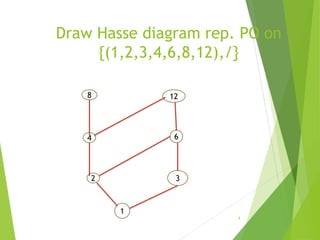
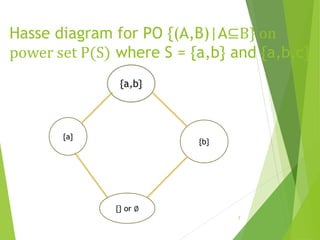
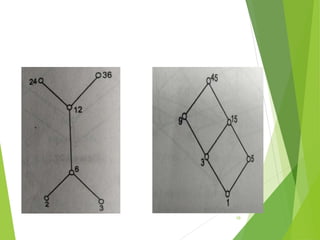
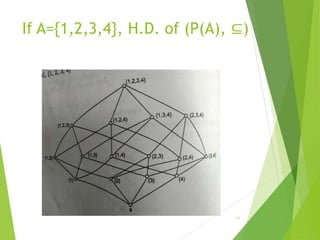
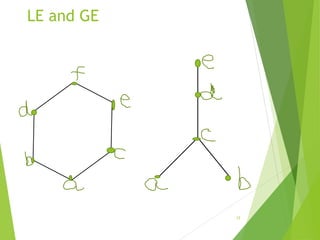
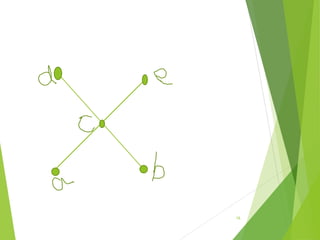
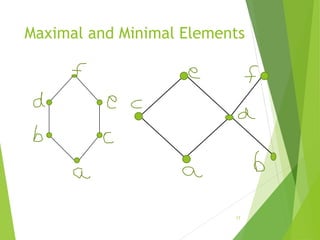
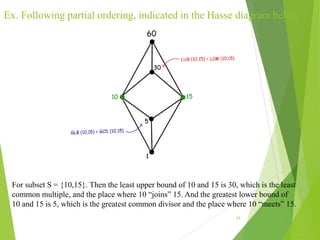
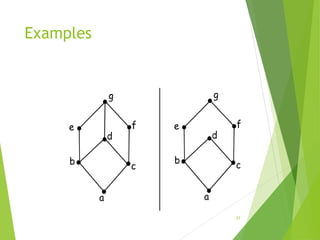
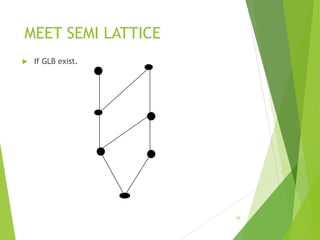
This document discusses lattices and partial orders. It defines a partial order as a relation that is reflexive, antisymmetric, and transitive. A lattice is a partially ordered set where every two elements have a unique least upper bound (join) and greatest lower bound (meet). The document provides examples of partial orders and discusses various types of lattices including bounded, complemented, distributive, and Boolean lattices. It also discusses concepts like sublattices, chains, extremal elements, and diagrams used to represent partial orders like Hasse diagrams.

1. Lattice
1

2. Partial Ordering Relation(POSET)
 A Relation R on a set A is said to be partial order relation if it is :-
Reflexive, AntiSymmetric and Transitive.
If A = {1,2,3}
 R1 = { }…No
 R2 = {(1,1),(2,2), (3,3)}……Yes
 R3 = {(1,1),(2,2), (3,3), (1,2) (2,1)}….No
 R4 = {(1,1),(2,2), (3,3), (1,3) (2,3)}…Yes
 R5 = {(1,1),(2,2), (1,2) (1,3) (2,1) (3,1)} ……No
 R6 = {(1,1),(2,2), (3,3), (1,2) (2, 3)}….No
 R7 = A X A ….No 2

3. Hasse or Poset diagram for (Z, ≤)
 If A = {1,2,3,4}
And R = {(1,1)(1,2)(1,3)(1,4)(2,2)(2,3)(2,4)(3,3)(3,4)(4,4)}
3
1 2
3
4
1 2
3
4
4
1 2
3
4
1 2
3
4
4
3
2
1
4
3
2
1

4. POSET (A,R)
 Partial Order Relation with Set.
 For ex.
 1. {(1,2,3,4,5), ≤ }
 2. {(1,2,3,4,6,12), /}
 3. {(1,2,3,5,6,10,15,30), /}
4

5. Hasse diagram for poset
({1,2,3,4,6,8,12},/)
5

6. Draw Hasse diagram rep. PO on
{(1,2,3,4,6,8,12),/}
6
8 12
4
1
2
6
3

7. Hasse diagram for PO {(A,B)|A⊆B} on
power set P(S) where S = {a,b} and {a,b,c}
7
{a}
{b}
{} or ∅

8. P(S)= 8 el
({},{a},{b},{c},{a,b},{b,c},{a,c},{a,b,c})
8

9. Examples for Practice
 Let X = {2, 3, 6, 12, 24, 36} then prove (X, /) is a poset and
draw its Hasse diagram.
 Draw the Hasse diagram of Poset (D45, /), where D45 = {1, 3,
5, 9, 15, 45}
 IF A = {1, 2, 3, 4}. Draw Hasse Diagram of (P(A), ⊆)
9

10. 10

11. If A={1,2,3,4}, H.D. of (P(A), ⊆)
11

12. Defination of LB, GLB, UB, LUB
 Let (P,≤)be a poset, and A ≤ P, then a ∈ A is called a lower bound(LB) of
A if a≤ x, ∀x ∈ A.
 If there are no lower bounds of A which are greater than a, then a is
called greatest lower bound (GLB) of A or Infimum of A.
 Let (P,≤)be a poset, and A ≤ P, then a ∈ A is called a upper bound (UB) of
A if a ≥ x, ∀x ∈ A.
 If there are no upper bounds of A which are less than a, then a is called
least upper bound (LUB) of A or supremum of A.
12

13. D24={1,2,3,4,6,8,12,24}, relation
divides. Find LB and GLB, UB and LUB.
 Find LB of {8,12}
 Find GLB of {8, 12}
 Find UB of {8, 12}
 Find LUB of {8,12}
13

14. Special Elements in Posets
 Let (P, ≤) be a Poset, and A ⊆ P, then
(i) an element a ∈ A is called Least Element (LE) of A if a ≤ x, ∀x ∈ A.
(ii) an element a ∈ A is called the Greatest Element (GE) of A if a ≥ x, ∀x ∈ A.
Note:-
1. If Least Element of A exists then it is Unique.
2. If Greatest Element of A exists then it is Unique.
14

15. LE and GE
15

16. 16

17. Maximal and Minimal Elements
17

18. NOTE:--
 1. Minimal or Maximal Element is not Unique.
 2. Least Element of A is Minimal Element, but not converse.
 3. Greatest Element of A is Maximal Element, but converse
need not be true.
18

19. Lattice
 A lattice is an abstract structure studied in the
mathematical subdisciplines of order theory and
abstract algebra. It consists of a partially ordered set in
which every two elements have a unique supremum
(also called a least upper bound or join) and a unique
infimum (also called a greatest lower bound or meet).
19

20.  Formally, a lattice is a poset, a partially ordered
set, in which every pair of elements has both a
least upper bound (LUB) and a greatest lower
bound (GLB). In other words, it is a structure
with two binary operations:
 LUB/Join ( ⋁ )
 GLB/Meet ( ⋀ )
20

21. Recap
 So to understand lattices and their structure, we need to take a step
back and make sure we understand the extremal elements of a poset
because they are critical in understanding lattices.
 Recall, a relation R is called a partial ordering, or poset, if it is
reflexive, antisymmetric, and transitive, and the maximal and
minimal elements in a poset are quickly found in a Hasse diagram
as they are the highest and lowest elements respectively.
21

22.  Note that the LUB of a pair of two elements is the
same as finding the least common multiple (LCM),
and the GLB of a pair of two elements is the same as
finding the greatest common divisor (GCD)
22

23. Table below denotes the LUB and GLB in terms of the join
and meet and some alternate notation for each.
23

24. Ex. Following partial ordering, indicated in the Hasse diagram below
24
For subset S = {10,15}. Then the least upper bound of 10 and 15 is 30, which is the least
common multiple, and the place where 10 “joins” 15. And the greatest lower bound of
10 and 15 is 5, which is the greatest common divisor and the place where 10 “meets” 15.

25. Examples
25

26.  The partial ordering on the left indicates a lattice because
each pair of elements has both a least upper bound
(LUB) and greatest lower bound (GLB). In other words,
each pair of elements is comparable.
 However, the partial ordering on the right is not a lattice
because elements b and c are incomparable. Notice that
while the upper bound for b and c is {d, e, f, g}, we can’t
identify which one of these vertices is the least upper
bound (LUB) — therefore, this poset is not a lattice.
26

27. Several Types of Lattices
 Semi Lattices :-- Join Semi Lattice - If LUB exist and Meet Semi
Lattice – If GLB exist.
 SubLattice :-- If (L,R) be lattice then (M,R) is a Sublattice of (L,R) if
M⊆L.
 Complete Lattice – all subsets of a poset have a join and meet, such as
the divisibility relation for the natural numbers or the power set with the
subset relation.
 Bounded Lattice – if the lattice has a least and greatest element,
denoted 0 and 1 respectively.
 Complemented Lattice – a bounded lattice in which every element is
complemented. Namely, the complement of 1 is 0, and the complement.
 Distributive Lattice- A lattice L is called distributive lattice if for any
elements a, b and c of L, it satisfies distributive properties.
 Boolean Lattice- If both CL and DL satisfies, then it is BL. It means
exactly one complement . 27

28. JOIN SEMI LATTICE
 If LUB exist.
28

29. MEET SEMI LATTICE
 If GLB exist.
29

30. SubLattice
 If (L,R) be lattice then (M,R) is a Sublattice of (L,R) if M⊆L.
 a, b ∈ M  (a ⋁ b) and (a ⋀ b) ∈ M
30

31. Bounded Lattices
 A lattice L is called a bounded lattice if it has greatest element 1 and a
least element 0.
 Example:
1. The power set P(S) of the set S under the operations of intersection and
union is a bounded lattice since ∅ is the least element of P(S) and the set
S is the greatest element of P(S).
2. The set of +ve integer I+ under the usual order of ≤ is not a bounded lattice
since it has a least element 1 but the greatest element does not exist.
 (Z,≤) GE, LE does not exist.
 LUB(a,b) = Max (a,b)
 GLB(a,b) = Min (a,b)
31

32.  Thus, the greatest element of Lattices L is a1∨ a2∨ a3∨....∨an.
 Also, the least element of lattice L is a1∧ a2∧a3∧....∧an.
 Since, the greatest and least elements exist for every finite lattice. Hence,
L is bounded.
32

33. Complement Lattice
 In a Bounded Lattice (L,R) which has GE=1 and LE=0, an
element b ∈ L is called Complement of an element a ∈ L if a⋁ b
= 1 and a ⋀ b =0.
 LUB = JOIN = a⋁ b = GE = 1
 GLB = MEET = a ⋀ b =LE=0
33

34. 34

35. Distributive Lattice
 Let L be a non-empty set closed under two binary operations called meet and
join, denoted by ∧ and ∨. Then L is called a lattice if the following axioms hold
where a, b, c are elements in L:
1) Commutative Law: -
(a) a ∧ b = b ∧ a (b) a ∨ b = b ∨ a
2) Associative Law:-
(a) (a ∧ b)∧ c = a ∧(b∧ c) (b) (a ∨ b) ∨ c = a ∨ (b ∨ c)
3) Absorption Law: -
(a) a ∧ ( a ∨ b) = a (b) a ∨ ( a ∧ b) = a
4) Distributive Property :- May or may not be satisfied by a lattice.
35

36. Defination…
 Distributive lattice is a lattice in which the operations of join and
meet distribute over each other. The prototypical examples of such
structures are collections of sets for which the lattice operations can be
given by set union and intersection. A lattice L is called distributive lattice if for
any elements a, b and c of L, it satisfies following distributive properties:
 a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)
 a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)
 If the lattice L does not satisfies the above properties, it is called a non-distributive
lattice.
Duality:
 The dual of any statement in a lattice (L,∧ ,∨ ) is defined to be a statement that is
obtained by interchanging ∧ an ∨.
36

37. 37

38.  In DL complement of all elements have at most 1, So in DL if an
element has a complement then it is unique.
 If 2 or more complement exists then it is not DL.
38

39. For ( Dn, /) set of positive divisor of n, belongs to N,
and relation is divide, Find Dn for some n, draw Hasse
diagram whether it is chain or not, Also find condition
of chain lattice...
 (D4,/)
 (D10,/)
 (D27,/)
 (D28,/)
 (D32,/)
 (D36,/)
 (D48,/)
 (D125,/)
 (D49,/)
 (D50,/)
39

40. 40

41. Boolean Lattice
 A Boolean lattice is defined as any lattice that is complemented
and distributive. In any Boolean lattice , the complement of each
element is unique.
 A Boolean lattice is a complemented distributive lattice. Thus, in a
Boolean lattice B, every element a has a unique complement,
and B is also relatively complemented.
 If both CL and DL satisfies, then it is BL. It means exactly one
complement .
 For ex. (D10, /), (D15, /)
41

42. 42

43. References
1. Liptschutz, Seymour, “ Discrete Mathematics”, McGraw Hill. 3rd edition.
2. Trembley, J.P & R. Manohar, “Discrete Mathematical Structure with
Application to Computer Science”, McGraw Hill, Reprint 2010
3. Discrete Mathematics & its application with combinatory and graph
theory, K.H.Rosen, TMH (6th ed).
4. C.L.Liu, „Discrete Mathematics‟ TMH.
5. https://www.tutorialspoint.com › discrete_mathematics
6. https://www.geeksforgeeks.org › relations-and-their-types
7. https://nptel.ac.in ›

43

44. THANK YOU
44