This document provides an overview of MATLAB, including the MATLAB desktop, variables, vectors, matrices, matrix operations, array operations, built-in functions, data visualization, flow control using if and for statements, and user-defined functions. It introduces key MATLAB concepts like the command window, workspace, and editor. It also demonstrates how to create and manipulate variables, vectors, matrices, and plots in MATLAB.

1. Outline
• What is MATLAB
• MATLAB desktop
• Variables, Vectors and Matrices
• Matrix operations
• Array operations
• Built-in functions: Scalar, Vector, Matrix
• Data visualization− 2D Plots
• Flow control: ‘if’, ‘for’
• User-defined functions
1

2. • High level language for technical
computing
• Stands for Matrix Laboratory
• Easy to do linear algebra, calculus,
signals and systems and the most
complex calculations a human brain
can think of.
What is MATLAB
MATLAB
High level languages,
C, C++, Basic,
Fortran, Pascal, etc.
Assembly
Language
2

3. MATLAB desktop
3

4. MATLAB desktop (cont.)
1. Menu and toolbar
2. Command window
4

5. MATLAB desktop (cont.)
3. Command history 4. Workspace
5

6. MATLAB desktop (cont.)
5. Variable editor
6

7. MATLAB desktop (cont.)
6. Editor
7

8. MATLAB basics
What is difference?
Variable Vector/Array Matrix
1×1
Single value
1×N or M×1
Row or column vector
M×N
𝑎 = 5 𝑦 = 2 3 7
or
𝑦 =
2
3
7
𝑧 =
1 4
7 3
8

9. Variables
• No need for types. i.e.
• All variables are created with double precision unless
specified.
• After these statements, the variables are 1×1 matrices with
double precision.
• Enter ‘who’ command in command window to view all
active variables
• Enter ‘whos’ command to view all active variables with
their size, allocated memory size and type of variable.
int a;
double b;
float c;
Example:
>> a = 5;
>> b = 2;
9

10. Vectors
• Vector in space
𝑍 = 2 𝑎 𝑥 + 3 𝑎 𝑦 + 7 𝑎 𝑧
• Can be written as
• Use ‘space’ (‘ ’) or ‘comma’ (‘,’) to separate row elements.
• Use ‘semicolon’ (‘;’) to separate rows.
• Define a row vector ‘r’ and column vector ‘c’.
• If we no longer need a particular variable/vector/
/matrix/object we can “erase” it from memory using the
command ‘clear variable_name’.
• Erase vector ‘r’.
2 3 7
or
2
3
7
Row vector Column vector
>> r = [1 2 3 4 5]; or r = [1,2,3,4,5];
>> c = [6;7;8;9;10];
10

11. Matrices
• Almost all entities in MATLAB are matrices.
• Order of Matrix − m × n
m = number of rows
n = number of rows
• Vectors are special case of Matrices
− m = 1 row vector
− n = 1 column vector
• Define
• A vector is always a matrix but a matrix is not necessarily a
vector
• Use ‘size (variable/vector/matrix name)’ to find its size.
>> A = [1 2; 3 4]
>> B = [16 3 5; 7 5 10]
11

12. Creating Vectors
• Creating vector with equally spaced intervals
>> x = 0:0.5:2
x =
0 0.5000 1.0000 1.5000 2.0000
• Creating vector with n equally spaced intervals
>> x = linspace(0,2,5)
x =
0 0.5000 1.0000 1.5000 2.0000
12

13. Creating Matrices from functions
• zeros(m, n): matrix with all zeros
• ones(m, n): matrix with all ones.
• eye(m, n): the identity matrix
• rand(m, n): uniformly distributed random
• randn(m, n): normally distributed random
• magic(m): square matrix whose elements have the
same sum, along the row, column and diagonal.
13

14. Matrix operations
• ^: exponentiation
• *: multiplication
• /: division
• : left division. The operation AB is effectively the
same as INV(A)*B, although left division is
calculated differently and is much quicker.
• +: addition
• -: subtraction
14

15. Array operations
• Evaluated element by element
• .’ : array transpose
• .^ : array power
• .* : array multiplication
• ./ : array division
• Very different from Matrix operations
15

16. Example
Perform the following task.
• Define matrices ‘A’ and ‘B’
>> A=[1 2;3 4];
>> B=[5 6;7 8];
Find product of ‘A’ and ‘B’ using Matrix and Array
operator.
Which one is correct??
Hint: Solve on paper before using MATLAB
16

17. Matrix Indexing
Given the matrix:
Then:
A(1,2) = 0.6068
A(3) = 0.6068
A(:,1) = [0.9501
0.2311 ]
A(1,2:3)=[0.6068 0.4231]
𝐴 =
0.9501 0.6068 0.4231
0.2311 0.4860 0.2774
17

18. Adding Elements to a Vector or a Matrix
>> C=[1 2; 3 4]
C=
1 2
3 4
>> C(3,:)=[5 6];
C=
1 2
3 4
5 6
>> D=linspace(4,12,3);
>> E=[C D’]
E=
1 2 4
3 4 8
5 6 12
>> A=1:3
A=
1 2 3
>> A(4:6)=5:2:9
A=
1 2 3 5 7 9
>> B=1:2
B=
1 2
>> B(5)=7;
B=
1 2 0 0 7
18

19. Built-in Functions: Scalar Functions
• sin: trigonometric sine
• cos: trigonometric cosine
• tan: trigonometric tangent
• asin: trigonometric inverse sine (arcsine)
• acos: trigonometric inverse cosine (arccosine)
• atan: trigonometric inverse tangent (arctangent)
• exp: exponential
• log: natural logarithm
• log10: base 10 logarithm
• abs: absolute value
• angle: phase value
• sqrt: square root
• rem: remainder 19

20. Built-in Functions: Vector Functions
• max: largest component
• min: smallest component
• length: length of a vector
• sort: sort in ascending order
• sum: sum of elements
• prod: product of elements
• mean: mean value
• std: standard deviation
20

21. Built-in Functions: Matrix Functions
• size: size of a matrix
• det: determinant of a square matrix
• inv: inverse of a matrix
• rank: rank of a matrix
• rref: reduced row echelon form
• eig: eigenvalues and eigenvectors
• poly: characteristic polynomial
• lu: LU factorization
• qr: QR factorization
• chol: cholesky decomposition
• svd: singular value decomposition
21

22. Data visualization − 2D plots
• If ‘x’ and ‘y’ are two vectors of the same length then
‘plot(x,y)’ plots x versus y.
• Example:
Plot y=cos(x) from −π to π with increment of 0.01
» x=-pi:0.01:pi;
» y=cos(x);
» plot(x,y)
22

23. 2D plots − Overlay plots
• To change curve style, specify marker style
plot(xdata, ydata, ‘marker_style’);
• Example
>> x=-5:0.1:5;
>> y=x.^2;
>> p1=plot(x, y, 'r:s');
• Use hold on for overlaying graphs
>> hold on;
>> z=x.^3;
>> p2=plot(x, z,‘b-o');
23

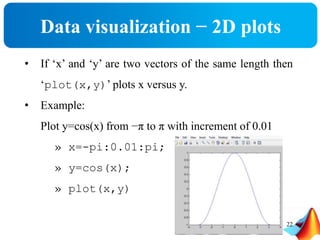
24. 2D plots − Annotation
• Use title, xlabel, ylabel and legend for
annotation
Example
>> title('Demo plot');
>> xlabel('X Axis');
>> ylabel('Y Axis');
>> legend([pl, p2], 'x^2', 'x^3');
24

25. 2D plots − Line types
• y: yellow
• m: magenta
• c: cyan
• r: red
• g: green
• b: blue
• w: white
• k: black
• .: point
• o: circle
• x: x-mark
• +: plus
• -: solid
• *: star
• :: dotted
• -.: dashdot
• --: dashed
25

26. 2D plots − Other commands
• figure: opens new window for plot
• close all: closes all opened figures
• subplot: creates an array of plots in the same
window
• loglog: plot using log-log scale
• semilogx: plot using log scale on the x-axis
• semilogy: plot using log scale on the y-axis
26

27. Flow control: ‘for’ loop
• A loop is a statement which is executed repeatedly.
• If you want to repeat some commands, you can use
‘for’ loop.
• Must tell MATLAB where to start and where to end.
for index = start : end
program statements
:
end
• Example
for i=1:4
i
end 27

28. Flow control: ‘if’ statement
• Execute statements if condition
is true
if (condition_1)
program statements
elseif (condition_2)
program statements
else
program statements
end
28
• Dummy examples
if (x<5)
:
end
if (a<3)
:
elseif (b~=5)
:
end

29. Flow control: Operators
29
• Logical operators
• <: less than
• >: greater than
• <=: less than or equal to
• >=: greater than or equal to
• ==: equal to
• ~=: not equal to
• Logical operators
• &: and
• |: or
• ~: not

30. User-defined functions
30
• Functions are m-files which can be executed by
specifying some inputs and supply some desired
outputs.
function output = functionname(inputs)
function [out1,out2,…] = functionname(in1,in2…)
• Write this command at the beginning of the m-file and save the
m-file with a file name same as the function name.

31. User-defined functions (cont.)
31
Examples
• Write a function which takes a number and returns its
square.
• Write a function which takes the square of the input matrix
if the input indicator is equal to 1. And takes the element
by element square of the input matrix if the input indicator
is equal to 2