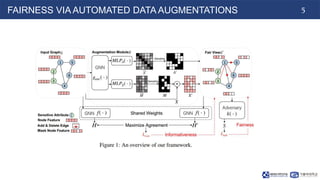
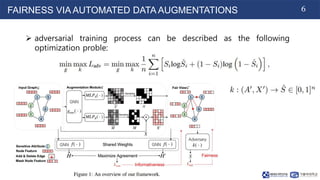
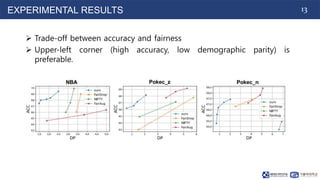
The document proposes Graphair, a method for fair graph representation learning via automated data augmentations. Graphair uses an adversarial process to automatically discover fairness-aware data augmentation strategies for different graph datasets. The augmentation process modifies graphs by perturbing edges and masking node features. Graphair aims to learn representations that achieve demographic parity and equal opportunity while preserving predictive accuracy. Experimental results on node classification tasks show Graphair achieves better fairness metrics than baselines while maintaining high accuracy.

1. Van Thuy Hoang
Dept. of Artificial Intelligence,
The Catholic University of Korea
hoangvanthuy90@gmail.com
Ling et al., ICLR 2023

2. 2
Problems
 A primary issue in fairness is that training data usually contain biases,
which is the source of discriminative behavior of models.
 many existing works propose to learn fair graph representations by
modifying training data with fairness-aware graph data
augmentations.
 However, the proposed graph properties may not be appropriate for
all graph datasets due to the diverse nature of graph data. For
example, balanced inter/intra edges may destroy topology
(Mehrabi et al., 2021; Olteanu et al., 2019)

3. 3
Problems
 it is highly desirable to automatically discover dataset-specific
fairness-aware augmentation strategies among different datasets
with a single framework. To this end, a natural question is raised:
 Can we achieve fair graph representation learning via automated
data augmentations?

4. 4
FAIR GRAPH REPRESENTATION LEARNING
 Given a graph:
 Where: is the vector containing sensitive attributes (e.g.,
gender or race) of nodes that should not be captured by machine
learning models to make decisions.
 target is to learn a fair graph representation model
focus on group fairness, which is defined as:

5. 5
FAIRNESS VIA AUTOMATED DATA AUGMENTATIONS

6. 6
FAIRNESS VIA AUTOMATED DATA AUGMENTATIONS
 adversarial training process can be described as the following
optimization proble:

7. 7
FAIRNESS VIA AUTOMATED DATA AUGMENTATIONS
 Augmentation process:
 TA is the edge perturbation transformation, which maps A to the
new adjacency matrix A′ by removing existing edges and adding new
edges. TX is the node feature masking transformation, which
produces the new node feature matrix X′ by setting some values of X
to zero.

8. 8
FAIRNESS VIA AUTOMATED DATA AUGMENTATIONS
 Edge perturbation.
 Node feature masking:

9. 9
Loss function
 contrastive objective for any positive pair
 L_BCE and L_MSE denote binary cross-entropy loss and mean
squared error loss:

10. 10
Loss function
 The overall training process can be described as the following min-
max optimization procedure

11. 11
EXPERIMENTS
 Metrics:
 demographic parity
 equal opportunity
 where Y and Yˆ denote ground-truth labels and predictions,
respectively. Note that a model with lower DP and EO implies
better fairness performance

12. 12
EXPERIMENTAL RESULTS
 Comparisons between our method and baselines on node
classification tasks

13. 13
EXPERIMENTAL RESULTS
 Trade-off between accuracy and fairness
 Upper-left corner (high accuracy, low demographic parity) is
preferable.

14. 14
CONCLUSIONS
 Graphair, an automated graph augmentation method for fair
representation learning.
 Graphair uses an automated augmentation model to generate new
graphs with fair topology structures and node features, while
preserving the most informative components from input graphs.
 Adversarial learning and contrastive learning to achieve fairness and
informativeness simultaneously in the augmented data