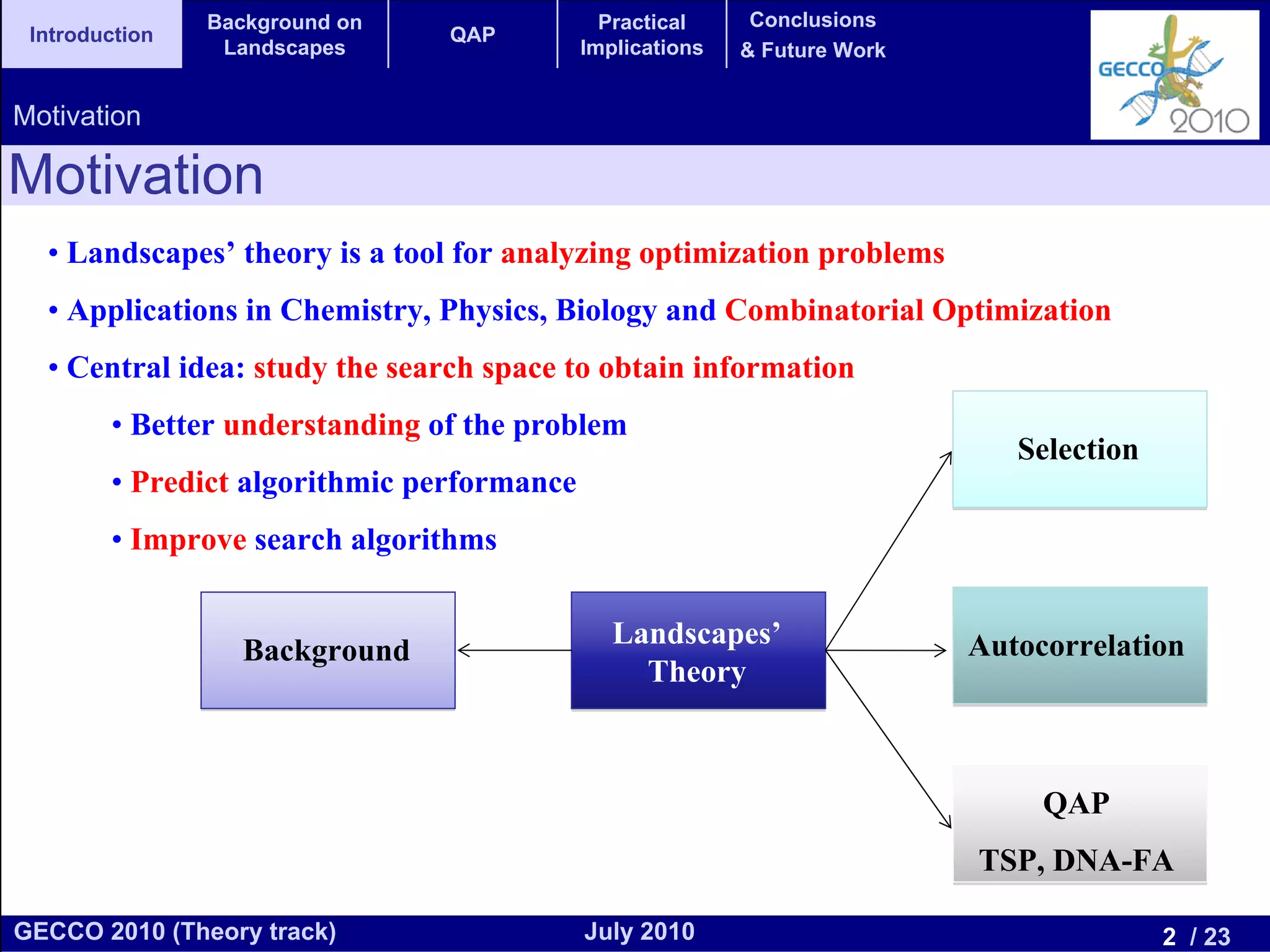
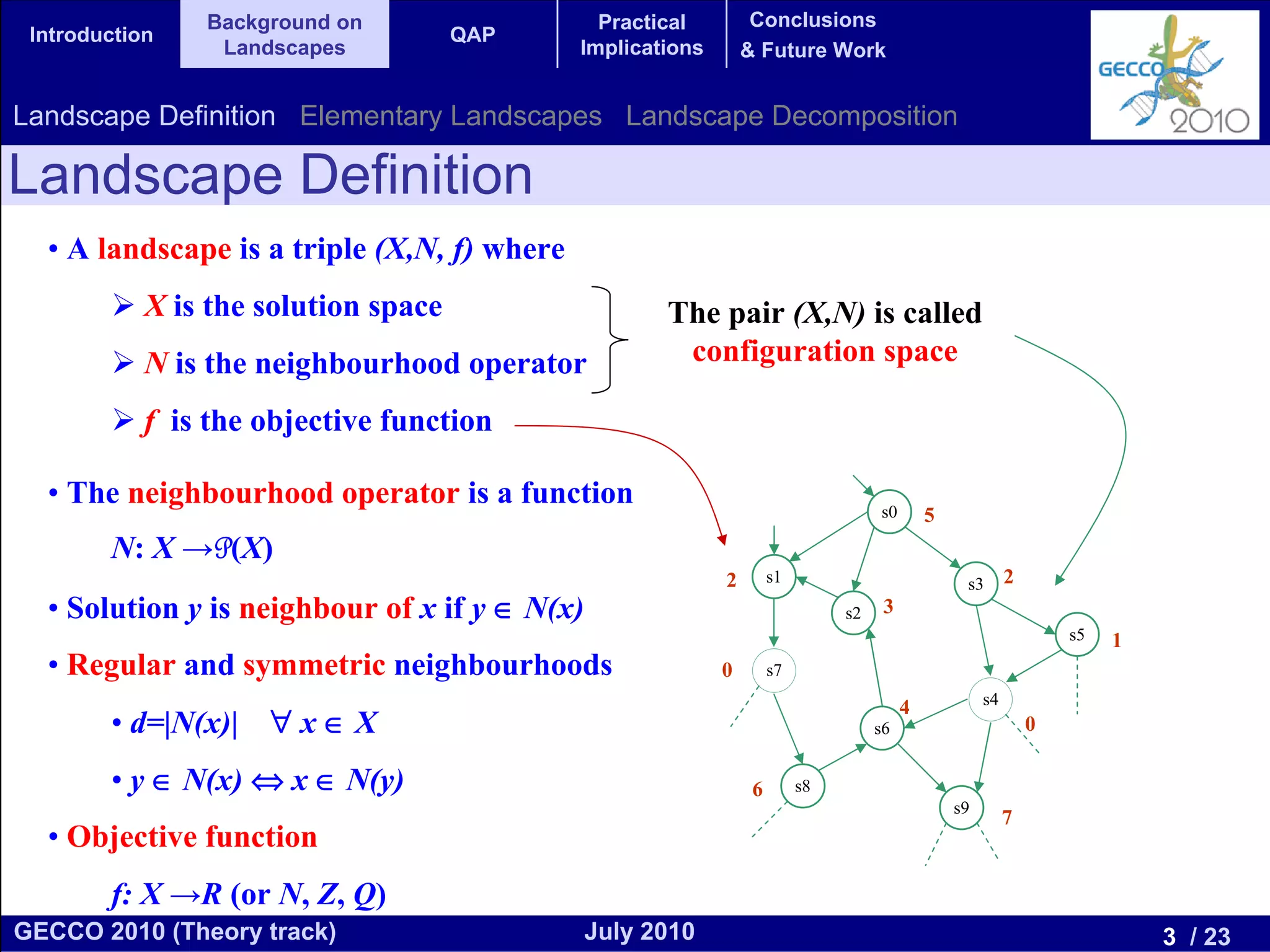
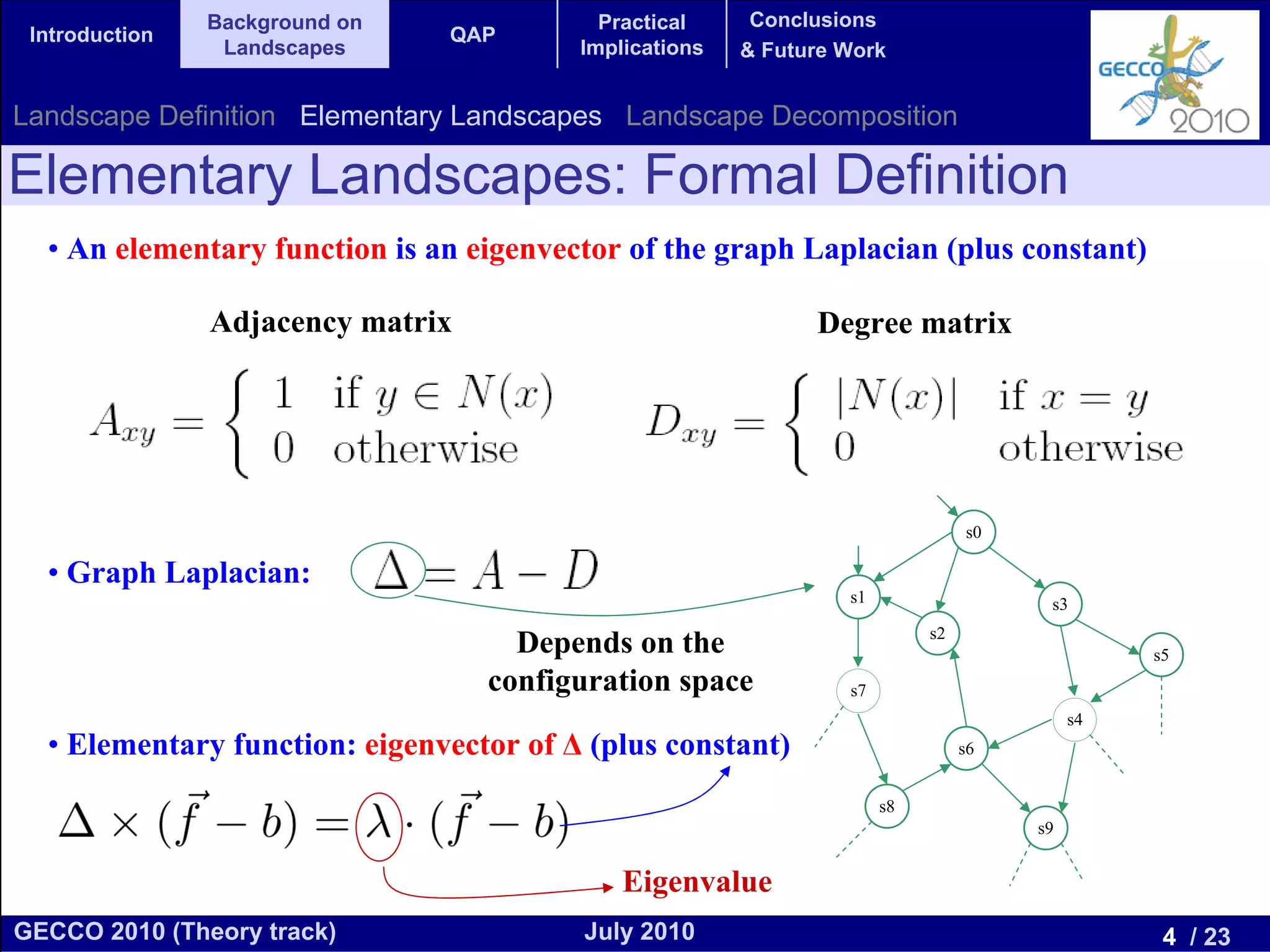
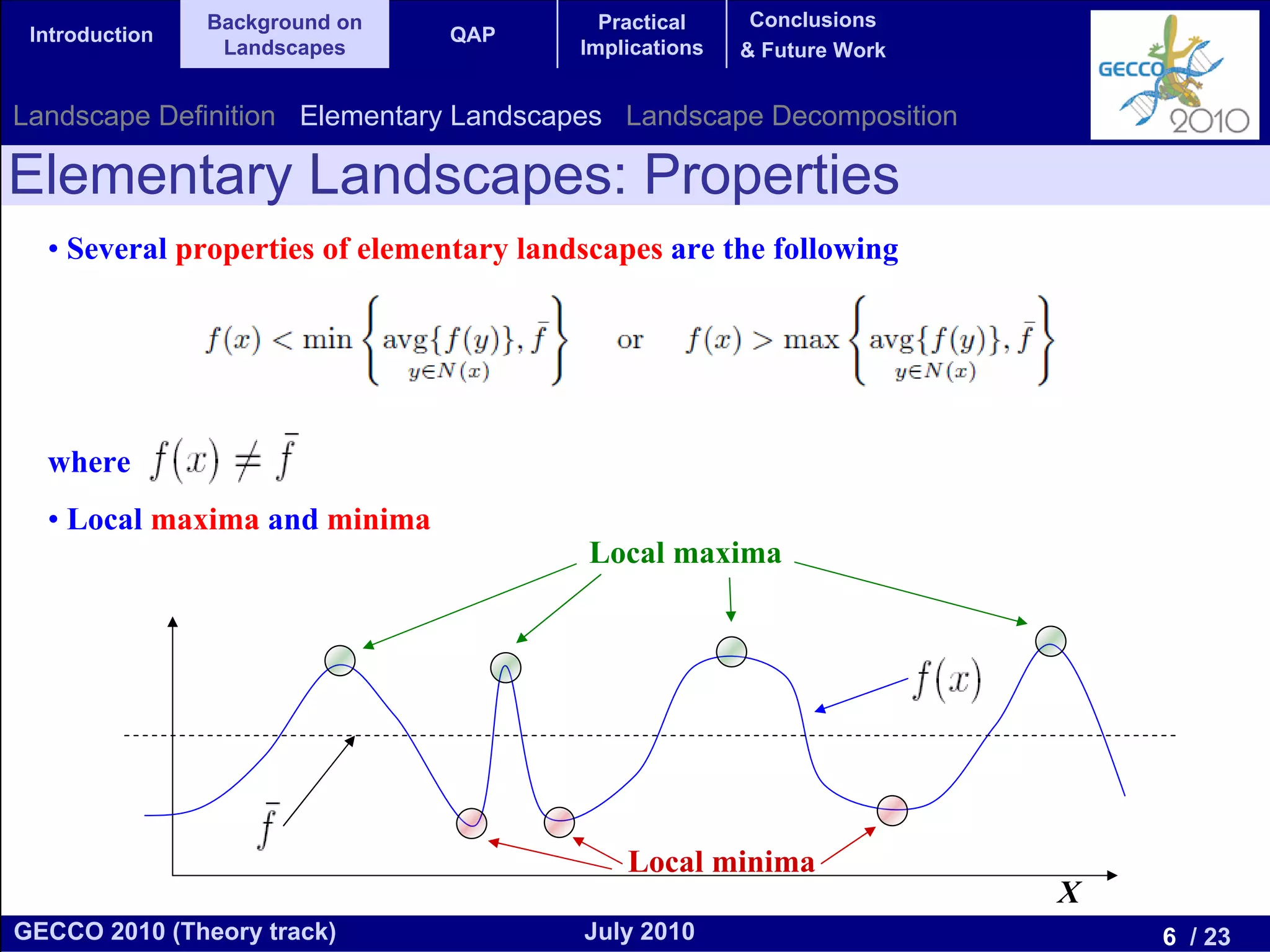
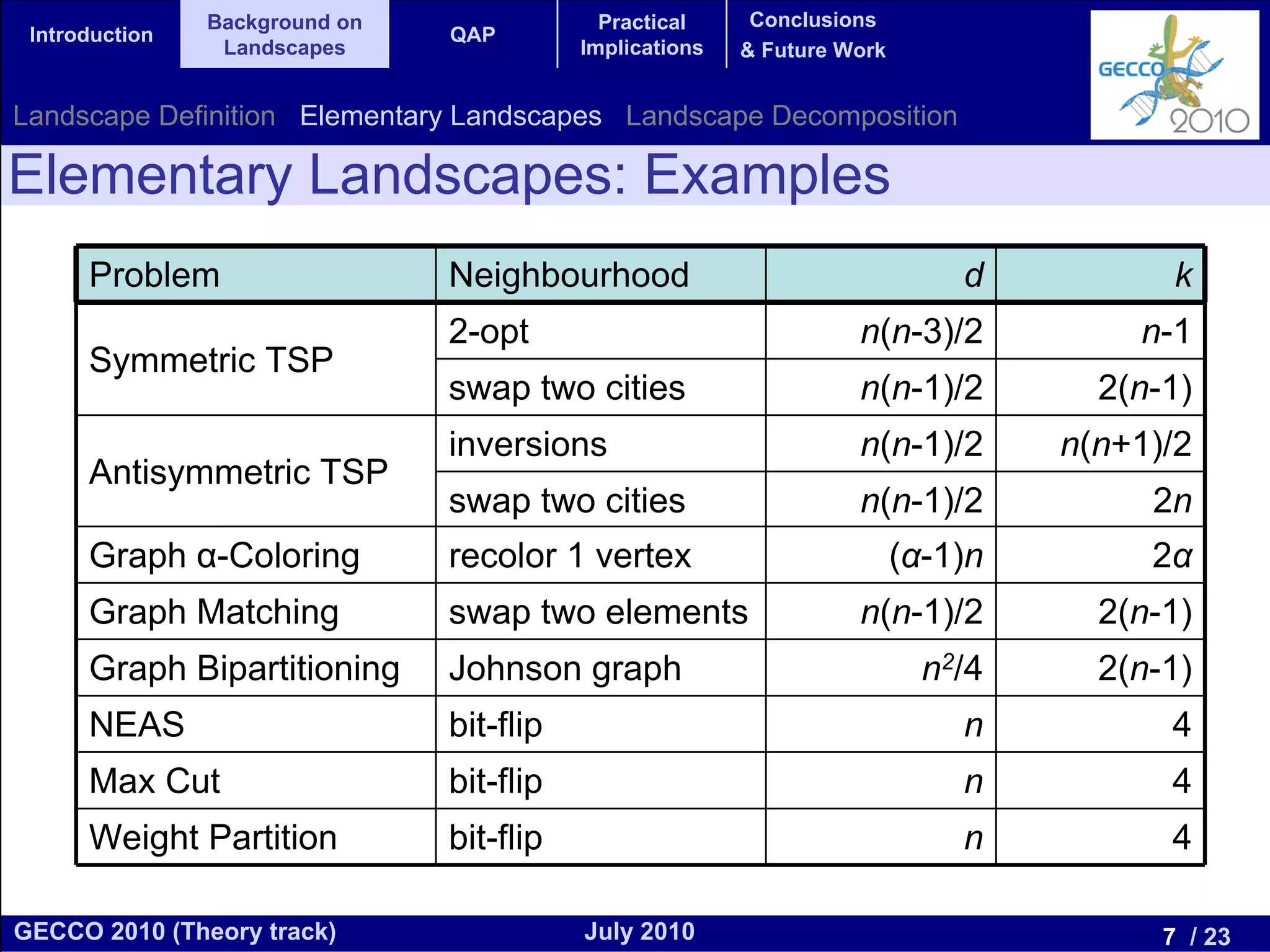
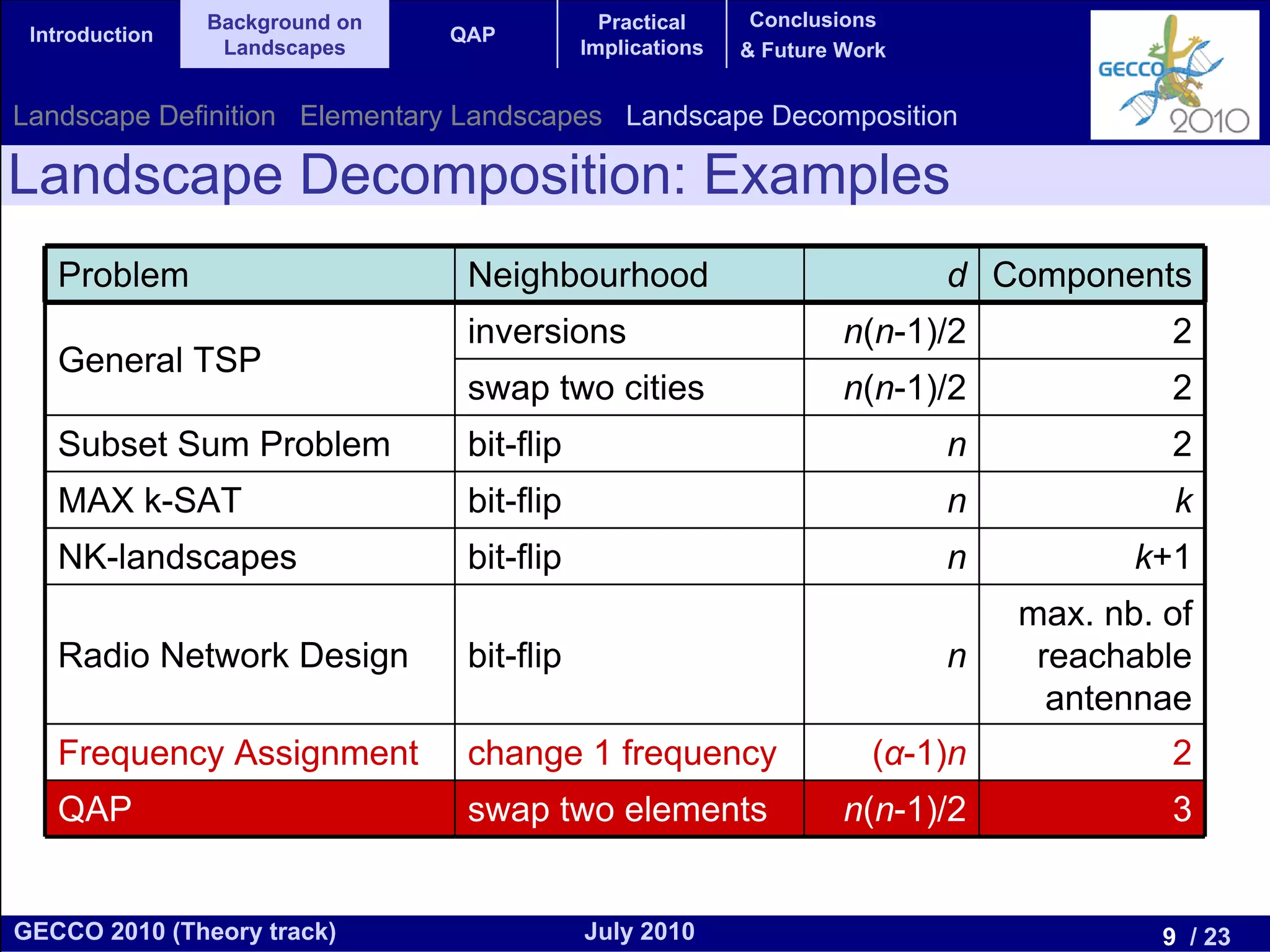
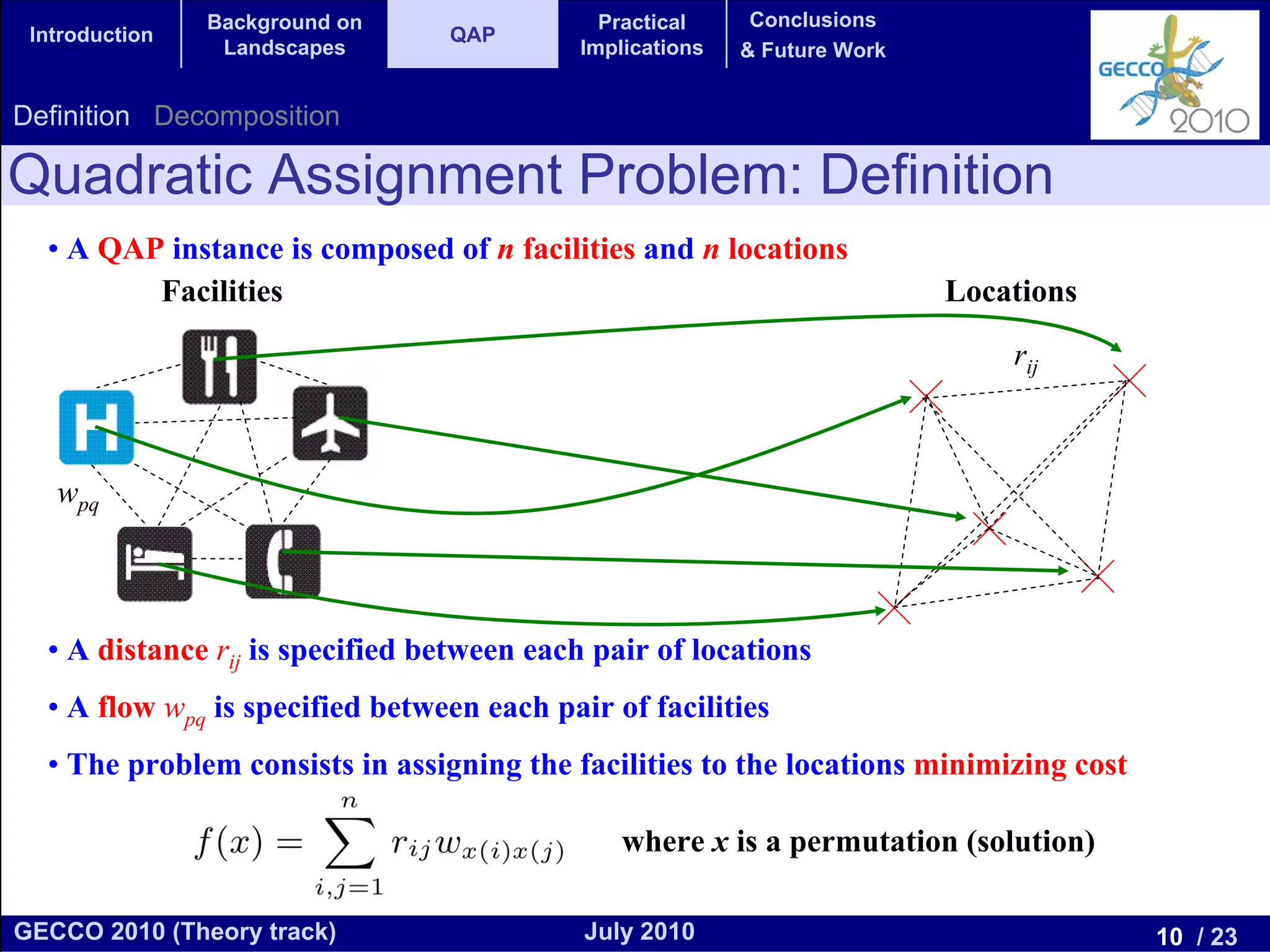
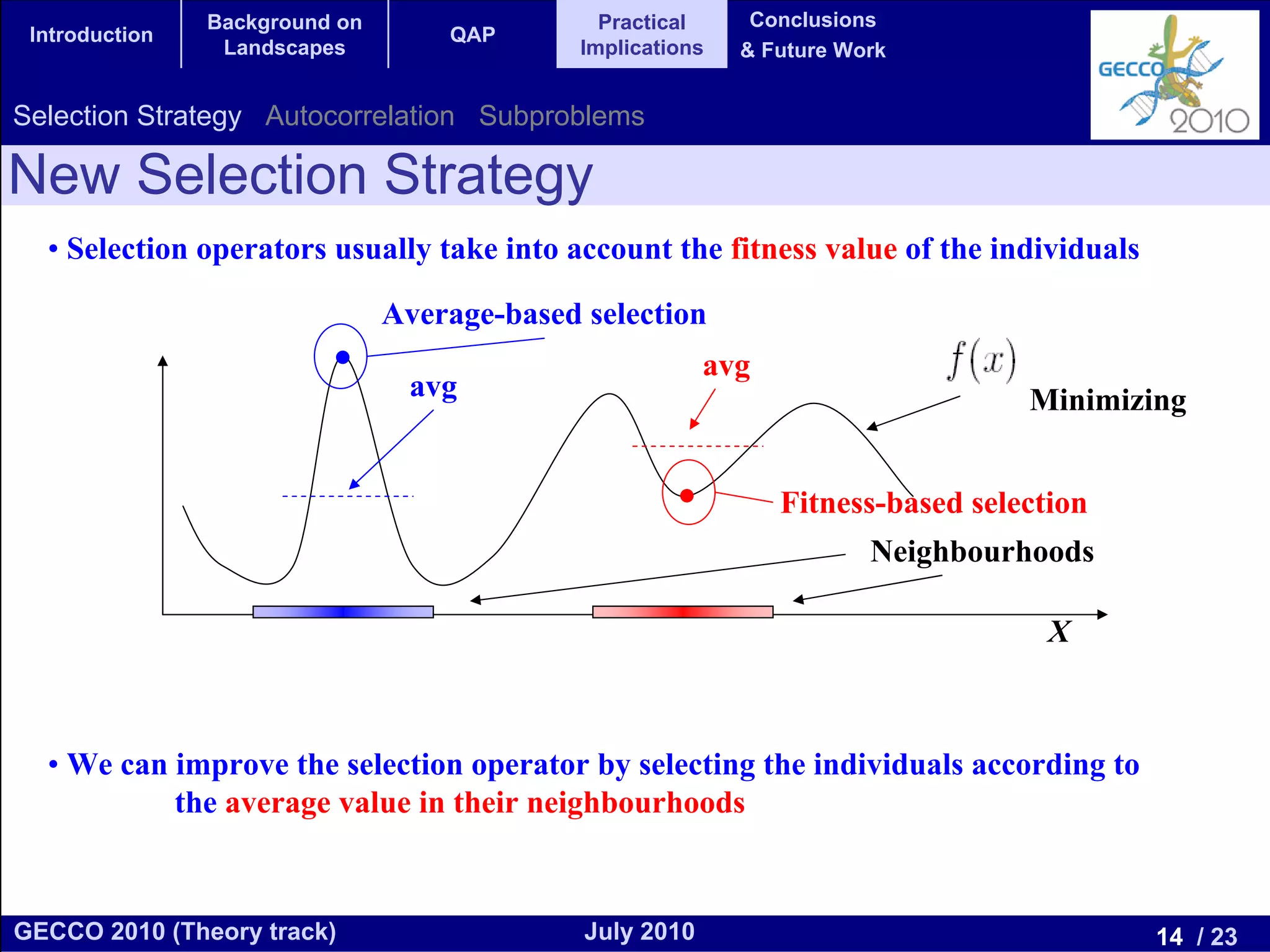
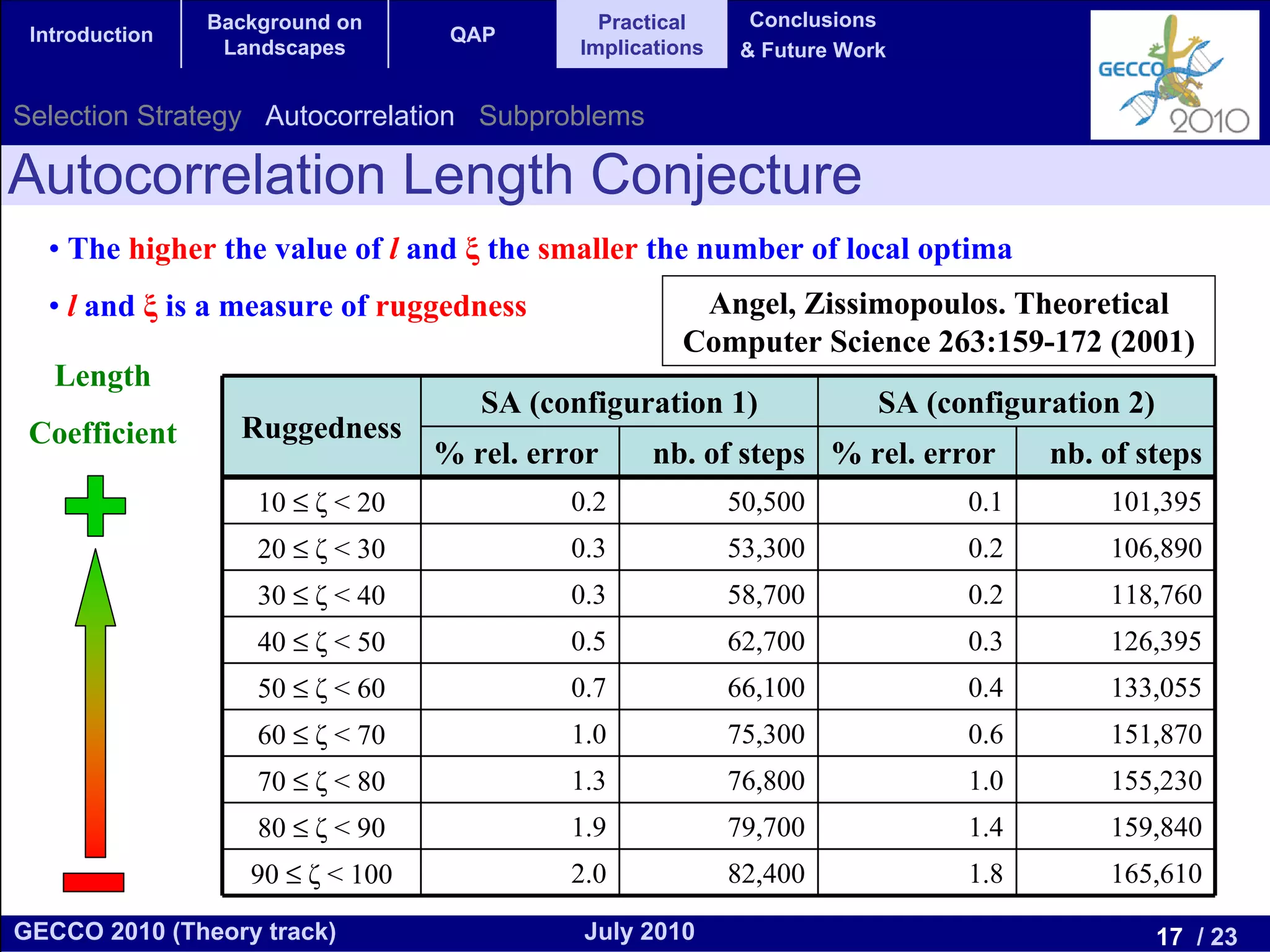
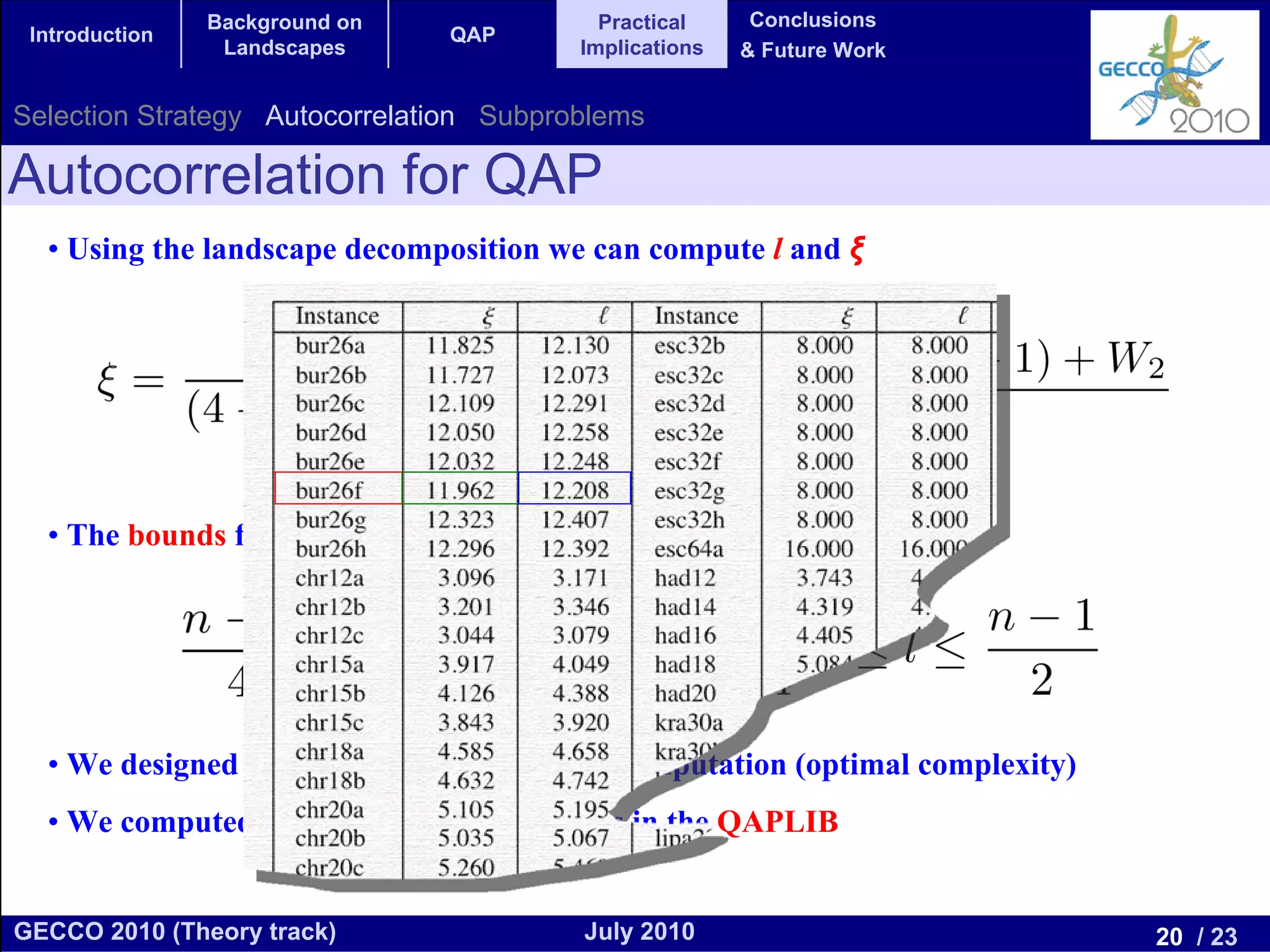
This document discusses the elementary landscape decomposition of the Quadratic Assignment Problem (QAP). It begins with background on landscape theory and definitions. It then shows that the QAP fitness function can be decomposed into three elementary components. It discusses how this decomposition allows estimating autocorrelation parameters to analyze problem structure. Finally, it notes the decomposition provides insights and can inform algorithm design, and discusses applications to related problems like the Traveling Salesman Problem and DNA fragment assembly.