Uploaded byAthanasios Anastasiou
ITAB2010-Thresholding Correlation Matrices
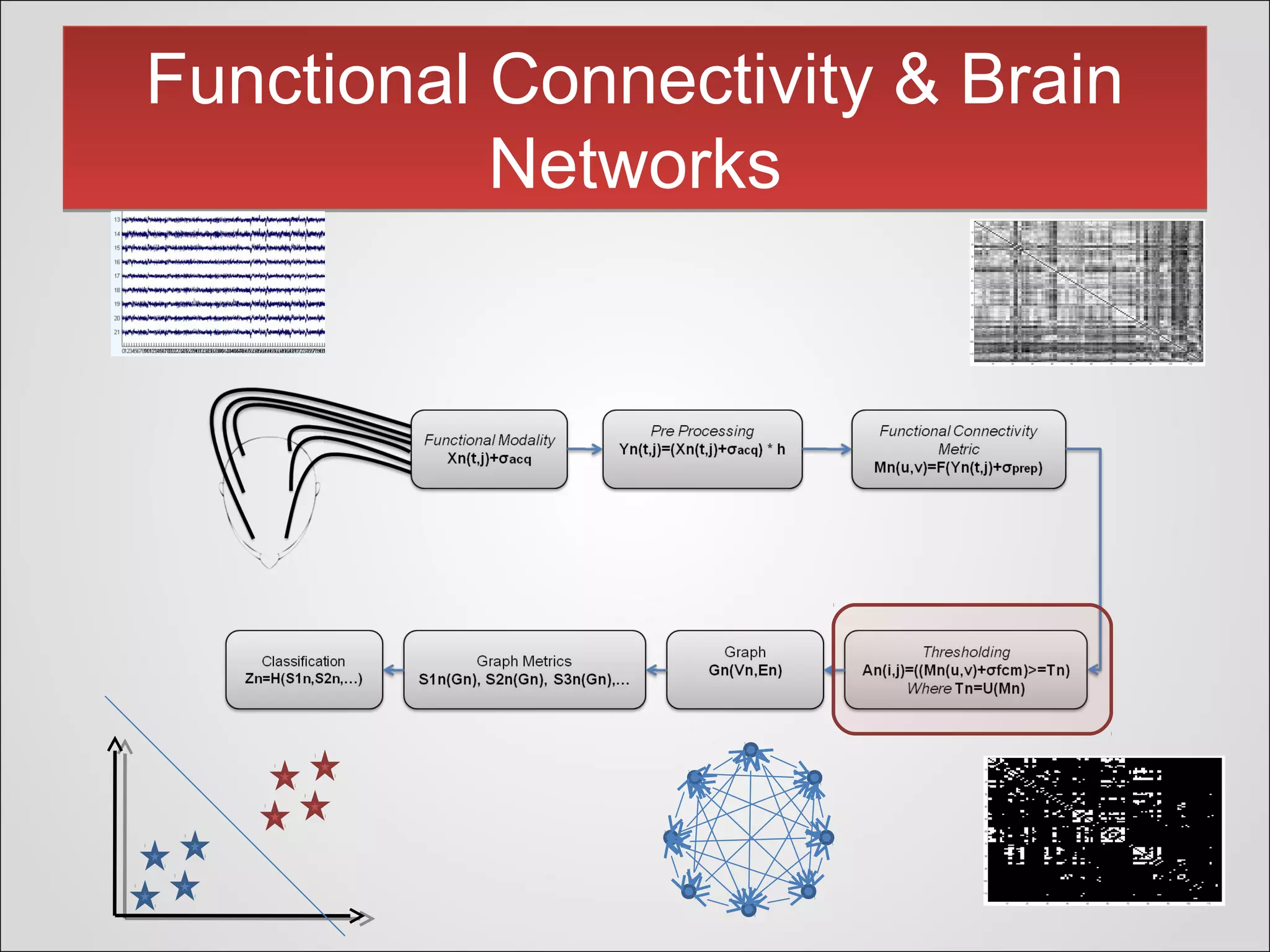
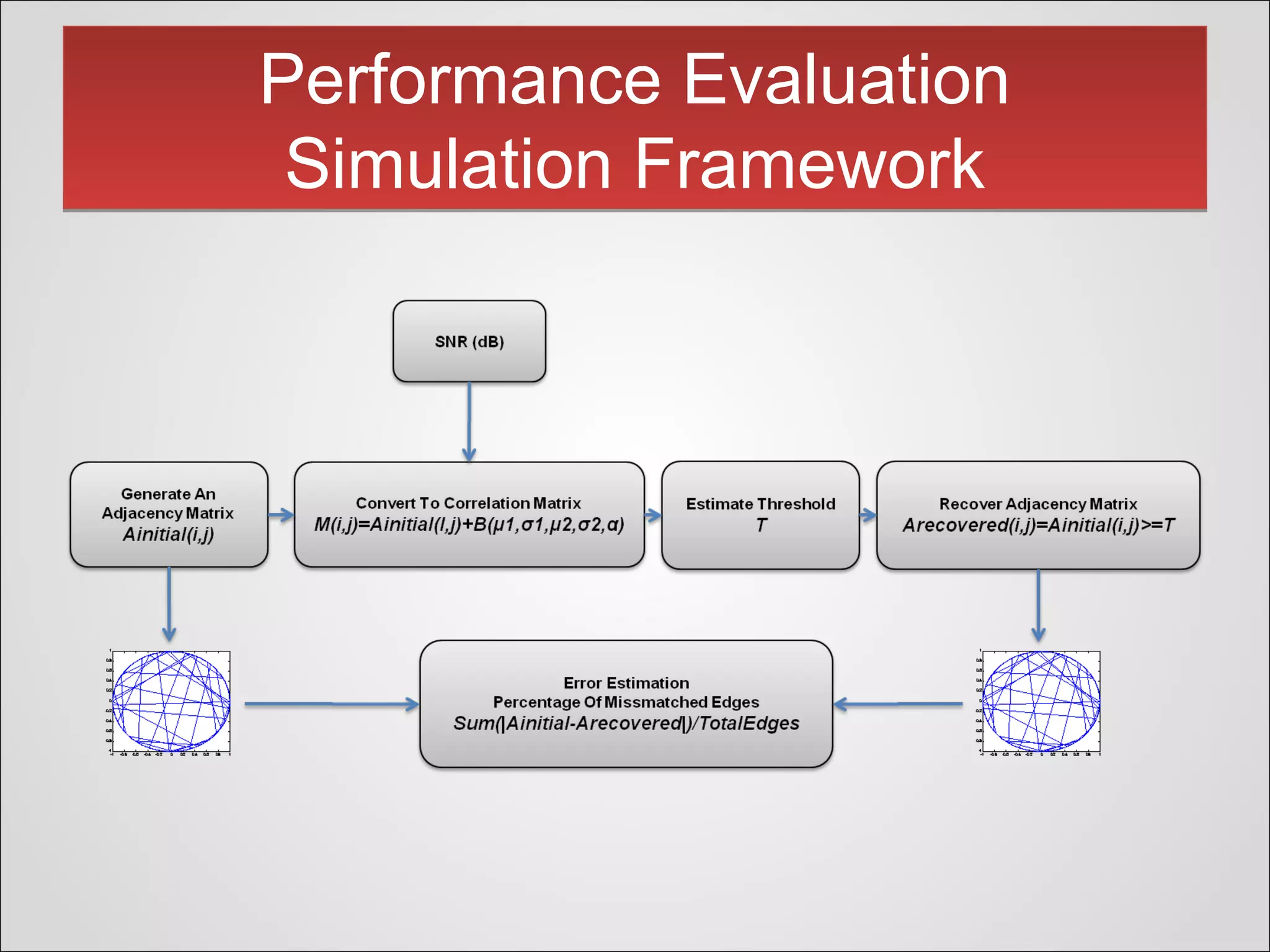
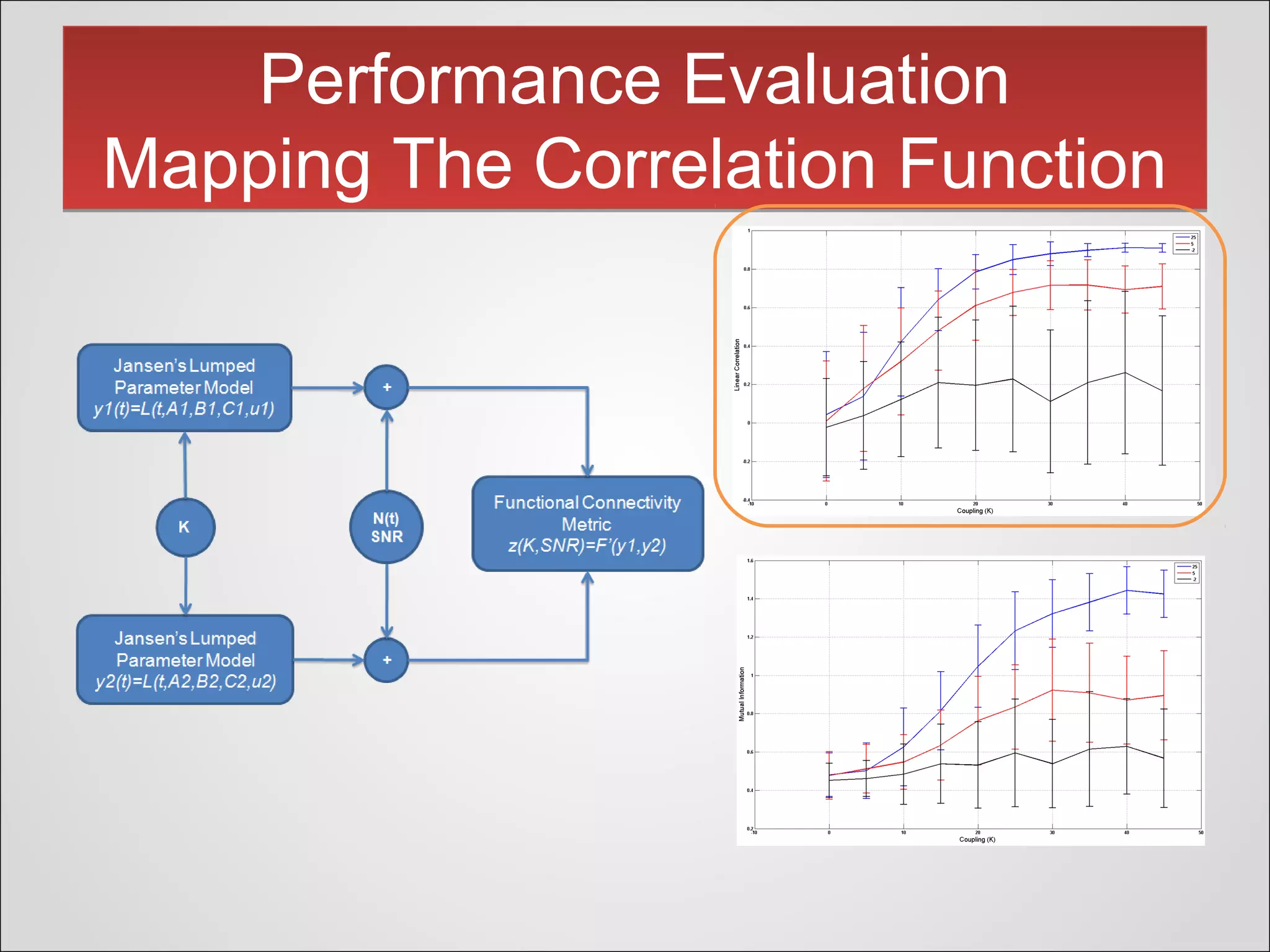
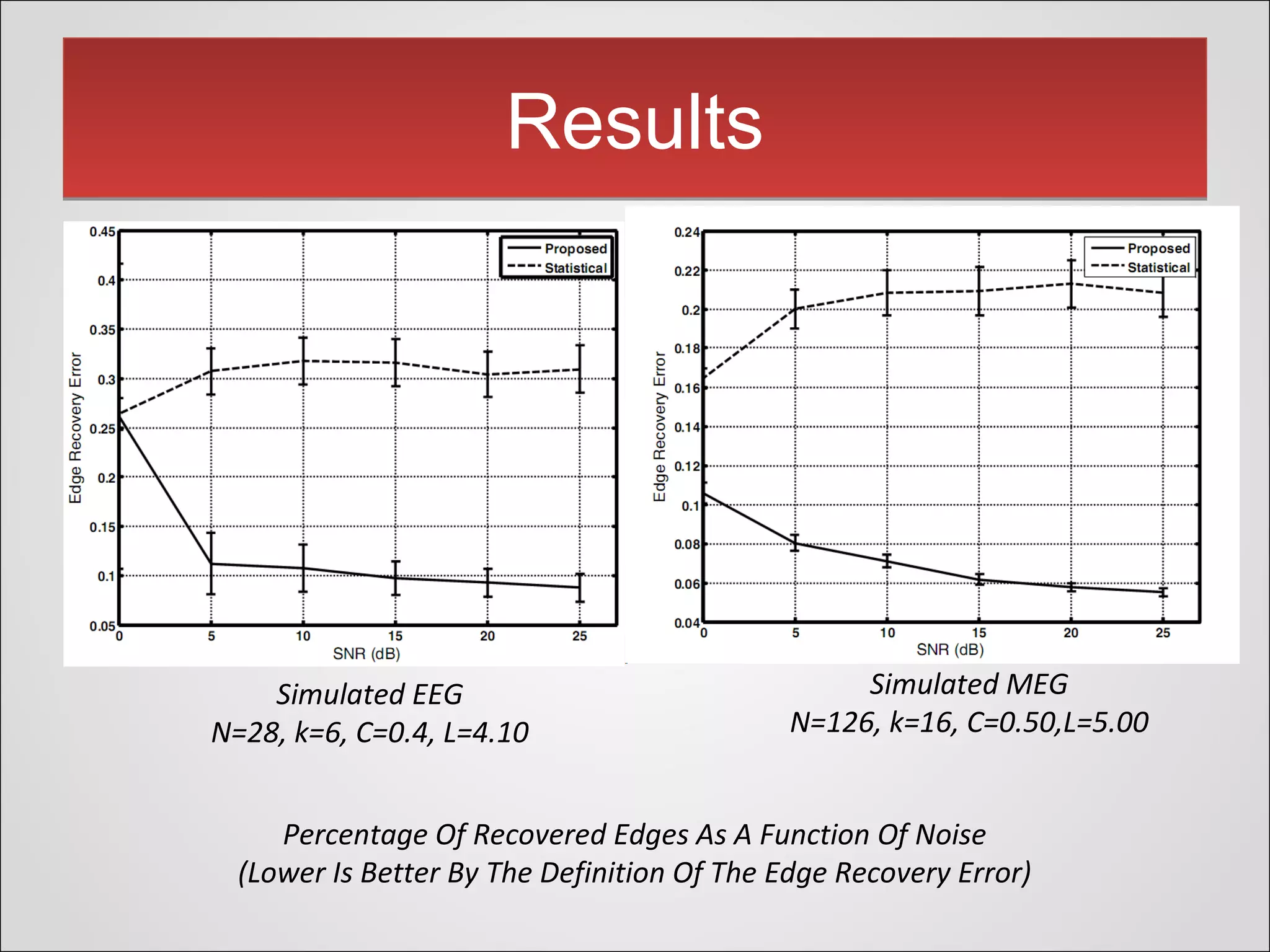
This document presents a novel thresholding method for analyzing functional connectivity networks in the brain, which is based on the subject's correlation matrix to identify strongly and weakly correlated pairs of channels. The proposed method utilizes a bimodal distribution to optimize the threshold value and demonstrates improved edge recovery in simulations compared to current techniques. The findings highlight the challenges of thresholding in low signal-to-noise ratio conditions and question the necessity of a threshold in some analyses.
More Related Content
ITAB2010-Thresholding Correlation Matrices
- 1. A Novel ThresholdingMethod For The Analysis Of Functional Connectivity Networks Of The Brain A Novel Thresholding Method For The Analysis Of Functional Connectivity Networks Of The Brain Athanasios Anastasiou, Emmanuel Ifeachor Signal Processing and Multimedia Communications Research Group University of Plymouth - UK
- 2. TopicsTopics • Functional Connectivity& Brain Networks • Proposed Thresholding Method • Performance Evaluation • Results
- 3. Functional Connectivity &Brain Networks Functional Connectivity & Brain Networks
- 4. ThresholdingThresholding Currently Used Methods •SetA Limit On The Maximum Number Of Neighbours •Arbitrary •Order The Values Of The Correlation Matrix And Select A Point Heuristically •Does This Correspond To The Underlying Effects? •Pick The Threshold Value That Generates Maximum Separation Between Groups •Advance Knowledge Of Subject Groups Correlation Matrix Adjacency Matrix (Affects Network Structure)
- 5. Proposed Thresholding MethodProposedThresholding Method • Based Only On A Subject’s Correlation Matrix • Single Threshold Implies Two Correlation Groups – Pairs Of Channels • Strongly Correlated • Weakly Correlated • Bimodal Distribution. – Five Parameters • μstrong, σstrong • μweak, σweak • α:Mixing Parameter
- 6. Proposed Thresholding MethodProposedThresholding Method Correlation Matrix M(i,j) Obtain Histogram H(M(i,j)) Select A Threshold Value Estimate True & False Positive Rates Fit A Bimodal (μS, σS, μW, σW, a)
- 7. Performance Evaluation Simulation Framework PerformanceEvaluation Simulation Framework
- 8. Performance Evaluation Simulation Framework PerformanceEvaluation Simulation Framework • Simulation – Adjacency Matrix Correlation Matrix • Contributing Factors – Underlying System Dynamics – Coupling – Correlation Function
- 9. Performance Evaluation Mapping TheCorrelation Function Performance Evaluation Mapping The Correlation Function
- 10. ResultsResults Percentage Of RecoveredEdges As A Function Of Noise (Lower Is Better By The Definition Of The Edge Recovery Error) Simulated EEG N=28, k=6, C=0.4, L=4.10 Simulated MEG N=126, k=16, C=0.50,L=5.00
- 11. Concluding RemarksConcluding Remarks •An Iterative, Subject Specific Process To Determine The Threshold Value • Recovers More Edges Than Currently Employed Techniques – Simulated Conditions • Thresholding Is Extremely Difficult Without Prior Information – Especially At Low SNRs • Is A Threshold Really Necessary?
Editor's Notes
- #4 The bigger picture of correlation analysis for functional connectivity Data are obtained from a patient with a degree of noise. They are preprocessed (and “distorted” because of the processing). The functional connectivity metric, returns information about the correlation between channels but again, there is the potential for some information to be lost. Consider for example the mismatches that are introduced when examining signals from non-linear systems with linear techniques.)
- #5 How is thresholding applied? How has it being carried out so far by others and what problems are associated with it?