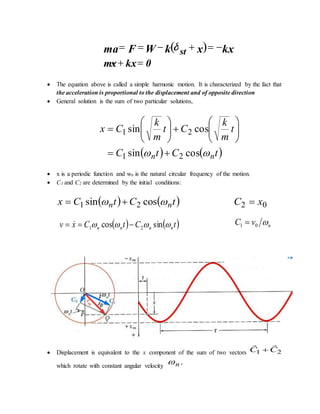
This document discusses mechanical vibrations, which occur when a system oscillates around an equilibrium position. It provides definitions for key vibration terms like period, frequency, amplitude, damping, and forced versus free vibrations. As examples, it examines the simple harmonic motion of a mass attached to a spring, and the motion of a simple pendulum through both approximate and exact solutions.

1. INTRODUCTION
 Mechanical vibration is the motion of a particle or body which oscillates about a position
of equilibrium. Most vibrations in machines and structures are undesirable due to
increased stresses and energy losses which accompany them.
 A mechanical vibration generally results when a system is displaced from a position of
stable equilibrium. The system tends to return to this position under the action of
restoring forces (either elastic forces, as in the case of a mass attached to a spring or
gravitational forces, as in the case of a pendulum )
 Time interval required for a system to complete a full cycle of the motion is the period of
the vibration.
 Number of cycles per unit time defines the frequency of the vibrations.
 Maximum displacement of the system from the equilibrium position is the amplitude of
the vibration
 When the motion is maintained by the restoring forces only, the vibration is described as
free vibration. When a periodic force is applied to the system, the motion is described as
forced vibration
 When the frictional dissipation of energy is neglected, the motion is said to be
undamped. Actually, all vibrations are damped to some degree.
 If a free vibration is only slightly damped, its amplitude slowly decreases until after a
certain time, the motion comes to a stop.
 If a damping is large enough to prevent any true vibration, the system slowly regains its
original position.
 A damped forces vibration is maintained as long as the periodic force which produces the
vibration is applied. The amplitude of the vibration however is affected by the magnitude
of the damping forces.

2. FREE VIBRATIONS OF A PARTICLE. SIMPLE HARMONIC MOTION
 Consider a body of a mass m attached to a spring of constant k ( Fiq a) . When the
particle is in static equilibrium, the forces acting on it are its weight W and the force T
exerted by the spring, of magnitude T = k st , where  st denotes the elongation of
the spring. Therefore
W = k st
 If a particle is displaced through a distance xm from its equilibrium position and released
with no velocity, the particle will undergo simple harmonic motion

3.  The equation above is called a simple harmonic motion. It is characterized by the fact that
the acceleration is proportional to the displacement and of opposite direction
 General solution is the sum of two particular solutions,
 x is a periodic function and wn is the natural circular frequency of the motion.
 C1 and C2 are determined by the initial conditions:
 Displacement is equivalent to the x component of the sum of two vectors
which rotate with constant angular velocity
   tCtC
t
m
k
Ct
m
k
Cx
nn  cossin
cossin
21
21














   tCtCx nn  cossin 21  02 xC 
21 CC


.n
 
0

kxxm
kxxkWFma st


   tCtCxv nnnn  sincos 21   nvC 01 

4. 

02
0
1
xC
v
C
n



Natural frequency


 2
1 n
n
nf
period
n
n



2
 Phase angle 
nxv  00
1
tan
  Amplitude 2
0
2
0 xvx nm 
   txx nm sin

5. SIMPLE PENDULUM ( APPROXIMATE SOLUTION)
 Results obtained for the spring-mass system can be applied whenever the resultant force
on a particle is proportional to the displacement and directed towards the equilibrium
position.
 Consider tangential components of acceleration and force for a simple pendulum,
 For small angles,
:tt maF 
0sin
sin




l
g
mlW


 
g
l
t
l
g
n
n
nm






2
2
sin
0




6. SIMPLE PENDULUM ( EXACT SOLUTION)
 An exact solution for leads to
which requires
numerical solution.
0sin  
l
g
 



2
0
22
sin2sin1
4




m
n
d
g
l







g
lK
n 

 2
2