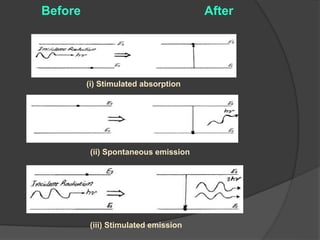
This document provides an overview of laser theory and applications across 4 chapters. Chapter 1 discusses the theory of lasing, including Einstein's theory of stimulated emission and how a population inversion enables light amplification in a laser medium. Chapter 2 will cover characteristics of laser beams. Chapter 3 will describe different types of laser sources. And Chapter 4 will discuss applications of laser technology.

1. Laser and its applications
Chapter (1): Theory of Lasing (2)
Chapter (2): Characteristics of laser beam ) (
Chapter (3): Types of laser sources ( )
Chapter (4): Laser applications ( )
Contents page

2. Chapter (1) Theory of Lasing
1.Introduction (Brief history of laser)
The laser is perhaps the most important optical device
to be developed in the past 50 years. Since its arrival in
the 1960s, rather quiet and unheralded outside the
scientific community, it has provided the stimulus to make
optics one of the most rapidly growing fields in science
and technology today.

3. The laser is essentially an optical amplifier. The word
laser is an acronym that stands for “light amplification
by the stimulated emission of radiation”. The theoretical
background of laser action as the basis for an optical
amplifier was made possible by Albert Einstein, as early
as 1917, when he first predicted the existence of a new
irradiative process called “stimulated emission”. His
theoretical work, however, remained largely unexploited
until 1954, when C.H. Townes and Co-workers
developed a microwave amplifier based on stimulated
emission radiation. It was called a maser.

4. Following the birth of the ruby and He-Ne lasers, others devices
followed in rapid succession, each with a different laser medium
and a different wavelength emission. For the greater part of the
1960s, the laser was viewed by the world of industry and
technology as scientific curiosity.
In 1960, T.H.Maiman built the first laser device (ruby
laser). Within months of the arrival of Maiman’s ruby laser,
which emitted deep red light at a wavelength of 694.3 nm,
A. Javan and associates developed the first gas laser (He-
Ne laser), which emitted light in both the infrared (at
1.15mm) and visible (at 632.8 nm) spectral regions..

5. 1.Einstein’s quantum theory of radiation
In 1916, according to Einstein, the interaction of
radiation with matter could be explained in terms of
three basic processes: spontaneous emission,
absorption and stimulated emission. The three
processes are illustrated and discussed in the
following:

6. Before After
(i) Stimulated absorption
ii) Spontaneous emission)
(iii) Stimulated emission

7. )ii) Spontaneous emission
Consider an atom (or molecule) of the material is existed
initially in an excited state E2 No external radiation is
required to initiate the emission. Since E2>E1, the atom will
tend to spontaneously decay to the ground state E1, a
photon of energy h =E2-E1 is released in a random
direction as shown in (Fig. 1-ii). This process is called
“spontaneous emission ”
Note that; when the release energy difference (E2-E1) is
delivered in the form of an e.m wave, the process called
"radiative emission" which is one of the two possible ways
“non-radiative” decay is occurred when the energy
difference (E2-E1) is delivered in some form other than e.m
radiation (e.g. it may transfer to kinetic energy of the
surrounding)

8. (iii) Stimulated emission
Quite by contrast “stimulated emission” (Fig. 1-iii)
requires the presence of external radiation when an
incident photon of energy h =E2-E1 passes by an atom
in an excited state E2, it stimulates the atom to drop or
decay to the lower state E1. In this process, the atom
releases a photon of the same energy, direction, phase
and polarization as that of the photon passing by, the
net effect is two identical photons (2h) in the place of
one, or an increase in the intensity of the incident beam.
It is precisely this processes of stimulated emission
that makes possible the amplification of light in lasers.

9. Growth of Laser Beam
Atoms exist most of the time in one of a number of
certain characteristic energy levels. The energy level
or energy state of an atom is a result of the energy
level of the individual electrons of that particular
atom. In any group of atoms, thermal motion or
agitation causes a constant motion of the atoms
between low and high energy levels. In the absence
of any applied electromagnetic radiation the
distribution of the atoms in their various allowed
states is governed by Boltzman’s law which states
that:
The theory of lasing

10. if an assemblage of atoms is in state of thermal
equilibrium at an absolute temp. T, the number of atoms
N2 in one energy level E2 is related to the number N1 in
another energy level E1 by the equation.
Where E2>E1 clearly N2<N1
K Boltzmann’s constant = 1.38x10-16 erg / degree
= 1.38x10-23 j/K
T the absolute temp. in degrees Kelvin
KT/)1E2E(
12 eNN 


11. At absolute zero all atoms will be in the ground
state. There is such a lack of thermal motion among the
electrons that there are no atoms in higher energy
levels. As the temperature increases atoms change
randomly from low to the height energy states and back
again. The atoms are raised to high energy states by
chance electron collision and they return to the low
energy state by their natural tendency to seek the
lowest energy level. When they return to the lower
energy state electromagnetic radiation is emitted. This
is spontaneous emission of radiation and because of its
random nature, it is incoherent

12. As indicated by the equation, the number of atoms
decreases as the energy level increases. As the temp
increases, more atoms will attain higher energy levels.
However, the lower energy levels will be still more
populated.
Einstein in 1917 first introduced the concept of
stimulated or induced emission of radiation by atomic
systems. He showed that in order to describe completely
the interaction of matter and radiative, it is necessary to
include that process in which an excited atom may be
induced by the presence of radiation emit a photon and
decay to lower energy state.

13. An atom in level E2 can decay to level E1 by emission
of photon. Let us call A21 the transition probability per
unit time for spontaneous emission from level E2 to
level E1. Then the number of spontaneous decays per
second is N2A21, i.e. the number of spontaneous decays
per second=N2A21.
In addition to these spontaneous transitions, there
will induced or stimulated transitions. The total rate to
these induced transitions between level 2 and level 1 is
proportional to the density (U) of radiation of frequency
, where
 = ( E2-E1 )/h , h Planck's const.

14. Let B21 and B12 denote the proportionality constants
for stimulated emission and absorption. Then number of
stimulated downward transition in stimulated emission
per second = N2 B21 U
similarly , the number of stimulated upward transitions
per second = N1 B12 U
The proportionality constants A and B are known as the
Einstein A and B coefficients. Under equilibrium
conditions we have

15. by solving for U (density of the radiation) we obtain
U [N1 B12- N2 B21 ] = A21 N2
212121
212
BNBN
AN
)(U


N2 A21 + N2 B21 U =N1 B12 U
SP ST
A b

16. 







1
)(
2
1
21
12
21
21
N
N
B
B
B
A
U 
KT/hKT/)EE(
1
2
ee
N
N 12 










1e
B
B
B
A
)(U
KT/h
21
12
21
21
According to Planck’s formula of radiation
 1e
1
c
h8
)(U KT/h3
3


  )2)
)1)

17. from equations 1 and 2 we have
B12=B21 (3)
213
3
21 B
c
h8
A


equation 3 and 4 are Einstein’s relations.
Thus for atoms in equilibrium with thermal
radiation.
)4 (
21
21
212
212
A
)(UB
AN
)(UBN
emissioneoustanspon
emissionstimulate 



from equation 2 and 4

18.  1e
1
c
h8
h8
c
)(U
h8
c
emission.spon
emission.stim
KT/h3
3
3
3
3
3








 1e
1
emission.spon
emission.stim
KT/h

 
(5)
Accordingly, the rate of induced emission is extremely
small in the visible region of the spectrum with
ordinary optical sources ( T10 3 K (.

19. Hence in such sources, most of the radiation is
emitted through spontaneous transitions. Since these
transitions occur in a random manner, ordinary sources
of visible radiation are incoherent.
On the other hand, in a laser the induced transitions
become completely dominant. One result is that the
emitted radiation is highly coherent. Another is that the
spectral intensity at the operating frequency of the laser
is much greater than the spectral intensities of ordinary
light sources .

20. Amplification in a Medium
Consider an optical medium through which radiation is
passing. Suppose that the medium contains atoms in various
energy levels E1, E2, E3,….let us fitt our attention to two levels
E1& E2 where E2>E1 we have already seen that the rate of
stimulated emission and absorption involving these two levels
are proportional to N2B21&N1B12 respectively. Since B21=B12,
the rate of stimulated downward transitions will exceed that of
the upward transitions when N2>N1,.i.e the population of the
upper state is greater than that of the lower state such a
condition is condrary to the thermal equilibrium distribution
given by Boltzmann’s low. It is termed a population inversion.
If a population inversion exist, then a light beam will increase
in intensity i.e. it will be amplified as it passes through the
medium. This is because the gain due to the induced emission
exceeds the loss due to absorption.

21. x
,o eII 
 
gives the rate of growth of the beam intensity in the
direction of propagation,an is the gain constant at
frequency

22. Quantitative Amplification of light
In order to determine quantitatively the amount of
amplification in a medium we consider a parallel beam
of light that propagate through a medium enjoying
population inversion. For a collimated beam, the
spectral energy density U is related to the intensity 
in the frequency interval  to  +  by the formula.

23. Due to the Doppler effect and other line-broadening
effects not all the atoms in a given energy level are
effective for emission or absorption in a specified
frequency interval. Only a certain number N1 of the N1
atoms at level 1 are available for absorption. Similarly of
the N2 atoms in level 2, the number  N2 are available for
emission. Consequently, the rate of upward transitions is
given by:
c
IU

 
v
I
U 
1L
I
U


c
I
U 

24. 221221 N)c/I(BNUB  
and the rate of stimulated or induced downward
transitions is given by:
Now each upward transition subtracts a quantum energy
h from the beam. Similarly, each downward transition
adds the same amount therefore the net time rate of
change of the spectral energy density in the interval  is
given by
  U)NBNB(h)U(
dt
d
112221
where (h B NU)= the rate of transition of quantum
energy
c
I
)NBNB(h)
c
I
(
dt
d
112221



25. In time dt the wave travels a distance dx = c dt i.e
dx
c
dt
1
 then







 IB)
NN
(
c
h
dx
dI
21
12


 I
dx
dI
dx
I
dI




x.
,o
eII 



26. in which  is the gain constant at frequency  it is given
by:
12
12
B)
NN
(
c
h






an approximate expression is
1212max B)NN(
c
h



  being the line width

27. Doppler width
This is one of the few causes seriously affecting equally
both emission and absorption lines. Let all the atoms emit
light of the same wavelength. The effective wavelength
observed from those moving towards an observer is
diminished and for those atoms moving away it is increased
in accordance with Doppler’s principle.
When we have a moving source sending out waves
continuously it moves. The velocity of the waves is often not
changed but the wavelength and frequency as noted by
stationary observed alter.

28. Thus consider a source of waves moving towards an
observer with velocity v. Then since the source is moving
the waves which are between the source and the
observer will be crowded into a smaller distance than if
the source had been at rest. If the frequency is o , then
in time t the source emit ot waves. If the frequency had
been at rest these waves would have occupied a length
AB. But due to its motion the source has caused a
distance vt, hence these ot waves are compressed into
a length where
BA

29. vtBAAB

vttt
oo thus
o
v


o
v


)
v
1(
o


Observer
)
c
v
1(

)
c
v
1(
cc
o




where n=c

30. )
c
v
1(
cc
o




)
c
v
1(o

c
v
1
o



c
v
o
o



)(
c
v o
o




31. Evaluation of Doppler half width:
According to Maxwelliam distribution of velocities, from
the kinetic theory of gasses, the probability that the velocity
will be between v and v+v is given by:
dve
B 2Bv

So that the fraction of atoms whose their velocities lie
between v and v+ v is given by the following equation
ve
B
N
)(N 2
Bv



 
where B= m = molecular weight, K=gas constant,
T=absolute temp
KT2
m

32. Substituting for v in the last equation from equation (1)
and since the intensity emitted will depend on the
number of atoms having the velocity in the region v and
 vv  then, i. e.
N
)(N
)(I


I() = const
.
2)o(
2
o
2c
B
e



 = 
at
I(
=)I
=const
 ))=  max= const

33. There for
) max
2)o(
2
o
2c
B
e



2
1
e
I
)2/(I 4
2
2
o
2c
B
max
o





being the half width of the spectral line it is the width at
2
Imax , then
4
c
B2ln
2
2
o
2





 2ln
m
kT2
c
2 o