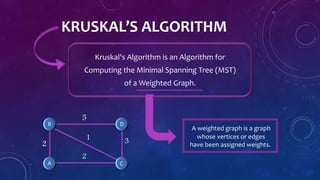
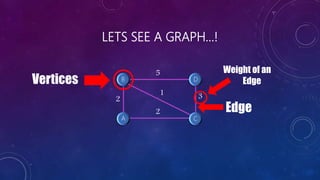
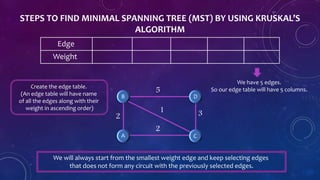
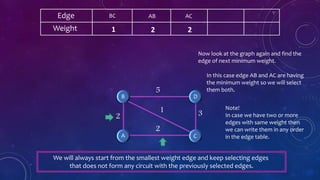
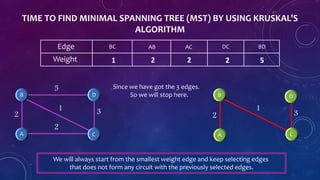
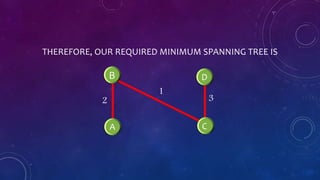
The document presents a presentation on Kruskal's Algorithm, which is used to compute the minimal spanning tree (MST) of a weighted graph. It details Joseph Kruskal's contributions to mathematics and computer science, including the introduction of his algorithm. The process of using Kruskal's Algorithm involves selecting the smallest weight edges while avoiding the formation of circuits until the MST is completed.

2. BENAZIR BHUTTO SHAHEED
UNVERSITY
Department of Computer Science
Under the guidance of:
Sir Ali Aurangzeb

3. Kruskal’s
Algorithm
PRESENTED BY:
ABDUL MOIZ KHATRI
3rd SEMESTER – Batch 6th
BECHALORS OF COMPUTER SCIENCE
PRESENTATION ON:

4. JOSEPH KRUSKAL
• Joseph Kruskal was an American Mathematician, Statistician and
Computer Scientist.
• He was born in January 29, 1928.
• He was a student at the University of Chicago earning a Bachelor of
Science in Mathematics in the year of 1948 and a Master of Science in
Mathematics in the following year 1949.
• After his time at the University of Chicago, Kruskal attended Princeton
University, where he completed his Ph.D. in Mathematics in the year of 1954.
• In Statistics, Kruskal's most influential work is his seminal contribution to the formulation
of Multidimensional Scaling.
• In Computer Science, his best known work is Kruskal's Algorithm for computing the Minimal
Spanning Tree (MST) of a weighted graph.
• He died in September 19, 2010.

5. WHAT IS AN ALGORITHM?
An Algorithm is a step-by-step procedure
to solve a given problem.

6. KRUSKAL’S ALGORITHM

7. Kruskal's Algorithm is an Algorithm for
Computing the Minimal Spanning Tree (MST)
of a Weighted Graph.
KRUSKAL’S ALGORITHM
A Minimal Spanning Tree is a Spanning Tree of
a connected, undirected graph which connects
all the vertices together with the Minimal total weightage
for its edges and it always have V-1 Edges.
A
B
C
D
1 32

8. Kruskal's Algorithm is an Algorithm for
Computing the Minimal Spanning Tree (MST)
of a Weighted Graph.
KRUSKAL’S ALGORITHM
A weighted graph is a graph
whose vertices or edges
have been assigned weights.
A
B
C
D
1 3
2
2
5

9. LETS SEE A GRAPH…!
A
B
C
D
1 3
2
2
5
Vertices
Edge
Weight of an
Edge

10. HOW TO FIND MINIMAL SPANNING TREE (MST) BY USING KRUSKAL’S
ALGORITHM?
We will always start from the
smallest weight edge and keep
selecting edges that does not
form any circuit with the
previously selected edges.
REMEMBER….

11. A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
We have 5 edges.
So our edge table will have 5 columns.Create the edge table.
(An edge table will have name
of all the edges along with their
weight in ascending order)
Edge
Weight
STEPS TO FIND MINIMAL SPANNING TREE (MST) BY USING KRUSKAL’S
ALGORITHM

12. Edge
Weight

13. A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
Edge
Weight
Now look at the graph and fill the
1st column with the edge of minimum weight.
In this case edge BC is of least weight
so we will select it.
BC
1
Now look at the graph again and find the
edge of next minimum weight.
In this case edge AB and AC are having
the minimum weight so we will select
them both.
Note!
In case we have two or more
edges with same weight then
we can write them in any order
in the edge table.
AB
2
AC
2

14. A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
Edge
Weight
BC
1
Now look at the graph again and find the
edge of next minimum weight.
In this case edge AB and AC are having
the minimum weight so we will select
them both.
Note!
In case we have two or more
edges with same weight then
we can write them in any order
in the edge table.
AB
2
AC
2

15. A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
Edge
Weight
BC
1
AB
2
AC
2
Now look at the graph again and
find the edge of next minimum edge.
In this case edge DC has the
minimum weight so we will select it.
DC
2
Now look at the graph again
and find the edge of next
minimum edge.
In this case edge BD has the
minimum weight so we will
select it.
BD
5

16. A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
TIME TO FIND MINIMAL SPANNING TREE (MST) BY USING KRUSKAL’S
ALGORITHM
Edge
Weight
BC
1
AB
2
AC
2
DC
2
BD
5
Note! Our graph has 4 vertices.
So, our MST will have 3 edges.

17. We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
TIME TO FIND MINIMAL SPANNING TREE (MST) BY USING KRUSKAL’S
ALGORITHM
Edge
Weight
BC
1
AB
2
AC
2
DC
2
BD
5
1 is the smallest weight.
So we will select edge BC.
B
C
1
A
B
C
D
1 3
2
2
5

18. A
2
A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
TIME TO FIND MINIMAL SPANNING TREE (MST) BY USING KRUSKAL’S
ALGORITHM
Edge
Weight
BC
1
AB
2
AC
2
DC
2
BD
5
2 is the next smallest
weight and edge AB does
not form a circuit with the
previously selected edges.
So we will select it.
B
C
1

19. A
2
A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
TIME TO FIND MINIMAL SPANNING TREE (MST) BY USING KRUSKAL’S
ALGORITHM
Edge
Weight
BC
1
AB
2
AC
2
DC
2
BD
5
2 is the smallest weight.
But if we select edge AC
then it will form a circuit. So
we are going to reject edge AC.
B
C
1

20. D
3
A
2
A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
TIME TO FIND MINIMAL SPANNING TREE (MST) BY USING KRUSKAL’S
ALGORITHM
Edge
Weight
BC
1
AB
2
AC
2
DC
2
BD
5
3 is the next smallest weight and
edge DC does not form a circuit
with the previously selected edges.
So we will select it.
B
C
1

21. D
3
A
2
A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
TIME TO FIND MINIMAL SPANNING TREE (MST) BY USING KRUSKAL’S
ALGORITHM
Edge
Weight
BC
1
AB
2
AC
2
DC
2
BD
5
3 is the next smallest weight and
edge DC does not form a circuit
with the previously selected edges.
So we will select it.
B
C
1

22. D
3
A
2
A
B
C
D
1 3
2
2
5
We will always start from the smallest weight edge and keep selecting edges
that does not form any circuit with the previously selected edges.
TIME TO FIND MINIMAL SPANNING TREE (MST) BY USING KRUSKAL’S
ALGORITHM
Edge
Weight
BC
1
AB
2
AC
2
DC
2
BD
5
B
C
1
Since we have got the 3 edges.
So we will stop here.

23. THEREFORE, OUR REQUIRED MINIMUM SPANNING TREE IS
D
3
A
2
B
C
1

24. QUERIES
SESSION

25. THANKS
ALOT…..