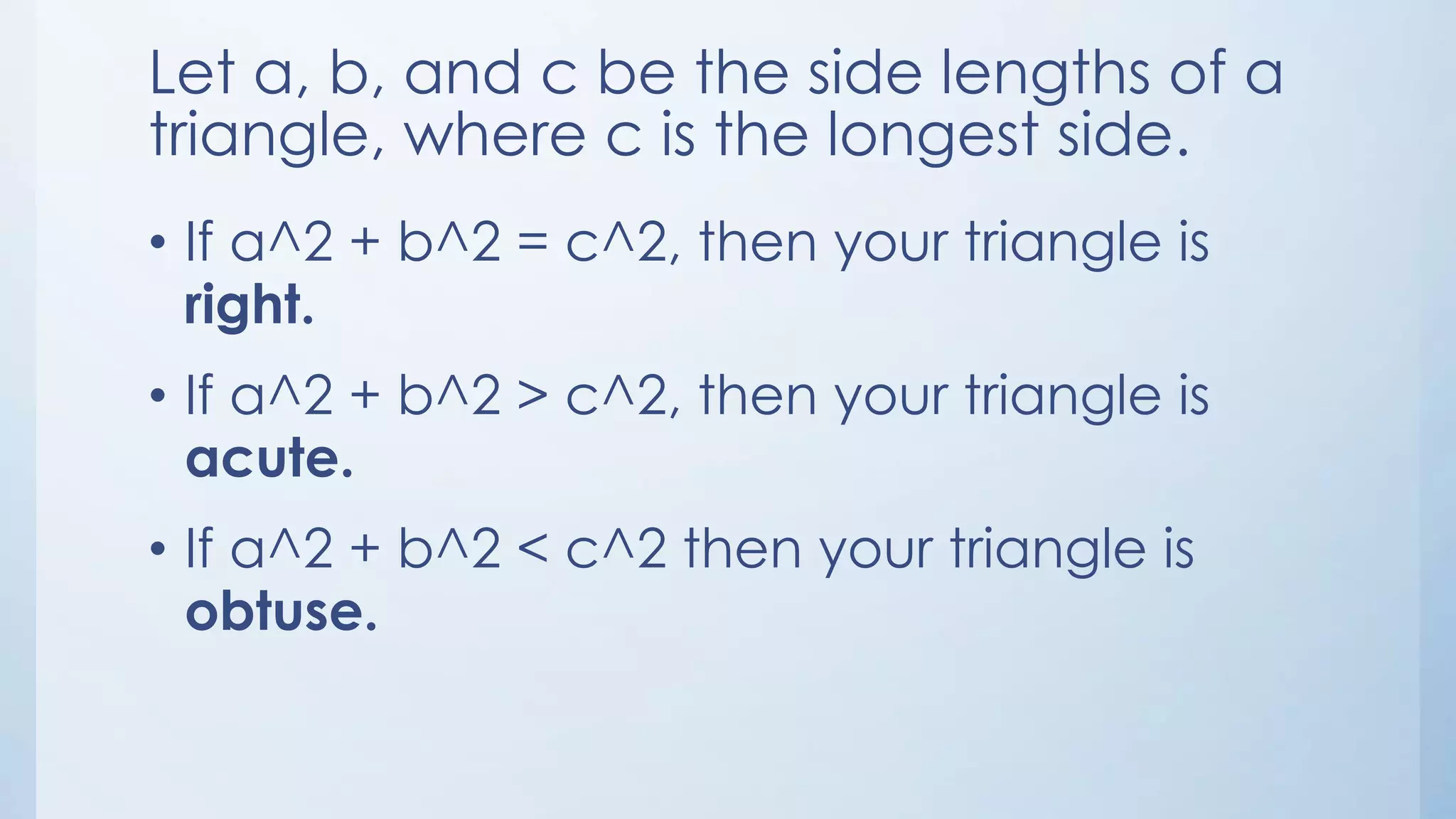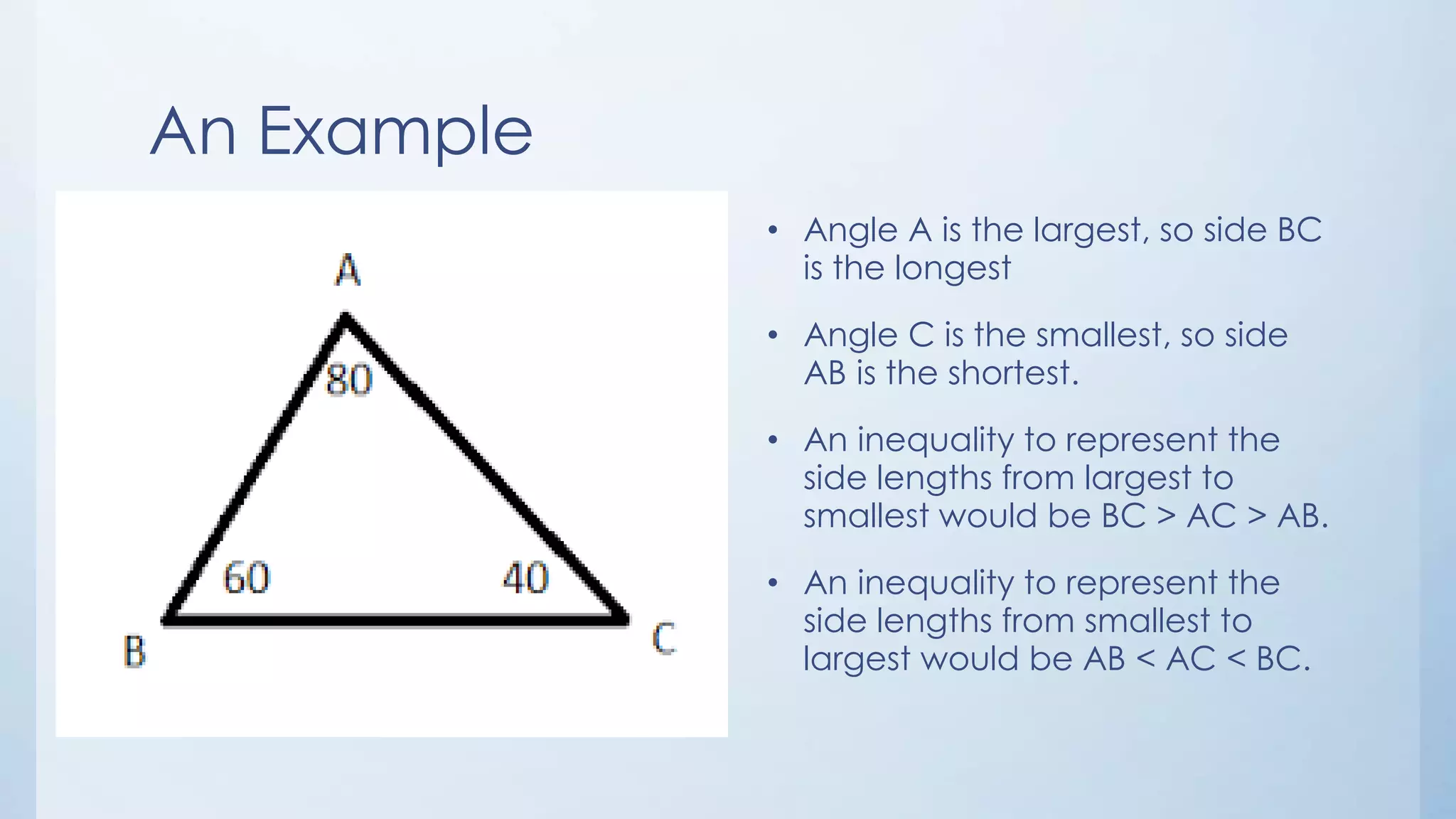
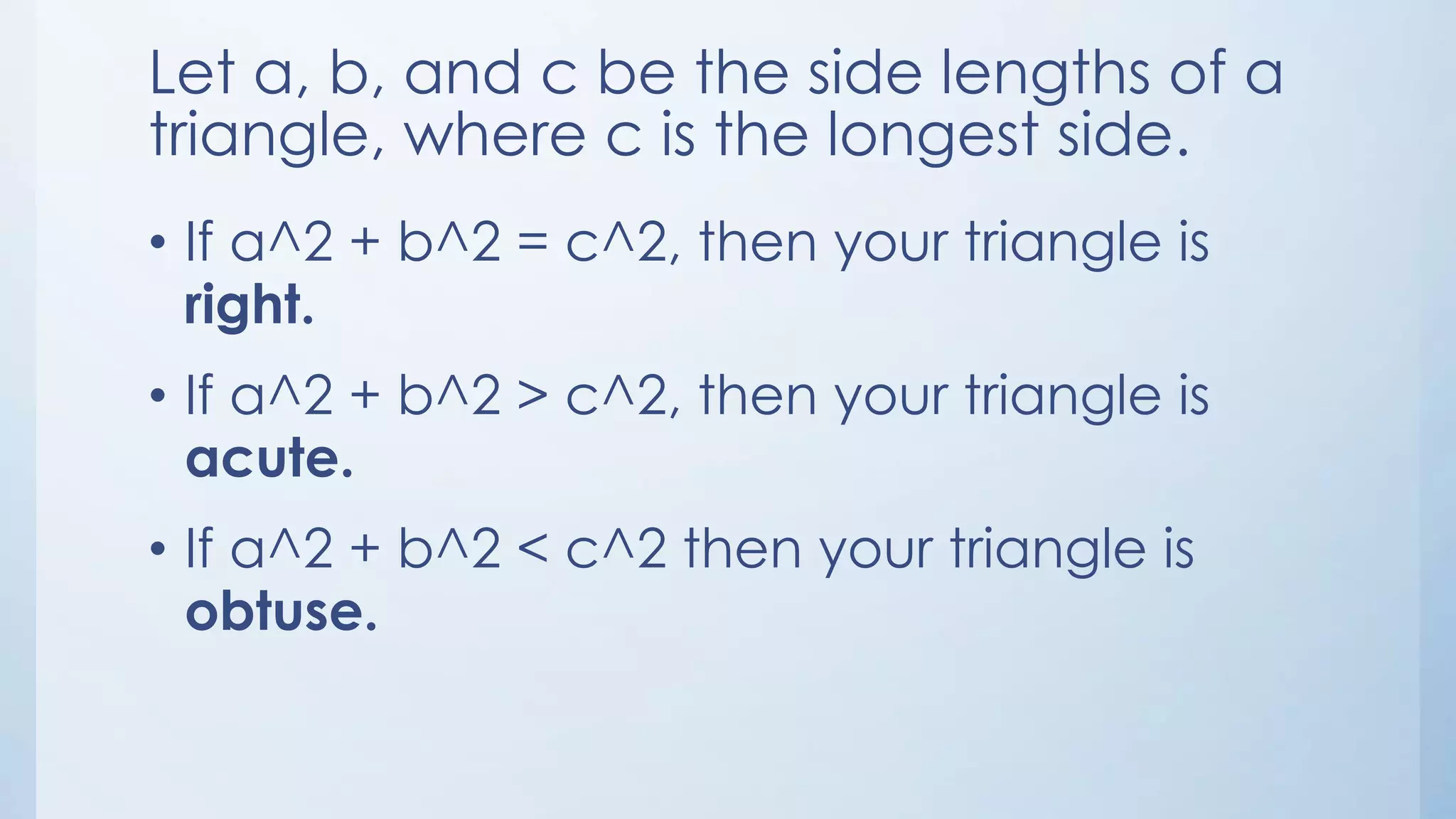
The document discusses the relationships between angles and sides in triangles. The longest side is opposite the largest angle, and the shortest side is opposite the smallest angle. Triangles can be classified as right, acute, or obtuse based on comparing the sum of the squares of two sides to the square of the third side - right if equal, acute if greater than, and obtuse if less than. Examples are given to demonstrate classifying triangles as acute or obtuse.

1. Angles and Sides of
a Triangle
How They Are Related 

2. The Relationship
• In a triangle, the longest side is across from
the largest angle.
• This also means that the shortest side is
across from the smallest angle.

3. An Example
• Angle A is the largest, so side BC
is the longest
• Angle C is the smallest, so side
AB is the shortest.
• An inequality to represent the
side lengths from largest to
smallest would be BC > AC > AB.
• An inequality to represent the
side lengths from smallest to
largest would be AB < AC < BC.

4. You can also classify a
triangle based on what
you know about its sides
and angles.

5. Let a, b, and c be the side lengths of a
triangle, where c is the longest side.
• If a^2 + b^2 = c^2, then your triangle is
right.
• If a^2 + b^2 > c^2, then your triangle is
acute.
• If a^2 + b^2 < c^2 then your triangle is
obtuse.

6. Classify each triangle as being
acute, obtuse, or right.
• Triangle with sides of 8 mm, 8
mm, and 10 mm
• 8^2 + 8^2 = 64 + 64 = 128
• 10^2 = 100
• Since 128 > 100, this is an
ACUTE triangle.
• Triangle with sides of 2 ft, 5 ft,
and 12 ft
• 2^2 + 5^2 = 4 + 25 = 29
• 12^2 = 144
• Since 29 < 144, this is an
OBTUSE triangle.