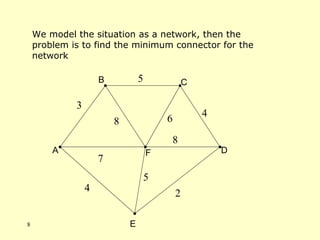
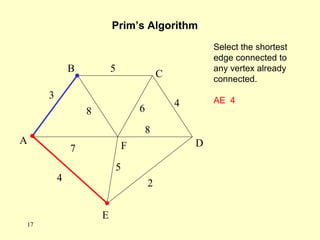
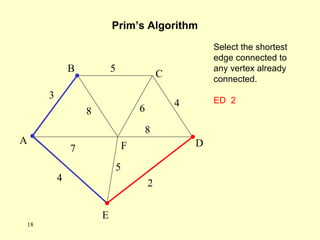
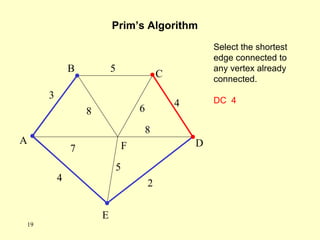
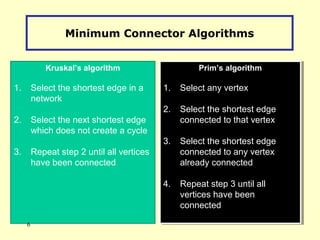
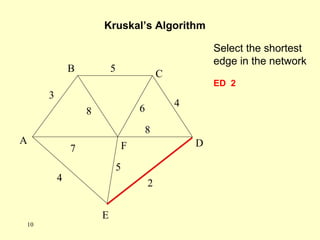
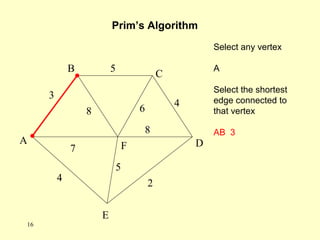
- A minimum spanning tree (MST) connects all nodes in a graph with the minimum total edge weight while avoiding cycles. - There are different algorithms that can find an MST, such as Kruskal's algorithm and Prim's algorithm, which were introduced in the document. - Kruskal's algorithm works by sorting the edges by weight and building the MST by adding the shortest edges that do not create cycles. Prim's algorithm grows the MST from an initial node by always adding the shortest edge connected to the current MST.

1. Minimum spanning treesMinimum spanning trees
1

2. MST
A minimum spanning tree connects all nodes in a given graph
A MST must be a connected and undirected graph
A MST can have weighted edges
Multiple MSTs can exist within a given undirected graph
Multiple MSTs can be generated depending on which algorithm is
used
If you wish to have an MST start at a specific node
However, if there are weighted edges and all weighted edges are
unique, only one MST will exist
2

3. Borůvka’s Algorithm
• The first MST Algorithm was created by
Otakar Borůvka in 1926
• The algorithm was used to create efficient
connections between the electricity
network in the Czech Republic
• No longer used since Prim’s and Kruskal’s
algorithms were discovered
3

4. Prim’s Algorithm
• Initially discovered in 1930 by Vojtěch
Jarník, then rediscovered in 1957 by
Robert C. Prim
• Similar to Dijkstra’s Algorithm regarding a
connected graph
• Starts off by picking any node within the
graph and growing from there
4

5. Kruskal’s Algorithm
• Created in 1957 by Joseph Kruskal
• Finds the MST by taking the smallest weight in the graph
and connecting the two nodes and repeating until all
nodes are connected to just one tree
• This is done by creating a priority queue using the
weights as keys
• Each node starts off as it’s own tree
• While the queue is not empty, if the edge retrieved
connects two trees, connect them, if not, discard it
• Once the queue is empty, you are left with the minimum
spanning tree
5

6. Minimum Connector Algorithms
Kruskal’s algorithm
1. Select the shortest edge in a
network
2. Select the next shortest edge
which does not create a cycle
3. Repeat step 2 until all vertices
have been connected
Prim’s algorithm
1. Select any vertex
2. Select the shortest edge
connected to that vertex
3. Select the shortest edge
connected to any vertex
already connected
4. Repeat step 3 until all
vertices have been
connected
Prim’s algorithm
1. Select any vertex
2. Select the shortest edge
connected to that vertex
3. Select the shortest edge
connected to any vertex
already connected
4. Repeat step 3 until all
vertices have been
connected
6

7. A cable company want to connect five villages to their network
which currently extends to the market town of Addis Ababa. What
is the minimum length of cable needed?
Addis Hawassa
Adama Awash
Dilla
Wolita
2
7
4
5
8 6
4
5
3
8
Example
7

8. We model the situation as a network, then the
problem is to find the minimum connector for the
network
A F
B C
D
E
2
7
4
5
8 6
4
5
3
8
8

9. A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
List the edges in
order of size:
ED 2
AB 3
AE 4
CD 4
BC 5
EF 5
CF 6
AF 7
BF 8
CF 8
Kruskal’s Algorithm
9

10. Select the shortest
edge in the network
ED 2
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
10

11. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
11

12. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4 (or AE 4)
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
12

13. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4
AE 4
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
13

14. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4
AE 4
BC 5 – forms a cycle
EF 5
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
14

15. All vertices have been
connected.
The solution is
ED 2
AB 3
CD 4
AE 4
EF 5
Total weight of tree: 18
Kruskal’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
15

16. A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
Select any vertex
A
Select the shortest
edge connected to
that vertex
AB 3
Prim’s Algorithm
16

17. A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
Select the shortest
edge connected to
any vertex already
connected.
AE 4
Prim’s Algorithm
17

18. Select the shortest
edge connected to
any vertex already
connected.
ED 2
Prim’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
18

19. Select the shortest
edge connected to
any vertex already
connected.
DC 4
Prim’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
19

20. Select the shortest
edge connected to
any vertex already
connected.
EF 5
Prim’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
20

21. Prim’s Algorithm
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
All vertices have been
connected.
The solution is
AB 3
AE 4
ED 2
DC 4
EF 5
Total weight of tree: 18
21

22. •Both algorithms will always give solutions with the
same length.
•They will usually select edges in a different order
•Occasionally they will use different edges – this
may happen when you have to choose between
edges with the same length. In this case there is
more than one minimum connector for the
network.
Some points to note
22

23. Questions?
23