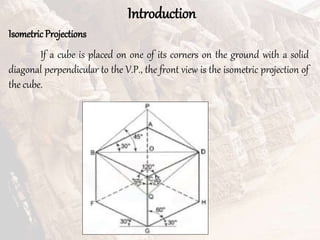
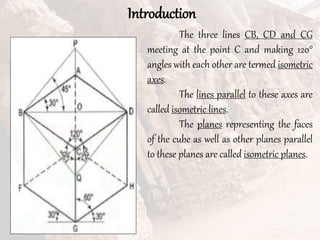
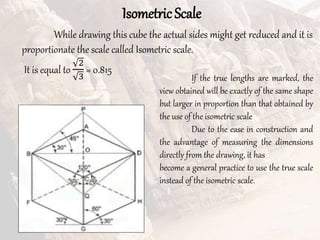
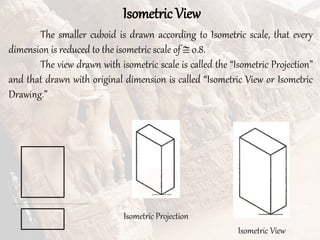
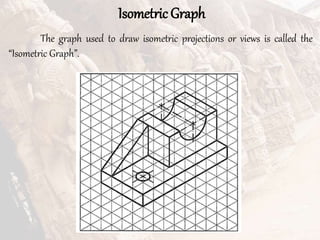
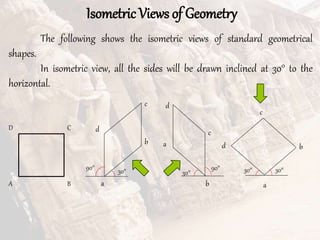
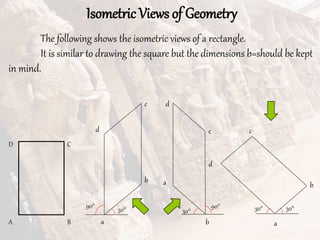
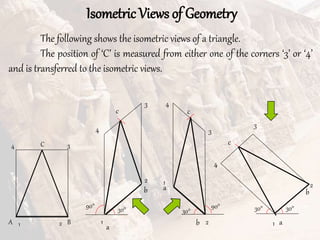
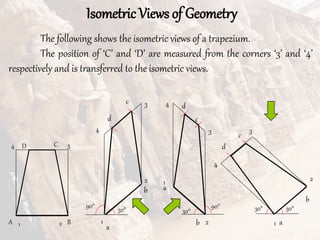
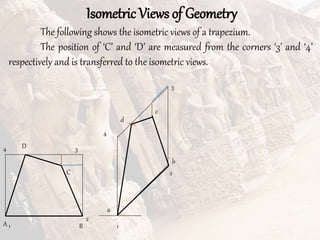
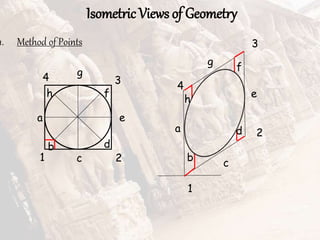
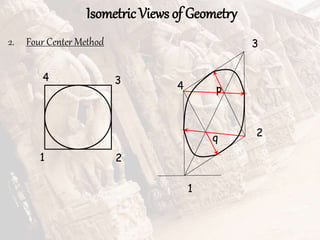
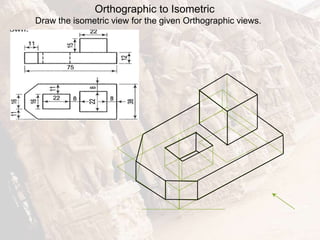
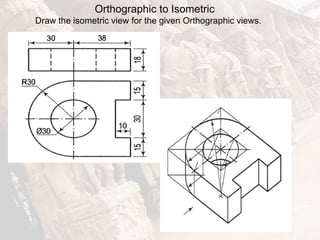
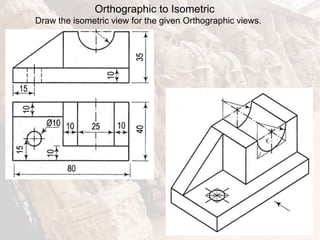
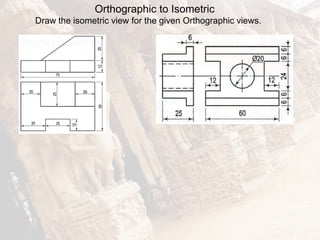
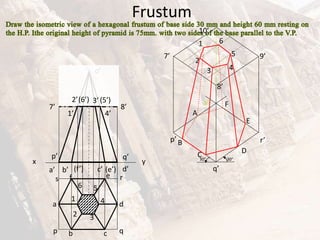
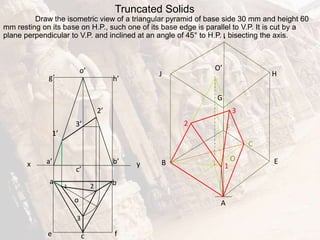
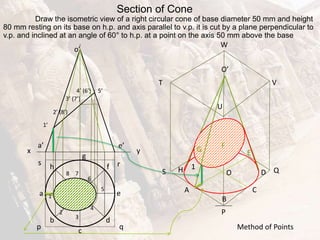
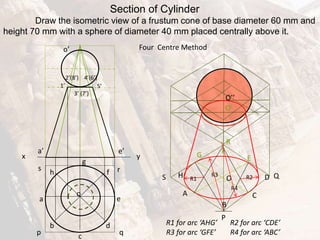
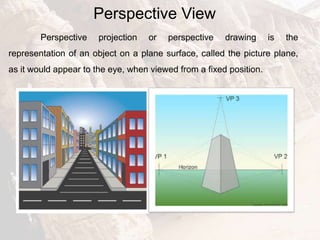
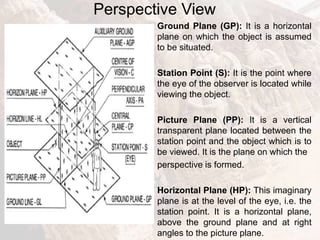
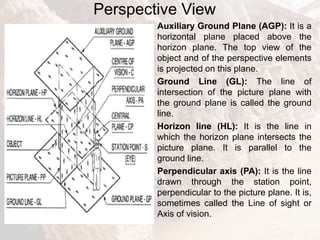
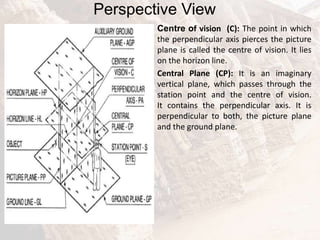
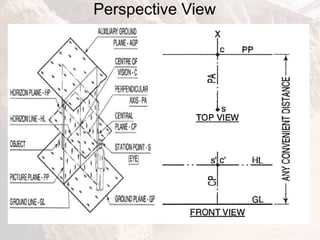
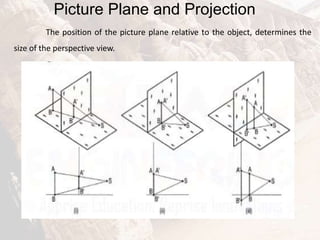
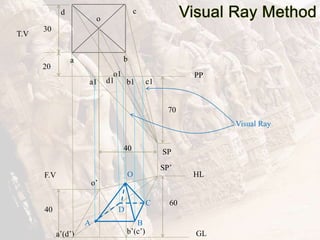
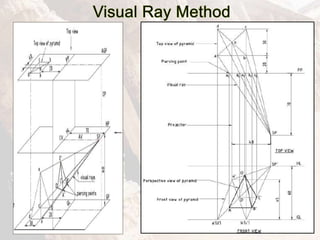
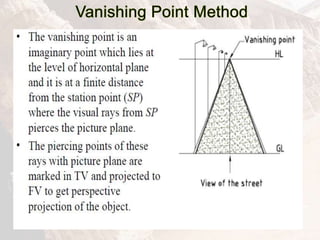
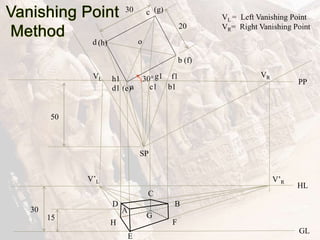
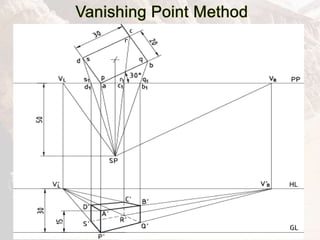
The document provides information on isometric and perspective projections in engineering graphics. It defines isometric projection as a type of pictorial projection that shows the actual sizes of all three dimensions of a solid in a single view. It also defines perspective projection as representing how an object would appear to the eye from a fixed position. The document then discusses principles, scales, views and methods of isometric projection. It provides examples of isometric views of basic geometrical shapes. It also discusses the principles and methods of perspective projection like visual ray and vanishing point methods.

1. 20MEG01
Engineering Graphics
Module V
M. Sundra Pandian, M.E., M.B.A.
Asst. Professor, Department of Mechanical Engineering,
Sri Ramakrishna Institute of Technology,
Coimbatore - 64010

2. Syllabus
Isometricand Perspective Projections (Module 5)
Principles of isometric projection – isometric scale – isometric
projections of simple solids and truncated solids – Prisms, pyramids,
cylinders, cones – Perspective projection of simple solids prisms, pyramids and
cylinder by visual ray method and vanishing point method.

3. Introduction
IsometricDrawing
Isometric projection is a type of pictorial projection in which the three
dimensions of a solid are not only shown in one view, but their actual sizes can
be measured directly from it.

4. Introduction
IsometricProjections
If a cube is placed on one of its corners on the ground with a solid
diagonal perpendicular to the V.P., the front view is the isometric projection of
the cube.

5. Introduction
The three lines CB, CD and CG
meeting at the point C and making 120°
angles with each other are termed isometric
axes.
The lines parallel to these axes are
called isometric lines.
The planes representing the faces
of the cube as well as other planes parallel
to these planes are called isometric planes.

6. Isometric Scale
While drawing this cube the actual sides might get reduced and it is
proportionate the scale called Isometric scale.
It is equal to
2
3
= 0.815
If the true lengths are marked, the
view obtained will be exactly of the same shape
but larger in proportion than that obtained by
the use of the isometric scale
Due to the ease in construction and
the advantage of measuring the dimensions
directly from the drawing, it has
become a general practice to use the true scale
instead of the isometric scale.

7. Isometric View
Let us consider a rectangular prism. The F.V and the T.V will be as
shown

8. Isometric View
The smaller cuboid is drawn according to Isometric scale, that every
dimension is reduced to the isometric scale of  0.8.
The view drawn with isometric scale is called the “Isometric Projection”
and that drawn with original dimension is called “Isometric View or Isometric
Drawing.”
Isometric Projection
Isometric View

9. Isometric Graph
The graph used to draw isometric projections or views is called the
“Isometric Graph”.

10. 30°
Isometric Views of Geometry
The following shows the isometric views of standard geometrical
shapes.
In isometric view, all the sides will be drawn inclined at 30° to the
horizontal.
A B
C
D
30°
90°
a
b
c
d
90°
b
a
c
d
a
30°
30°
b
d
c

11. 30°
Isometric Views of Geometry
The following shows the isometric views of a rectangle.
It is similar to drawing the square but the dimensions b=should be kept
in mind.
A B
C
D
30°
90°
a
b
c
d
90°
b
a
c
d
a
30°
30°
b
d
c

12. 30°
Isometric Views of Geometry
The following shows the isometric views of a triangle.
The position of ‘C’ is measured from either one of the corners ‘3’ or ‘4’
and is transferred to the isometric views.
A B
C
30°
90°
1
2
3
4
90°
2
1
3
4
1
30°
30°
2
4
3
1 2
3
4
a
b
c
a
b
c
a
b
c

13. 30°
Isometric Views of Geometry
The following shows the isometric views of a trapezium.
The position of ‘C’ and ‘D’ are measured from the corners ‘3’ and ‘4’
respectively and is transferred to the isometric views.
A B
C
30°
90°
1
2
3
4
90°
2
1
3
4
1
30°
30°
2
4
3
1 2
3
4
a
b
c
a
b
c
a
b
c
D
d
d
d

14. Isometric Views of Geometry
The following shows the isometric views of a trapezium.
The position of ‘C’ and ‘D’ are measured from the corners ‘3’ and ‘4’
respectively and is transferred to the isometric views.
A B
C
D
1
2
3
4
1
2
3
4
a
b
d
c

15. Isometric Views of Geometry
The following shows the isometric views of a circle.
1. Method of Points
The position of A, C, E and G are marked as the midpoints of the
respective lines , while B, D, F & H are to be measured from both the containing
corners.

16. f
Isometric Views of Geometry
a
b
c
d
e
f
g
h
1 2
3
4
1
2
3
4
c
e
g
b
d
h
a
1. Method of Points

17. Isometric Views of Geometry
1 2
3
4
1
2
3
4
2. Four Center Method
p
q

18. Orthographic to Isometric
Draw the isometric view for the given Orthographic views.

19. Orthographic to Isometric
Draw the isometric view for the given Orthographic views.

20. Orthographic to Isometric
Draw the isometric view for the given Orthographic views.

21. Orthographic to Isometric
Draw the isometric view for the given Orthographic views.

22. Orthographic to Isometric
Draw the isometric view for the given Orthographic views.

23. Orthographic to Isometric
Draw the isometric view for the given Orthographic views.

24. 4’
4
1
Frustum
x y
a
c
d
e
f
b
o
o’
a’ b’ c’ d’
(e’)
(f’)
1’
2’ 3’(5’)
(6’)
1
2 3
4
5
6
p q
r
s
p’ q’
7’ 8’
q’
p’ r’
30°
30°
s’
8’
7’
10’
9’
B
C D
E
F
A
2
3
5
6

25. E
b
a
c
3
2
1
Truncated Solids
Draw the isometric view of a triangular pyramid of base side 30 mm and height 60
mm resting on its base on H.P., such one of its base edge is parallel to V.P. It is cut by a
plane perpendicular to V.P. and inclined at an angle of 45° to H.P. , bisecting the axis.
x y
e f
a’ b’
g’ h’
o
o’
c’
1’
3’
2’
F
C
H
G
I
J
A
O
2
1
B
3
O’

26. H
1’
2’ (8’)
3’ (7’)
4’ (6’) 5’
1
2
8 7
3
5
4
6
Section of Cone
Draw the isometric view of a right circular cone of base diameter 50 mm and height
80 mm resting on its base on h.p. and axis parallel to v.p. it is cut by a plane perpendicular to
v.p. and inclined at an angle of 60° to h.p. at a point on the axis 50 mm above the base
x y
a
b
c
d
e
f
g
h
p q
r
s
a’ e’
o
o’
V
U
W
T
Q
R
P
S
O’
1
O
A C
E
G
F
D
B
Method of Points

27. Section of Cylinder
Draw the isometric view of a frustum cone of base diameter 60 mm and
height 70 mm with a sphere of diameter 40 mm placed centrally above it.
x y
a
b
c
d
e
f
g
h
p q
r
s
a’ e’
o
o’
O’
H O
A C
E
G
F
D
B
Four Centre Method
5’
2’(8’)
1’
3’ (7’)
4’(6’)
P
Q
R
S
O’’
R1 R2
R3
R4
R1 for arc ‘AHG’ R2 for arc ‘CDE’
R3 for arc ‘GFE’ R4 for arc ‘ABC’

28. Perspective View
Perspective projection or perspective drawing is the
representation of an object on a plane surface, called the picture plane,
as it would appear to the eye, when viewed from a fixed position.

29. Perspective View
It may also be defined as the figure formed on the picture plane
when visual rays from the eye to the object cut the picture plane.
Perspective is mainly used in architecture.
By means of perspective, the architect is able to show how an
object would appear when constructed.

30. Perspective View
Ground Plane (GP): It is a horizontal
plane on which the object is assumed
to be situated.
Station Point (S): It is the point where
the eye of the observer is located while
viewing the object.
Picture Plane (PP): It is a vertical
transparent plane located between the
station point and the object which is to
be viewed. It is the plane on which the
perspective is formed.
Horizontal Plane (HP): This imaginary
plane is at the level of the eye, i.e. the
station point. It is a horizontal plane,
above the ground plane and at right
angles to the picture plane.

31. Perspective View
Auxiliary Ground Plane (AGP): It is a
horizontal plane placed above the
horizon plane. The top view of the
object and of the perspective elements
is projected on this plane.
Ground Line (GL): The line of
intersection of the picture plane with
the ground plane is called the ground
line.
Horizon line (HL): It is the line in
which the horizon plane intersects the
picture plane. It is parallel to the
ground line.
Perpendicular axis (PA): It is the line
drawn through the station point,
perpendicular to the picture plane. It is,
sometimes called the Line of sight or
Axis of vision.

32. Perspective View
Centre of vision (C): The point in which
the perpendicular axis pierces the picture
plane is called the centre of vision. It lies
on the horizon line.
Central Plane (CP): It is an imaginary
vertical plane, which passes through the
station point and the centre of vision.
It contains the perpendicular axis. It is
perpendicular to both, the picture plane
and the ground plane.

33. Perspective View

34. Picture Plane and Projection
The position of the picture plane relative to the object, determines the
size of the perspective view.

35. Methods of Perspective View
The two methods of drawing the perspective view
are
1. Visual Ray Method
2. Vanishing Point Method.

36. Visual Ray Method
The two methods of drawing the perspective view
are
1. Visual Ray Method
2. Vanishing Point Method.

37. Draw the perspective view of a square pyramid of base 30 mm side
and height of apex 40 mm rests on GP. The nearest edge of the base is parallel
to and 20 mm behind the picture plane. The station point is situated at a
distance of 70 mm in front of the PP and 40 mm to the right of the axis of the
pyramid and 60 mm above the ground.
• Understand and visualize the reference planes and
object placed on GP.
• Understand and draw the line of intersection of the
planes, object and observer in TV and FV.
• Draw the rays connecting object corners and SP in
TV and FV.
• Draw the visual rays connecting object corners
and SP in TV and FV.
• Mark piercing points of the visual rays in top view
and project and mark them to the corresponding
rays in front view.
• Join the points, draw the visible and hidden edges
to complete the perspective projection of the pyramid.

38. PP
20
T.V
b
c
d
o
30
70
40 SP
a1 b1 c1
d1
o1
GL
40
a
a’(d’) b’(c’)
o’
60
SP’
A B
C
D
O
Visual Ray
F.V HL

41. A rectangular block 30 × 20 × 15 mm is lying on the ground
plane, on one of its largest faces. A vertical edge is in the PP and
the longer edge containing that face makes an angle of 30° with the
picture plane. The station point is 50 mm in front of the picture
plane, 30 mm above the ground plane and lies in the central plane
which passes through the center of the block. Draw the perspective
view of the block by vanishing point method.

42. • Draw TV of the block and rays connecting object corners and SP.
• Draw a line passing through SP and parallel to an inclined edge of
the solid to mark vanishing points.
• Draw the perspective of the edge of the rectangular block which
touches the PP.
• Mark the piercing points of the rays in TV and project them to FV
• Join visible and hidden edges to complete perspective projection.

43. A
a
(e)
PP
30°
20
30
b
c
d
(f)
(g)
(h) o
50
SP
b1
f1
c1
g1
d1
h1
VL
VR
GL
HL
30
V’L V’R
VL = Left Vanishing Point
VR= Right Vanishing Point
E
15
H
D
F
B
G
C