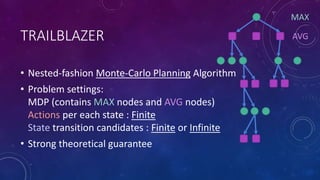
The document presents a paper titled "Blazing the Trails Before Beating the Path: Sample-Efficient Monte-Carlo Planning" which details a nested Monte-Carlo planning algorithm for Markov Decision Processes (MDP). It aims to efficiently estimate the value of states while minimizing calls to a generative model, addressing the trade-off between the number of actions and acceptable estimation error. The paper also discusses theoretical guarantees and the sample complexity performance of the proposed algorithm.

1. BLAZING THE TRAILS BEFORE
BEATING THE PATH:
SAMPLE-EFFICIENT MONTE-
CARLO PLANNING
KATSUKI OHTO
@NIPS2016-YOMI
2017/1/19

2. INTRODUCED PAPER
• Blazing the trails before beating the path:
Sample - efficient Monte-Carlo planning
(JB. Grill, M. Valko and R. Munos)
• NIPS 2016 accepted paper (poster session)
• Abstract starts with “You are a robot…”
• http://papers.nips.cc/paper/6253-blazing-the-trails-before-
beating-the-path-sample-efficient-monte-carlo-planning

3. TRAILBLAZER
• Nested-fashion Monte-Carlo Planning Algorithm
• Problem settings:
MDP (contains MAX nodes and AVG nodes)
Actions per each state : Finite
State transition candidates : Finite or Infinite
• Strong theoretical guarantee
MAX
AVG

4. AIM
• Input : an MDP (Markov Decision Process)
(discount factor 𝛾, maximum number of valid actions 𝐾),
𝜀 (> 0), 𝛿 (0 < 𝛿 < 1)
• Output : estimated value 𝜇 𝜀,𝛿 of current state 𝑠0
• Aim : Get good estimation of real value 𝒱[𝑠0] of current state
such as
ℙ 𝜇 𝜀,𝛿 − 𝒱 𝑠0 > 𝜀 ≤ 𝛿
（ ℙ ∙ means probability of ∙ ）
with the minimum number of calls to the generative model (state transition function)

5. 1 PLAYER TREE MODEL
IN STOCHASTIC ENVIRONMENT
• Each MAX node means an
opportunity to decide action
• Each AVG node means
stochastic state transition
MAX
AVG

6. ALGORITHM OVERVIEW
• Global Initialization
set 𝜂, 𝜆 as global value
set 𝑚 as an argument of
root node
• Recursive algorithm
log(𝜂/𝛾)

7. ALGORITHM OVERVIEW 2
• In both MAX nodes and AVG nodes,
arguments are
𝑚 (desired branching factor)
and
𝜀 (admissible estimation error)
• If 𝑚 is large, we can search many children, but we need much time
(dilemma)
• If 𝜀 is small, we can search deeply, but we need much time (dilemma)

8. ALGORITHM
FOR AVG NODES
• Input : 𝑚 and 𝜀
• Output : estimated value
• If admissible error 𝜀 is large, ignore
successive reward
• Fill 𝑚 transition samples
(and store immediate reward)
• search all of 𝑚 sampled next states
• return averaged immediate reward +
estimated successive reward

9. ALGORITHM
FOR MAX NODES
• Input : 𝑚 and 𝜀
• Output : estimated value
• Fill candidate action pool ℒ by all valid actions
• U is a value like standard error of estimation
• Search candidate actions repeatedly until
“Only 1 action left” or “Error might be small”
• If “Error might be small”
then return estimated value of best action
else
search best action 1 more time carefully

10. SAMPLE COMPLEXITY OF TRAILBLAER
• Sample Complexity is a measure of performance of algorithm
• If N (the number of next states) is finite,
(
1
𝜀
)
max(2,
log 𝑁𝜅
log
1
𝛾
+𝑜 1 )
on condition that 𝜅 ∈ 1, 𝐾 (in detail in
the paper)
else
(
1
𝜀
)2+𝑑
on condition that 𝑑 is a measure of difficulty to identify near-
optimal nodes