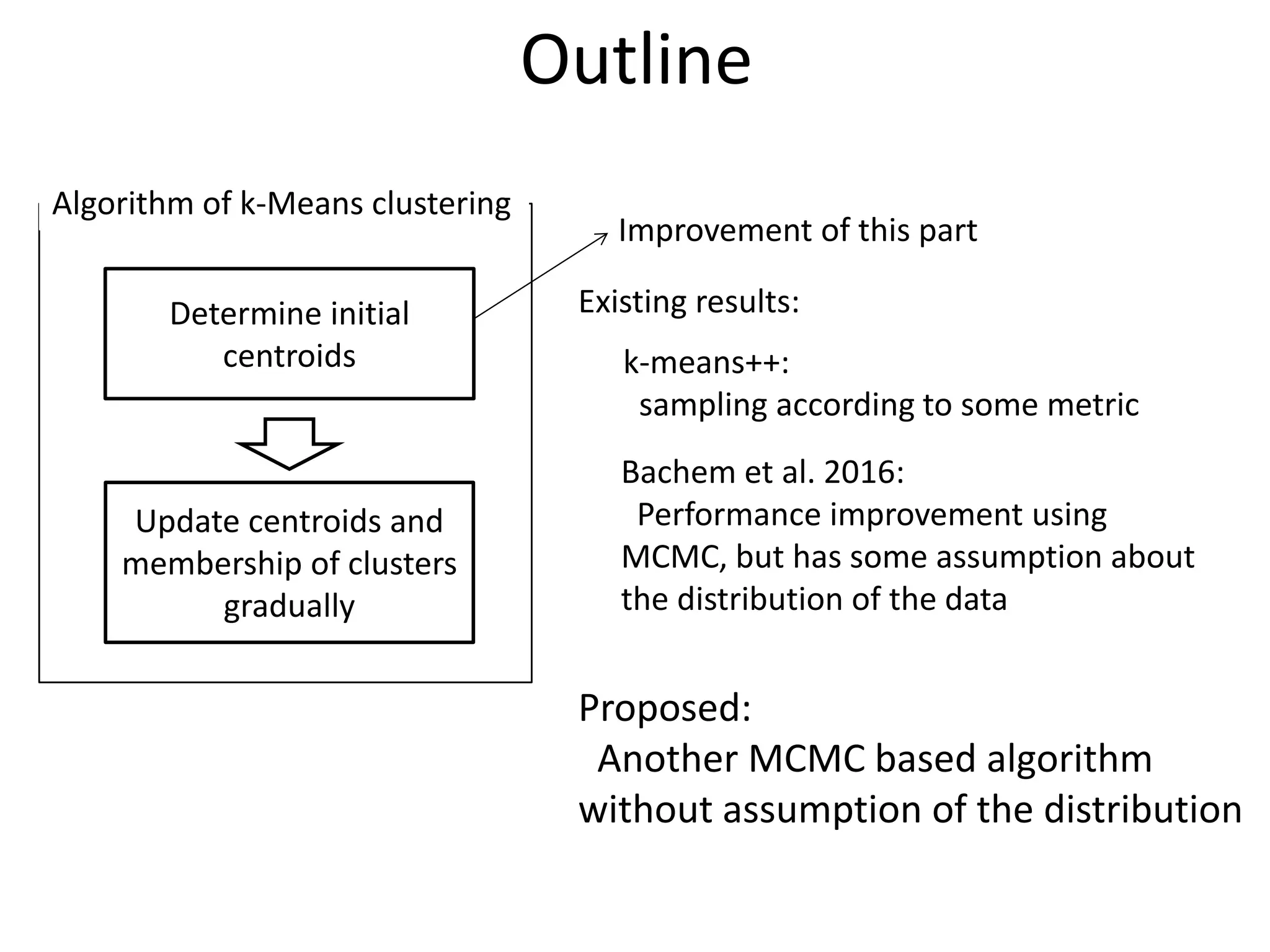
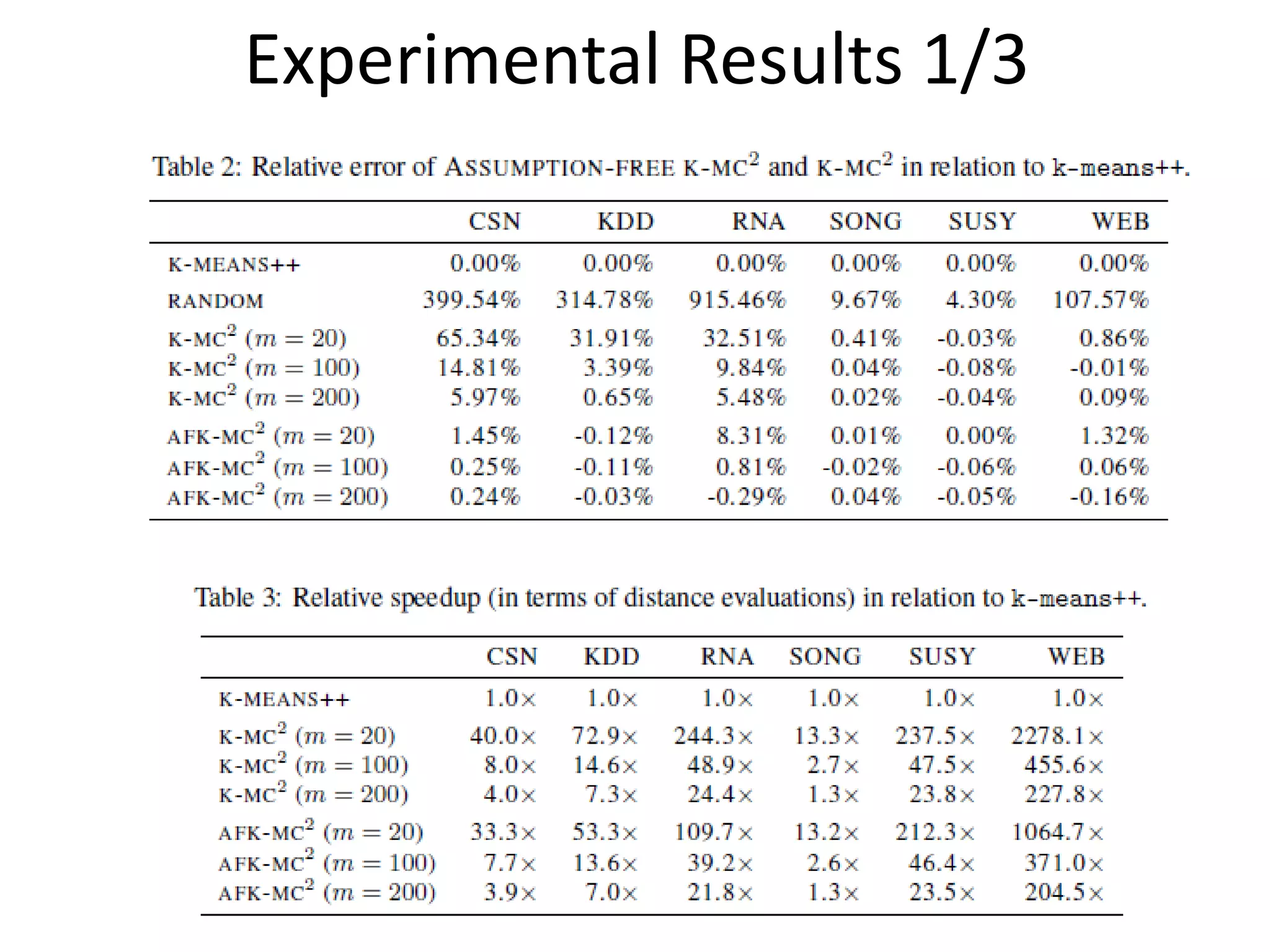
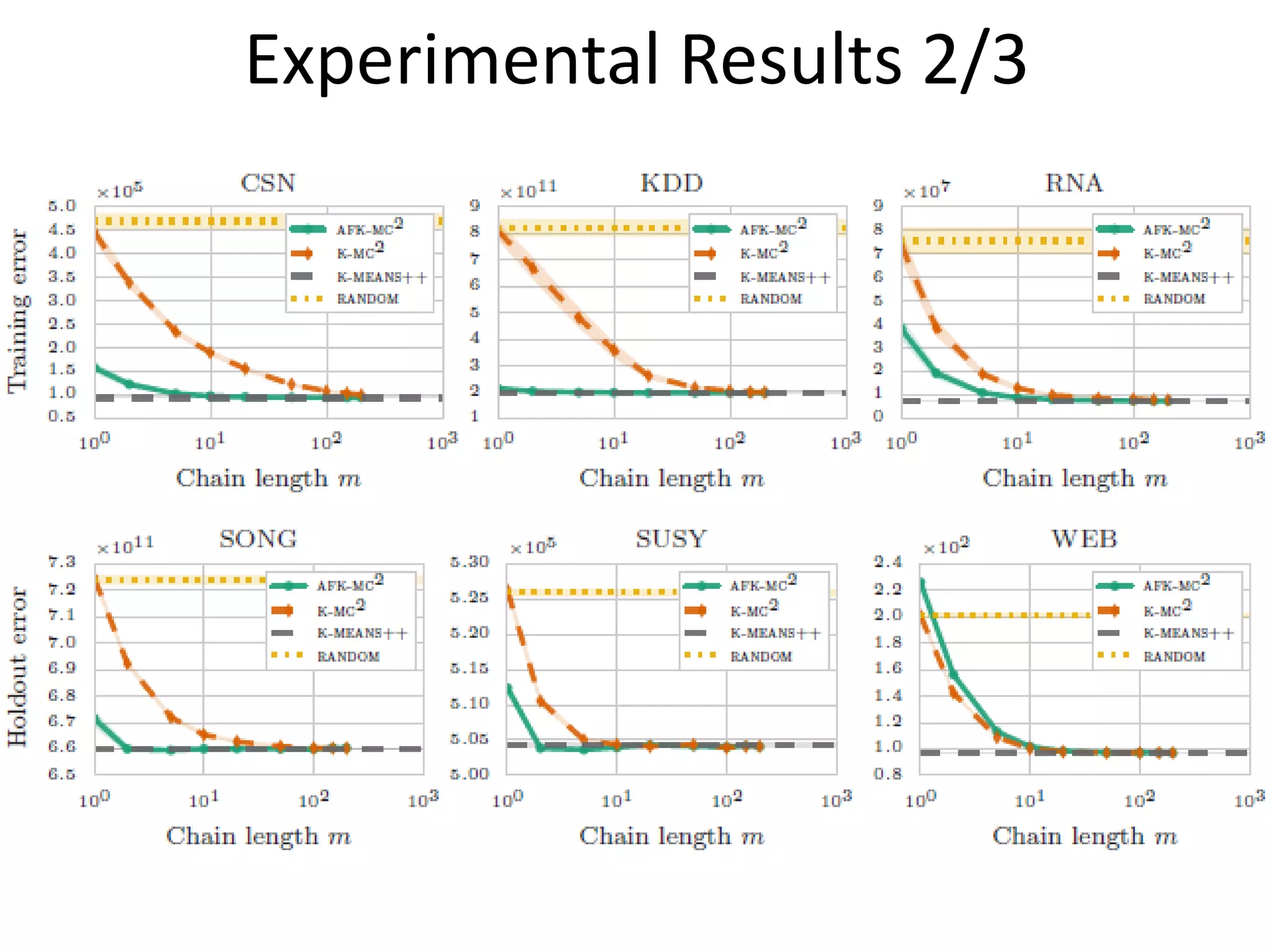
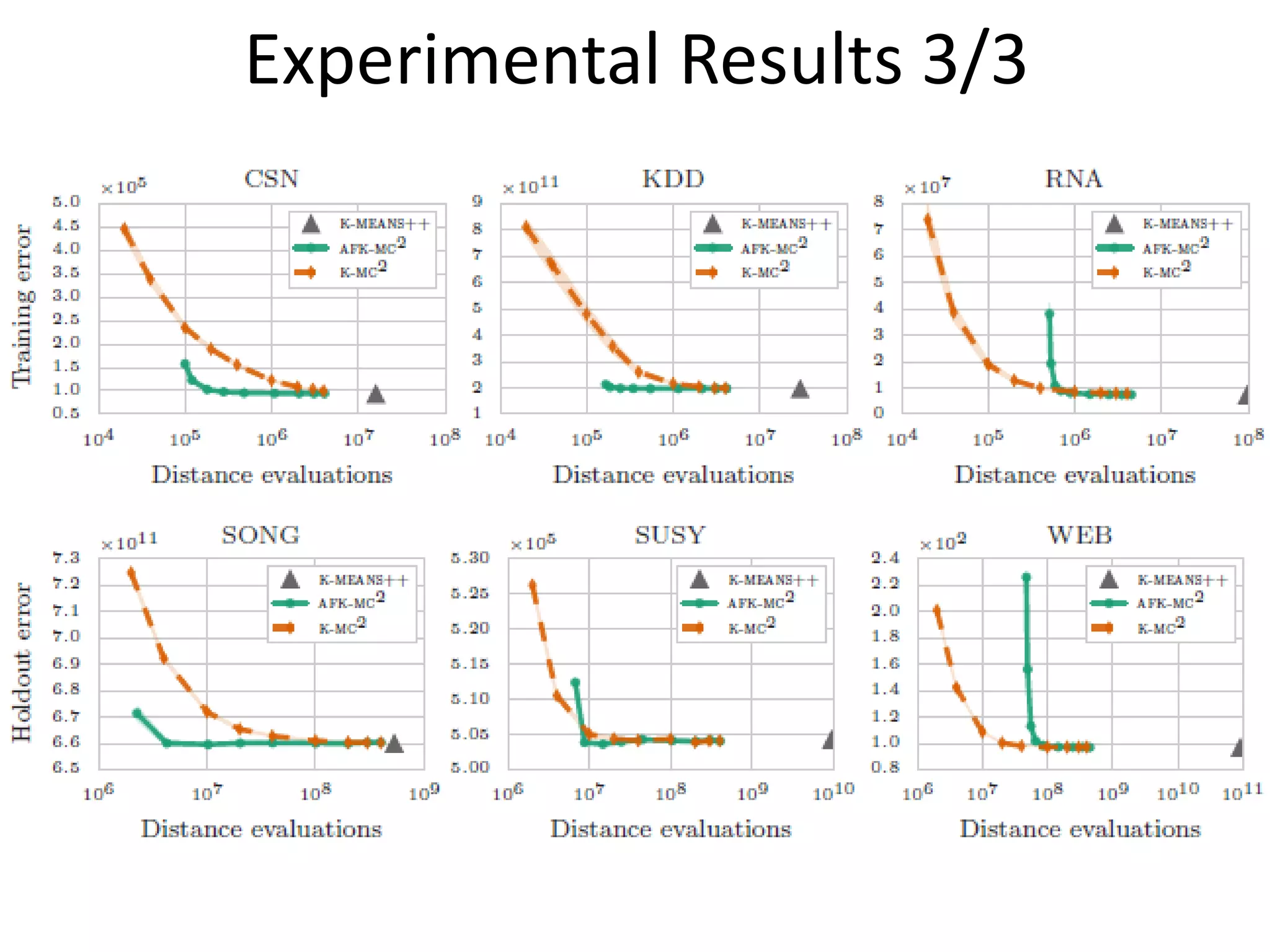
The document proposes a new MCMC-based algorithm for initializing centroids in k-means clustering that does not assume a specific distribution of the input data, unlike previous work. It uses rejection sampling to emulate the distribution and select initial centroids that are widely scattered. The algorithm is proven mathematically to converge. Experimental results on synthetic and real-world datasets show it performs well with a good trade-off of accuracy and speed compared to existing techniques.

1. Fast and Provably Good Seedings for k-Means
O. Bachem, M. Lucic, S. Hassani, A. Krause
Presented by Kimikazu Kato,
Silver Egg Technology Co., Ltd.

2. Algorithm of k-Means clustering
Determine initial
centroids
Update centroids and
membership of clusters
gradually
Improvement of this part
Existing results:
k-means++:
sampling according to some metric
Bachem et al. 2016:
Performance improvement using
MCMC, but has some assumption about
the distribution of the data
Proposed:
Another MCMC based algorithm
without assumption of the distribution
Outline

3. Related researches
kmeans++
Draw
accoding to
Intuition:
Choose initial centroids from the
input data so that they scatter as
widely as possible
Bachem et al. 2016
Intended to overcome the
shortcoming of kmeans++: the
marginalization cost
Metropolitan Hastings algorithm,
which utilizes rejection sampling
to emulate the distribution.
But have some assumption on the
input data.
as a centroid
C: set of centroids which are
already chosen

4. Proposed Algorithm
Update from the preceding result: rejection criterion
The convergence is mathematically proved.

5. Experimental Results 1/3

6. Experimental Results 2/3

7. Experimental Results 3/3

8. Conclusion
• Novel algorithm for the initialization of
centroids in kmeans
• Theoretical guarantee on the convergence
and the trade-off of accuracy and speed
• Experimentally good result