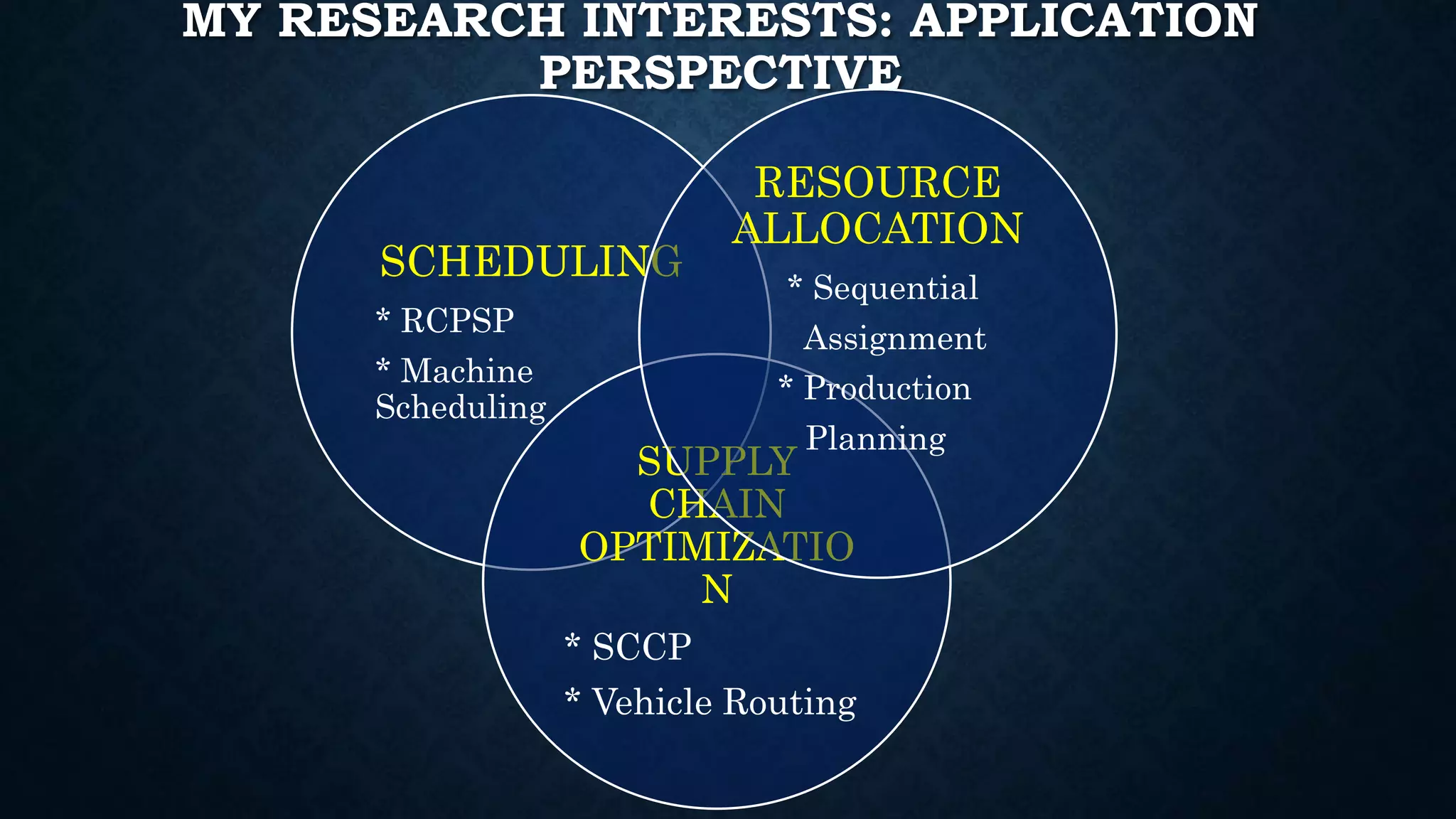
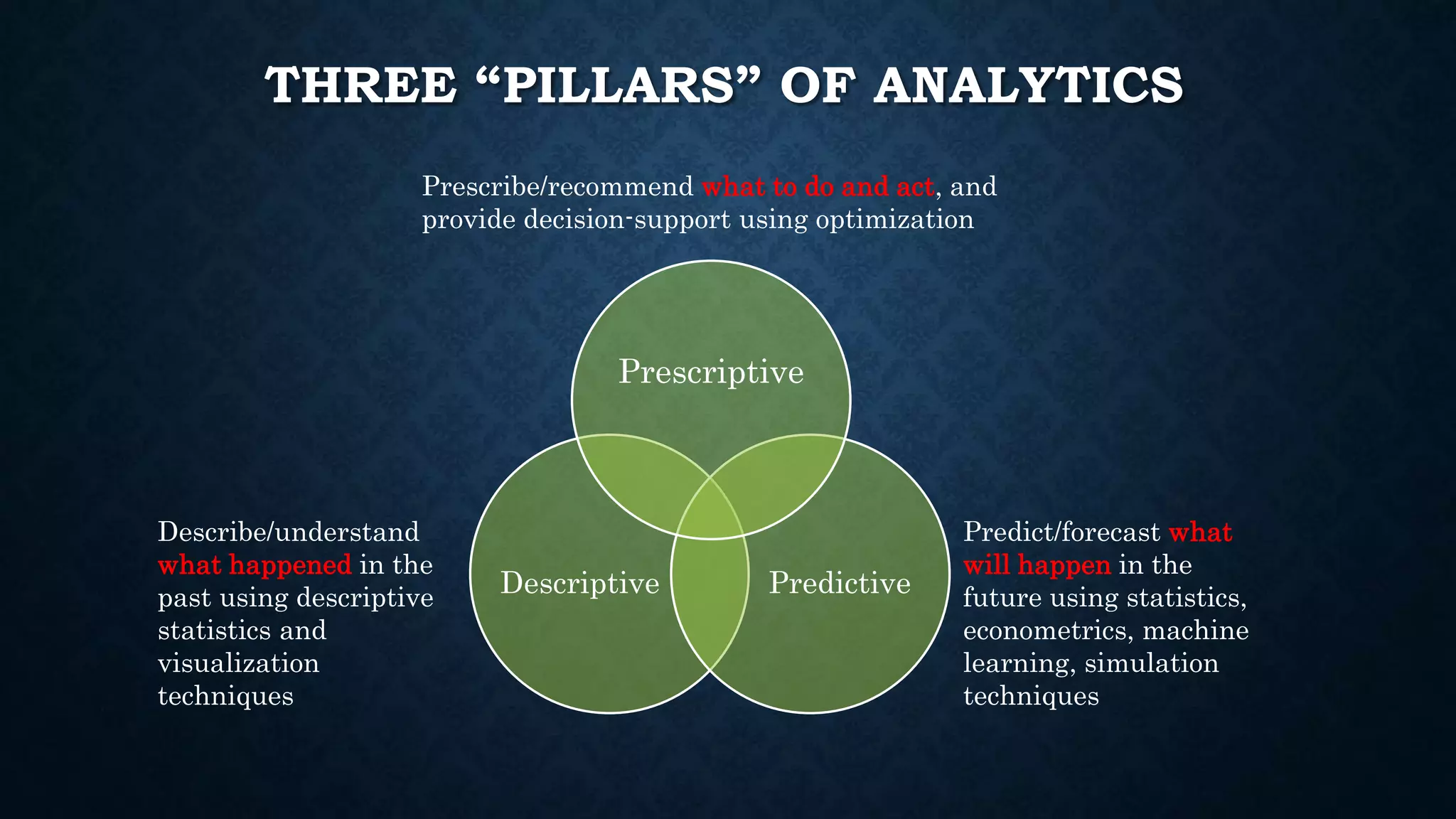
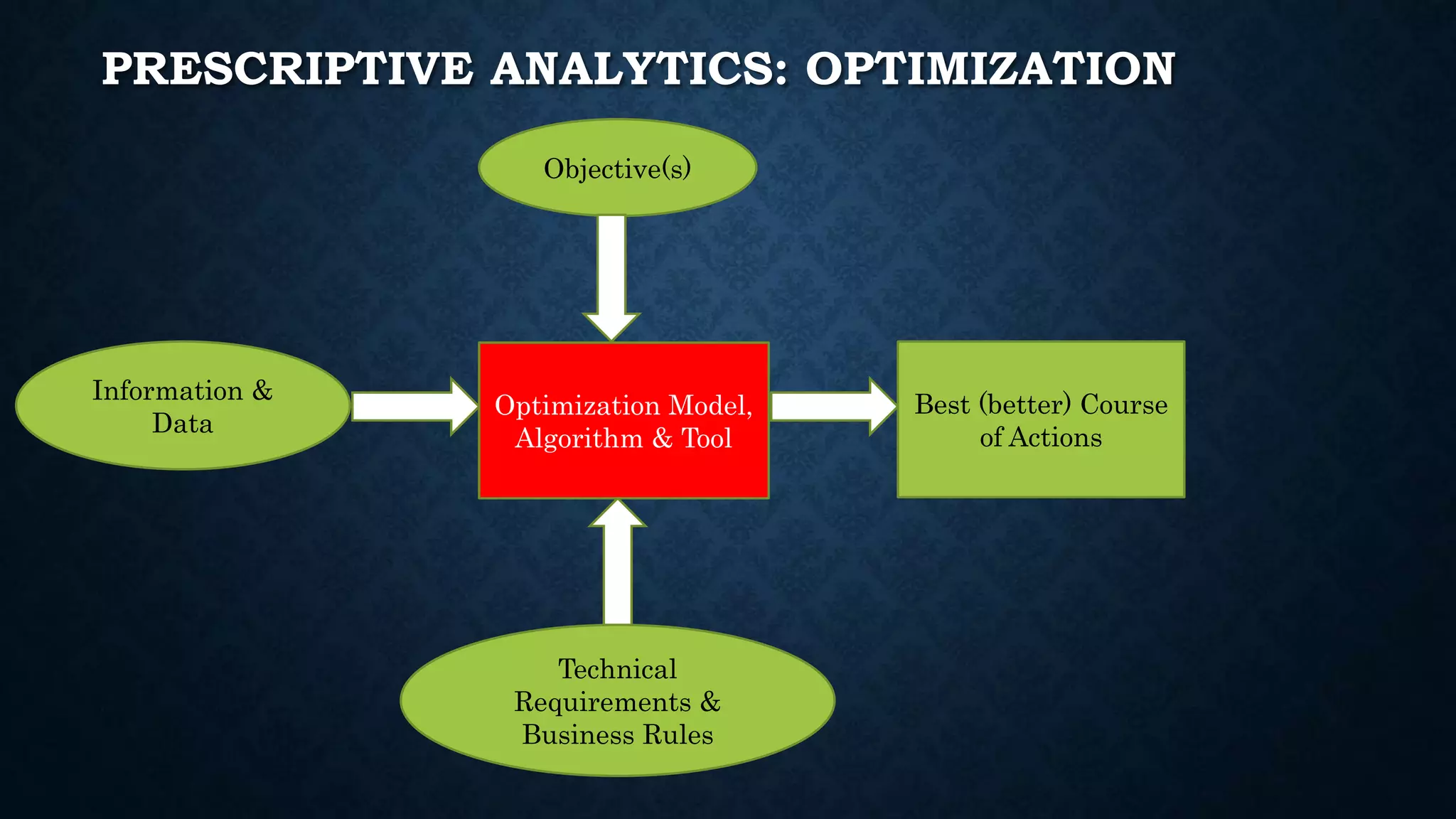
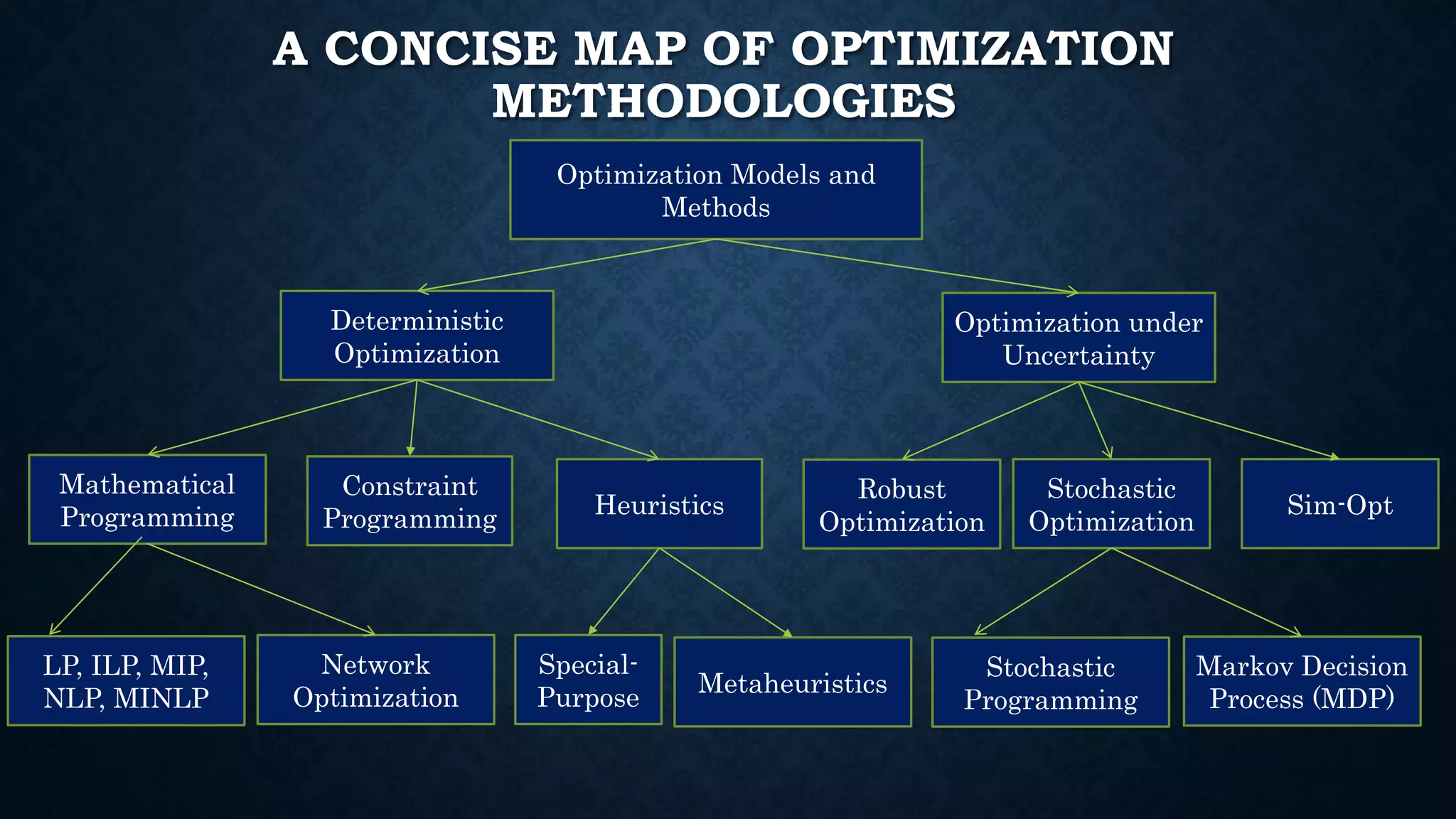
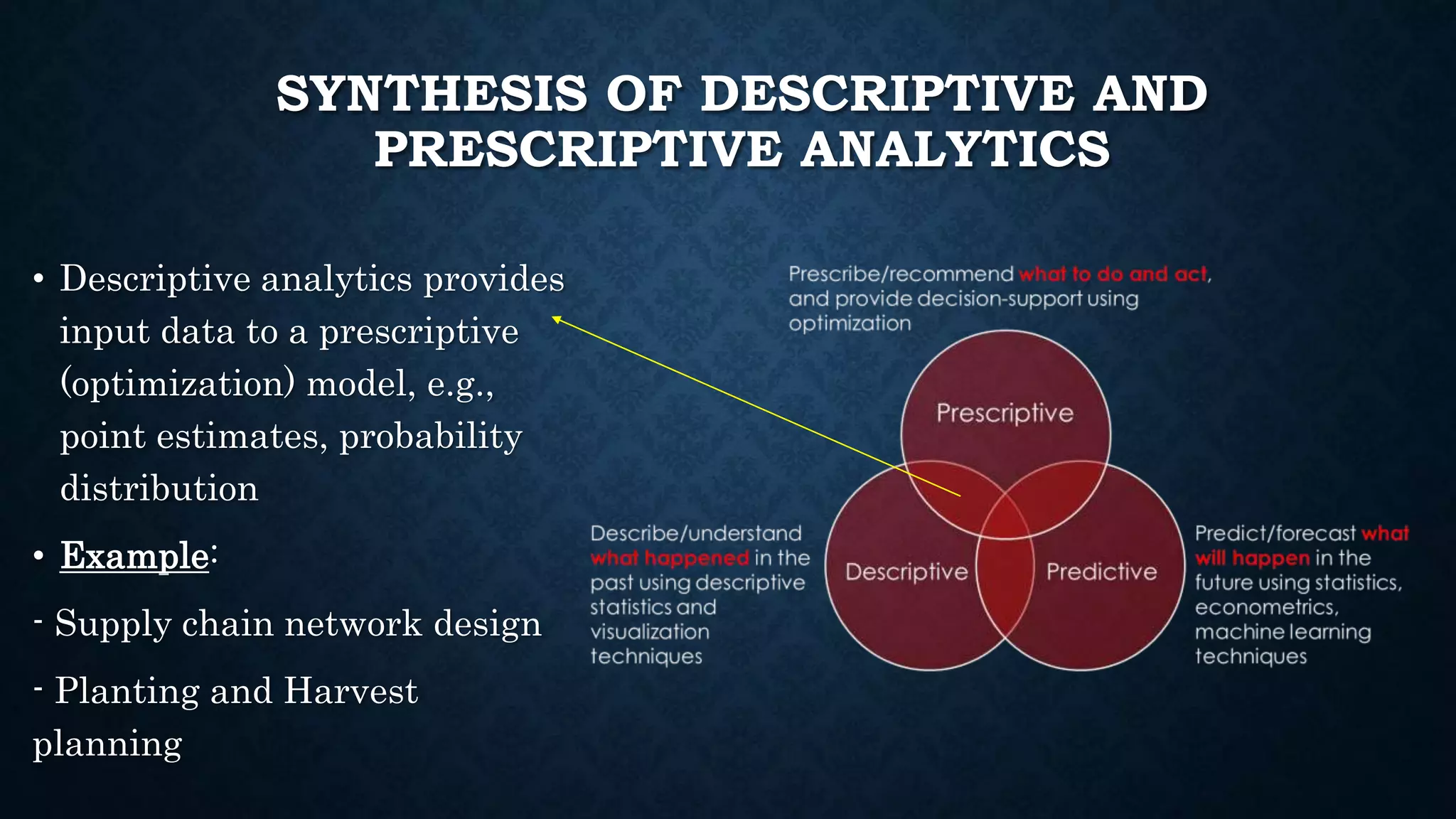
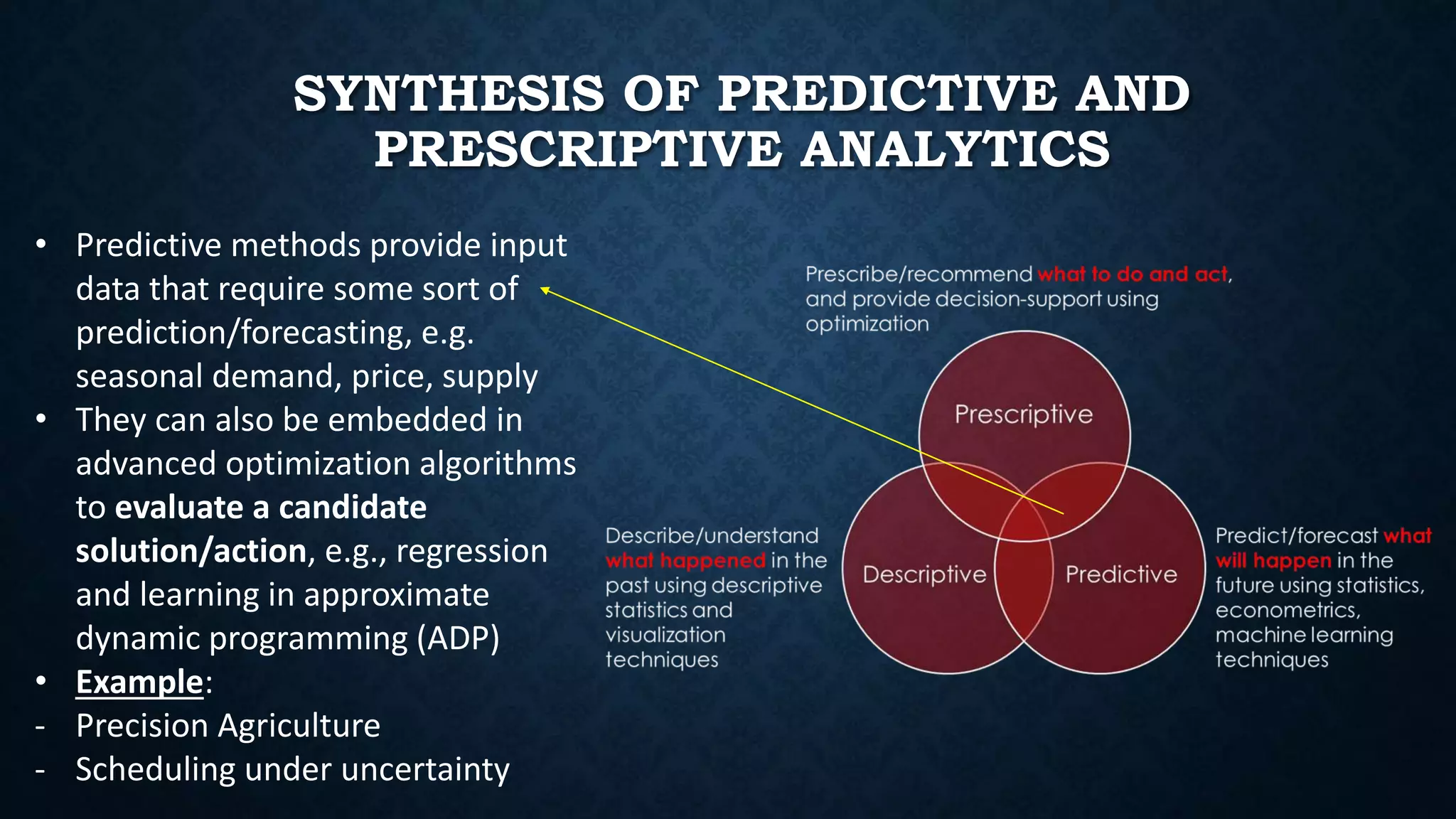
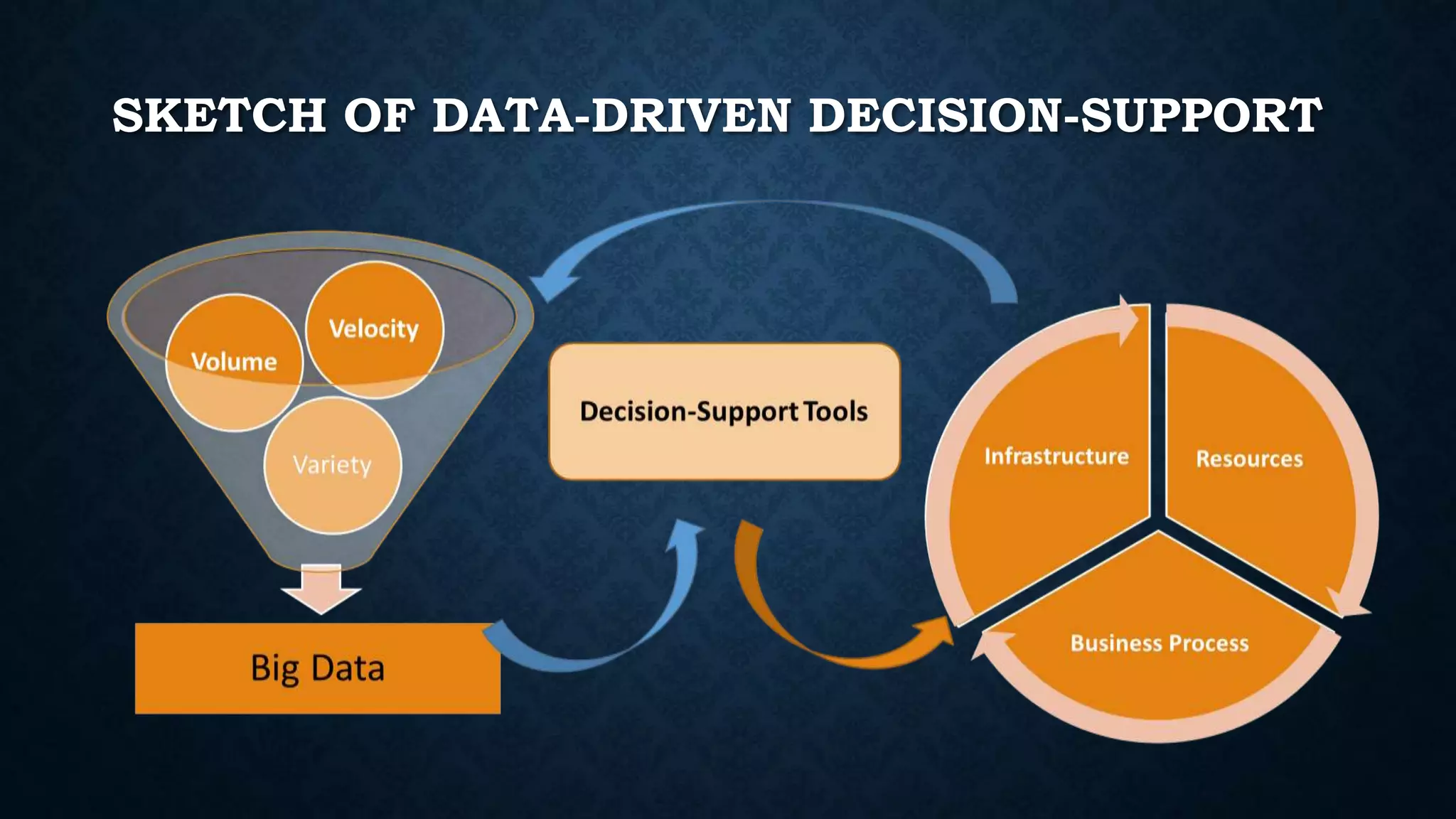
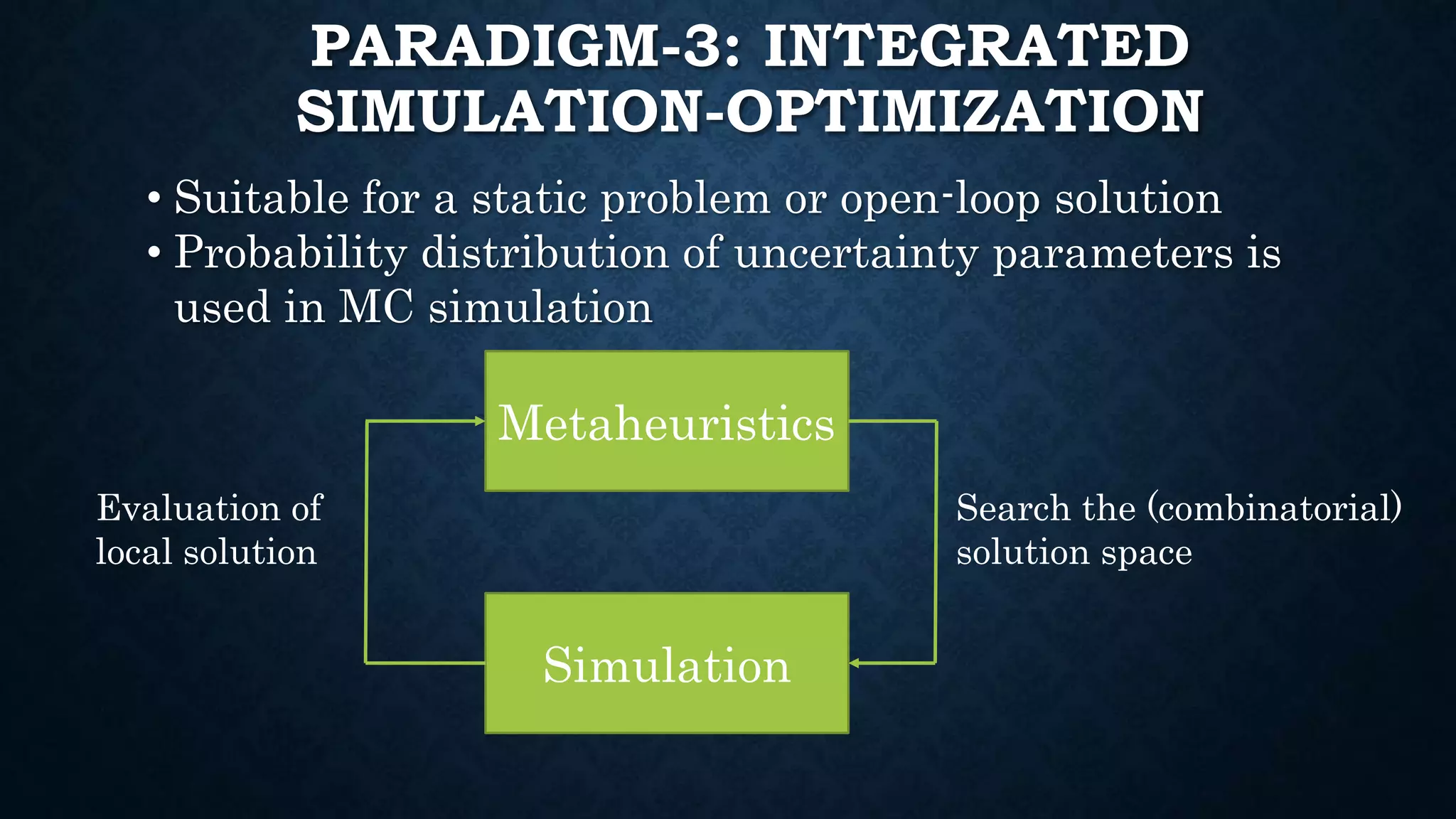
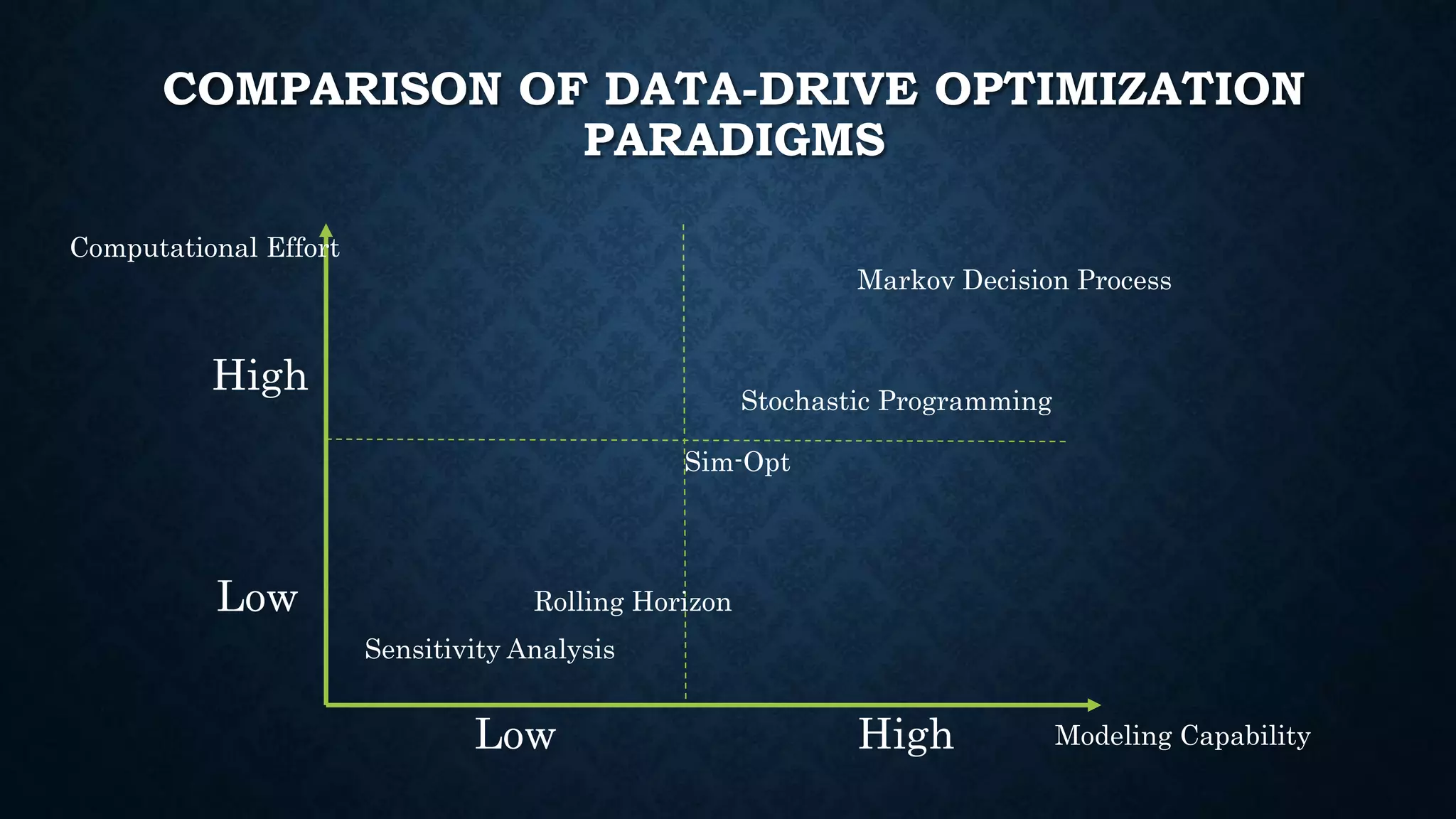
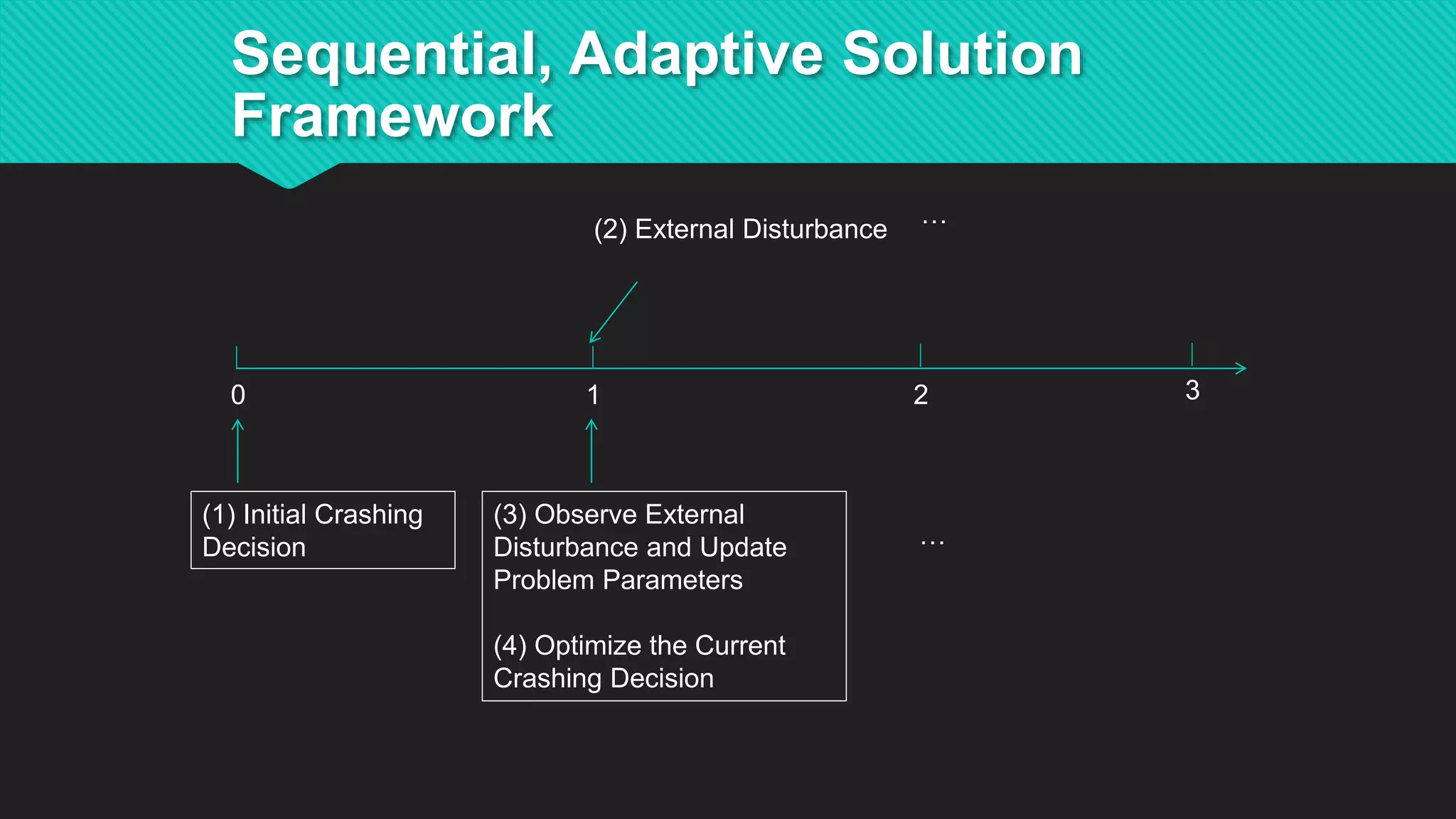
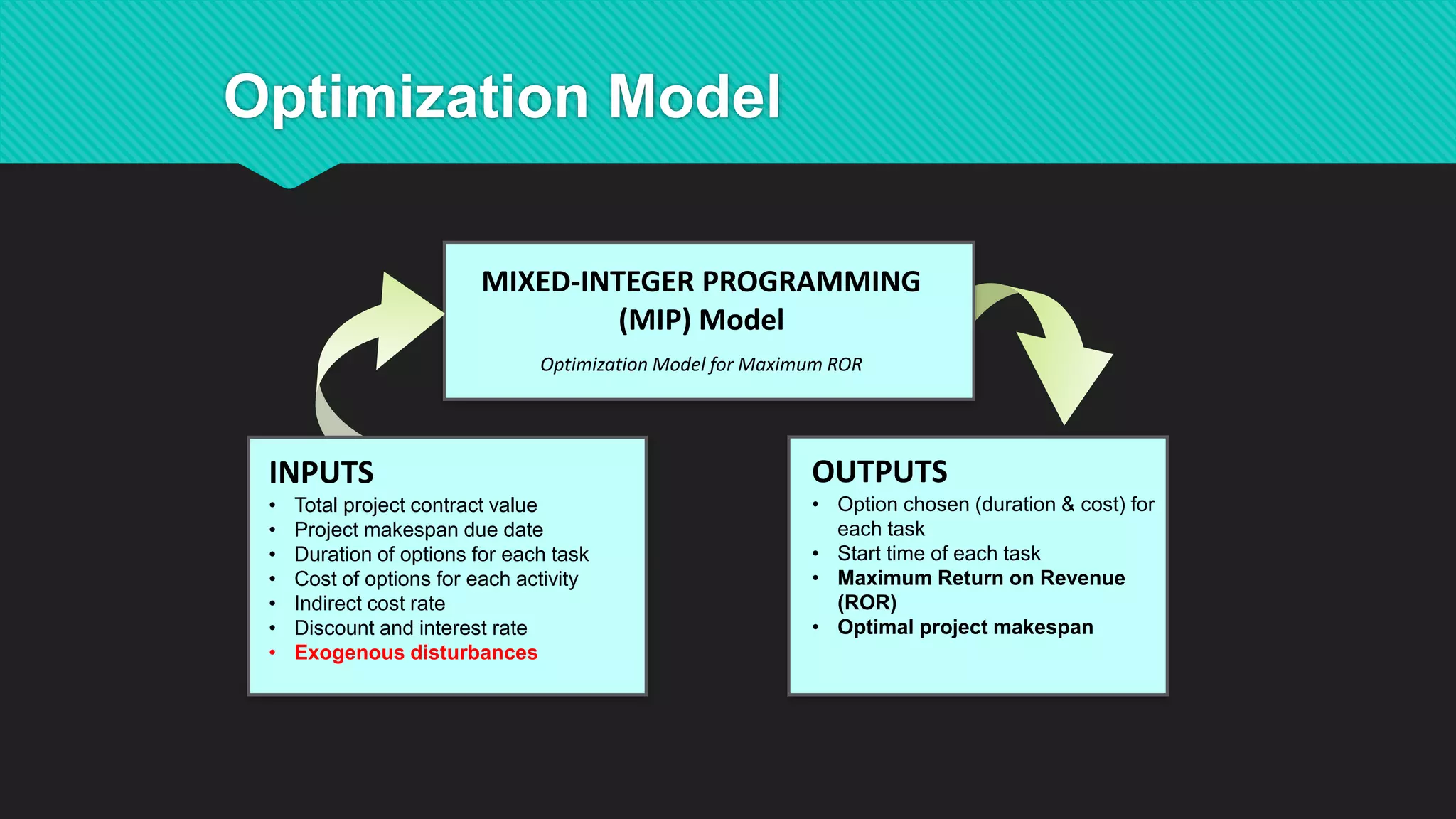
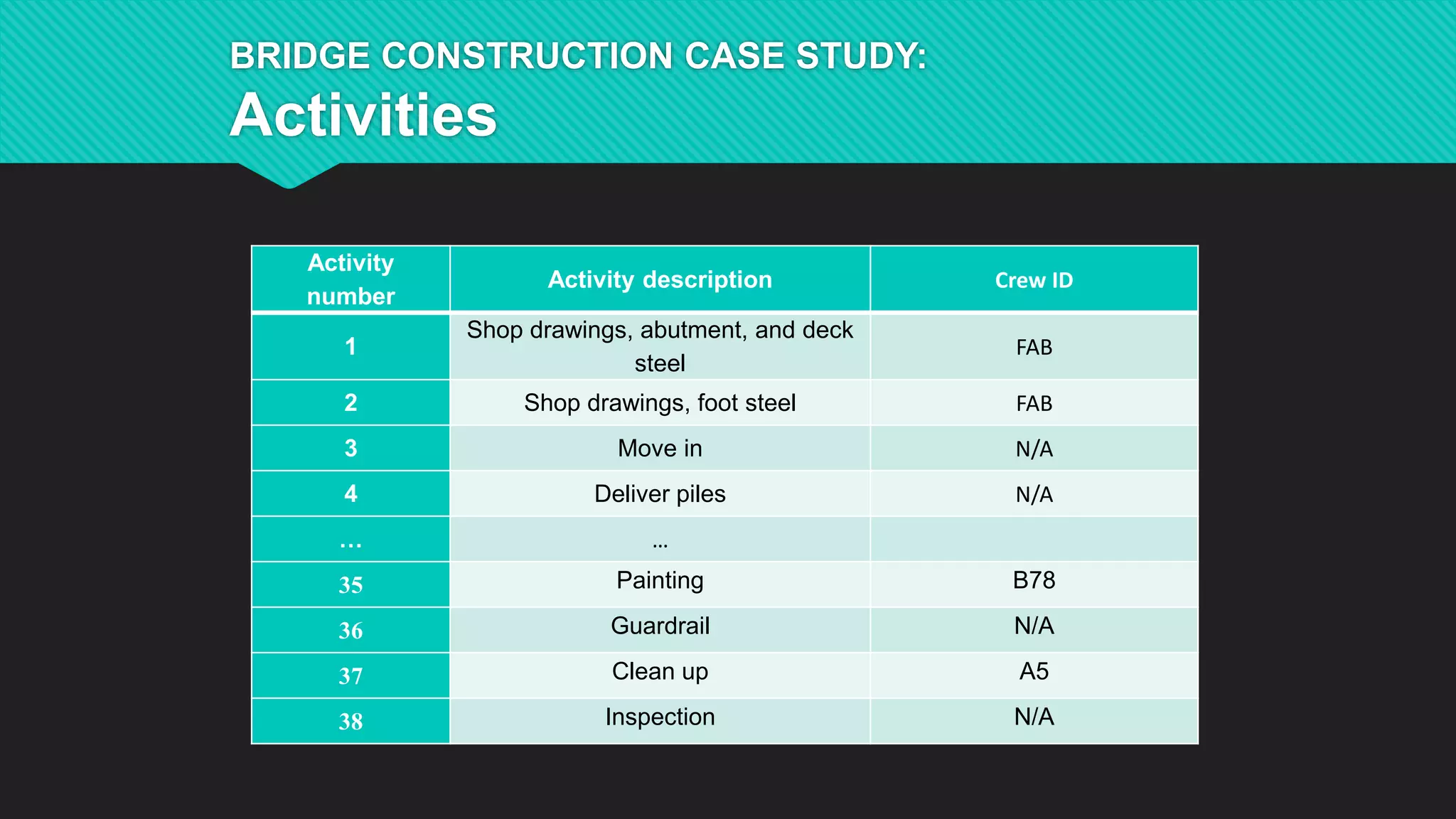
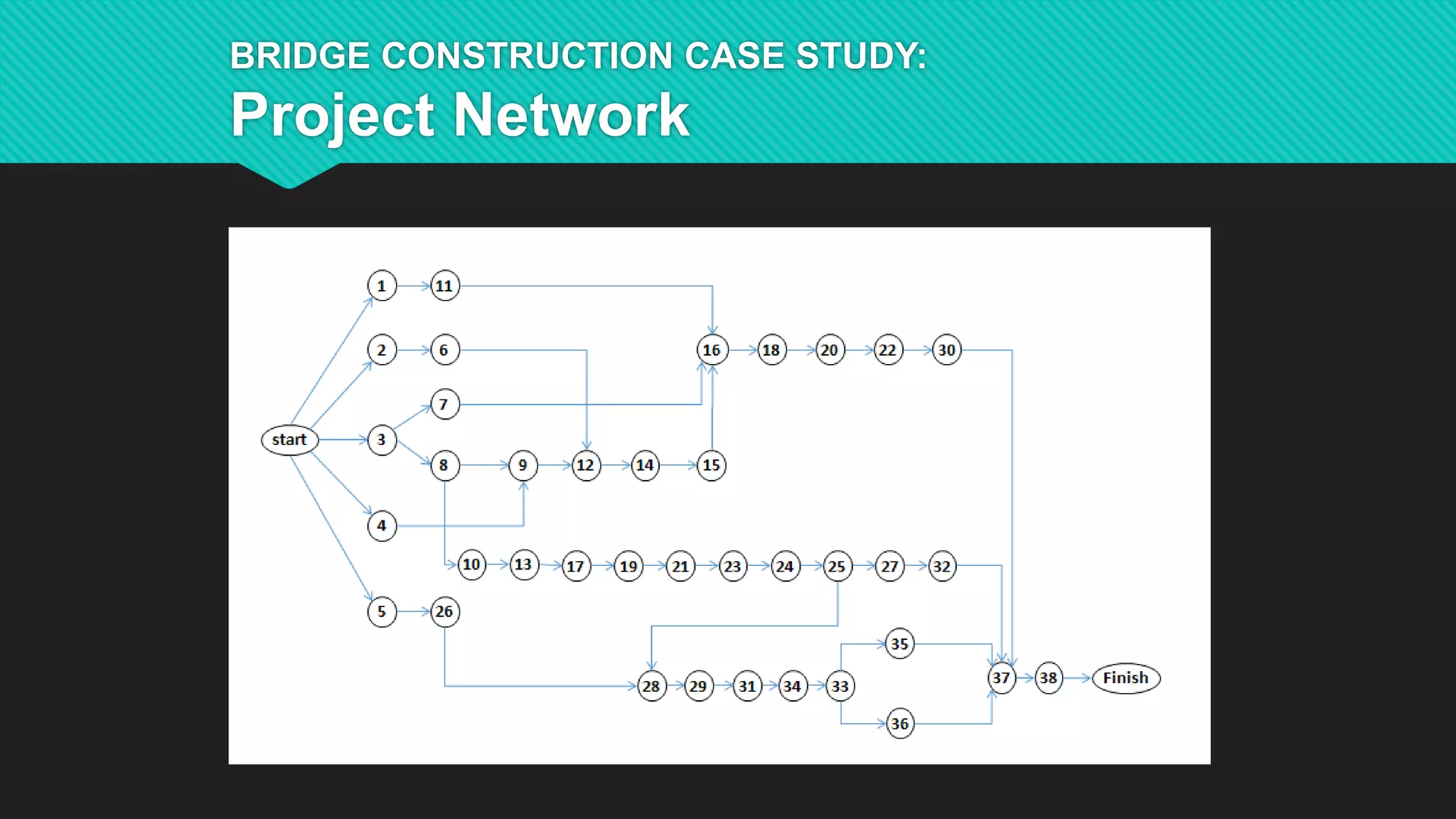
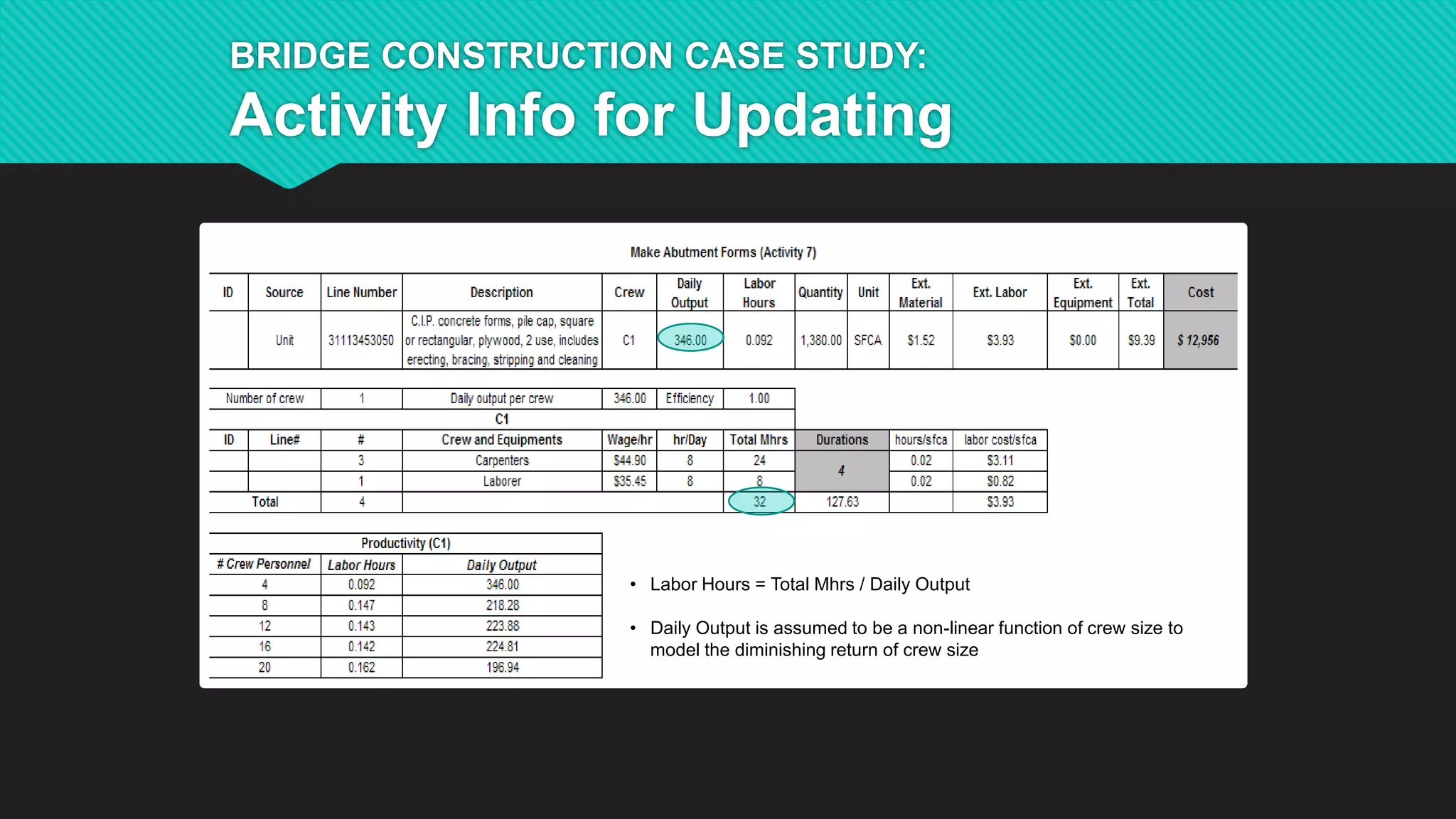
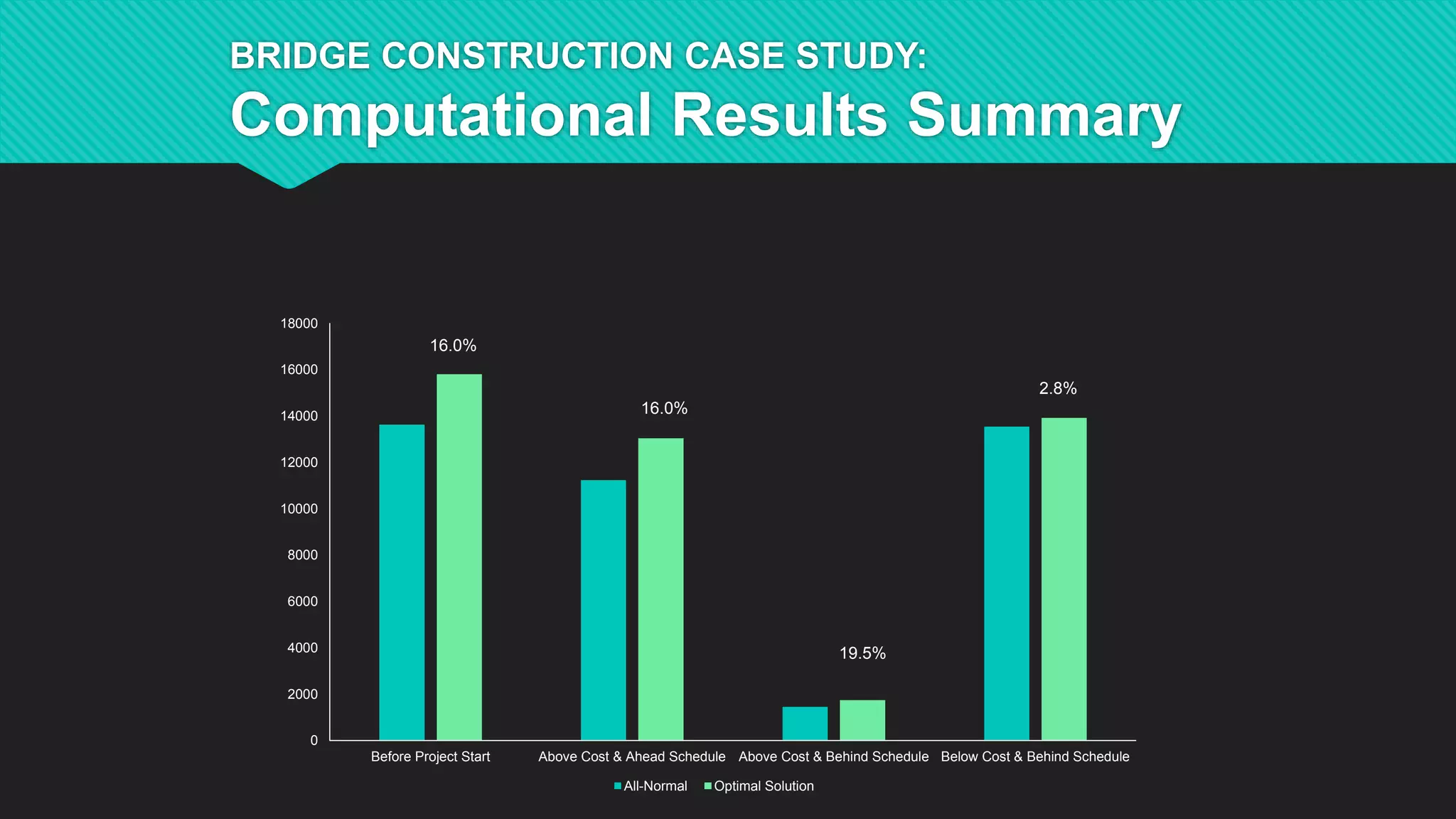
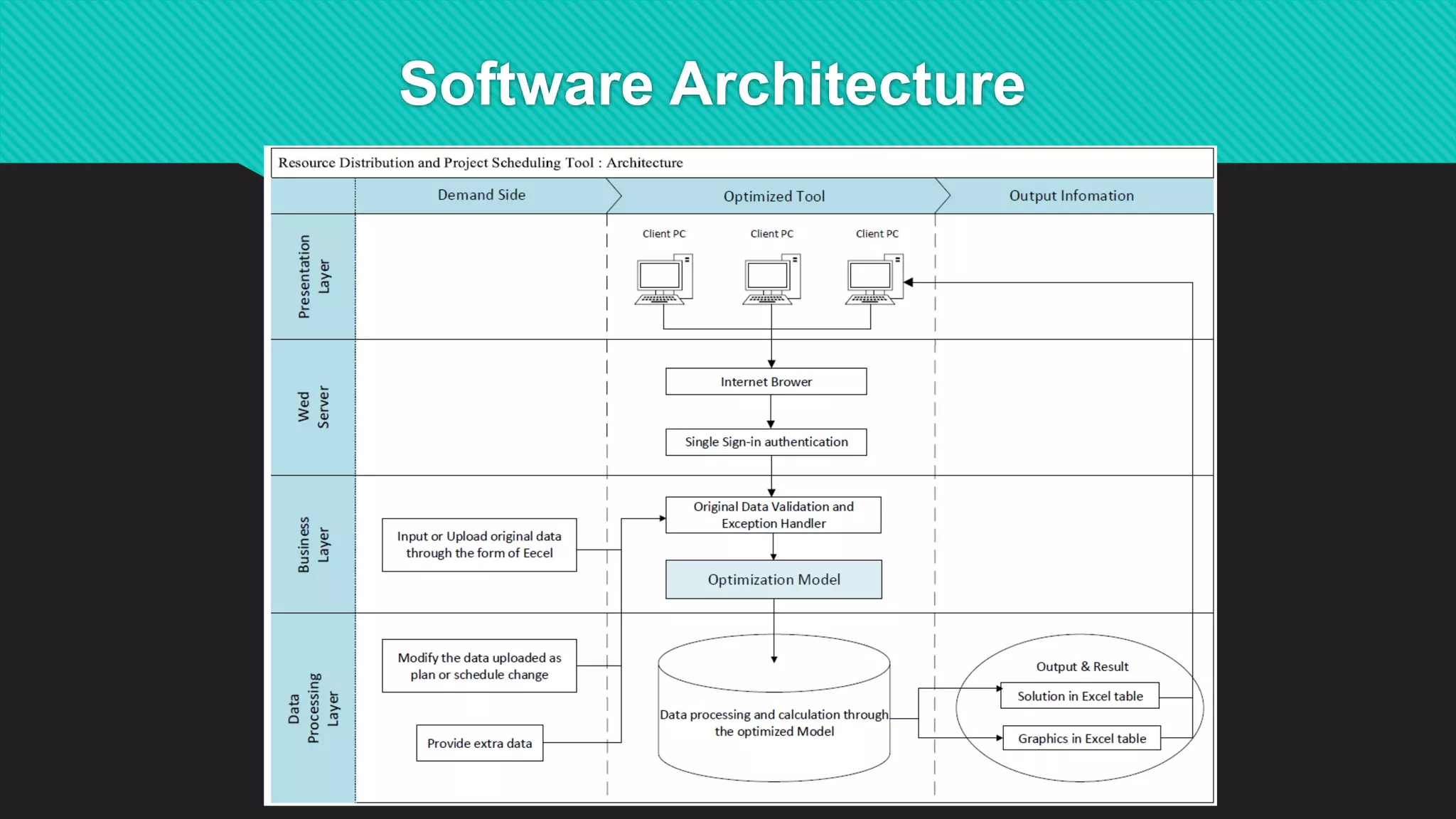
This document summarizes Dr. Haitao Li's presentation on synthesizing analytical methods for data-driven decision making. It discusses the three pillars of analytics - descriptive, predictive, and prescriptive. Various data-driven decision support paradigms are presented, including using descriptive/predictive analytics to determine optimization model inputs, sensitivity analysis, integrated simulation-optimization, and stochastic programming. An application example of a project scheduling and resource allocation tool for complex construction projects is provided, with details on its optimization model and software architecture.