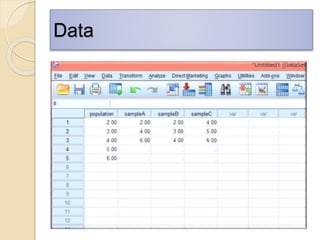
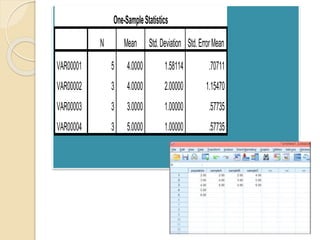
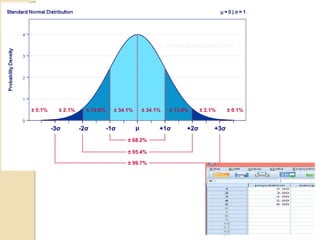
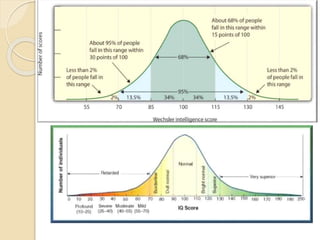
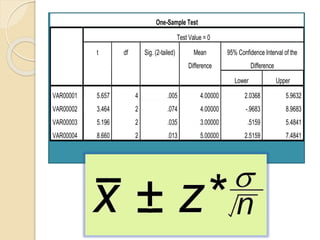
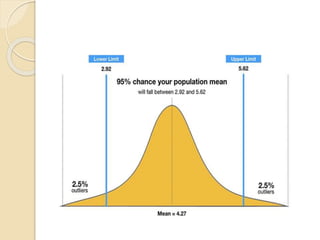
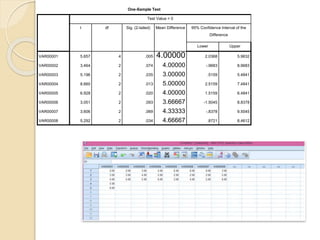
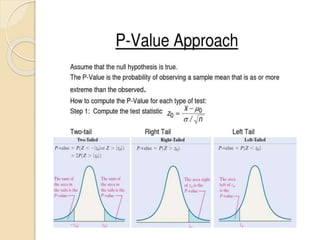
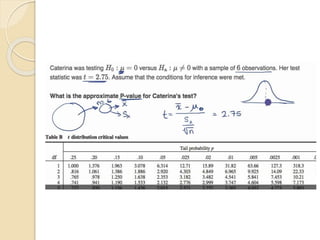
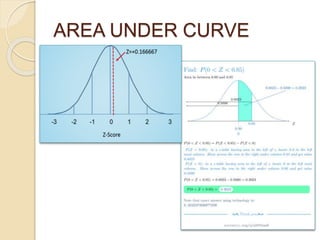
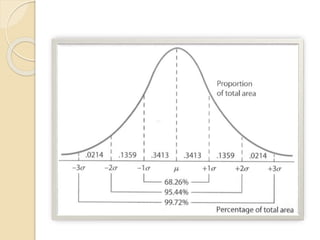
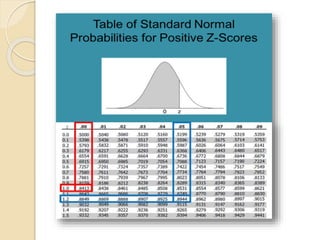
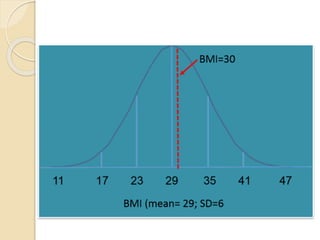
This document discusses statistical concepts like variability, standard deviation, confidence intervals, p-values, and distributions. It provides examples to illustrate variability and how it is important when evaluating investments. It also includes tables showing output from statistical tests run on multiple variables, including sample sizes, means, standard deviations, and confidence intervals. The conclusion emphasizes the relationships between sample size, mean differences, and p-values in determining confidence intervals and statistical significance.

1. INTERPRETATION
OF
STATISTICS
A.THANGAMANI RAMALINGAM
PT, MSc(PSY),PGDRM,ACS
atramalingam@gmail.com

2. Objectives

3. DATA

4. Data

5. “Variability”
 Indicates dispersion, spread, variation, deviation
 For single population or sample data:
where σ2 and s2 = population and sample variance respectively, xi =
individual observations, μ = population mean, = sample mean, and n
= total number of individual observations.
 The square roots are:
standard deviation standard deviation

6. “Variability”
 Why “measure of dispersion” important?
 Consider returns from two categories of shares:
* Shares A (%) = {1.8, 1.9, 2.0, 2.1, 3.6}
* Shares B (%) = {1.0, 1.5, 2.0, 3.0, 3.9}
Mean A = mean B = 2.28%
But, different variability!
Var(A) = 0.557, Var(B) = 1.367
* Would you invest in category A shares or
category B shares?

7. One-SampleStatistics
N Mean Std.Deviation Std.ErrorMean
VAR00001 5 4.0000 1.58114 .70711
VAR00002 3 4.0000 2.00000 1.15470
VAR00003 3 3.0000 1.00000 .57735
VAR00004 3 5.0000 1.00000 .57735

10. CONFIDENCE INTERVAL

11. One-Sample Test
Test Value = 0
t df Sig. (2-tailed) Mean
Difference
95% Confidence Interval of the
Difference
Lower Upper
VAR00001 5.657 4 .005 4.00000 2.0368 5.9632
VAR00002 3.464 2 .074 4.00000 -.9683 8.9683
VAR00003 5.196 2 .035 3.00000 .5159 5.4841
VAR00004 8.660 2 .013 5.00000 2.5159 7.4841

13. P Value

14. One-Sample Test
Test Value = 0
t df Sig. (2-tailed) Mean Difference 95% Confidence Interval of the
Difference
Lower Upper
VAR00001 5.657 4 .005 4.00000 2.0368 5.9632
VAR00002 3.464 2 .074 4.00000 -.9683 8.9683
VAR00003 5.196 2 .035 3.00000 .5159 5.4841
VAR00004 8.660 2 .013 5.00000 2.5159 7.4841
VAR00005 6.928 2 .020 4.00000 1.5159 6.4841
VAR00006 3.051 2 .093 3.66667 -1.5045 8.8378
VAR00007 3.606 2 .069 4.33333 -.8378 9.5045
VAR00008 5.292 2 .034 4.66667 .8721 8.4612

15. TEST STATISTIC

19. AREA UNDER CURVE

23. Take home message
 Frequency data distribution/ sampling
distribution
 Standard normal distribution/ t, z, f
and chi-square distributions
 Large the sample ,narrow the CI
 Large the mean difference, less the p
value.
 Why CI when p less than 0,05