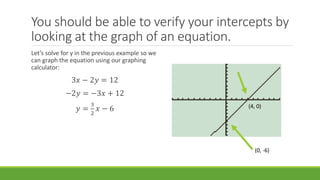
This document explains how to find the x-intercept and y-intercept of a graph from its equation. The x-intercept is where the graph crosses the x-axis and is of the form (x,0), while the y-intercept is where the graph crosses the y-axis and is of the form (0,y). To find the x-intercept, set y=0 and solve for x; to find the y-intercept, set x=0 and solve for y. Examples are provided finding the intercepts of equations by setting variables equal to 0 and solving.

1. Intercepts
HOW TO FIND THEM USING EQUATIONS AND GRAPHS

2. An intercept is where a graph crosses an
axis.
An x-intercept is where a
graph crosses the x-axis.
A y-intercept is where a
graph crosses the y-axis.

3. Properties of Intercepts
An x-intercept is always of the form (x, 0), because
the y-coordinate must be 0 for the point to sit on the
x-axis.
A y-intercept is always of the form (0, y), because the
x-coordinate must be 0 for the point to sit on the y-
axis.

4. To find intercepts from an equation:
To find the x-intercept of an equation, set y = 0
and solve for x.
For example, let’s find the x-intercept of the
graph of 3x – 2y = 12.
-Plug in 0 for y: 3x – 2(0) = 12
-Solve for x: 3x – 0 = 12
3x = 12
x = 4
The x-intercept is located at (4, 0).
To find the y-intercept of an equation, set x = 0
and solve for y.
For example, let’s find the y-intercept of the
graph of 3x – 2y = 12.
-Plug in 0 for x: 3(0) – 2y = 12
-Solve for x: 0 – 2y = 12
-2y = 12
y = -6
The y-intercept is located at (0, -6).

5. You should be able to verify your intercepts by
looking at the graph of an equation.
Let’s solve for y in the previous example so we
can graph the equation using our graphing
calculator:
3𝑥 − 2𝑦 = 12
−2𝑦 = −3𝑥 + 12
𝑦 =
3
2
𝑥 − 6
(0, -6)
(4, 0)

6. Find the intercepts of 4y = 2x – 6.
Let’s find the x-intercept first by plugging in 0
for y:
4(0) = 2x – 6
0 = 2x – 6
6 = 2x
3 = x
The x-intercept is (3, 0).
Let’s find the y-intercept next by plugging in 0
for x:
4y = 2(0) – 6
4y = 0 – 6
4y = -6
y = -1.5
The y-intercept is (0, -1.5)