The document is a revision guide for engineering mathematics, specifically focusing on integration techniques, derivatives, trigonometric identities, and their applications. It discusses various integration methods such as substitution, integration by parts, and the importance of familiarity with derivative rules and trigonometric identities. Additionally, it emphasizes the flexibility of choosing appropriate techniques according to individual understanding and problem requirements.

1. KIX 1001
Engineering Mathematics 1
Dr. KHOO SHIN YEE
Office: Level 6, Engineering Tower
Department: Mechanical Engineering
Email: khooshinyee@um.edu.my
Week 8– Integration
(An Introduction)
Part 7: Summary & Revision
Reference: James, G., Burley, D., Clements, D.,
Dyke, P., & Searl, J. (2015). Modern engineering
mathematics. Pearson Education.

2. Overall Remarks
• Remember the basic derivative & integral functions as well as the
trigonometric identities & rule (e.g. quotient rule etc.)
• Understand the integration techniques such as the integration by
part; substitution & trigonometric substitution; partial fraction
with factoring, completing the square; etc.
• There is no way to teach which technique is the best as that
usually depends upon the person and which technique they find
to be the easiest.
• It’s entirely possible that you will need to use more than one
method to completely do an integral. For instance a substitution
may lead to using integration by parts or partial fractions integral
or involves identities, factoring, etc.
• In my class, I will accept any valid integration technique as a
solution.
2
Note: These points are more greared towards my class and it’s completely possible
that your instructor may not agree with this, so be careful in applying this point if you
aren’t in my class
© 2019 Dr Khoo Shin Yee

3. Revision - Basic Derivative Rule
(i) For polynomial function
(ii) For Rational Function (Hint: quotient rule )
(iii) For exponential function (Hint: with base ??)
(iv) For composite function (Hint: product rule/ composite function rule)
3
( sin ) = (sin )+sin ( ) = cos +sin
d d d
x x x x x x x x x
dx dx dx
3 (3-1) 2
( ) = 3 = 3
d
x x x
dx
3 3
3 2 3 2
2 2 2
(2 +1) ( )- (2 +1) (2 +1)(3 )-2 (4 +3)
( ) = = =
2 +1 (2 +1) (2 +1) (2 +1)
d d
x x x x
d x x x x x x
dx dx
dx x x x x
2
-
( ) =
du dv
v u
d u dx dx
dx v v
(5 ) = 5 (ln5)
x x
d
dx
( ) = (ln ) =
x x x
d
e e e e
dx
Base 5>>
Base e>>
2 2 2 2-1 2 2
, ( ) '( ( ))
'( )
, ( ( ))
( 5 +6 ) = 2(5 +6 ) . (5 +6 ) = 2(5 +6 )(5+12 )
inner function g x f g x
g x
outer function f g x
d d
x x x x x x x x x
dx dx
© 2019 Dr Khoo Shin Yee

4. Revision - Basic Derivative Rule
(v) For inverse function (Hint: Inverse rule ; ff-1(x)=x)
e.g. y=sin-1x; x=siny; dx/dy=cosy=sqrt(1-sin2y)=sqrt(1-x2)
(vi) For trigonometric Function (Hint: quotient rule)
Hint: Remember the derivative for sin, tan, sec, the rest can be obtained by the
following relationships: +ve >> -ve; sin >> cos; tan>>cot; sec>>csc
4
-1
2
1
(sin ) =
1-
d
x
dx x
1
=
/
dy
dx dx dy
-1
2
1
(tan ) =
+1
d
x
dx x
-1
2
1
(sec ) =
( -1)
d
x
dx x x
-1 -1
(cos ) = - (sin )
d d
x x
dx dx
-1 -1
(cot ) = - (tan )
d d
x x
dx dx
-1 -1
(csc ) = - (sec )
d d
x x
dx dx
1
(ln ) =
d
x
dx x
(sin ) = cos
d
x x
dx
2
(tan ) = sec
d
x x
dx
(sec ) = sec tan
d
x x x
dx
(cos ) = -sin
d
x x
dx
2
(cot ) = -csc
d
x x
dx
(csc ) = -csc cot
d
x x x
dx
2
2
2
(ln +1) = =
+1
d x derivative of denominator
x
dx x denominator
© 2019 Dr Khoo Shin Yee

5. 5
Revision– Trigonometric Identities
• Trigonometric identities
• Angle sum and differences identities
• Product to sum identities • Double angle identities
Hypotenuse
=𝑟
𝑨𝒅𝒋𝒂𝒄𝒆𝒏𝒕
= 𝑟cosθ
Opposite=
𝑟𝑠𝑖𝑛θ
sin( )
tan( ) = =
cos( )
Opposite
Adja
θ
cent
θ
θ
1
sec( ) =
cos( )
x
x
1
cot( ) =
tan( )
x
x
1
cosec( ) =
sin( )
x
x
sin( ) =
Opposite
Hypo
θ
tenuse
cos( ) =
Adjacent
Hypo
θ
tenuse
reciprocal
2 2 2
2 2
+ =
sin +cos =1
Opposite Adjacent Hypotenuse
θ θ
2 2
tan +1= sec
θ θ
2 2
cot -1= csc
θ θ
2
÷cos θ
2
÷sin θ
+ = sin co
) o
( s + c s
sin α β α β αsinβ
cos + = cos cos -sin
( )
α β α β αsinβ
- = -
( ) ;
sin β sinβ
cos( )
- = cos
β β
- = sin co
) o
( s -c s
sin α β α β αsinβ
cos - = cos cos +sin
( )
α β α β αsinβ
(
1
sin cos = + -
2
) + ( )
α β sin α β sin α β
(
1
cos cos = [cos ) +
+ cos - )
2
( ]
α β α β α β
(
1
sin sin = [cos ) -
- cos + )
2
( ]
α β α β α β
sin(2 ) = 2sin cos
x x x
2 2 2 2
cos(2 ) = cos -sin = 2cos -1=1-2sin
x x x x x
© 2019 Dr Khoo Shin Yee

6. 6
Revision– Trigonometric Identity (Appendix)

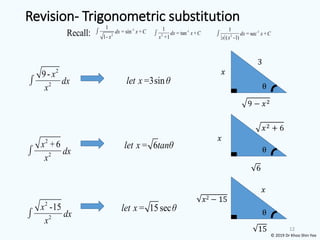
7. Revision- Basic Integration Rule
(i) For polynomial function
(ii) For Rational Function (Hint: substitution; partial fraction; long
division; trigonometric substitution)
(iii) For exponential function (Hint: with base ??)
(iv) For composite function (Hint: Substitution; Integration by part)
7
1
( ) = ln +
dx x C
x
= + = +
ln
x
x x
e
e dx C e C
e
Integration as Antiderivative
(2+1)
2 3
3
3 = + = +
(2+1)
x
x dx C x C
(-2+1)
2
1 1
( ) = + = - +
(-2+1)
x
dx C C
x x
2
2
2
( ) = ln +4 +
+4
x
dx x C
x
5
5 = +
ln5
x
x
dx C
2 2 2
t /
2(5 +6 )(5+12 ) = (5 +6 ) +
dt dx
x x x dx x x C
( cos +sin ) =[ sin - sin ]+[-cos ]+ = sin +
u dv u v v du
x x x dx x x xdx x C x x C
-1
2
1
= sin +
1-
dx x C
x
-1
2
1
= tan +
+1
dx x C
x
-1
2
1
= sec +
( -1)
dx x C
x x
Integration as Antiderivative
or trigonometric substitution
© 2019 Dr Khoo Shin Yee

8. Revision- Basic Integration Rule
(i) For inverse function (Hint: Inverse rule )
e.g. y=sin-1x=f-1(x); x=siny=f(y); Ans=xsin-1x-∫sinydy=xsin-1x+cosy=xsin-1x+sqrt(1-x2)
(vi) For trigonometric Function (Hint: substitution)
Hint: Remember the derivative for sin, tan, sec, the rest can be obtained by the
following relationships: +ve >> -ve; sin >> cos; tan>>cot; sec>>csc
8
-1 -1 2
(sin ) = sin + 1- +
x dx x x x C
(ln ) = ln - +
x dx x x x C
(sin ) = -cos +
x dx x C
-1
2 1
( ) = - ( )
total
area area
area
f x dx xy f y dy
-1 -1 2
1
(tan ) = tan - ln +1 +
2
x dx x x x C
(cos ) = sin +
x dx x C
(tan ) = -ln cos +
x dx x C (cot ) = ln sin +
x dx x C
(sec ) = ln sec + tan +
x dx x x C (csc ) = -ln csc +cot +
x dx x x C
Integration as Antiderivative
(sec tan ) = sec +
x x dx x C
2
(sec ) = sec +
x dx x C 2
(csc ) = -csc +
x dx x C
(csc cot ) = -csc +
x x dx x C
© 2019 Dr Khoo Shin Yee

9. Revision- Basic Integration Rule (Appendix)
9
𝑁𝑜𝑡𝑒: 𝑎 > 0
Important formula that
you need to master

10. • How to select “u” & “dv” in integration by parts
• Convention/ Common practice:
Select “u” for function easier to differentiate (i.e. inverse function such as ln|x|
& sin-1x)
Select “dv” function easier to integrate (i.e. e^x)
• Rule of thumb:
1. Logarithm
2. Inverse trigonometric function
3. Algebraic function
4. Trigonometric function
5. Exponential function
10
Tendency to
choose u
(difficult to
integrate)
Revision- Integration by part
© 2019 Dr Khoo Shin Yee
Example:
‫׬‬ 𝑥 ln 𝑥 𝑑𝑥 = ‫׬‬ 𝑢 𝑑𝑣 = 𝑢𝑣 − ‫׬‬ 𝑣 𝑑𝑢
𝐿𝑒𝑡 𝑢 = 𝑙𝑛𝑥 𝐿𝑒𝑡 𝑑𝑣 = 𝑥𝑑𝑥
𝑑𝑢 = 𝑑𝑥/𝑥 𝑣 = ‫׬‬ 𝑥 𝑑𝑥=x2/2
2 2
ln = ln - +
2 4
x x
x xdx x C

11. More examples that can use substitution method
11
2 5
sin cos
x xdx
2 6
tan sec
x xdx
Substitution
Let sin x=t ;
dt/dx=cosx
2 2
sin +cos =1
trigonometry identity
x x
2 2
sec -tan =1
trigonometry identity
x x Substitution
Let tan x=t ;
dt/dx=sec2x
2
+1
+2 +2
x
dx
x x
Substitution
Let x2+2x+2=t ;
dt/dx=2x+2=2(x+1)
= ln +
,
derivative of D
dx D C
denominator D
1
2+ 1-
dx
x
Substitution
Let sqrt(1-x)=t ;
dt/dx=-
𝟏
𝟐𝒕
= ln +
,
derivative of D
dx D C
denominator D
2
1-
x x dx
Substitution
Let sqrt(1-x2)=t ;
dt/dx= −
𝒙
𝒕
2
1- x dx Normal Substitution
sqrt(1-x2)=t
Is not working
Required
Trigonometric
Substitution
8 2
1-
x x dx
7 2
1-
x x x dx Substitution
Let sqrt(1-x2)=t ; dt/dx= −
𝒙
𝒕
;
x=sqrt(1-t2)
© 2019 Dr Khoo Shin Yee
Substitution
Let t=1-x ;
dt/dx= −𝟏

12. 12
2
2
9- x
dx
x
=3sin
let x θ
θ
9 − 𝑥2
𝑥
3
2
2
+6
x
dx
x
θ
𝑥2 + 6
𝑥
6
= 6
let x tanθ
2
2
-15
x
dx
x
θ
𝑥2 − 15
𝑥
15
= 15sec
let x θ
Revision- Trigonometric substitution
-1
2
1
= sin +
1-
dx x C
x
-1
2
1
= tan +
+1
dx x C
x
-1
2
1
= sec +
( -1)
dx x C
x x
Recall:
© 2019 Dr Khoo Shin Yee

13. Revision: Converting improper func. >> proper
• By using long division
13
3
+
= ?
-1 proper
improper
x x
x 3 2
( -1)
+0 + +0
x
x x x
2
x
3 2
-
x x
−
2
+
x x
+x
2
-
x x
−
2x (𝑅𝑒𝑚𝑎𝑖𝑛𝑑𝑒𝑟)
3
2
+ 2
= + +
-1 -1
improper
improper
x x x
x x
x x
• Try
2
2
4 -3 +2
= ?
4 -4 +3 proper
improper
x x
x x
2
2 2
(4 -4 +3)
4 +0 -3 +2
x x
x x x
1
2 2
4 +0 -4 +3
x x x
−
-1
x
(𝑅𝑒𝑚𝑎𝑖𝑛𝑑𝑒𝑟)
2
2 2
4 -3 +2 -1
=1+
4 -4 +3 4 -4 +3
improper proper
x x x
x x x x
© 2019 Dr Khoo Shin Yee
2
2x
− 2 -2
x
2 (𝑅𝑒𝑚𝑎𝑖𝑛𝑑𝑒𝑟)
-1
x
3
2
+ 2
= + +2+
-1 -1
proper
improper
x x
x x
x x

14. Revision: Factorization
(for polynomial function of degree 4 and above)
• Factorize the 𝑥4 − 5𝑥2 + 4
• ∴ 𝑥 − 1 (𝑥 + 1)(𝑥 − 2)(𝑥 + 2)
• Factorize the 4𝑥4 + 4𝑥3 − 3𝑥2 − 4𝑥 − 1
• ∴ 𝑥 − 1 2𝑥 + 1 2 𝑥 + 1
• Factorize the 𝑥4 + 2𝑥3 + 𝑥2 − 4
• ∴ 𝑥 − 1 𝑥2 + 𝑥 + 2 𝑥 + 2
• Factorize the 𝑥4 + 2𝑥3 + 5𝑥2 + 4𝑥 + 4
• ∴ 𝑥2 + 𝑥 + 2 2
14
>>Distinct linear factor
>>repeated linear factor
>>distinct quadratic factor
>>repeated quadratic factor
© 2019 Dr Khoo Shin Yee

15. Revision: Completing the square
15
• Formula:
• Example:
2x2
− 12x-9
Step 1: Factoring = 2(x2−6x)-9
Step 2: Apply formula
2 2 2
+ + = ( + ) -( ) +
2 2
b b
ax bx c a x c
a a
= 2[(x −
6
2
)2 −
6
2
2
] − 9)
= 2(x − 3)2
−2(9) − 9)
= 2(x − 3)2 −27
© 2019 Dr Khoo Shin Yee

16. 16
Case Factor in
denominator
Term in partial fraction decomposition
1 Linear factor
2 Linear factor (repeated)
3 Quadratic factor
& irreducible
4 Quadratic factor
(repeated)
& irreducible
𝑎𝑥 + 𝑏
𝑎𝑥 + 𝑏 k
𝑎𝑥2 + 𝑏𝑥 + 𝑐
𝑏2 − 4𝑎𝑐 < 0
𝑎𝑥2 + 𝑏𝑥 + 𝑐 k
𝑏2 − 4𝑎𝑐 < 0
2
+2 -1
= + +
(2 -1)( +2) (2 -1) ( +2)
x x A B C
dx dx
x x x x x x
3 2 2 2
4 4
= = + +
- - +1 ( +1)( -1) +1 -1 ( -1)
repeated partial fraction decomposition
linear
factor
x x A B C
dx dx dx
x x x x x x x x
2 2
-1 -1
=
4 -4 +3 (2 -1) +2
proper completing the square
x x
dx dx
x x x
2 3
2 2 2 2 2
1- +2 - + +
= + +
( +1) +1 ( +1)
proper partial fraction decomposition
irreducible
x x x A Bx C Dx E
dx dx
x x x x x
Revision- Partial Fraction
© 2019 Dr Khoo Shin Yee