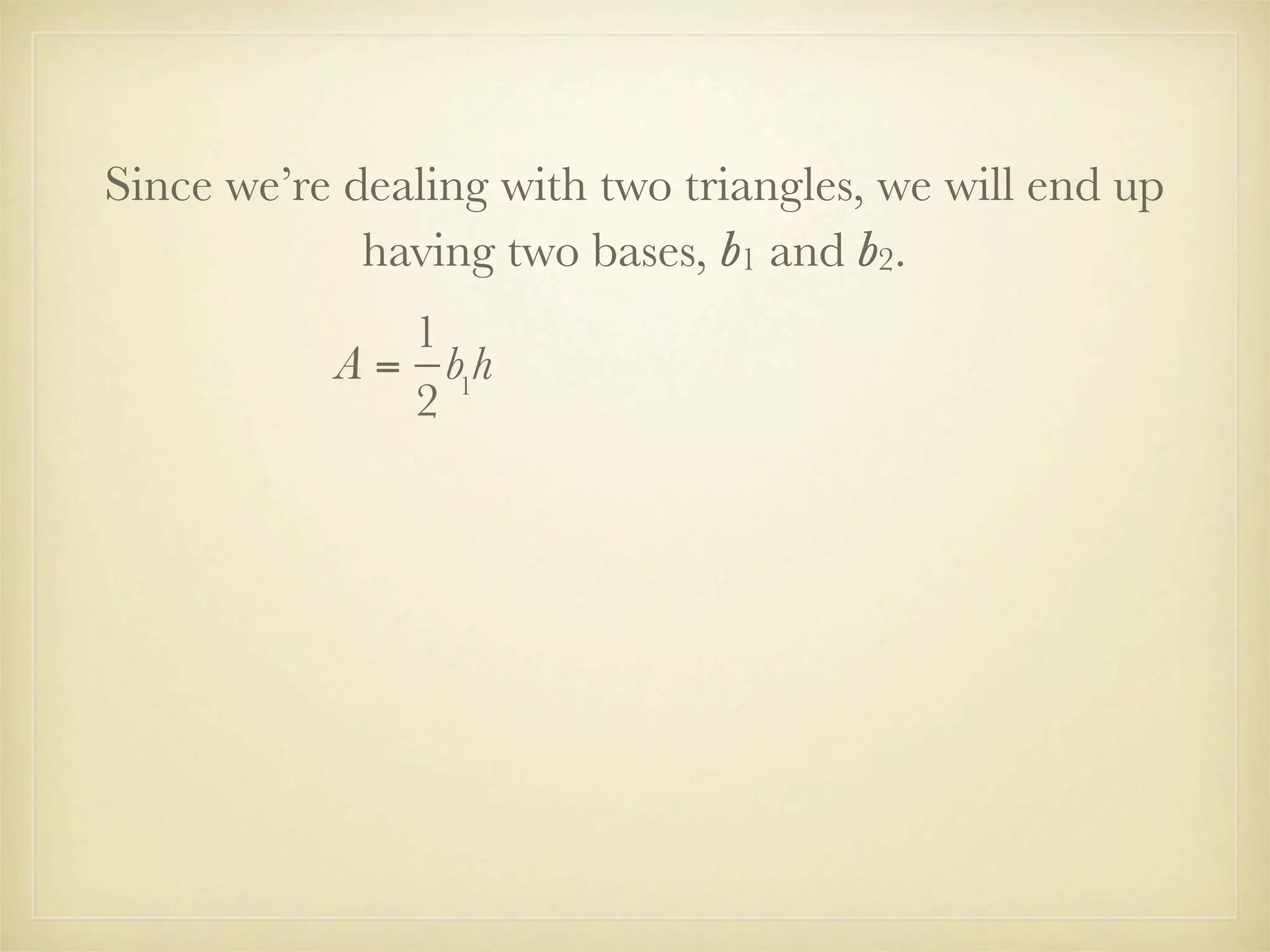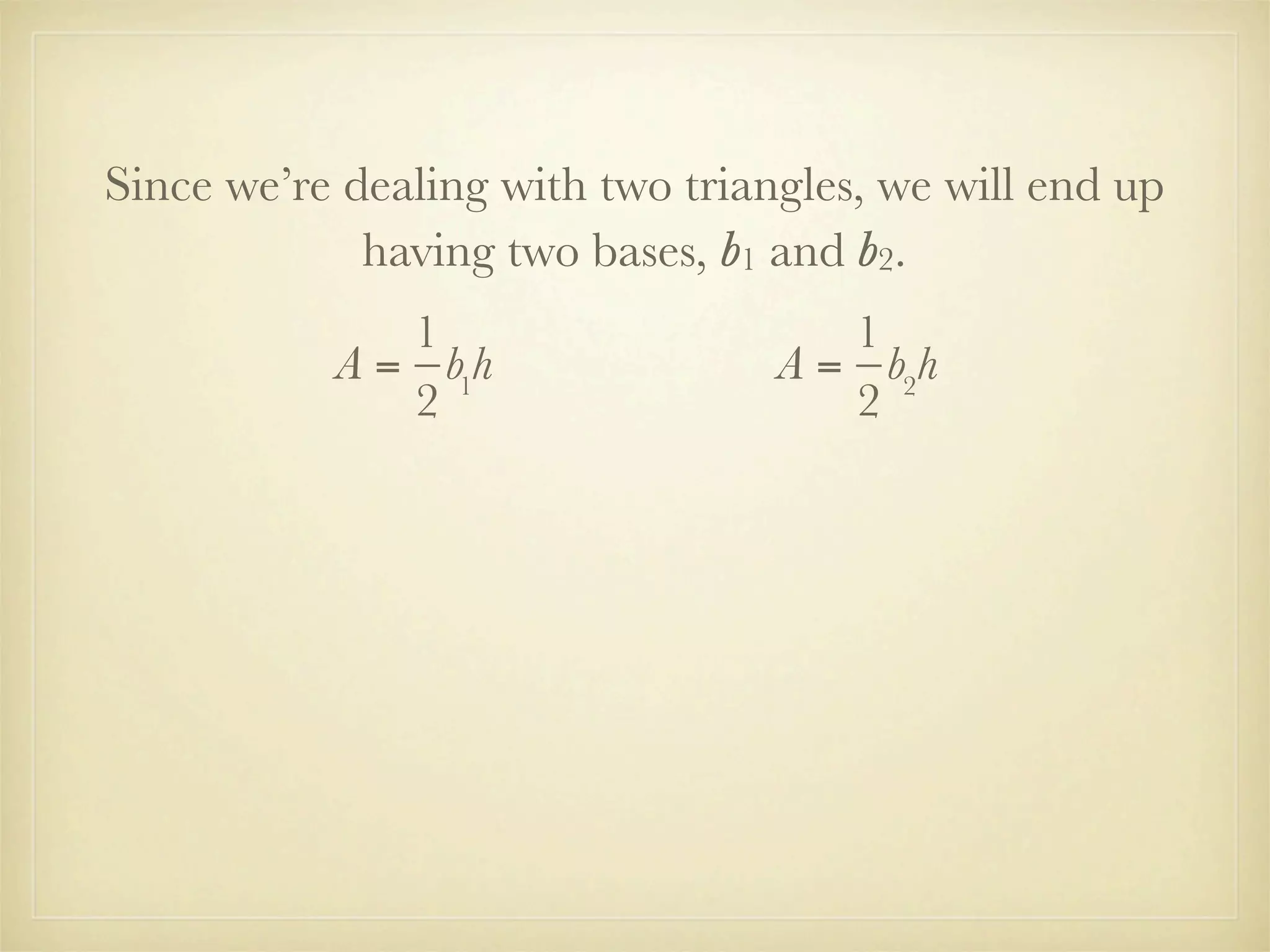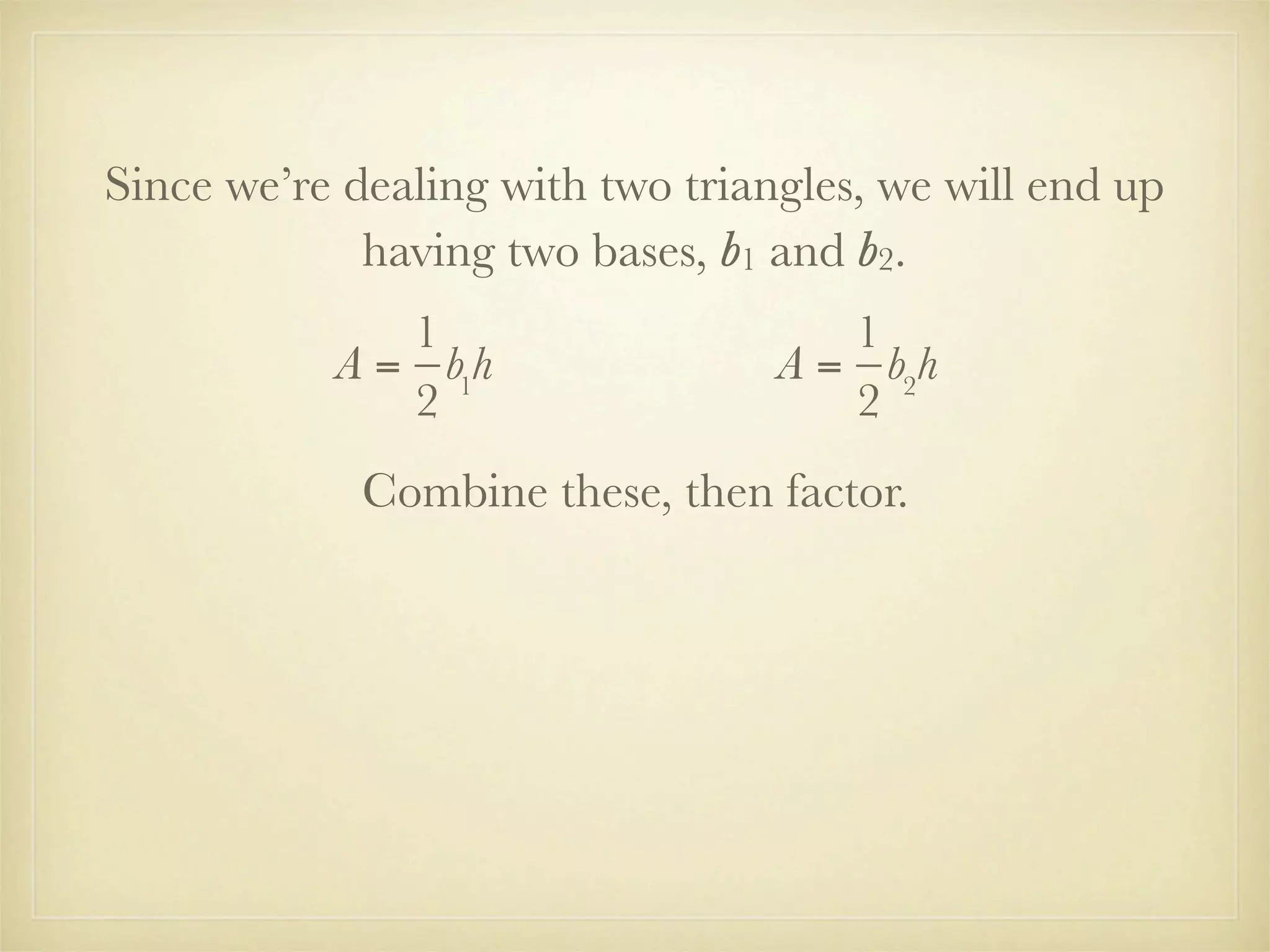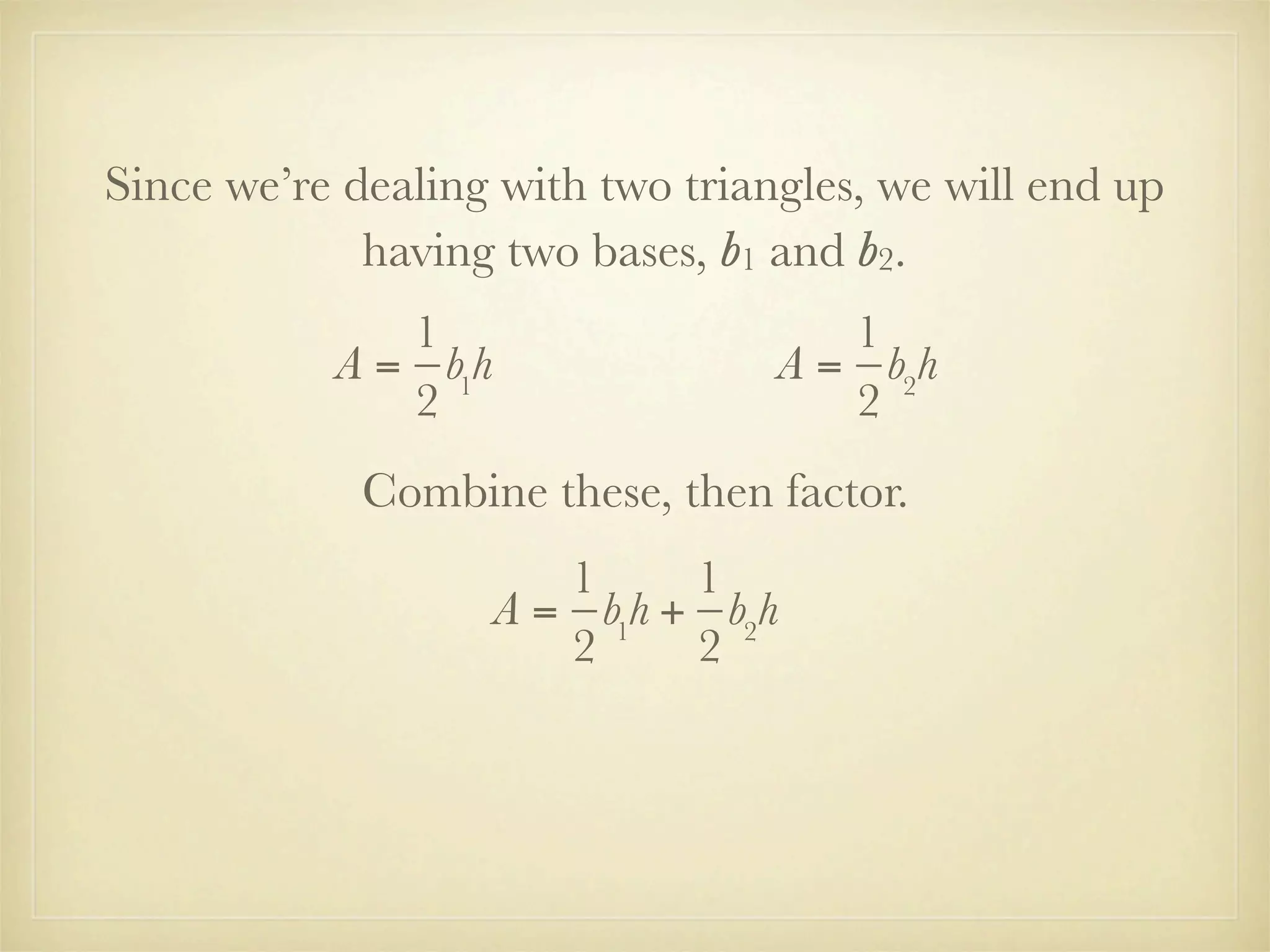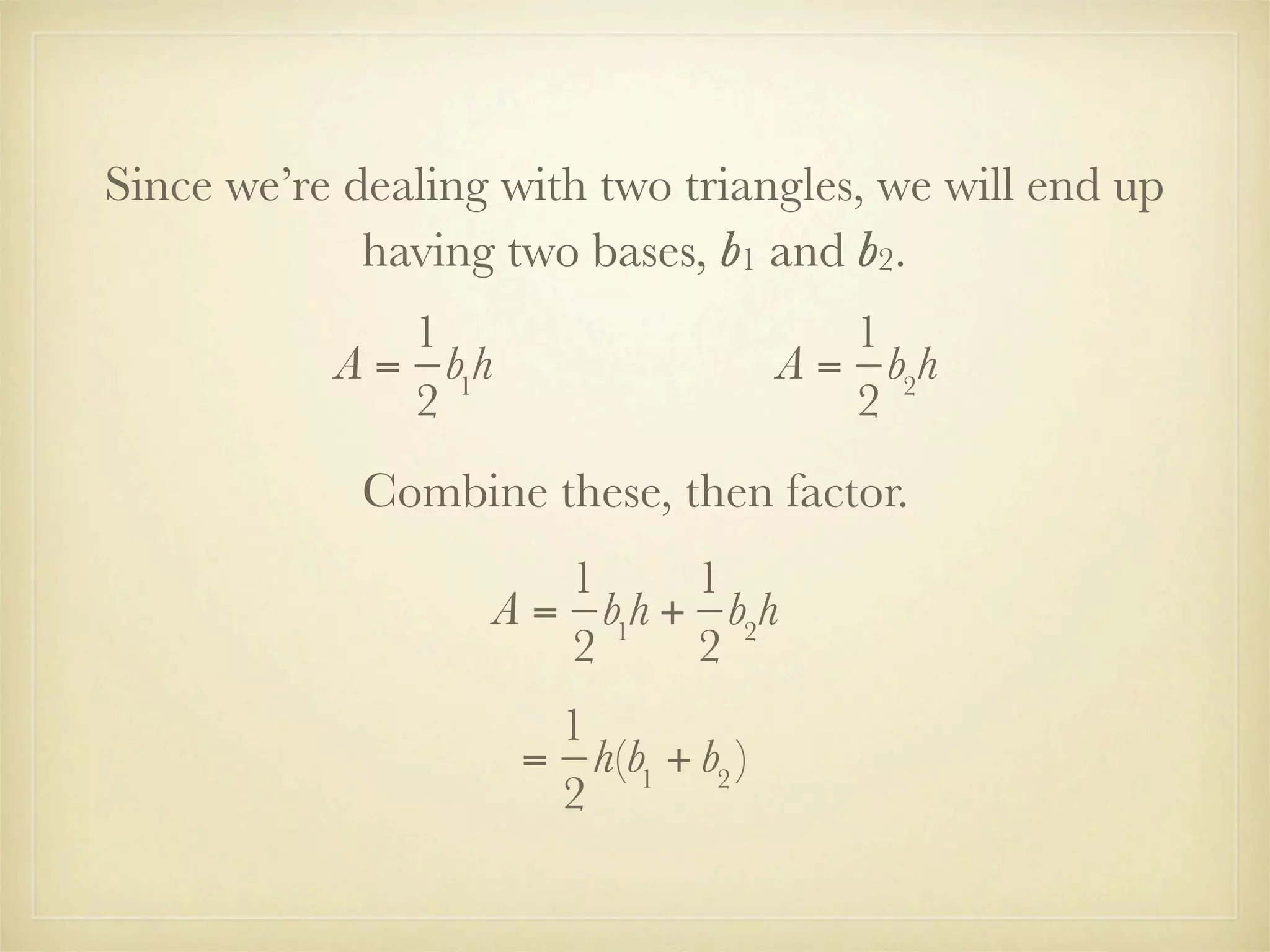This document provides instruction on factoring polynomials using the greatest common factor (GCF) method. It begins with an essential question and vocabulary definitions. It then walks through examples of factoring different polynomials step-by-step. The examples demonstrate finding the common factors of terms and variables and leaving the GCF outside parentheses. The document derives the formula for the area of a trapezoid and factors it out to show the process. It concludes with a problem set involving multiples of 3.

1. Section 9-7
Factoring using the Greatest Common
Factor (GCF)

2. Essential Question
• How do you factor polynomials using the Greatest
Common Factor?
• Where you’ll see this:
• Finance, geography, physics, modeling

3. Vocabulary
1. Factoring:

4. Vocabulary
1. Factoring: Breaking down a polynomial into two things
that multiply to get that polynomial.

5. Finding the GCF

6. Finding the GCF
1. Find a common factor for the numbers.

7. Finding the GCF
1. Find a common factor for the numbers.
2. Find common factors for each variable.

8. Finding the GCF
1. Find a common factor for the numbers.
2. Find common factors for each variable.
3. Leave the GCF out, then determine what’s left over
for inside the parentheses.

9. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
2 2 2 2
3 2 2
c. 4ab + 8a b d. 3x y − 6xy +12x y

10. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b(
2 2 2 2
3 2 2
c. 4ab + 8a b d. 3x y − 6xy +12x y

11. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b( a − c)
2 2 2 2
3
c. 4ab + 8a b 2 2
d. 3x y − 6xy +12x y

12. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b( a − c) 2h(
2 2 2 2
3
c. 4ab + 8a b 2 2
d. 3x y − 6xy +12x y

13. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b( a − c) 2h( 8h + 5)
2 2 2 2
3
c. 4ab + 8a b 2 2
d. 3x y − 6xy +12x y

14. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b( a − c) 2h( 8h + 5)
2 2 2 2
3
c. 4ab + 8a b 2 2
d. 3x y − 6xy +12x y
2
4ab (

15. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b( a − c) 2h( 8h + 5)
2 2 2 2
3
c. 4ab + 8a b 2 2
d. 3x y − 6xy +12x y
2
4ab ( b + 2a)

16. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b( a − c) 2h( 8h + 5)
2 2 2 2
3
c. 4ab + 8a b 2 2
d. 3x y − 6xy +12x y
2
4ab ( b + 2a)
2
4ab (2a + b)

17. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b( a − c) 2h( 8h + 5)
2 2 2 2
3
c. 4ab + 8a b 2 2
d. 3x y − 6xy +12x y
2
4ab ( b + 2a) 3xy(
2
4ab (2a + b)

18. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b( a − c) 2h( 8h + 5)
2 2 2 2
3
c. 4ab + 8a b 2 2
d. 3x y − 6xy +12x y
2
4ab ( b + 2a) 3xy( x − 2 y + 4xy)
2
4ab (2a + b)

19. Example 1
Factor.
a. 5ab − 5bc 2
b. 16h +10h
5b( a − c) 2h( 8h + 5)
2 2 2 2
3
c. 4ab + 8a b 2 2
d. 3x y − 6xy +12x y
2
4ab ( b + 2a) 3xy( x − 2 y + 4xy)
2
4ab (2a + b) 3xy(x + 4xy − 2 y)

20. Example 2
Since a trapezoid may be divided into two triangles, the
formula for the area of a trapezoid is obtained by adding
the areas of two triangles. Find this formula. Then factor
out the GCF.

21. Example 2
Since a trapezoid may be divided into two triangles, the
formula for the area of a trapezoid is obtained by adding
the areas of two triangles. Find this formula. Then factor
out the GCF.
First we need the area of a triangle:

22. Example 2
Since a trapezoid may be divided into two triangles, the
formula for the area of a trapezoid is obtained by adding
the areas of two triangles. Find this formula. Then factor
out the GCF.
First we need the area of a triangle:
1
A = bh
2

23. Since we’re dealing with two triangles, we will end up
having two bases, b1 and b2.

24. Since we’re dealing with two triangles, we will end up
having two bases, b1 and b2.
1
A = b1h
2

25. Since we’re dealing with two triangles, we will end up
having two bases, b1 and b2.
1 1
A = b1h A = b2h
2 2

26. Since we’re dealing with two triangles, we will end up
having two bases, b1 and b2.
1 1
A = b1h A = b2h
2 2
Combine these, then factor.

27. Since we’re dealing with two triangles, we will end up
having two bases, b1 and b2.
1 1
A = b1h A = b2h
2 2
Combine these, then factor.
1 1
A = b1h + b2h
2 2

28. Since we’re dealing with two triangles, we will end up
having two bases, b1 and b2.
1 1
A = b1h A = b2h
2 2
Combine these, then factor.
1 1
A = b1h + b2h
2 2
1
= h(b1 + b2 )
2

29. Problem Set

30. Problem Set
p. 406 # 1-39, multiples of 3
“Actions have consequences...first rule of life. And the
second rule of life is this - you are the only one responsible
for your own actions.” - Holly Lisle