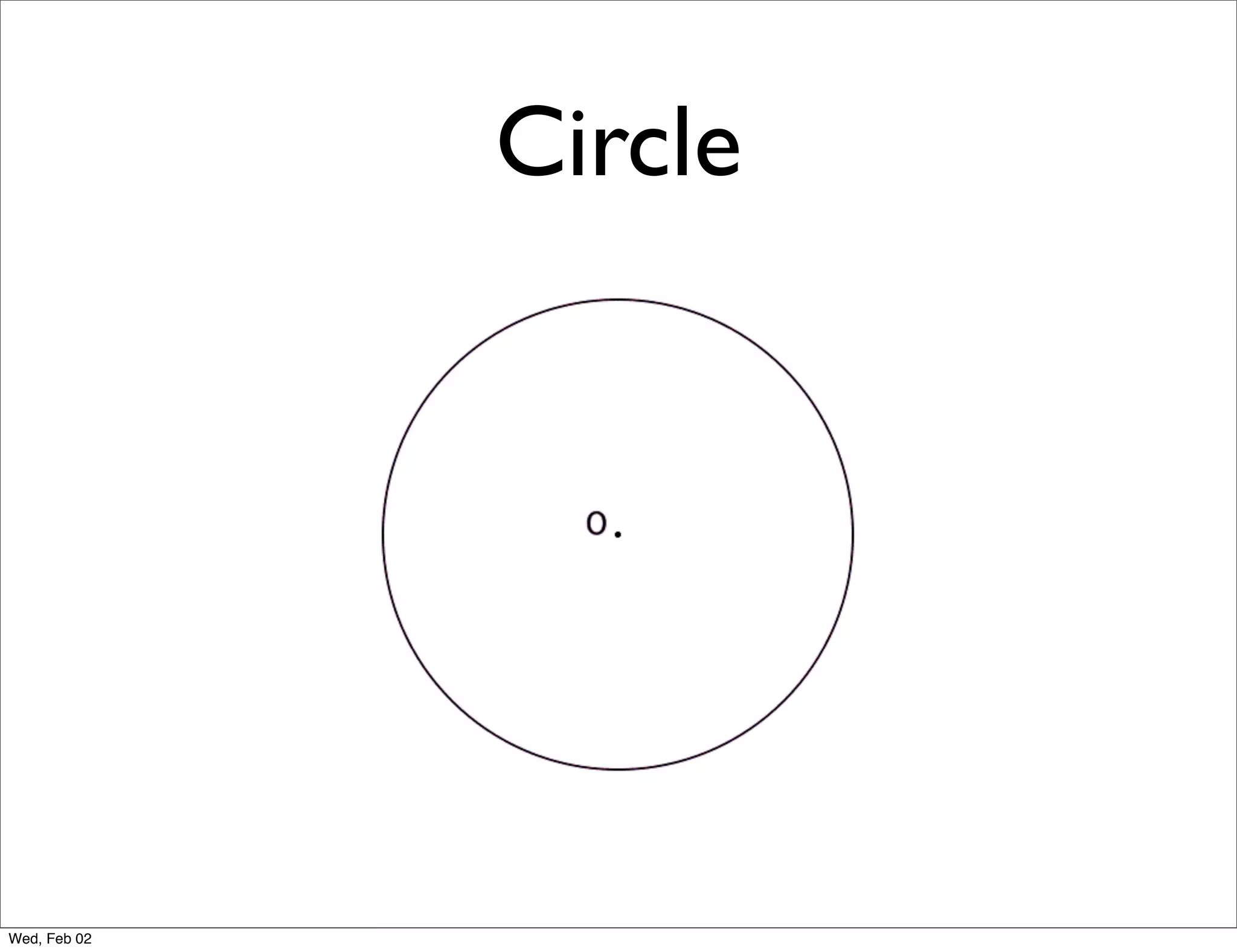
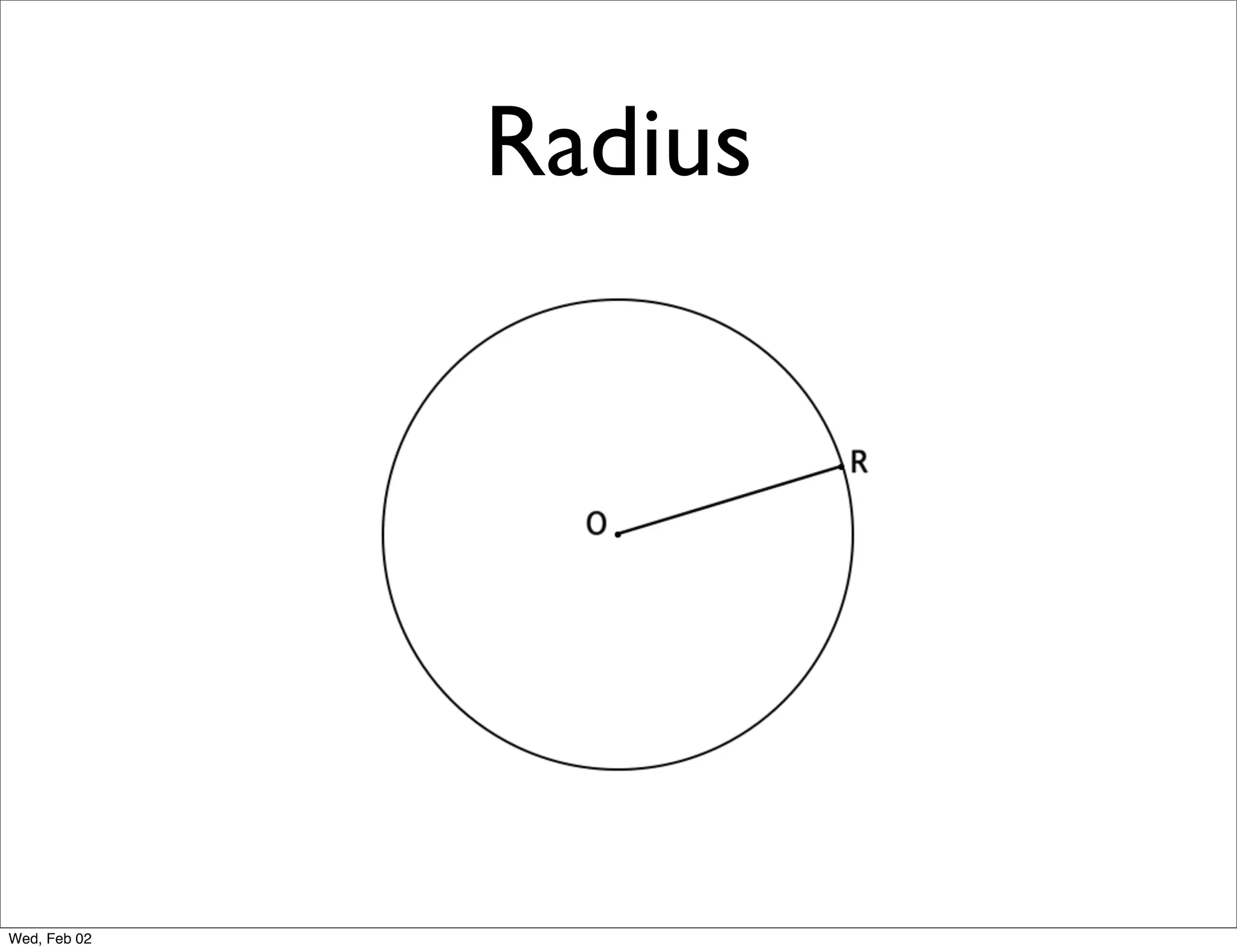
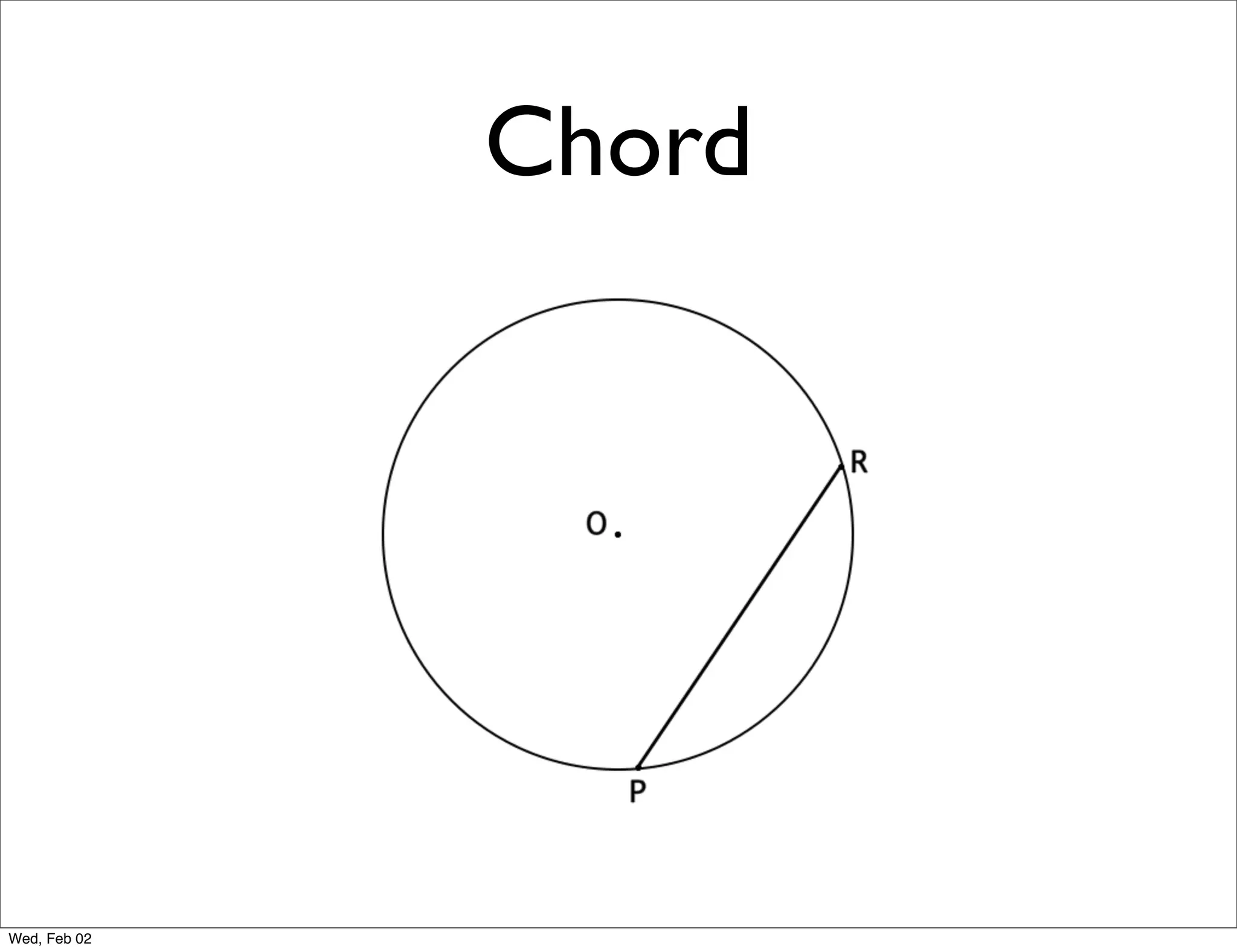
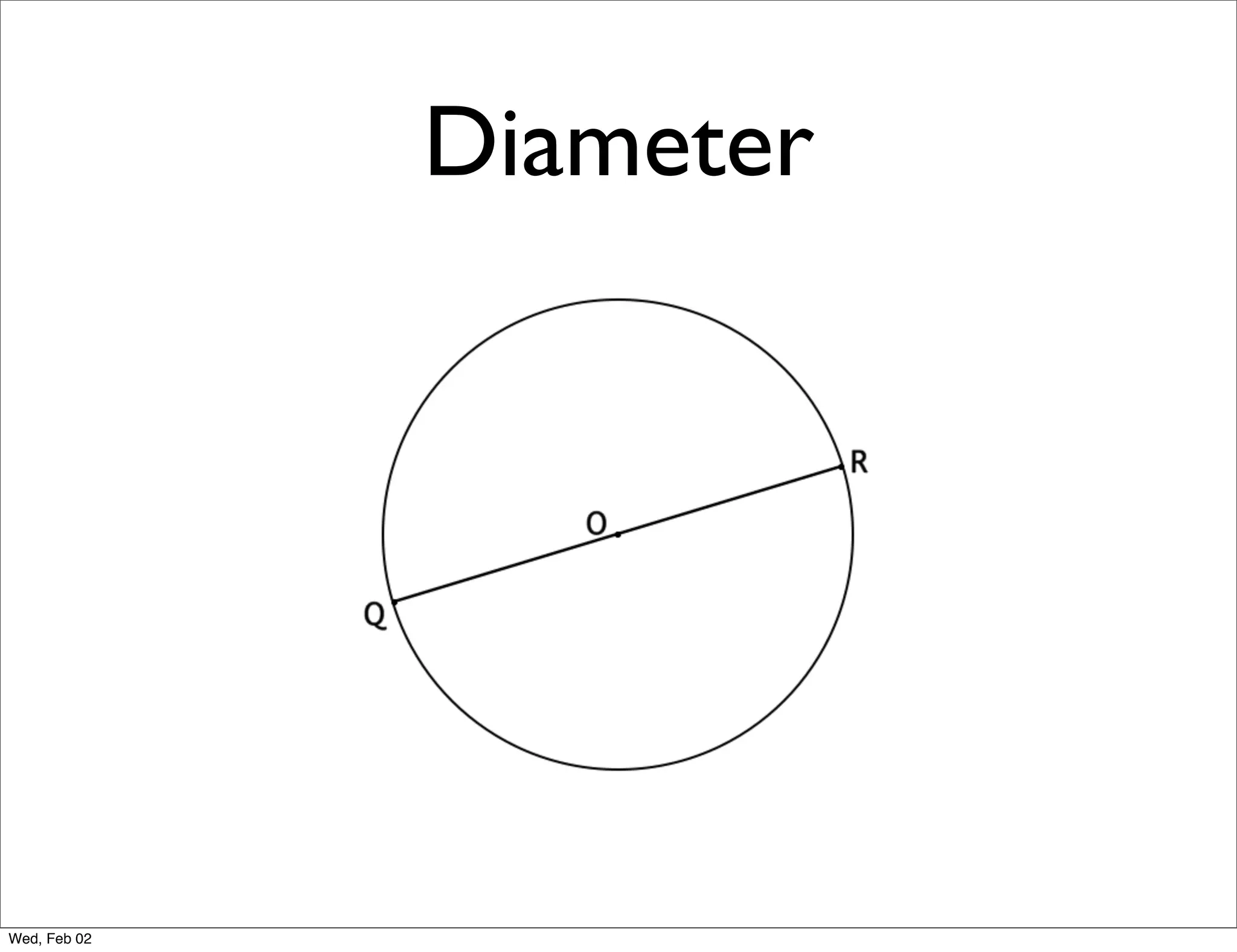
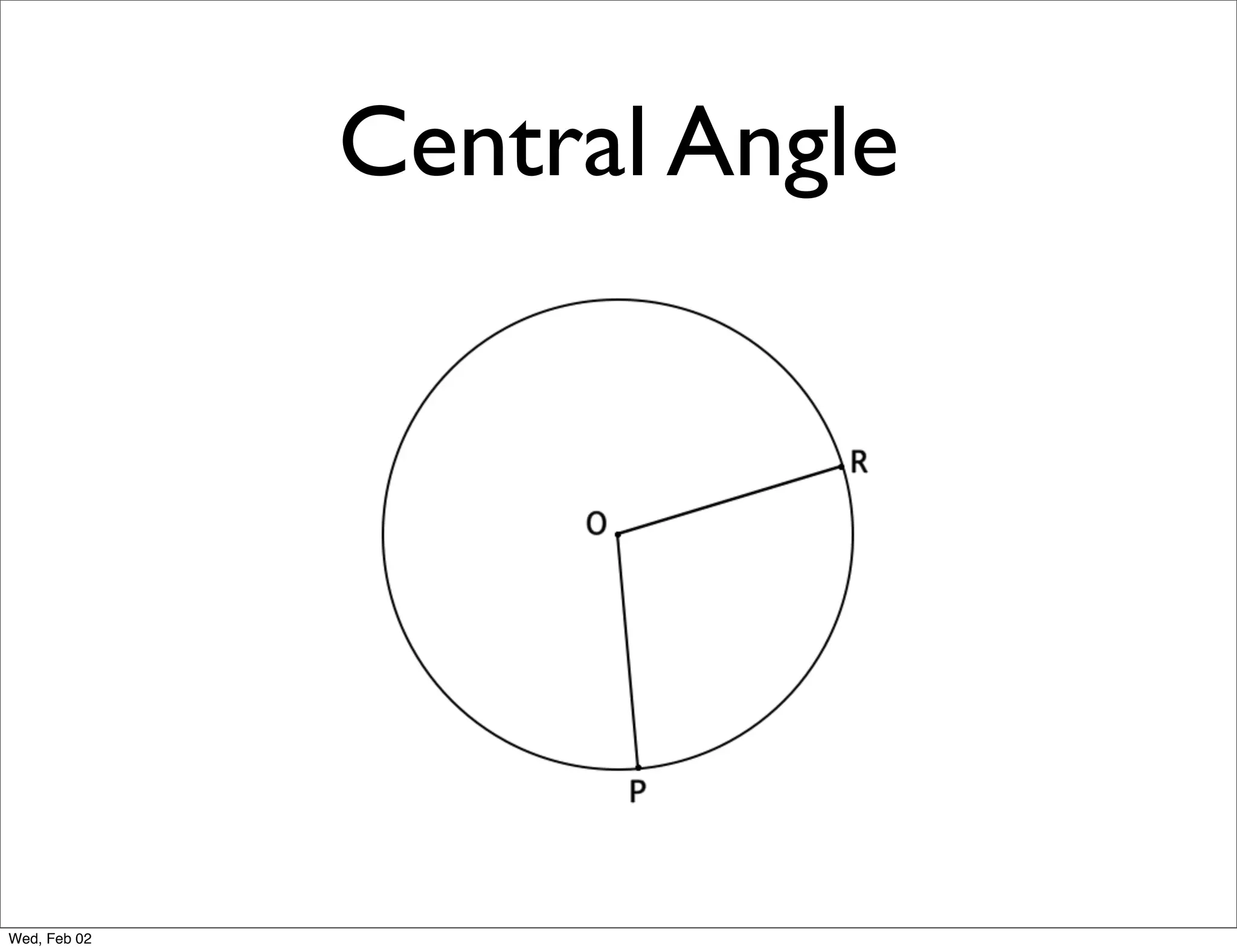
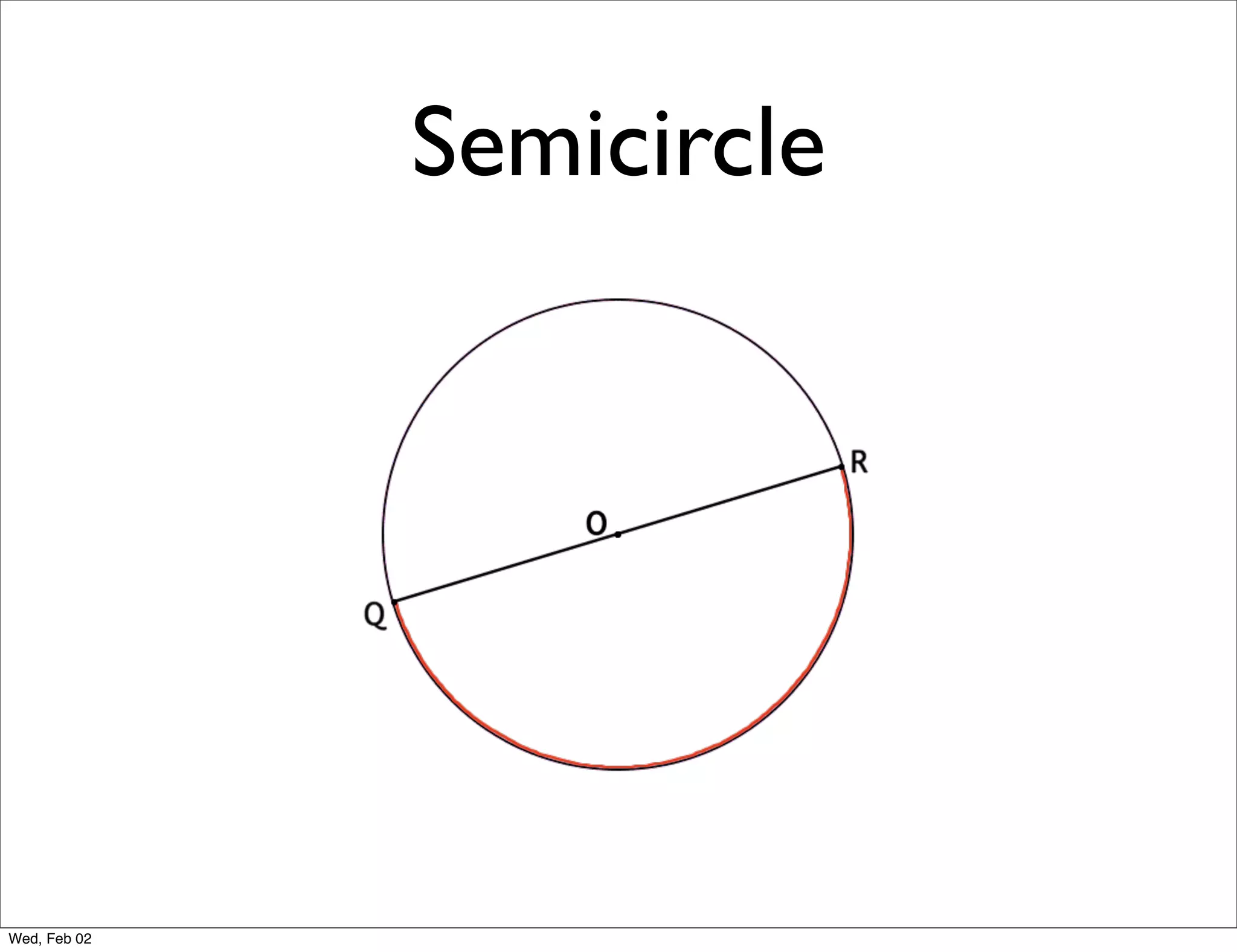
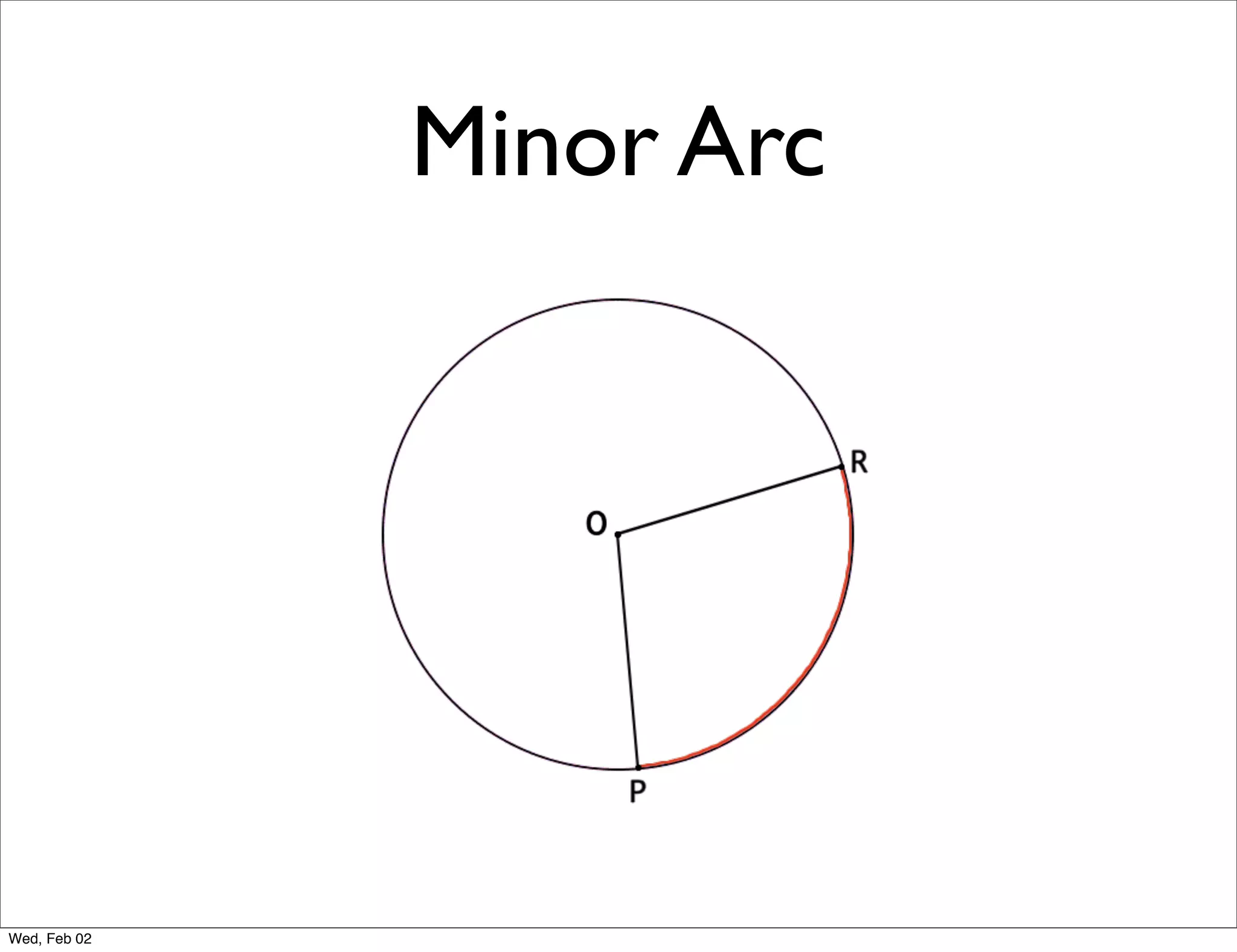
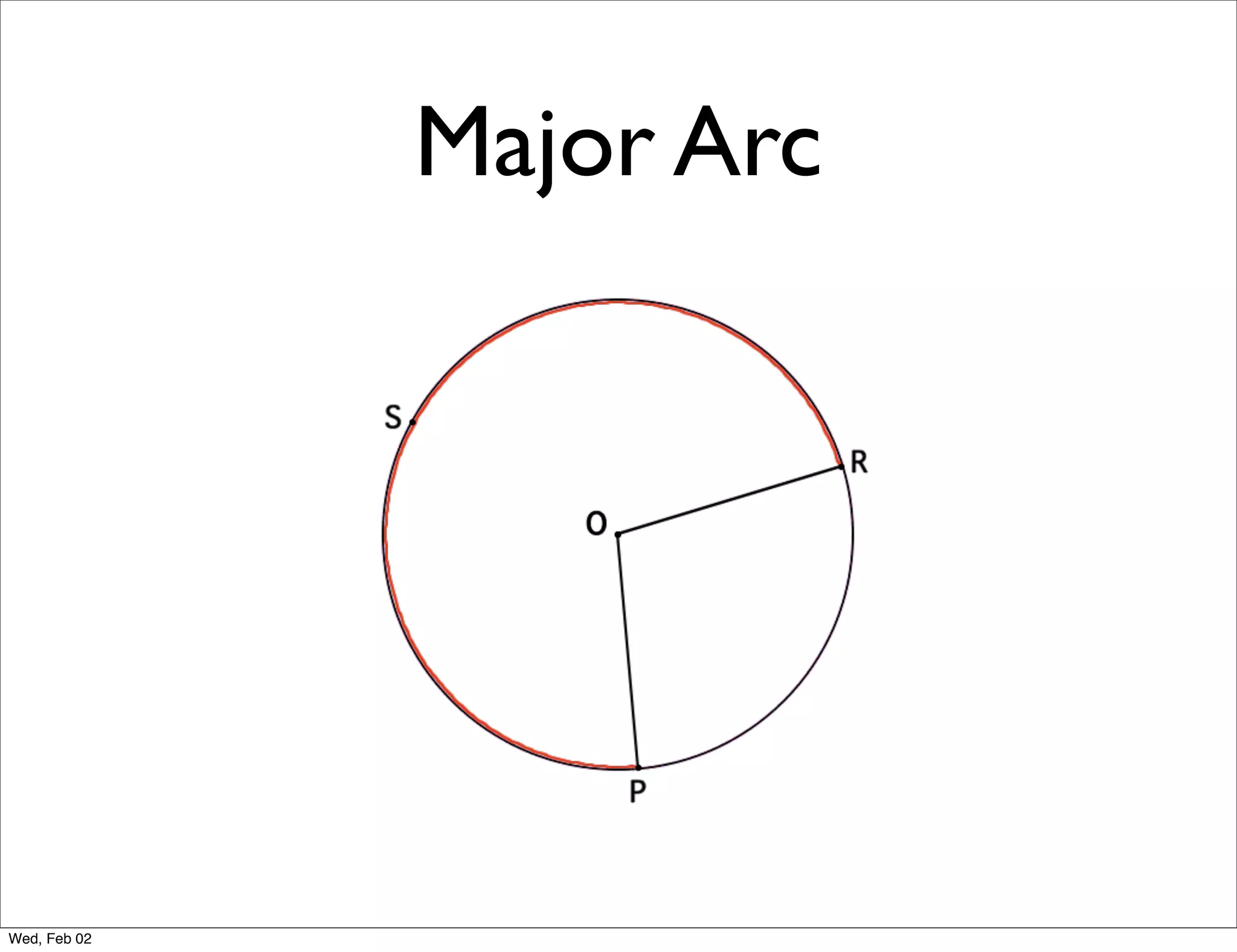
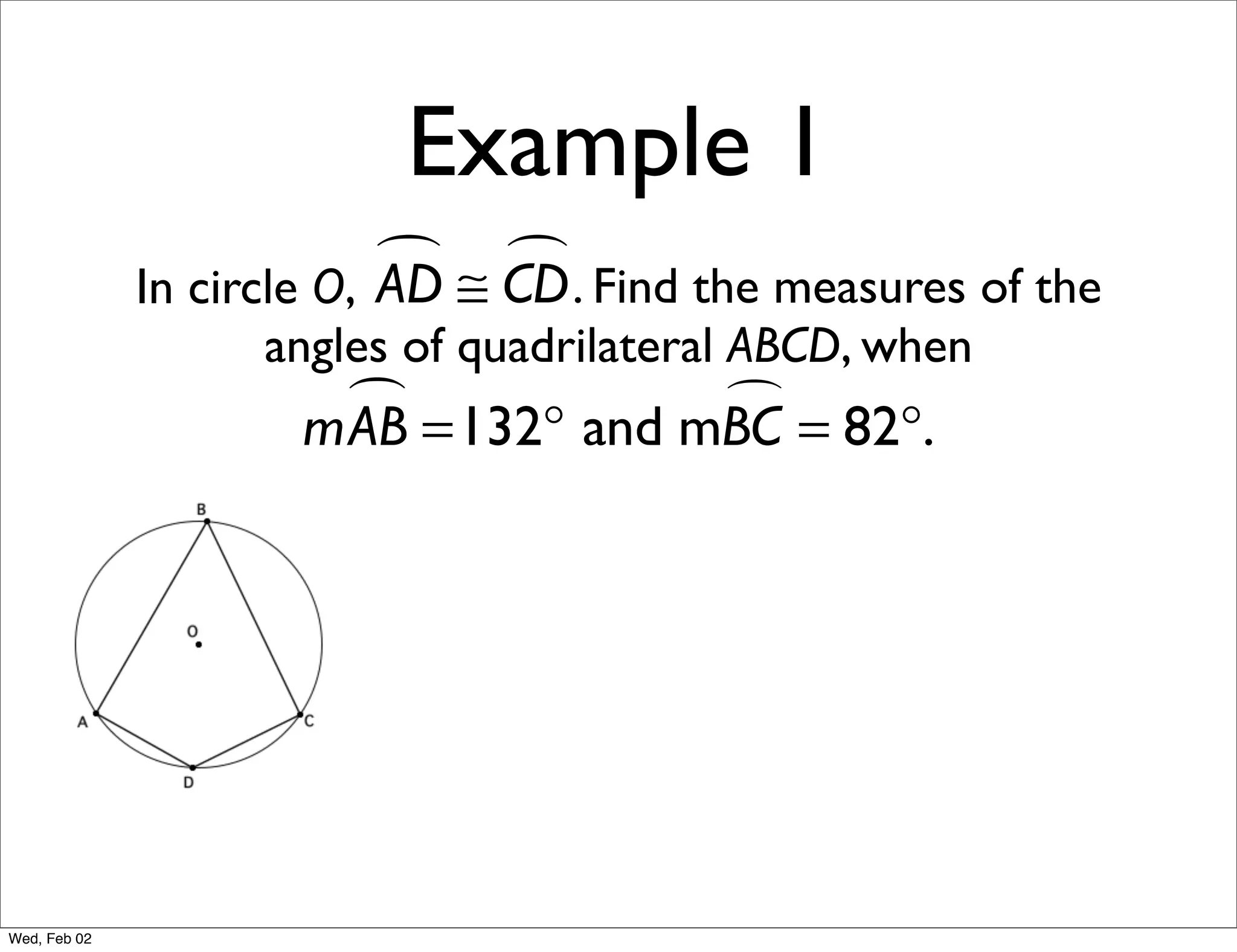
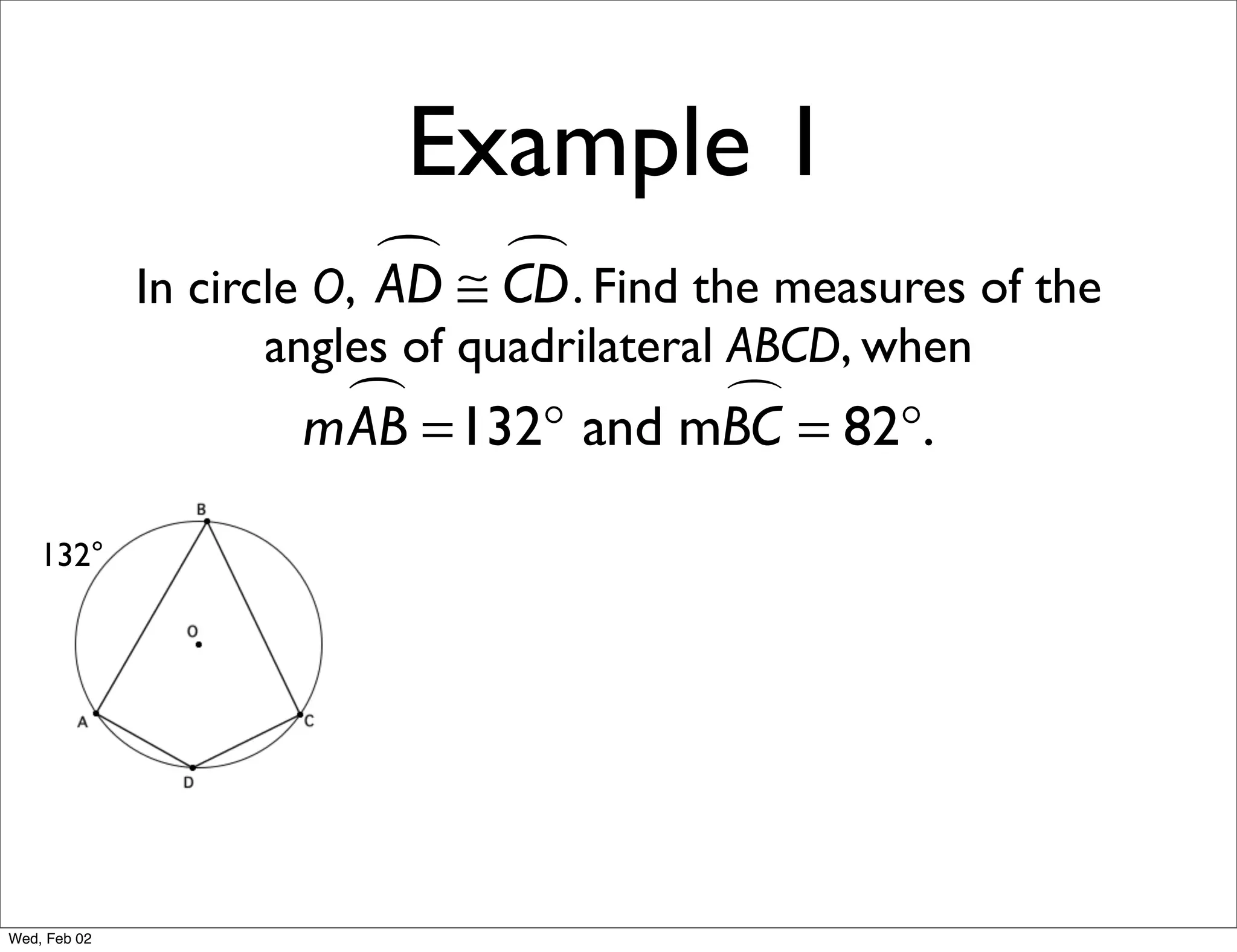
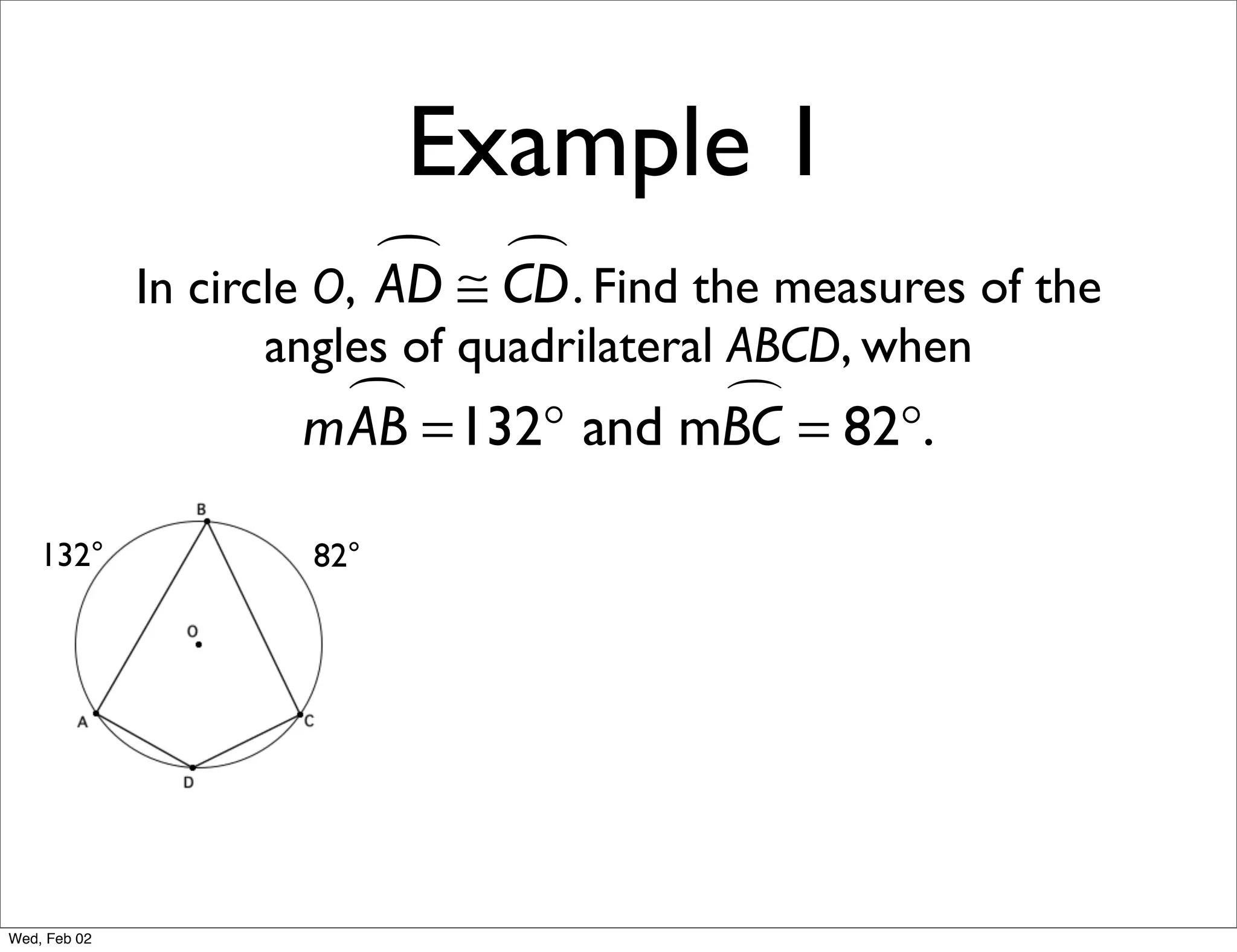
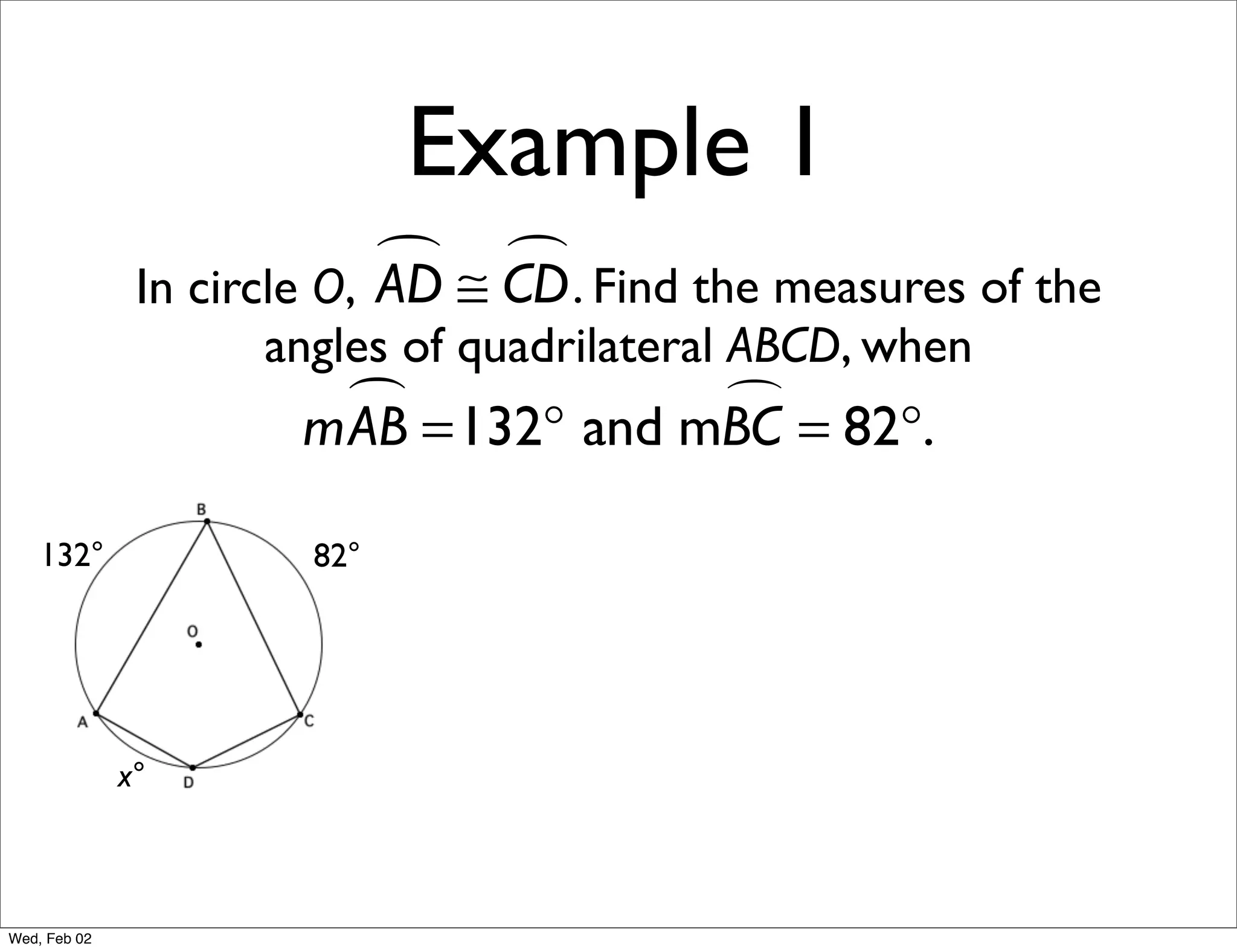
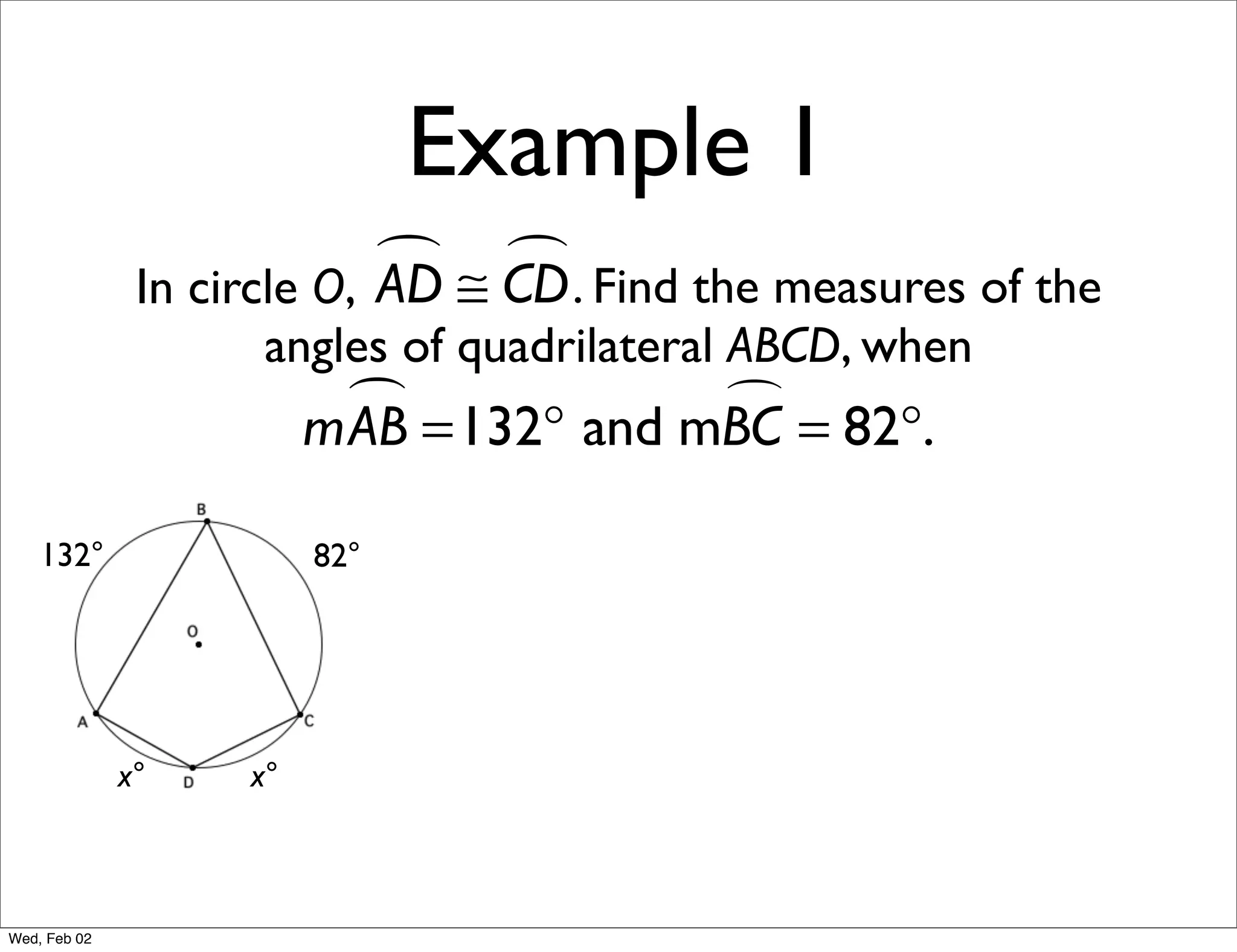
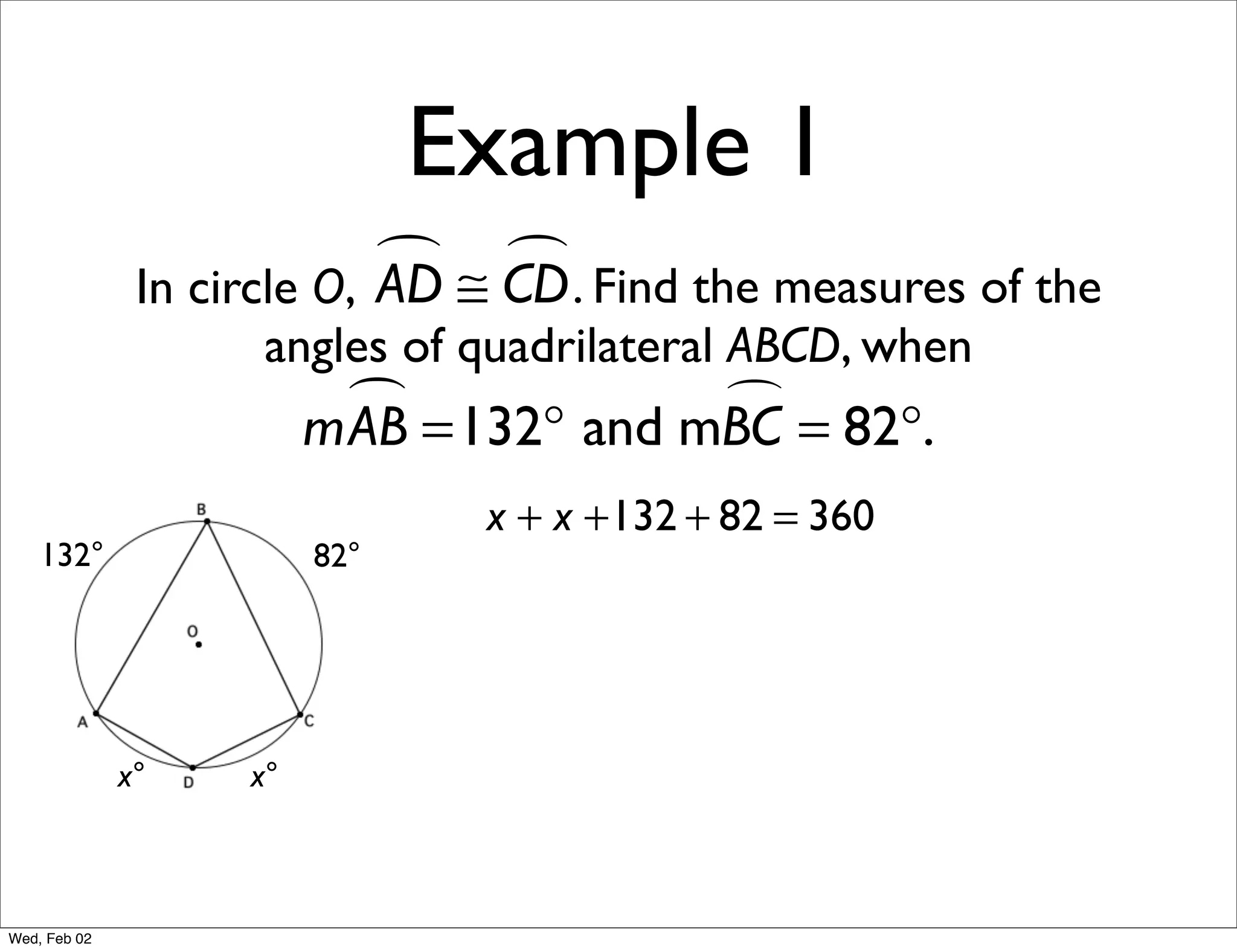
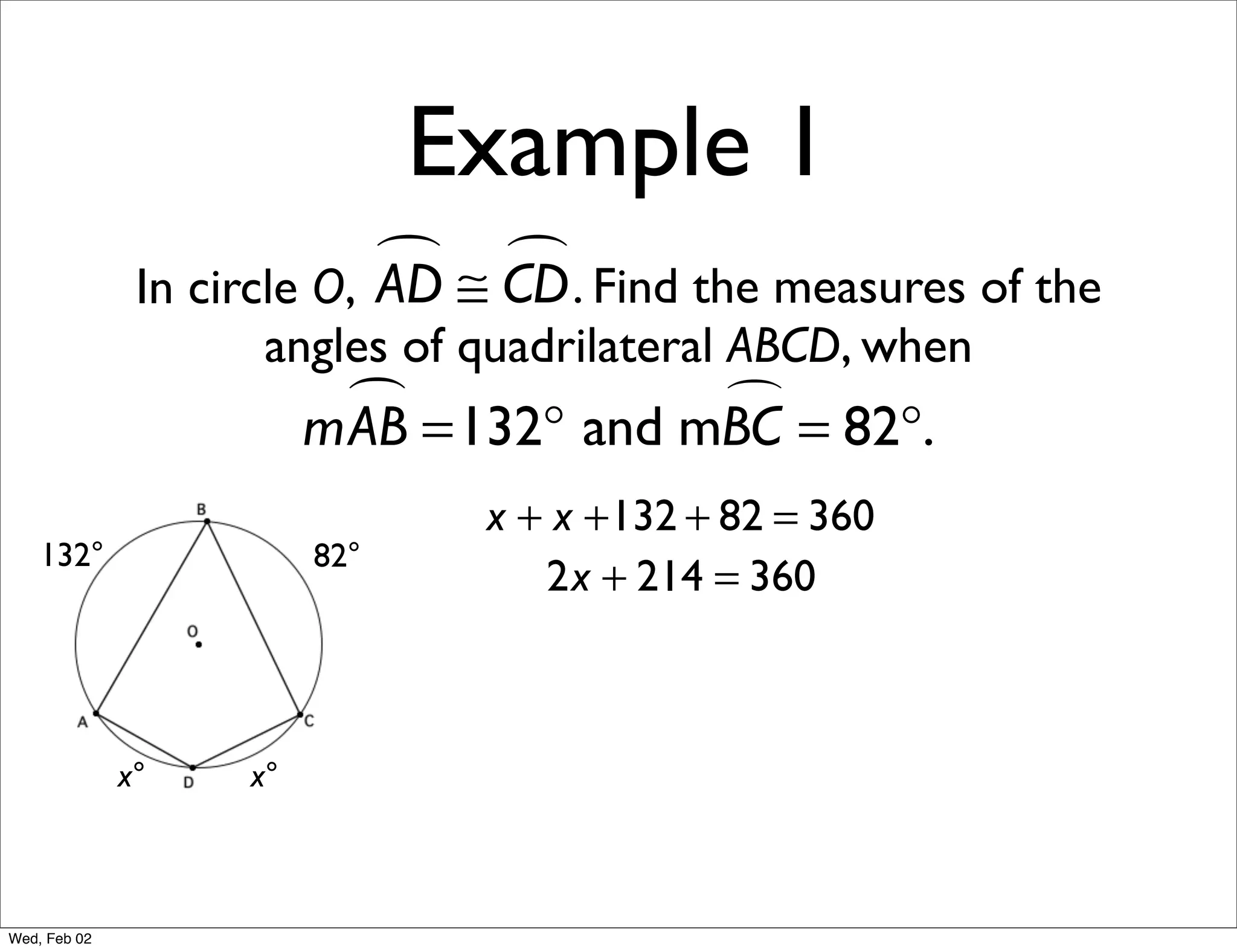
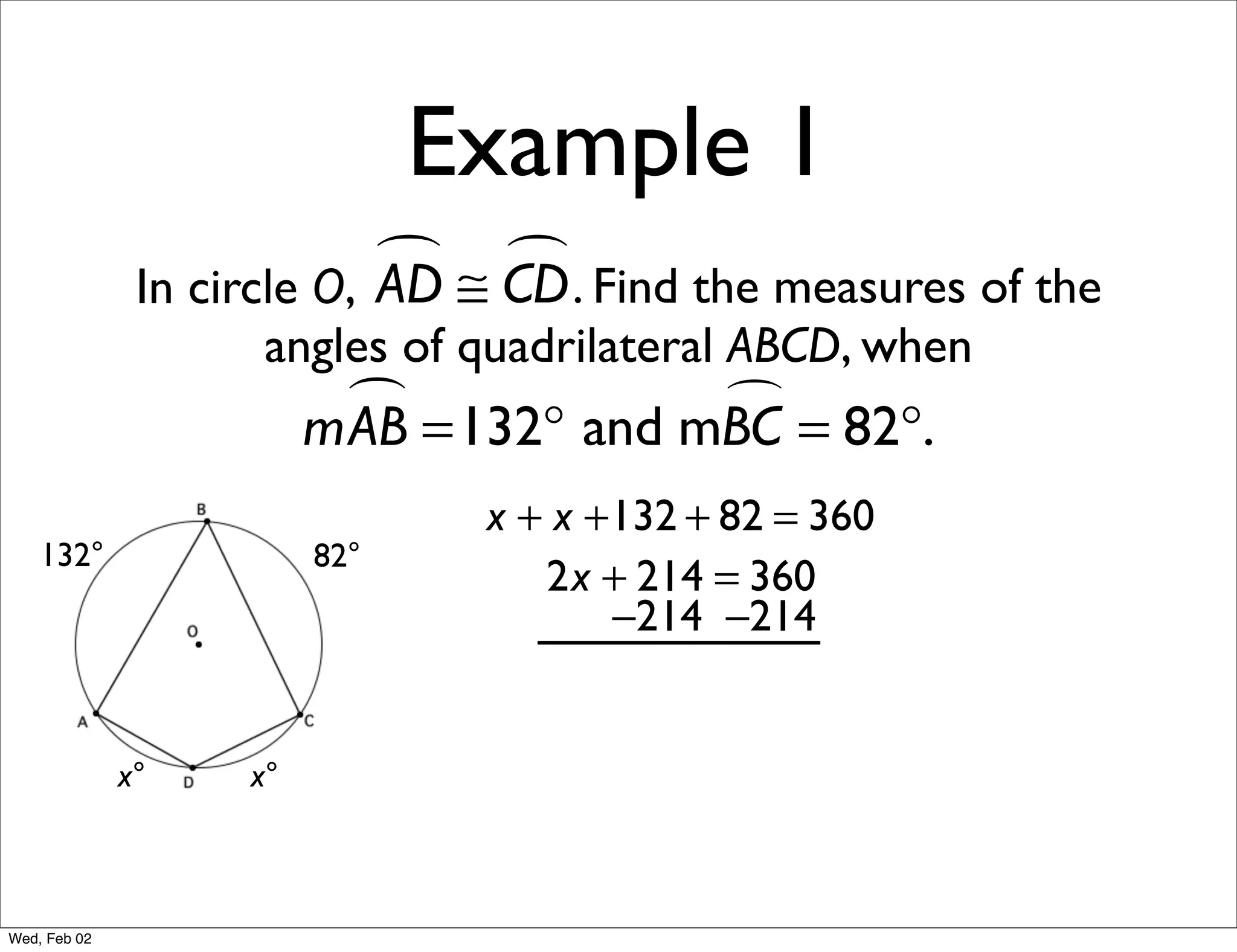
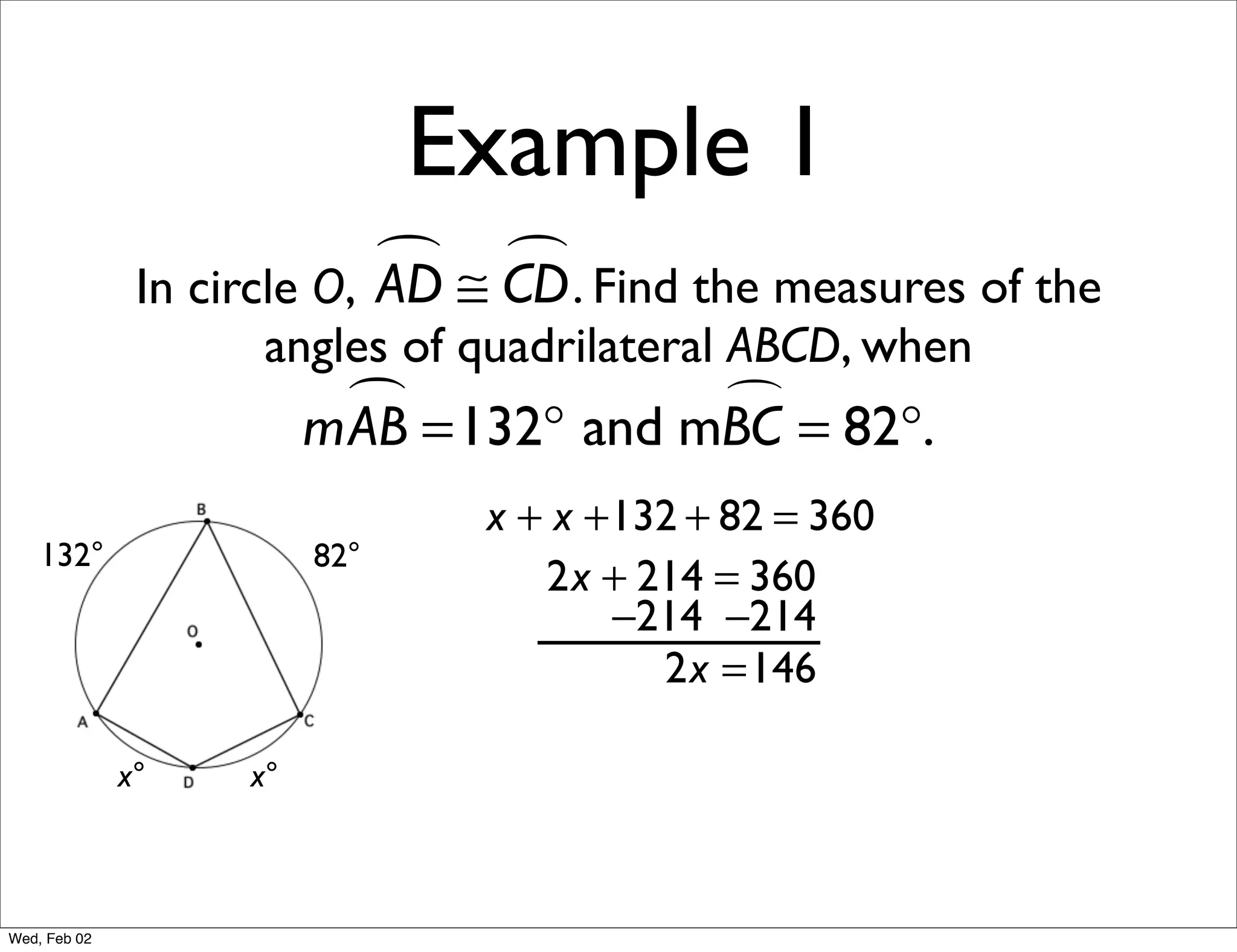
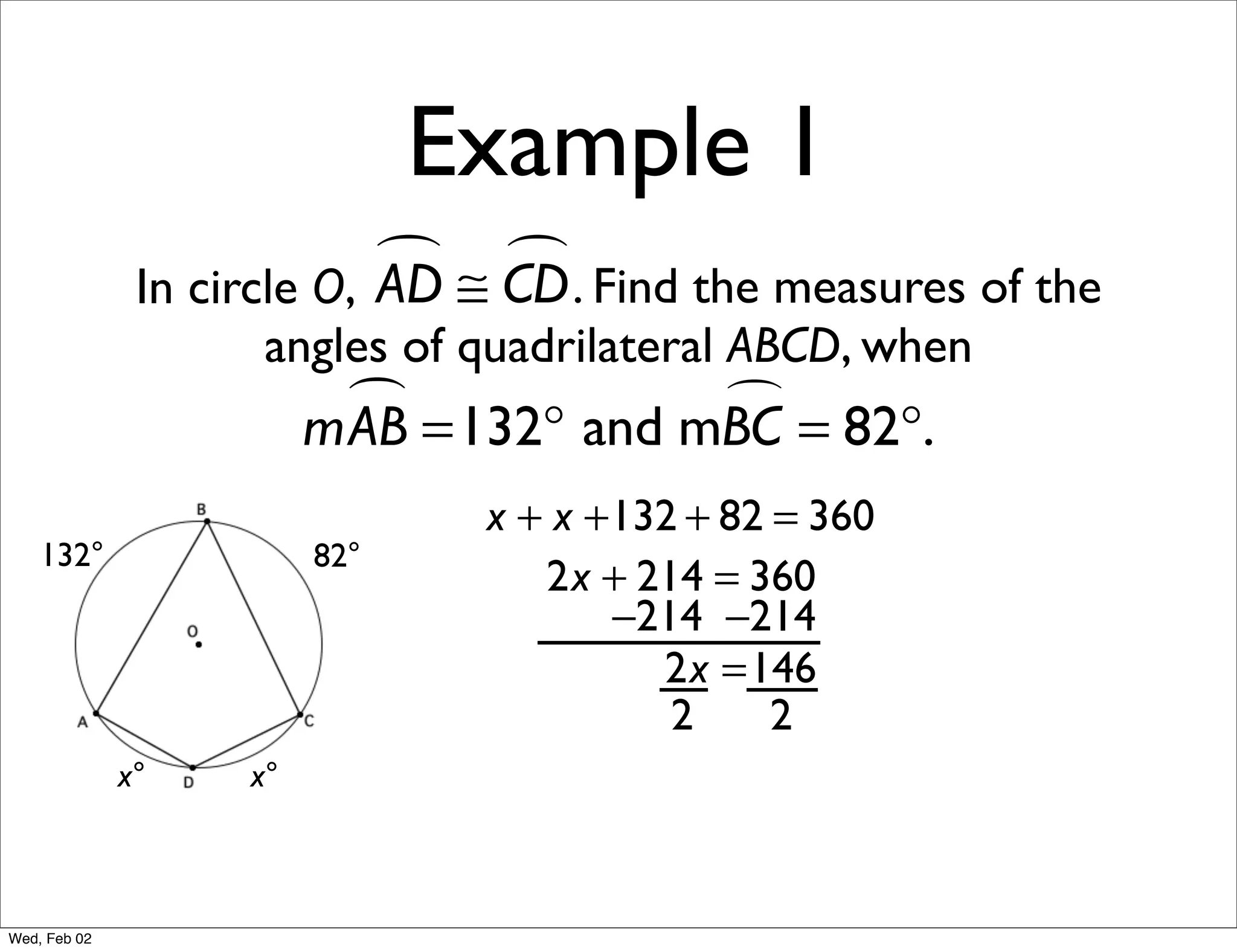
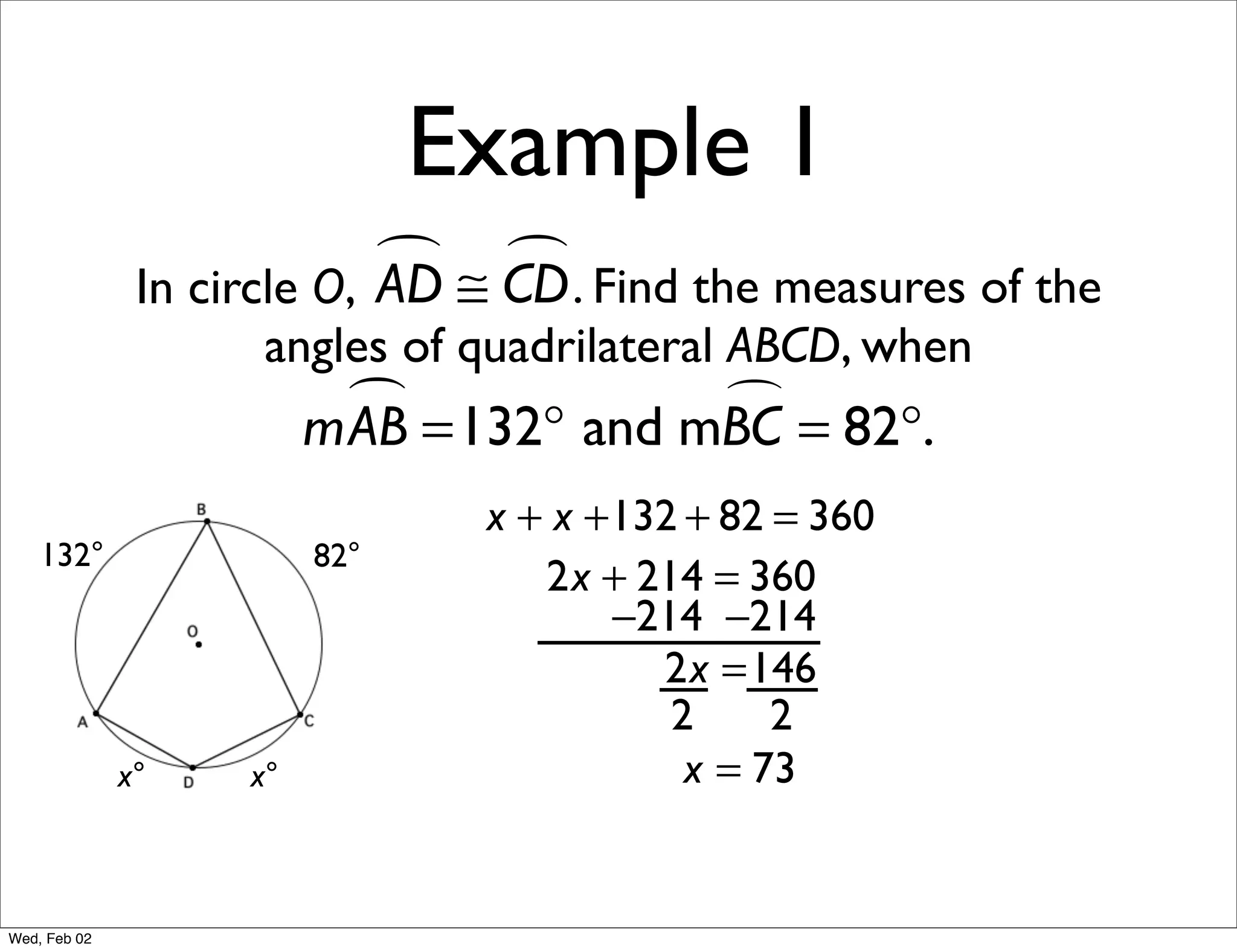
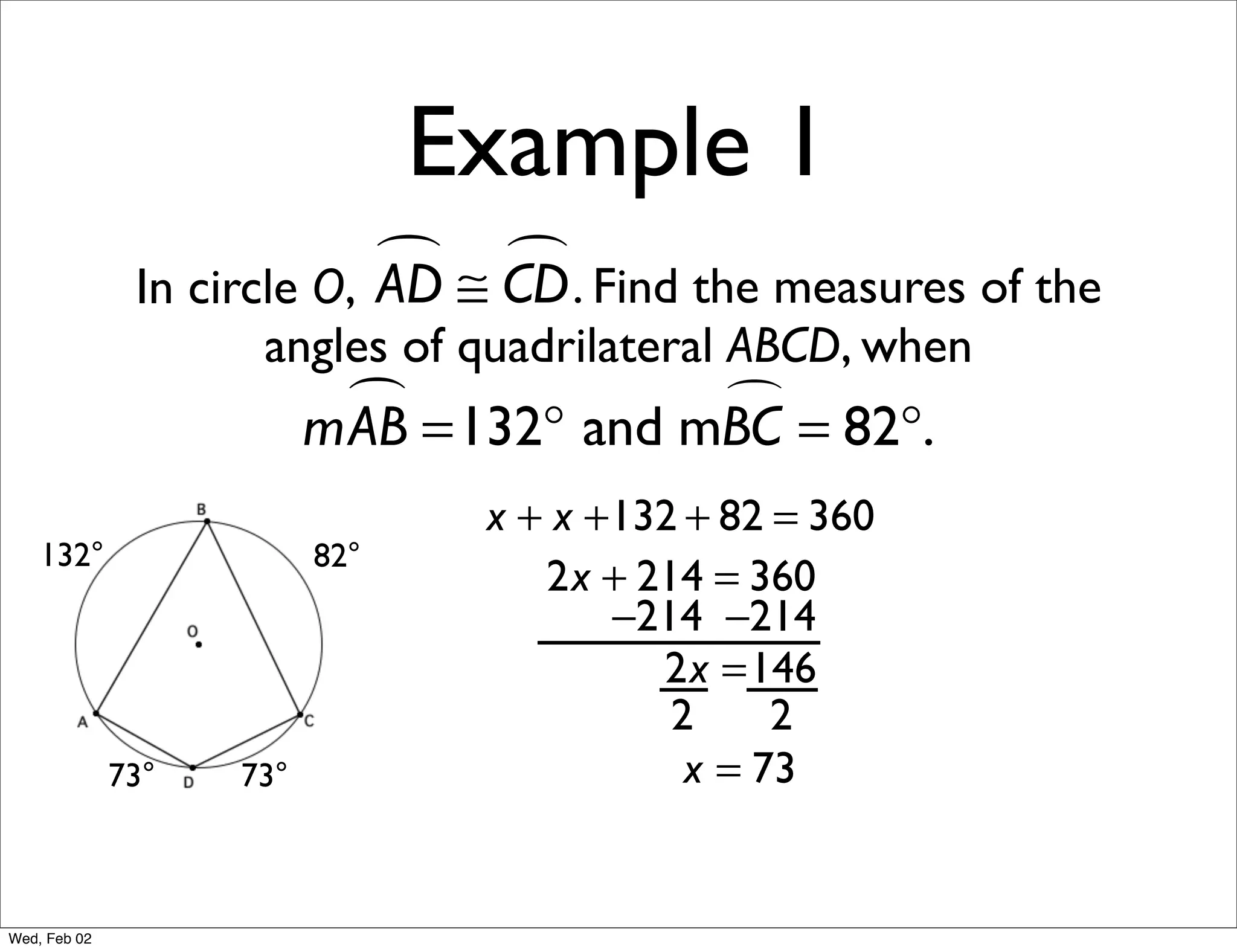
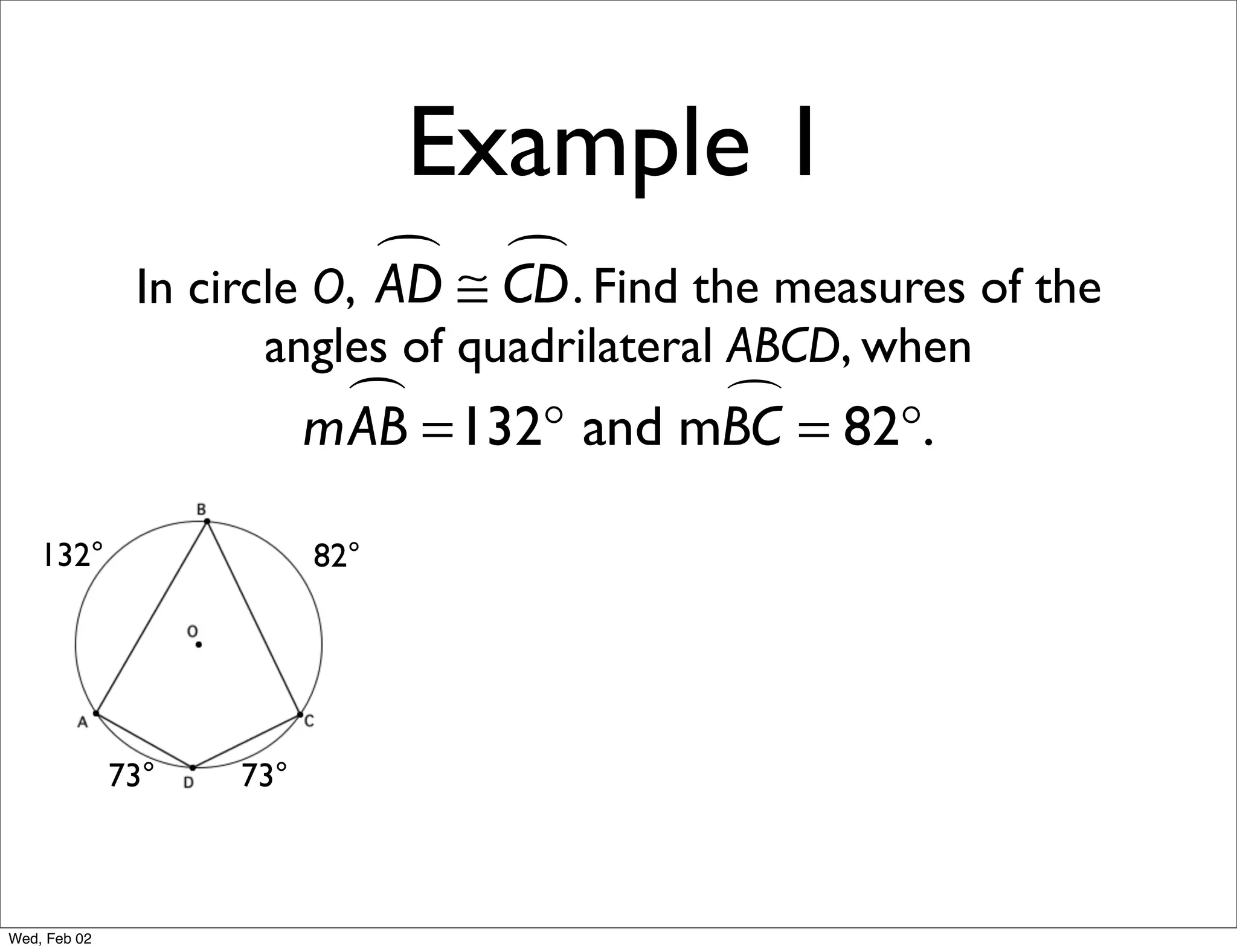
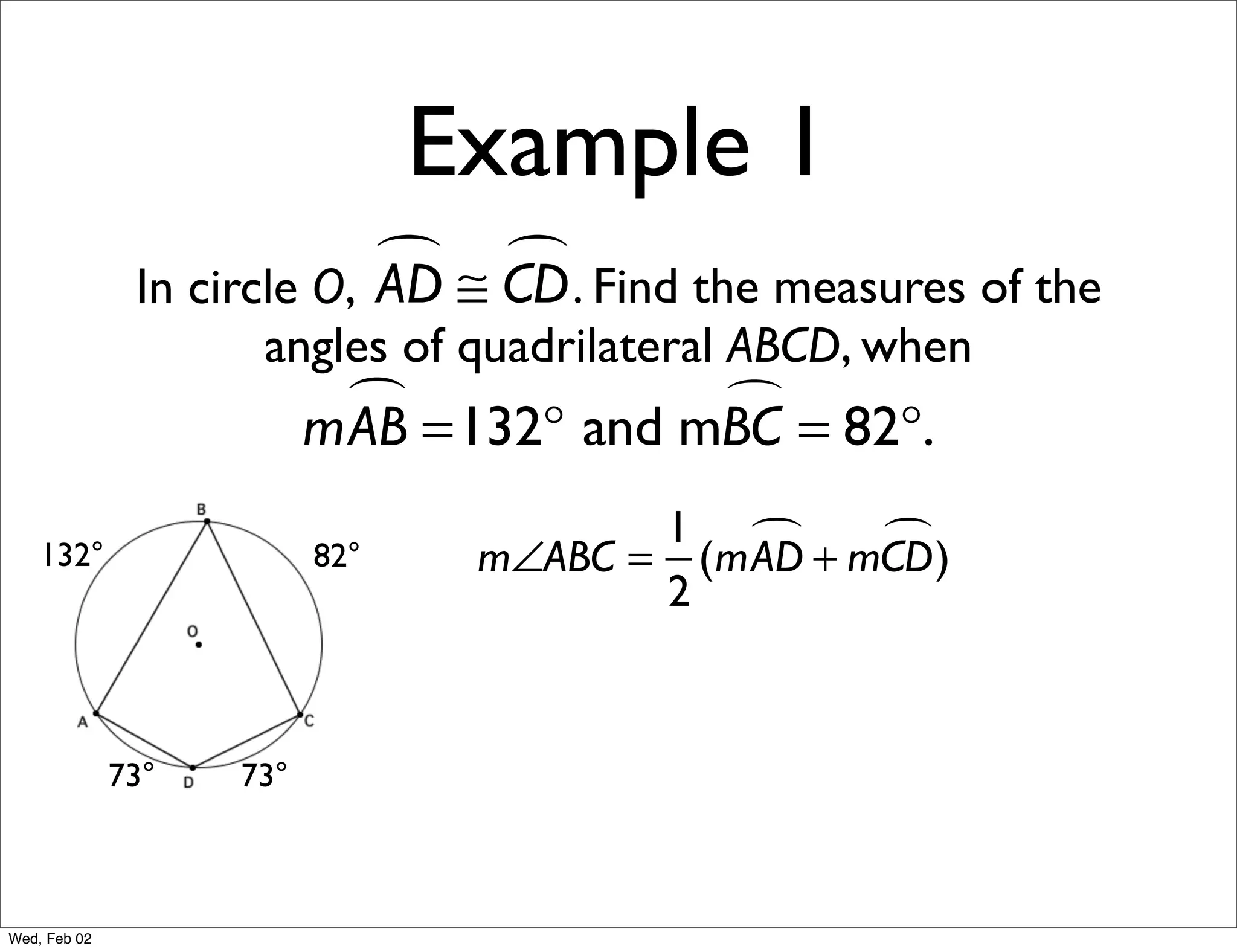
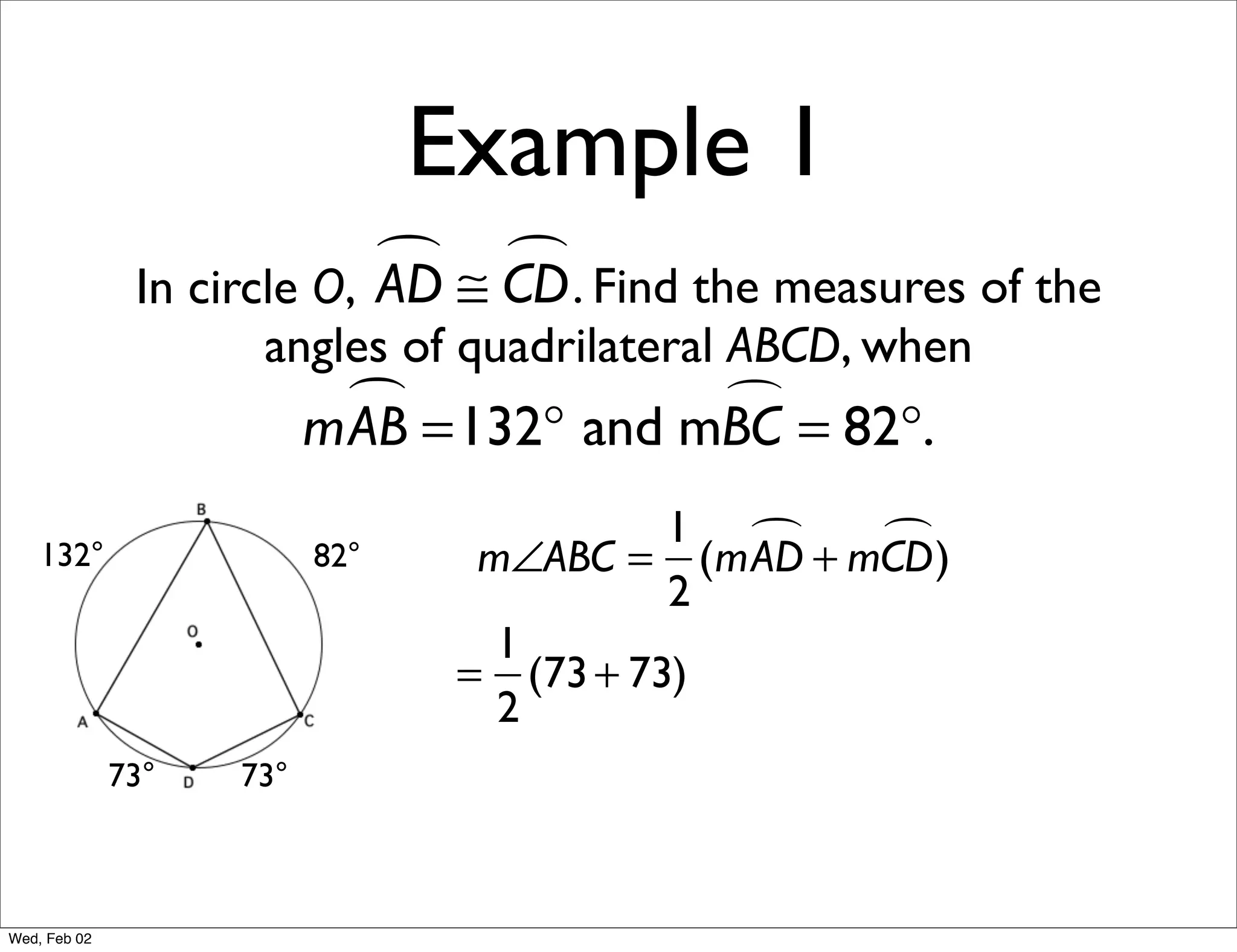
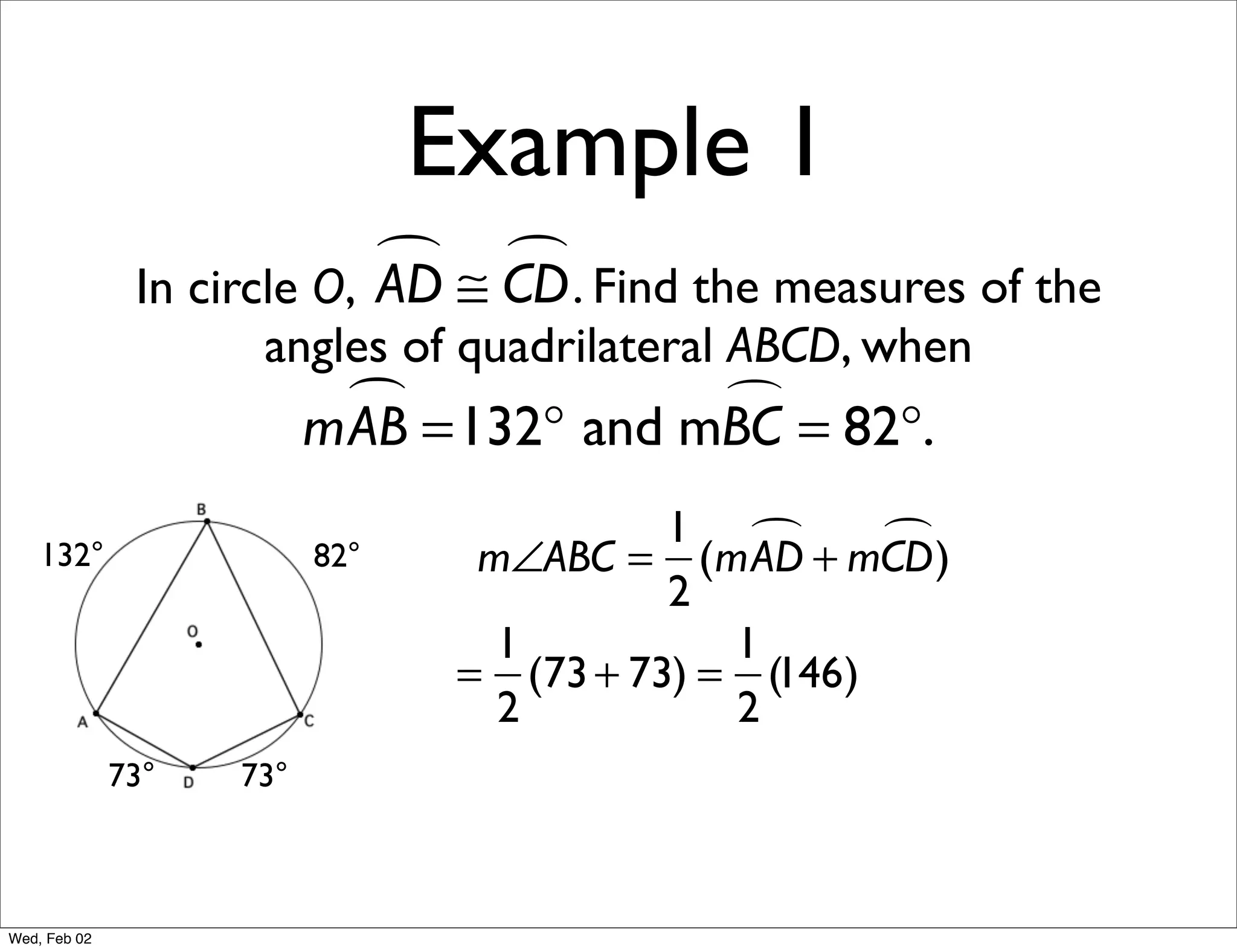
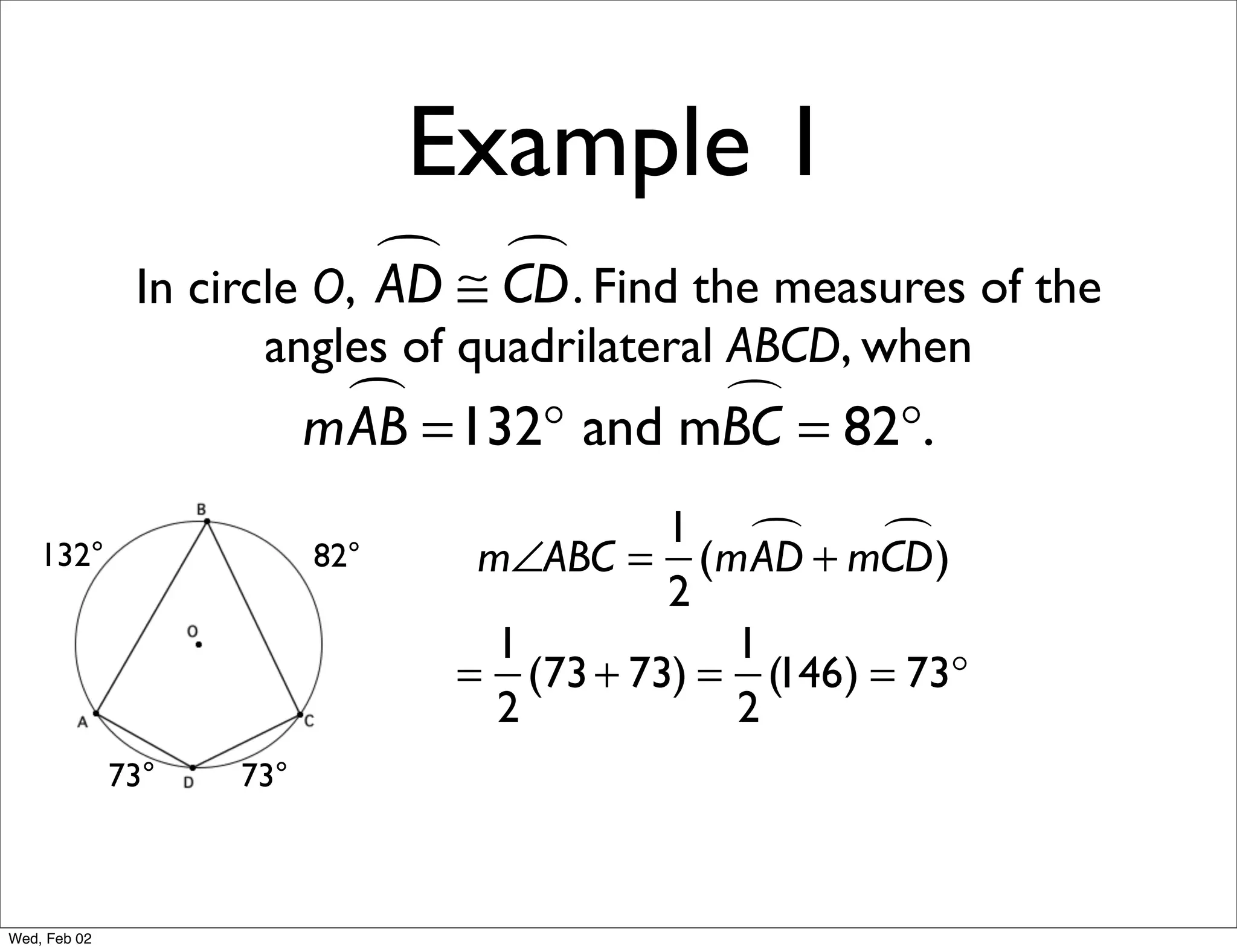
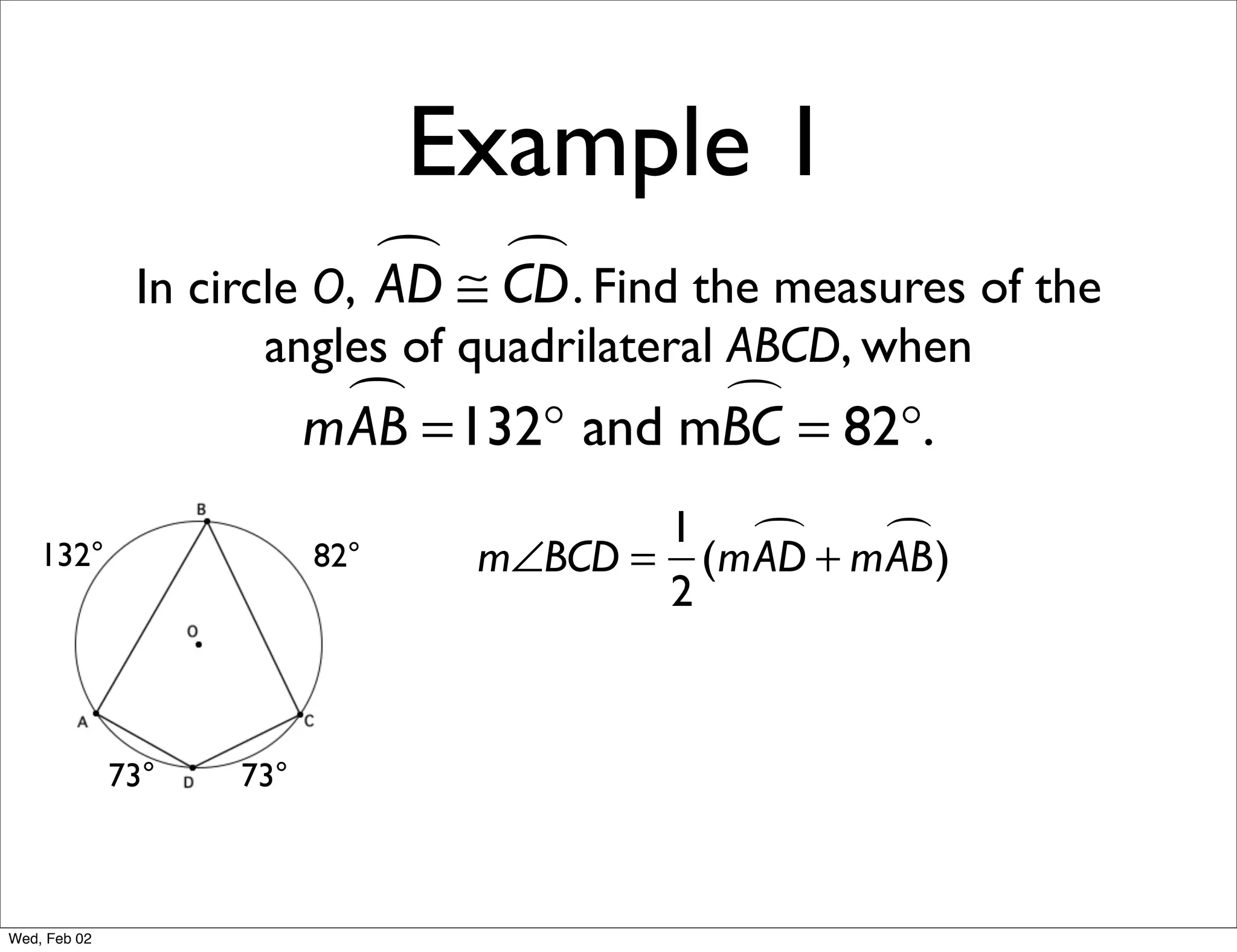
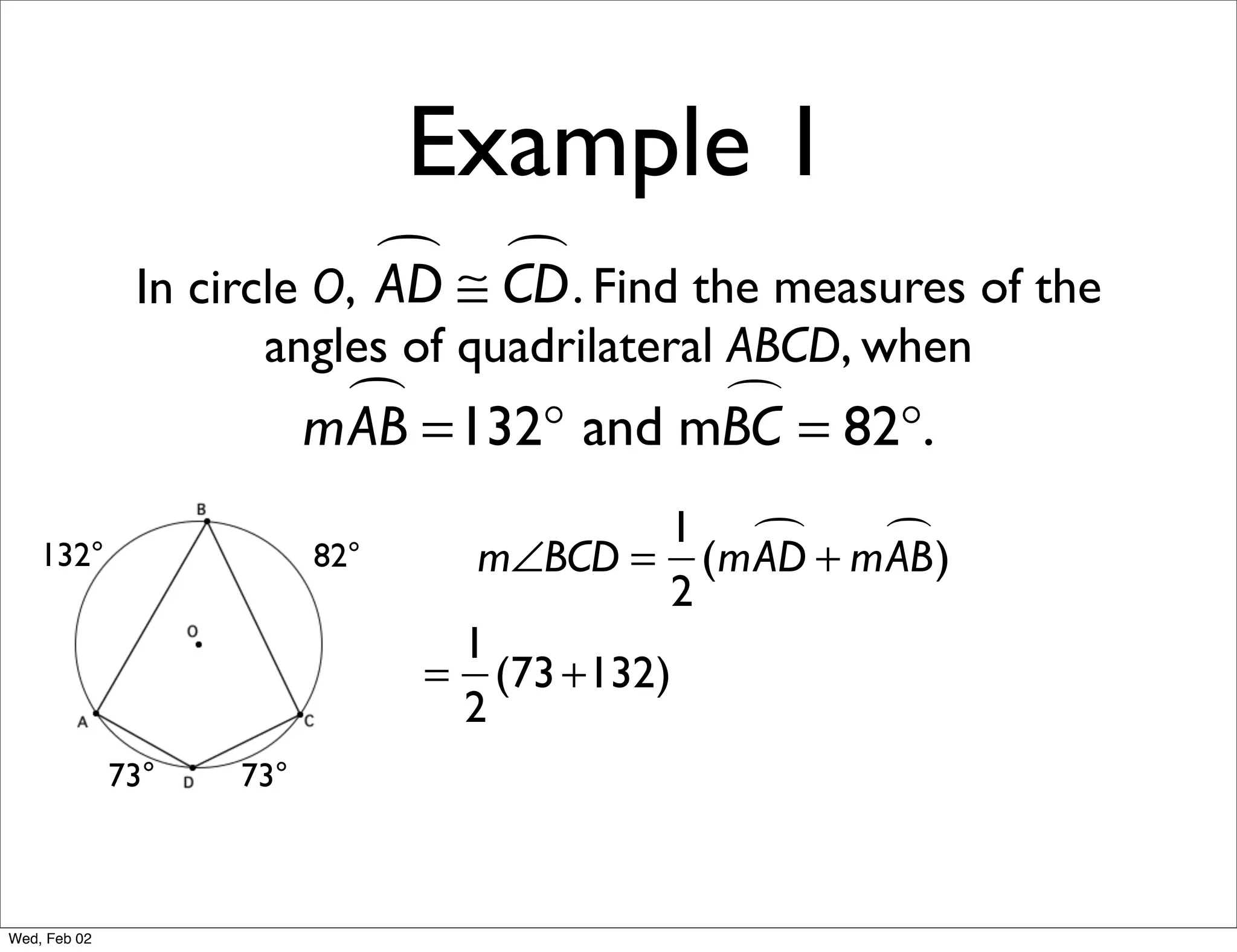
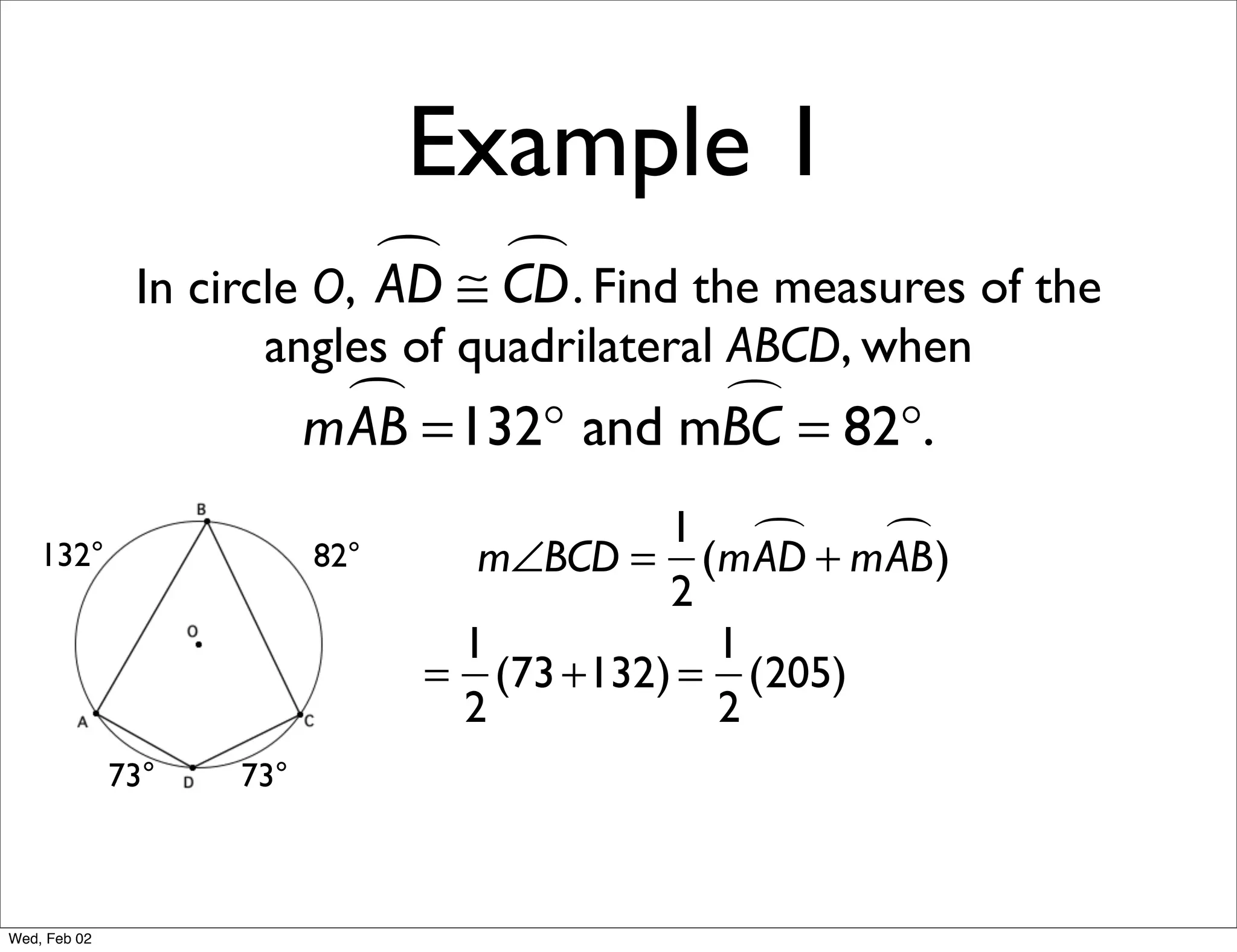
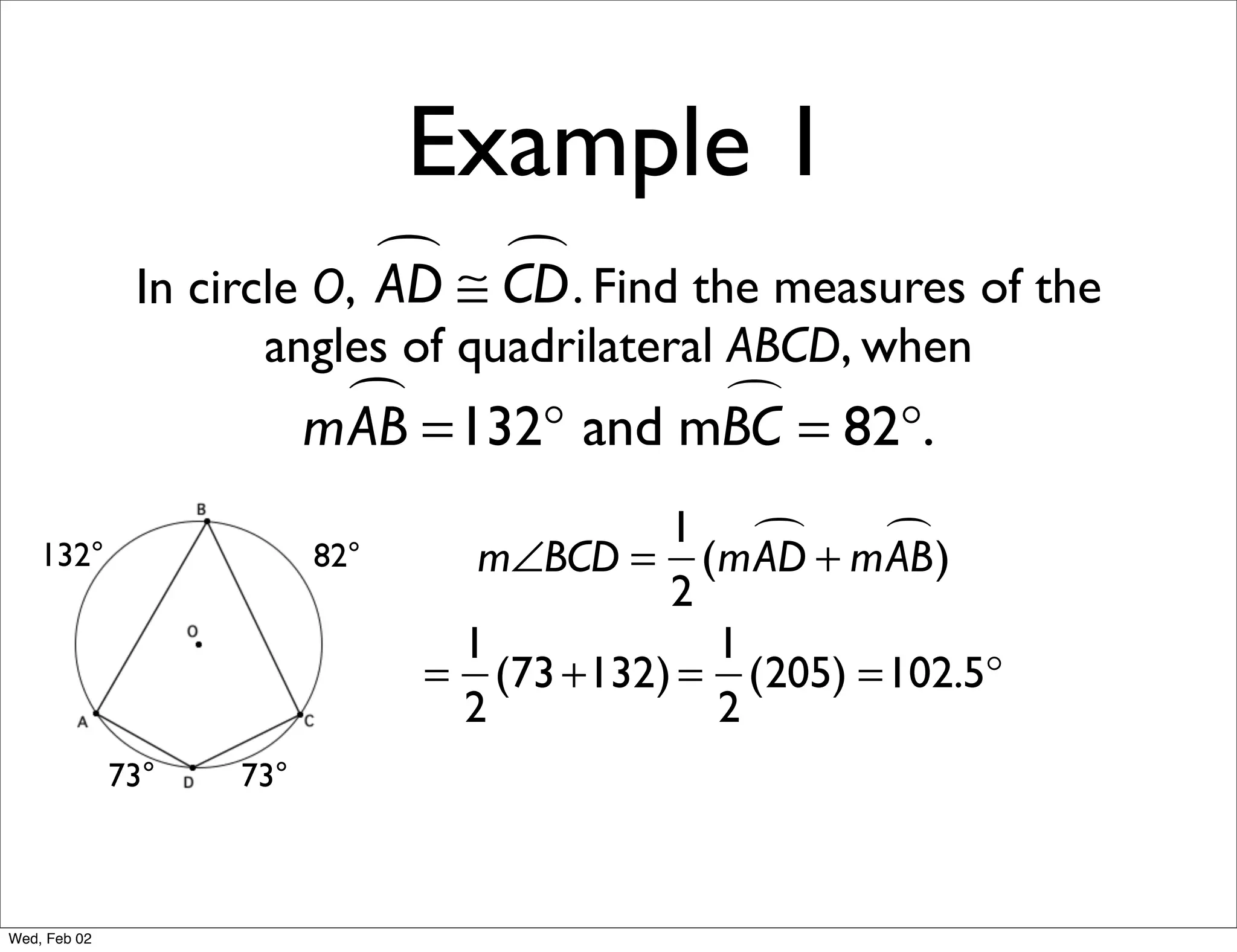
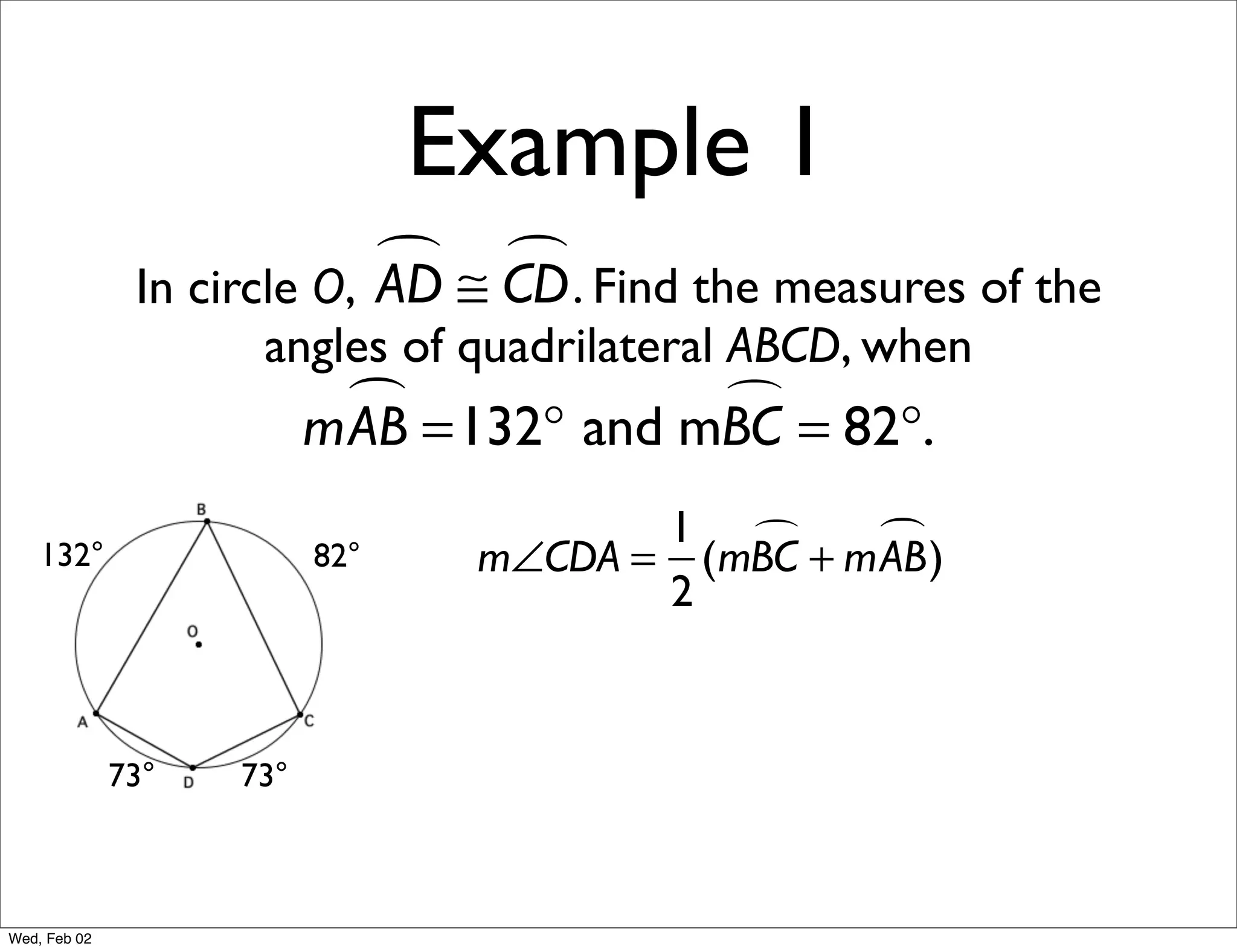
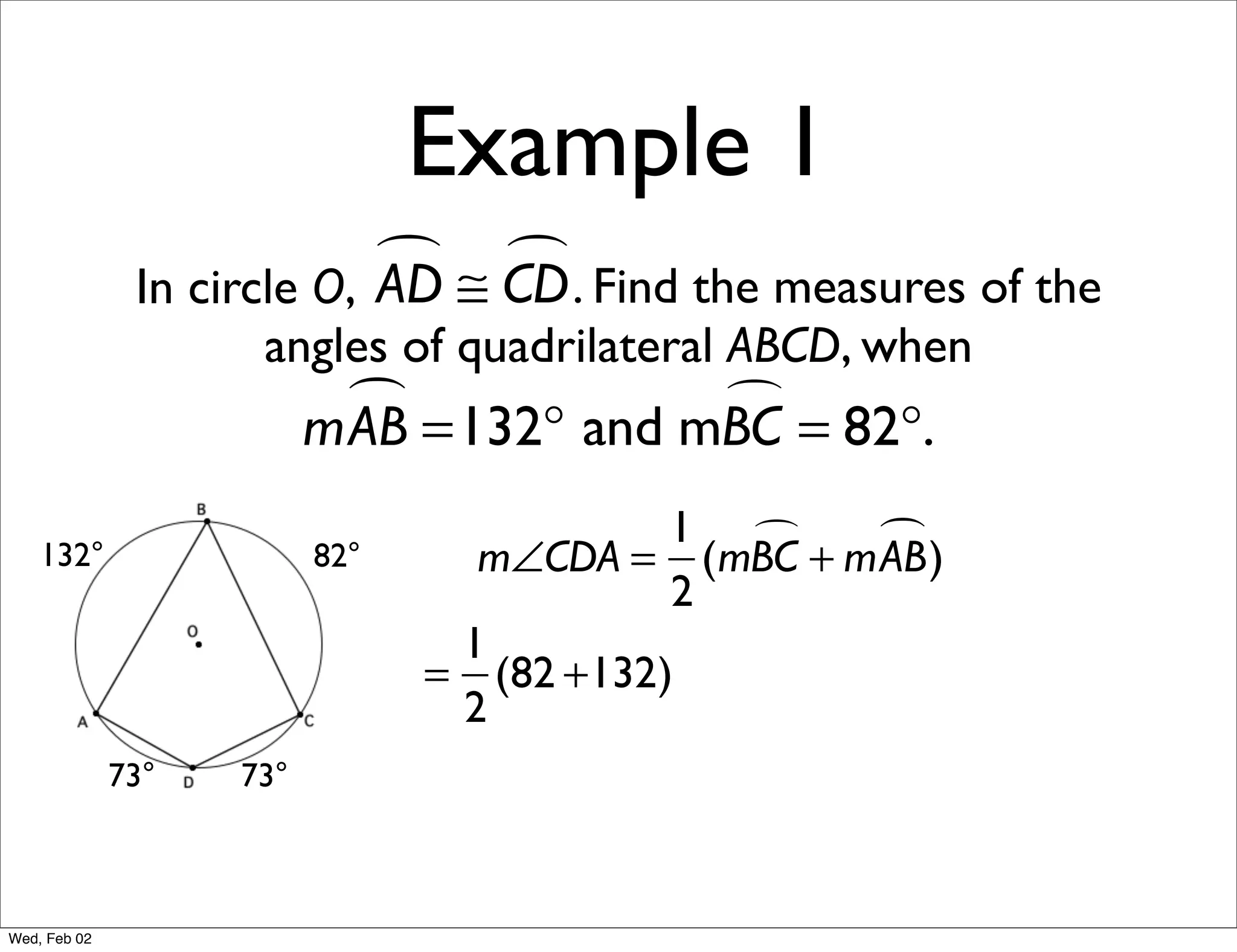
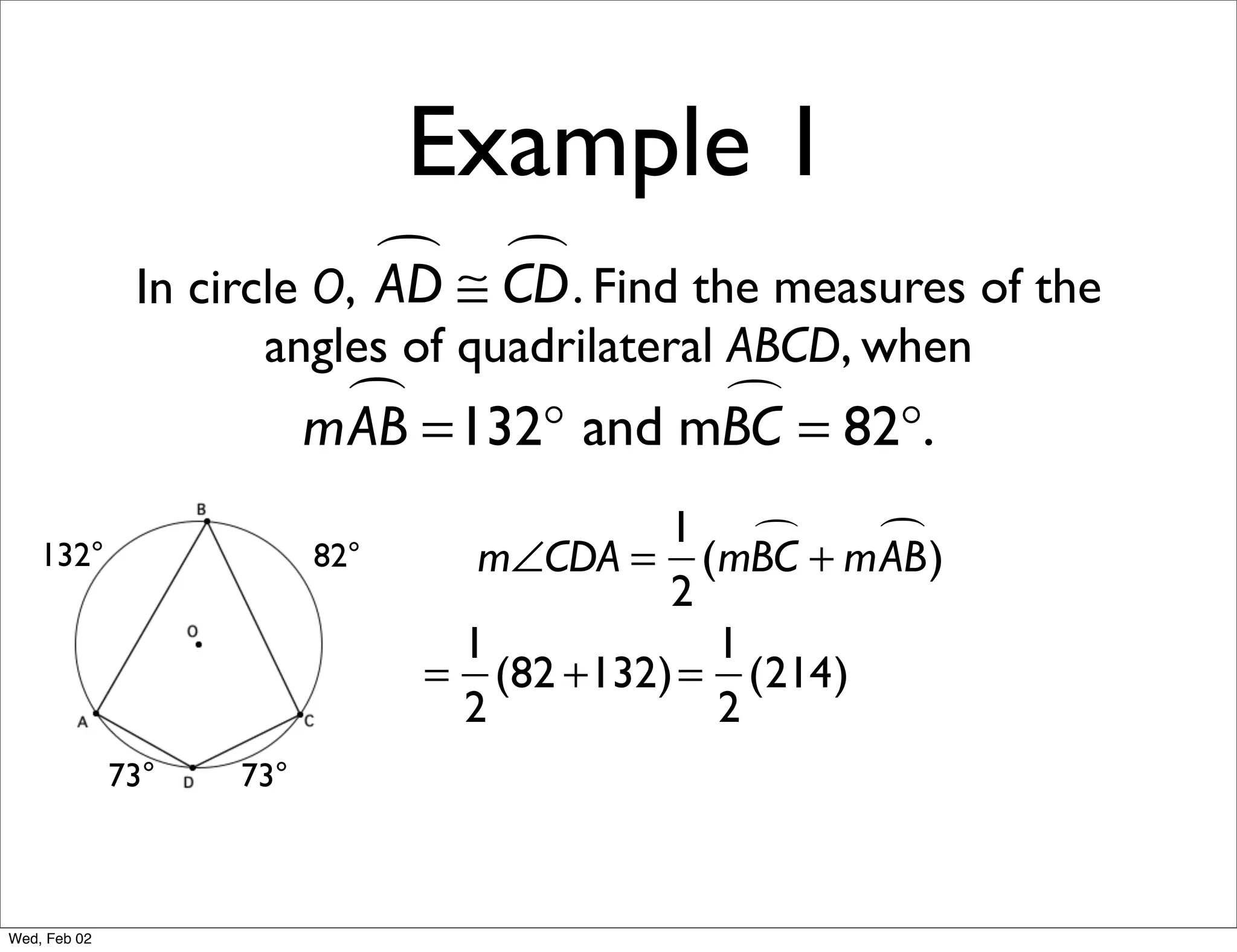
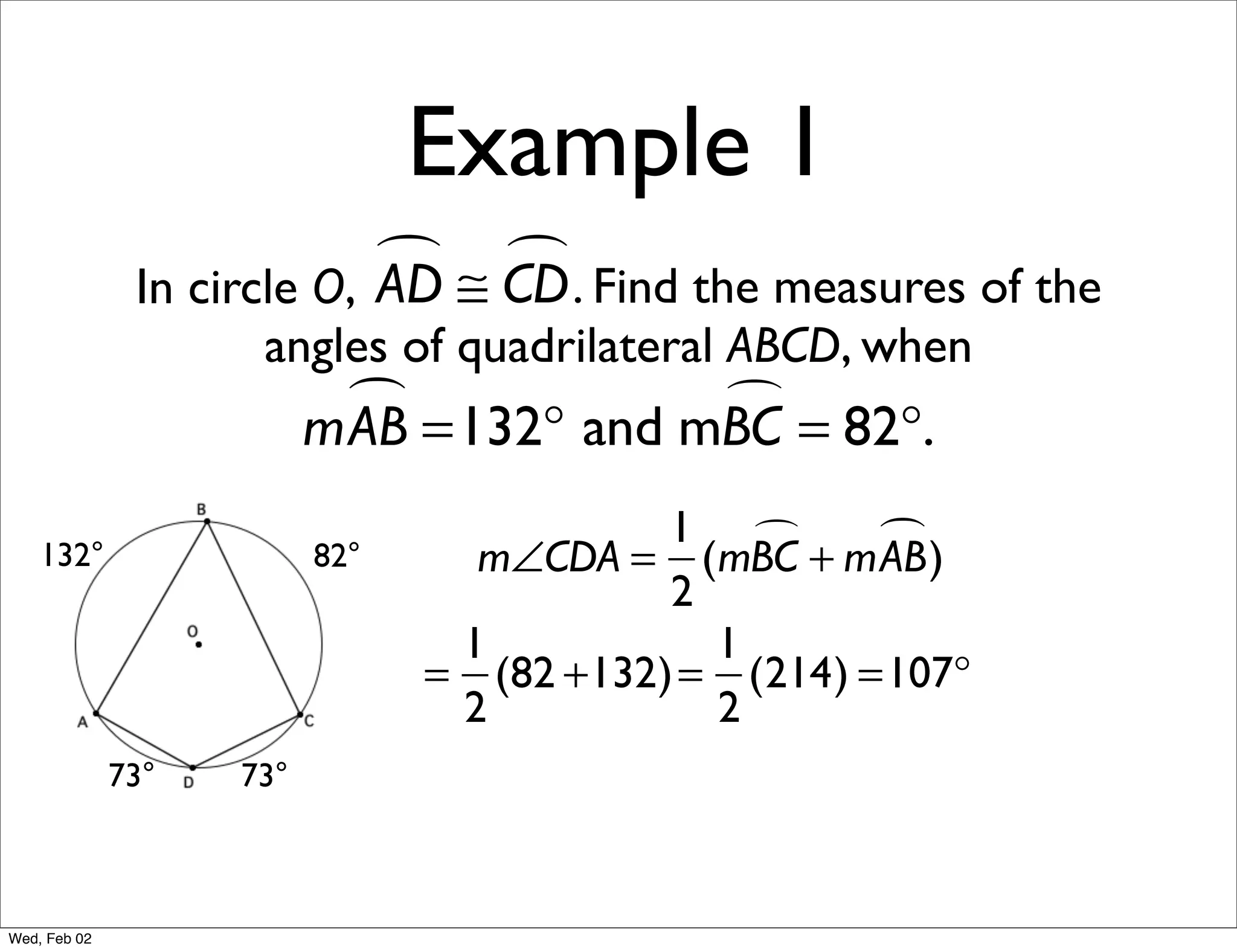
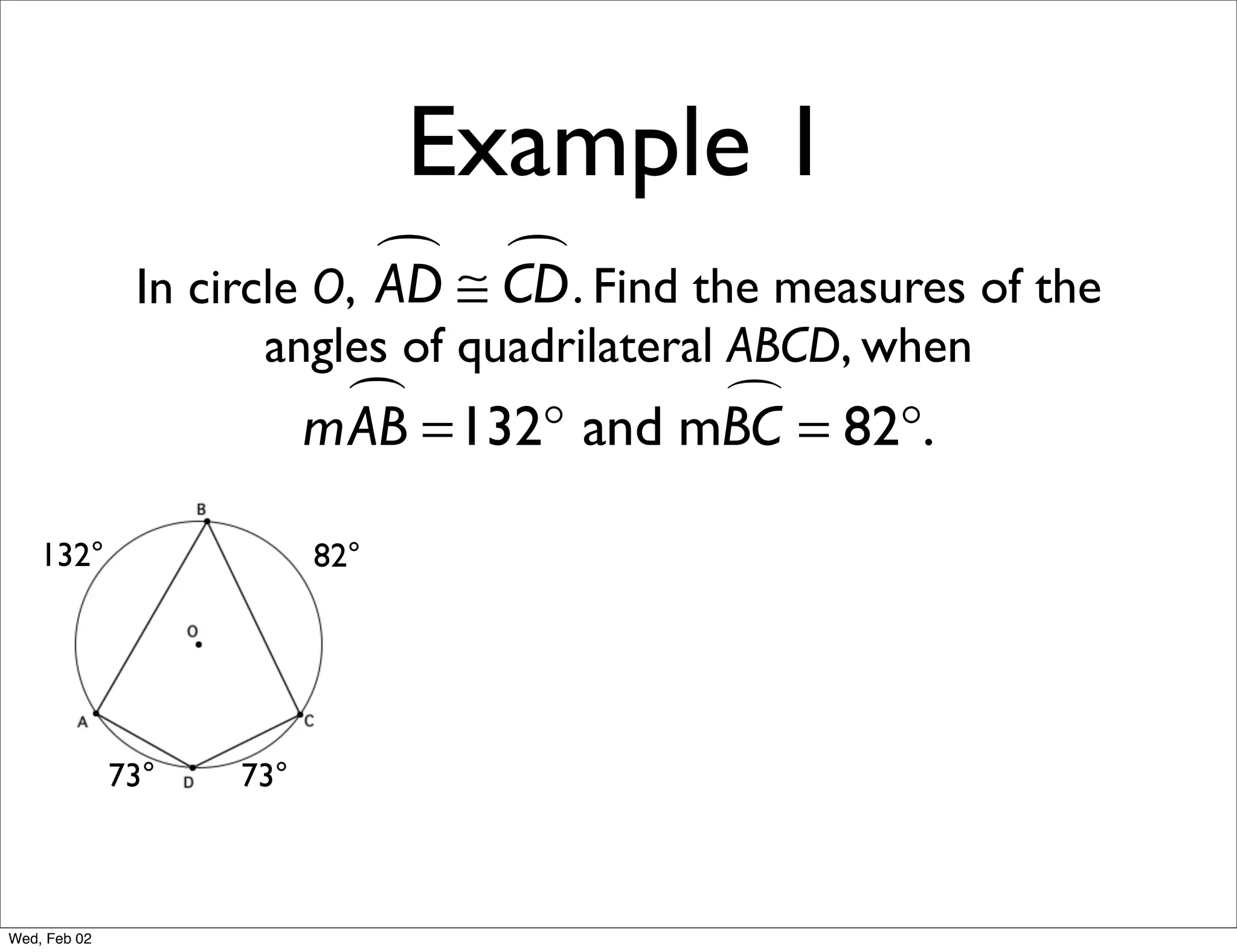
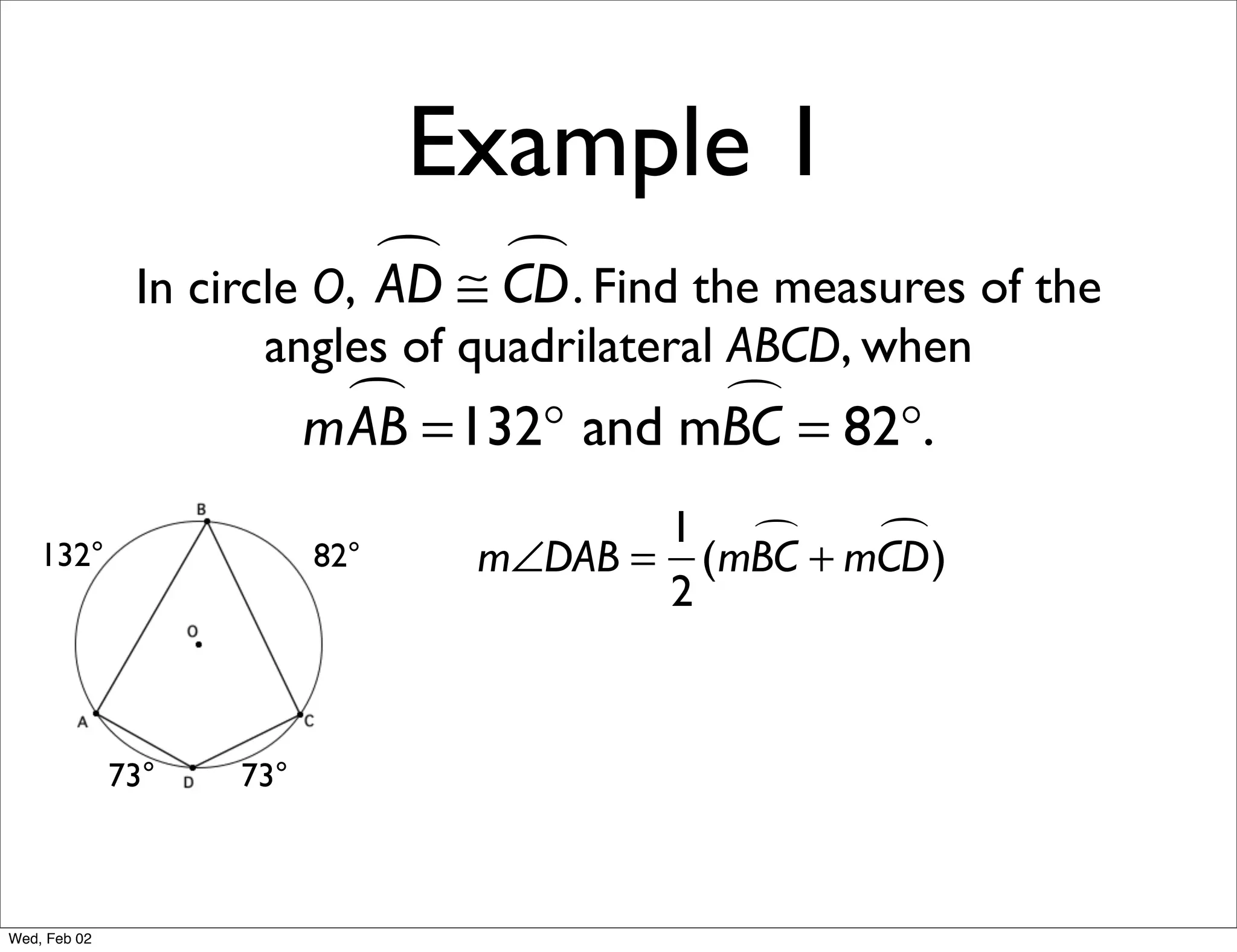
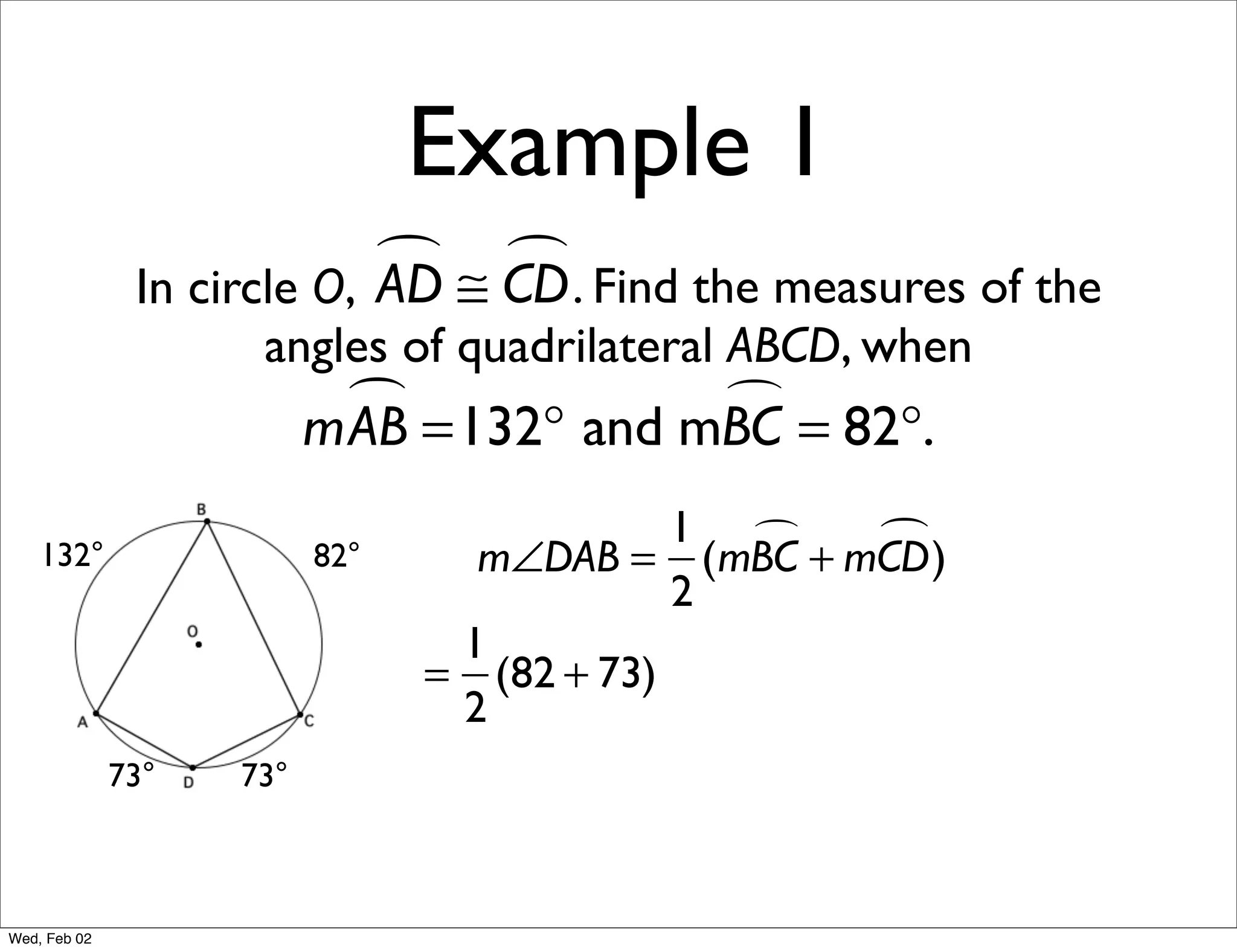
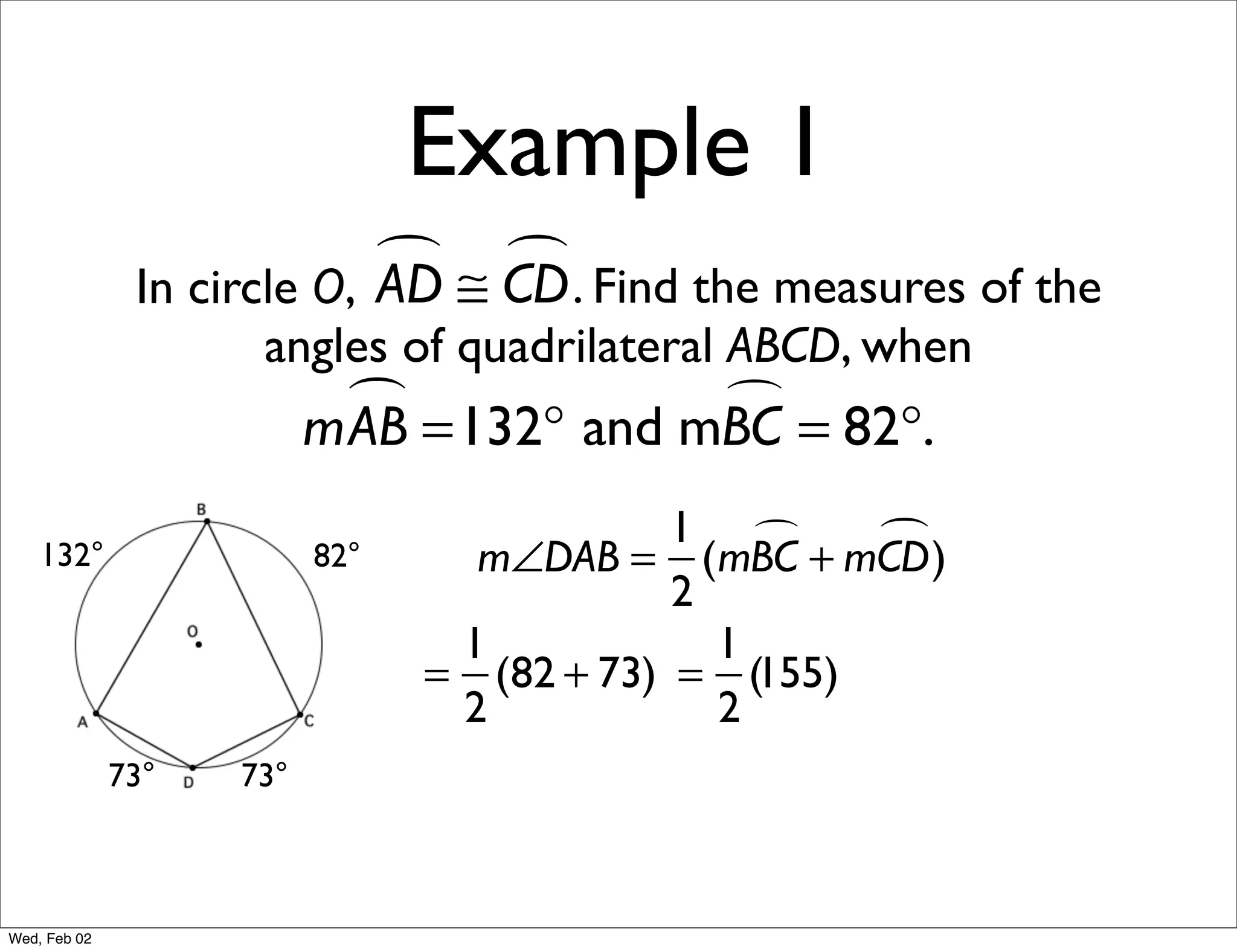
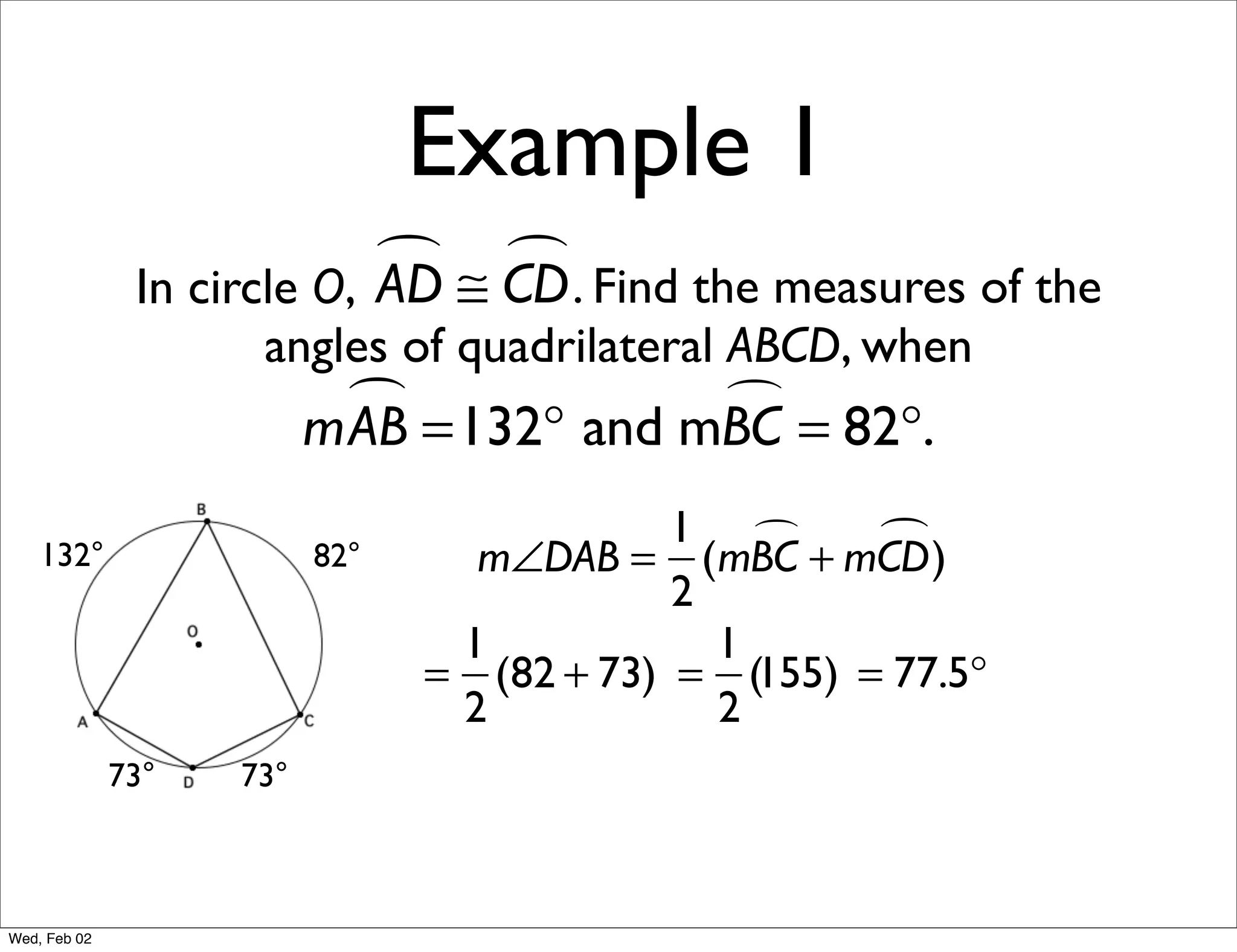
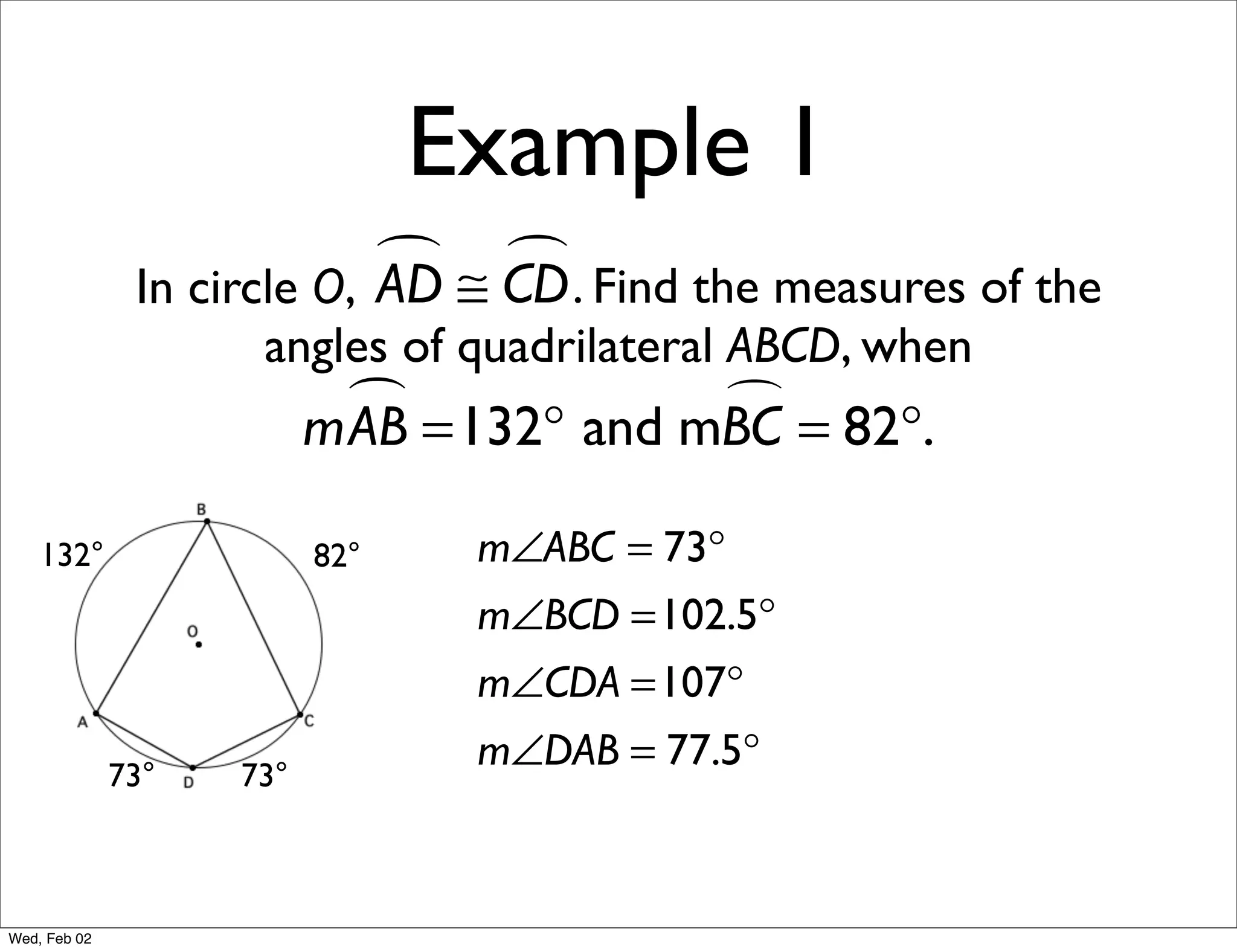
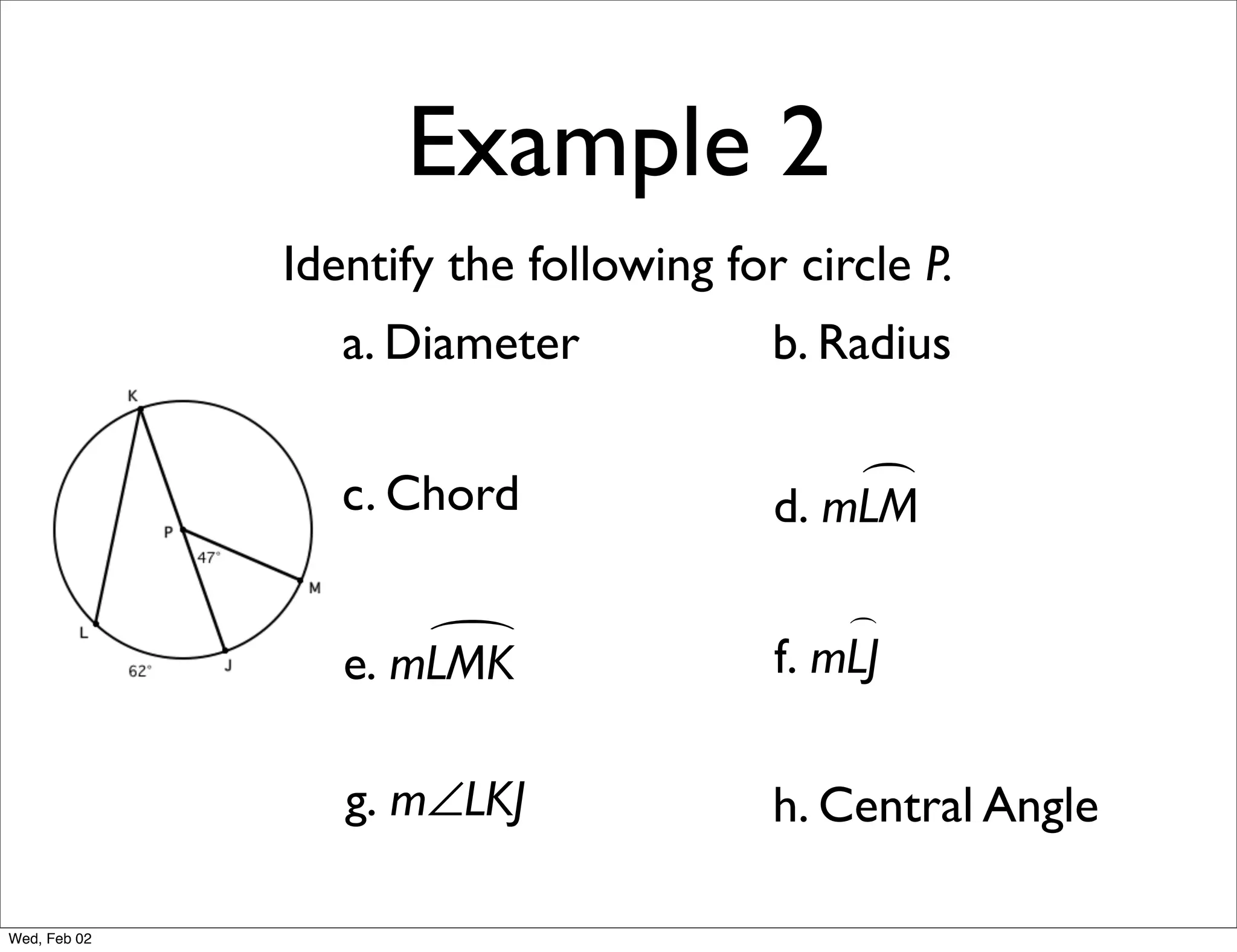
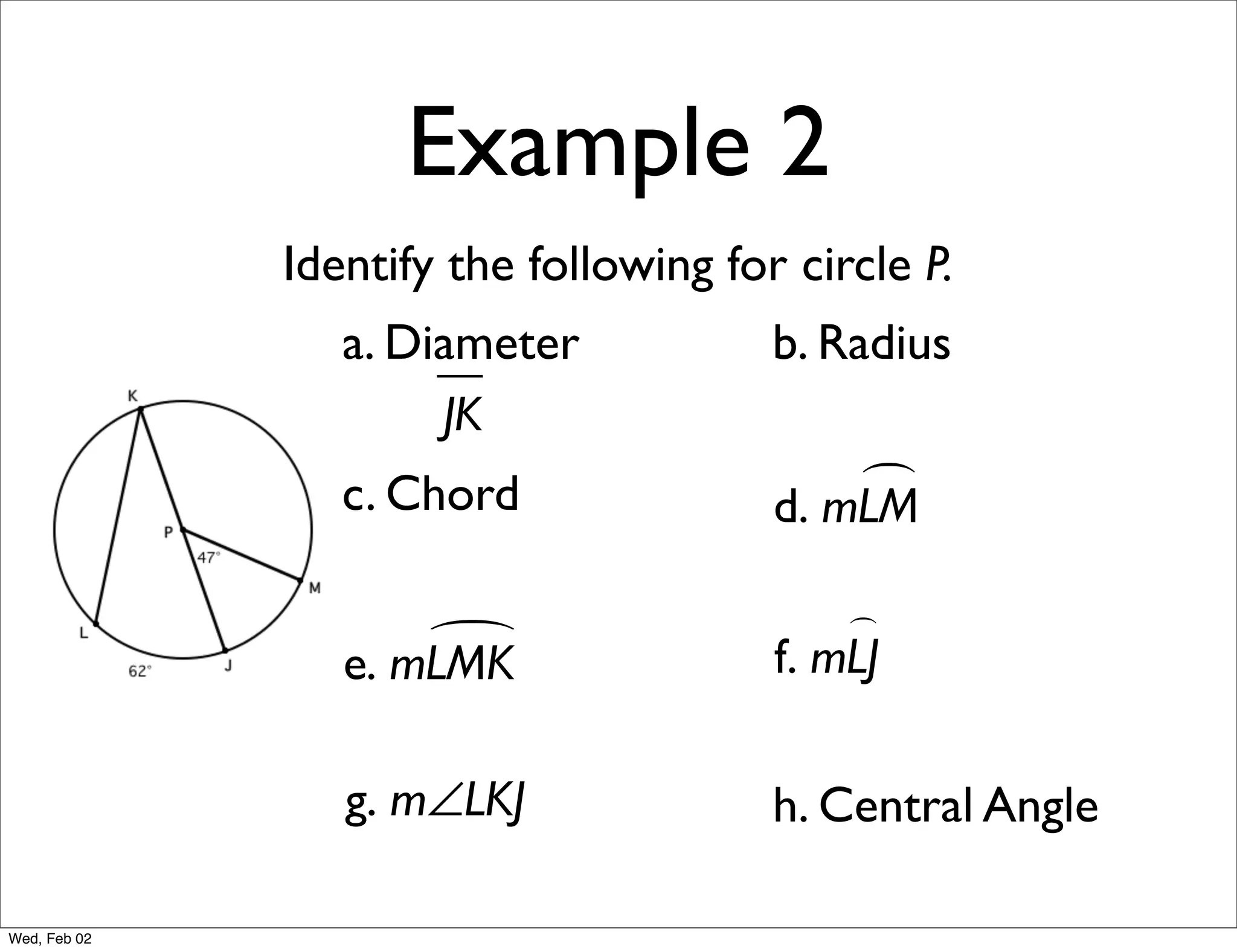
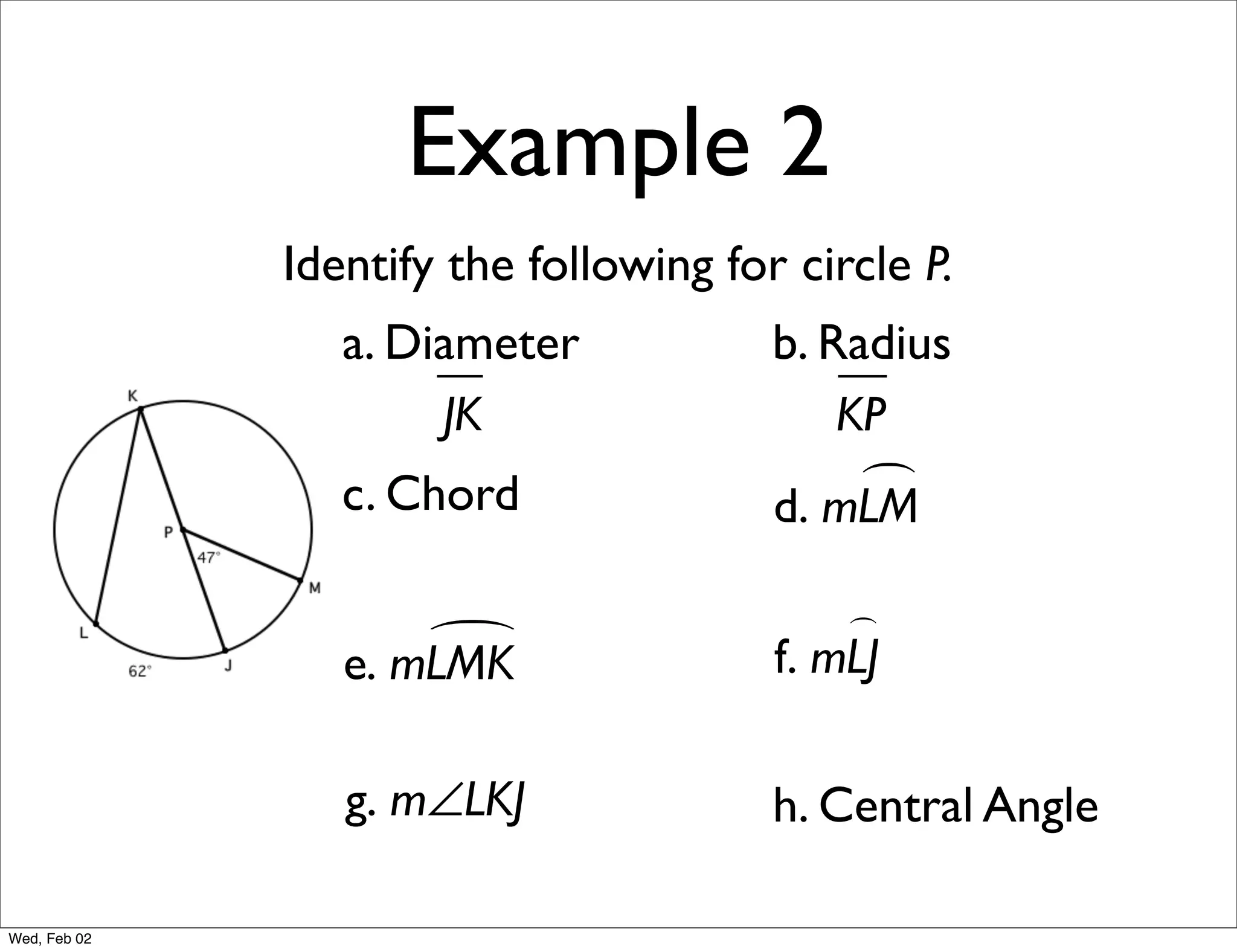
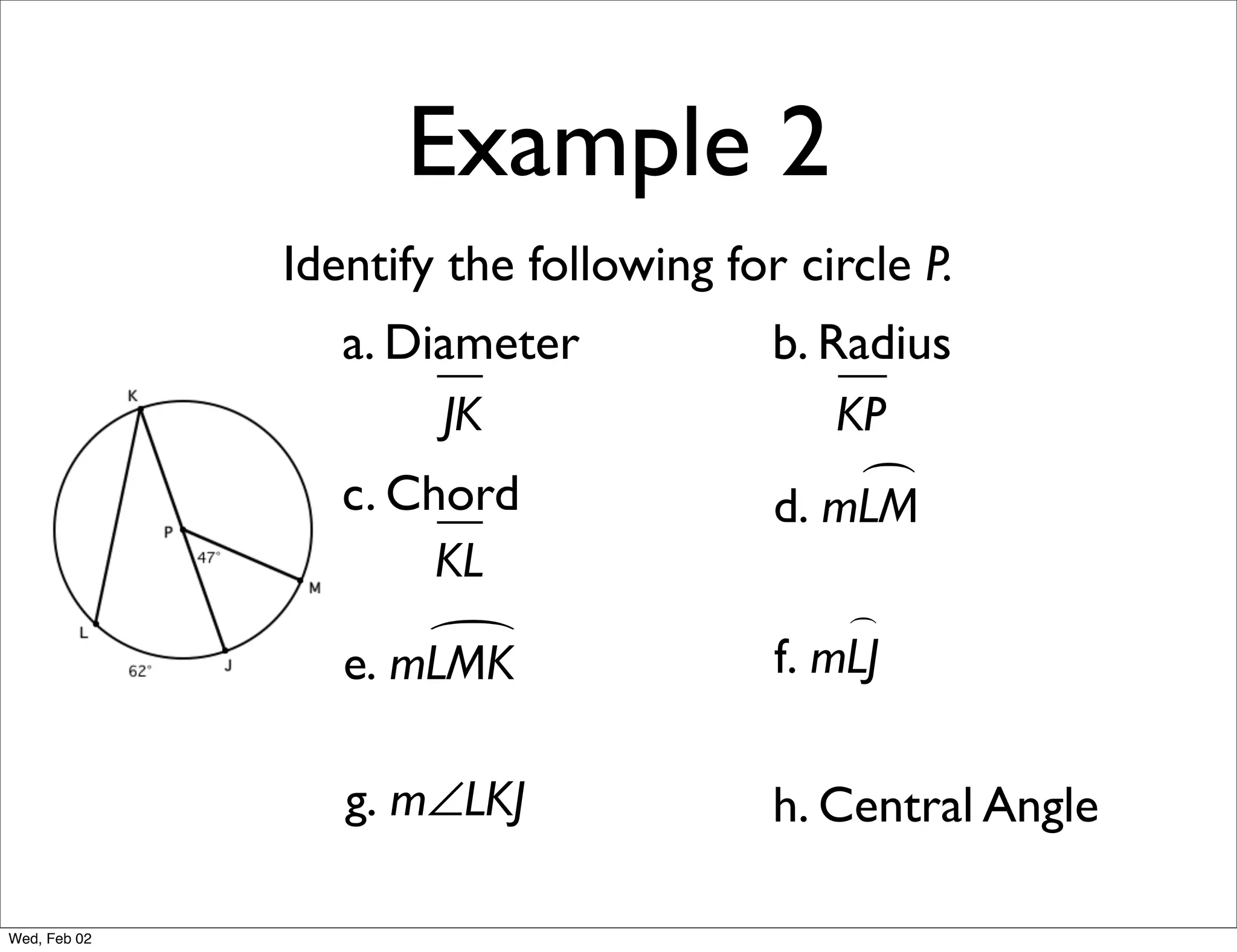
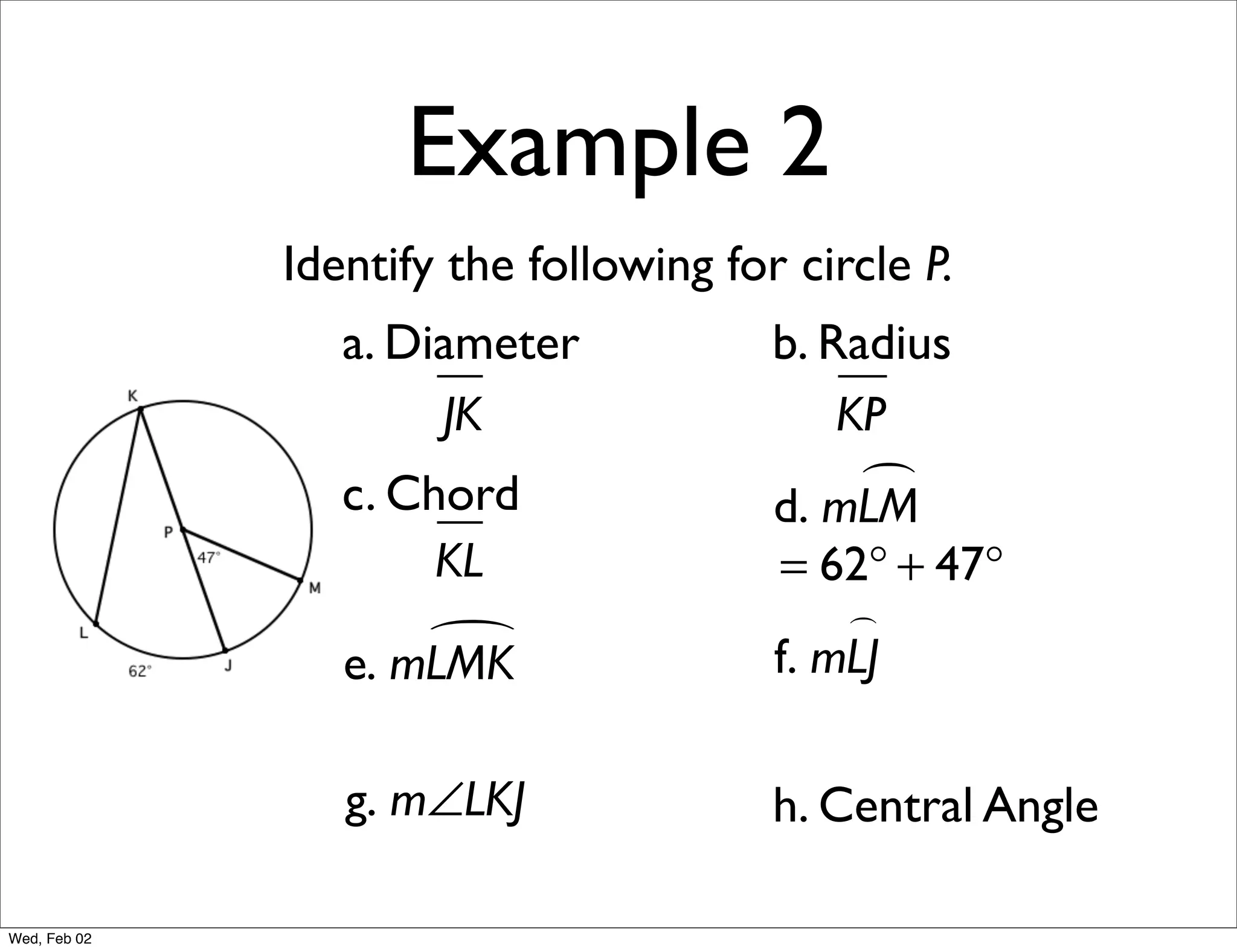
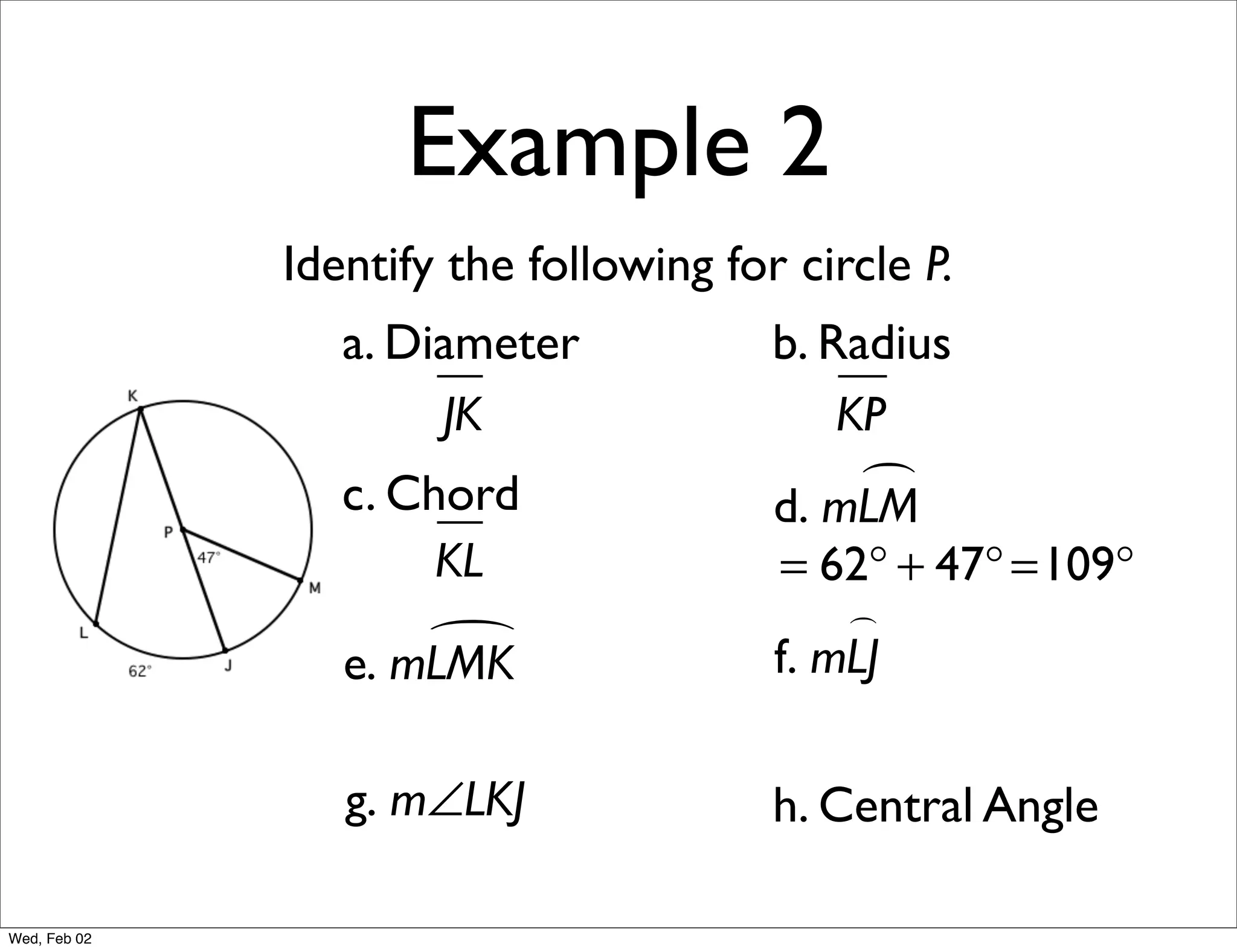
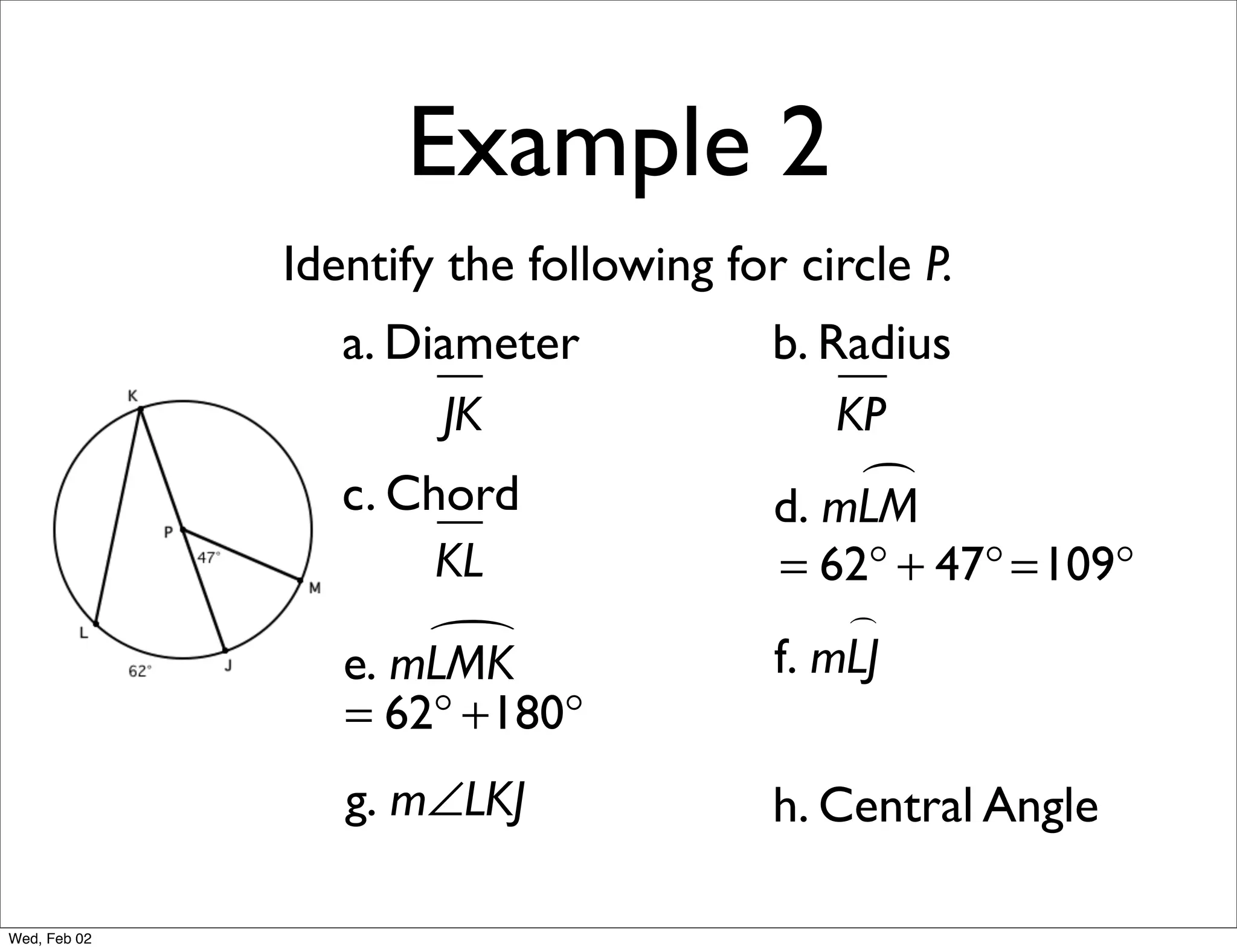
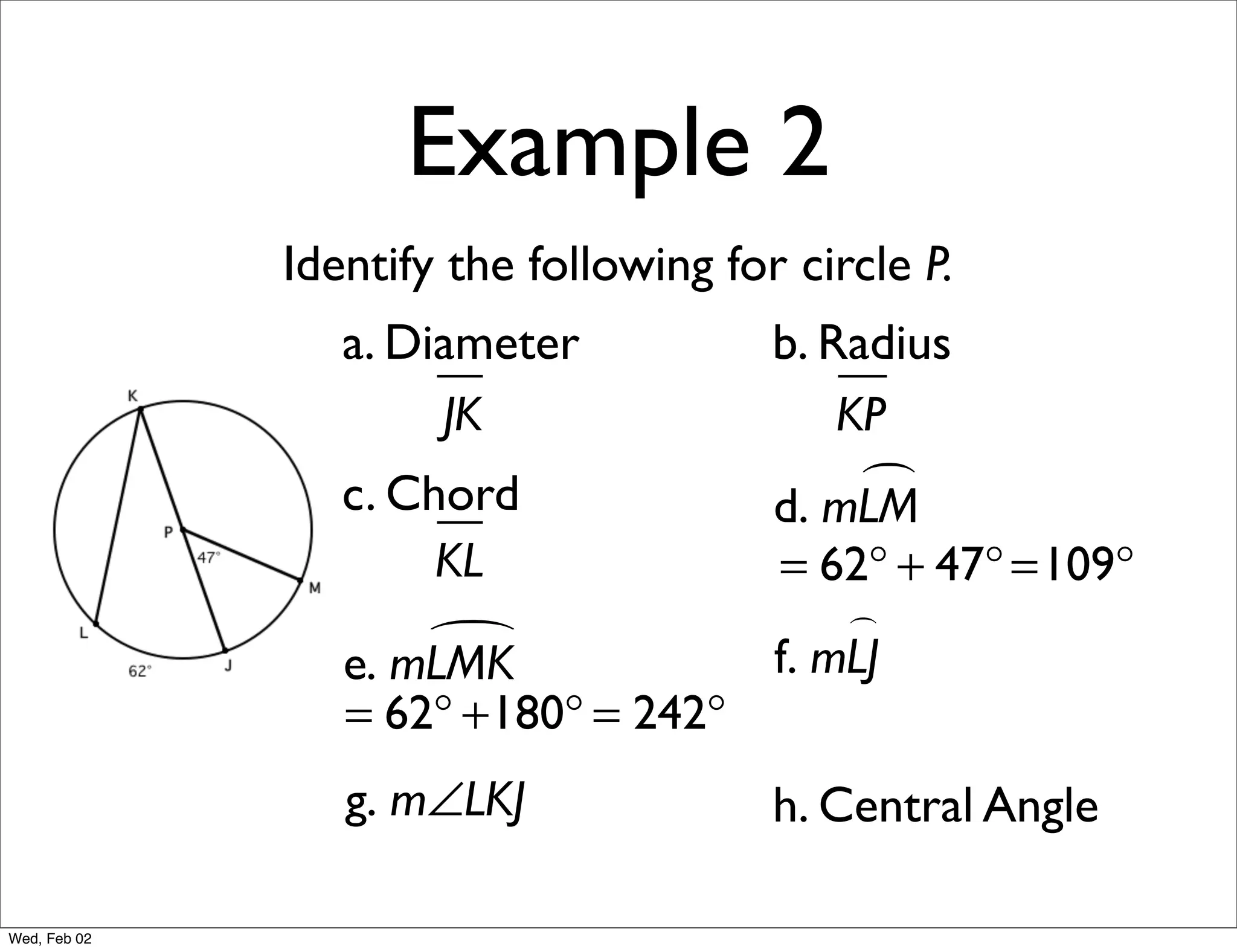
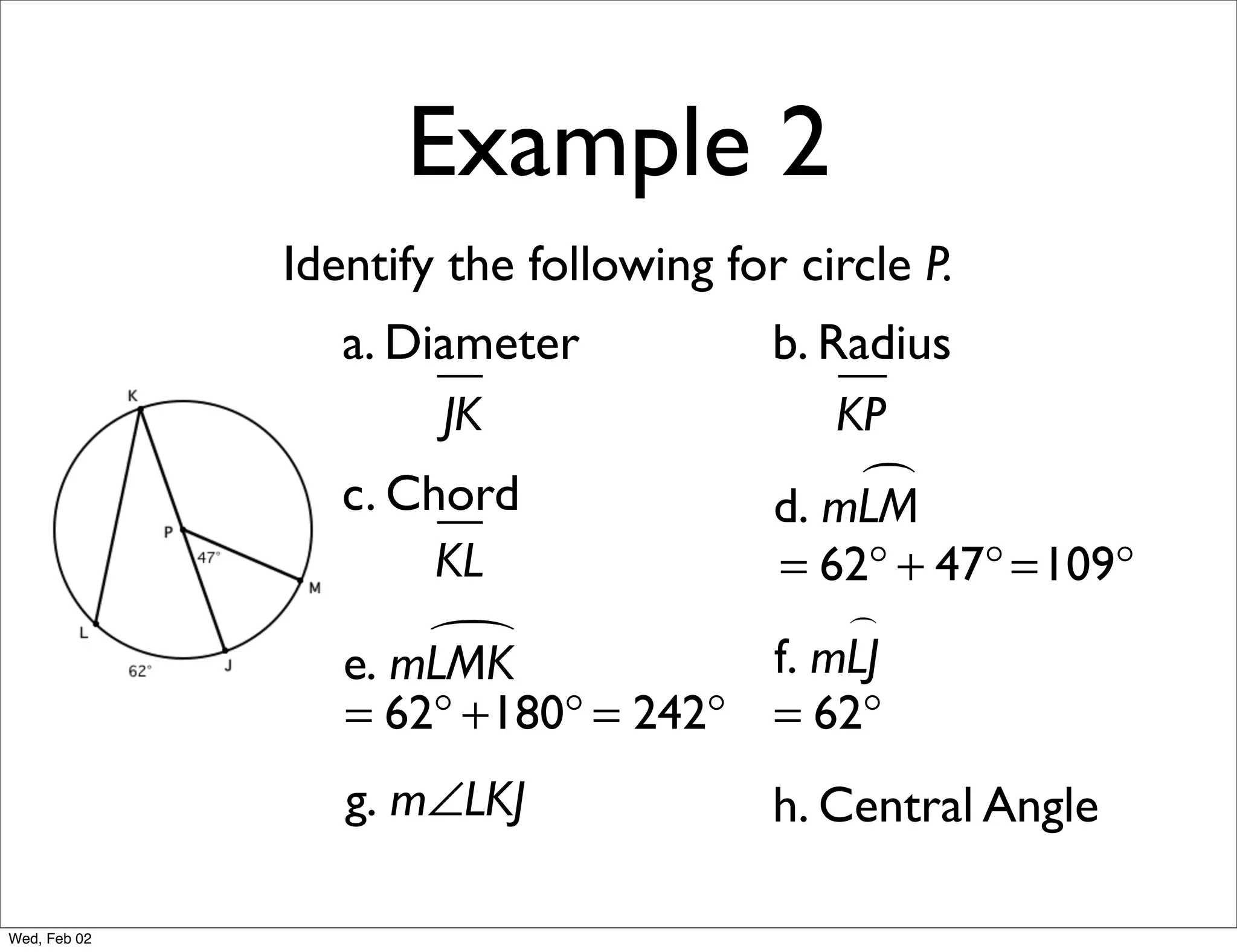
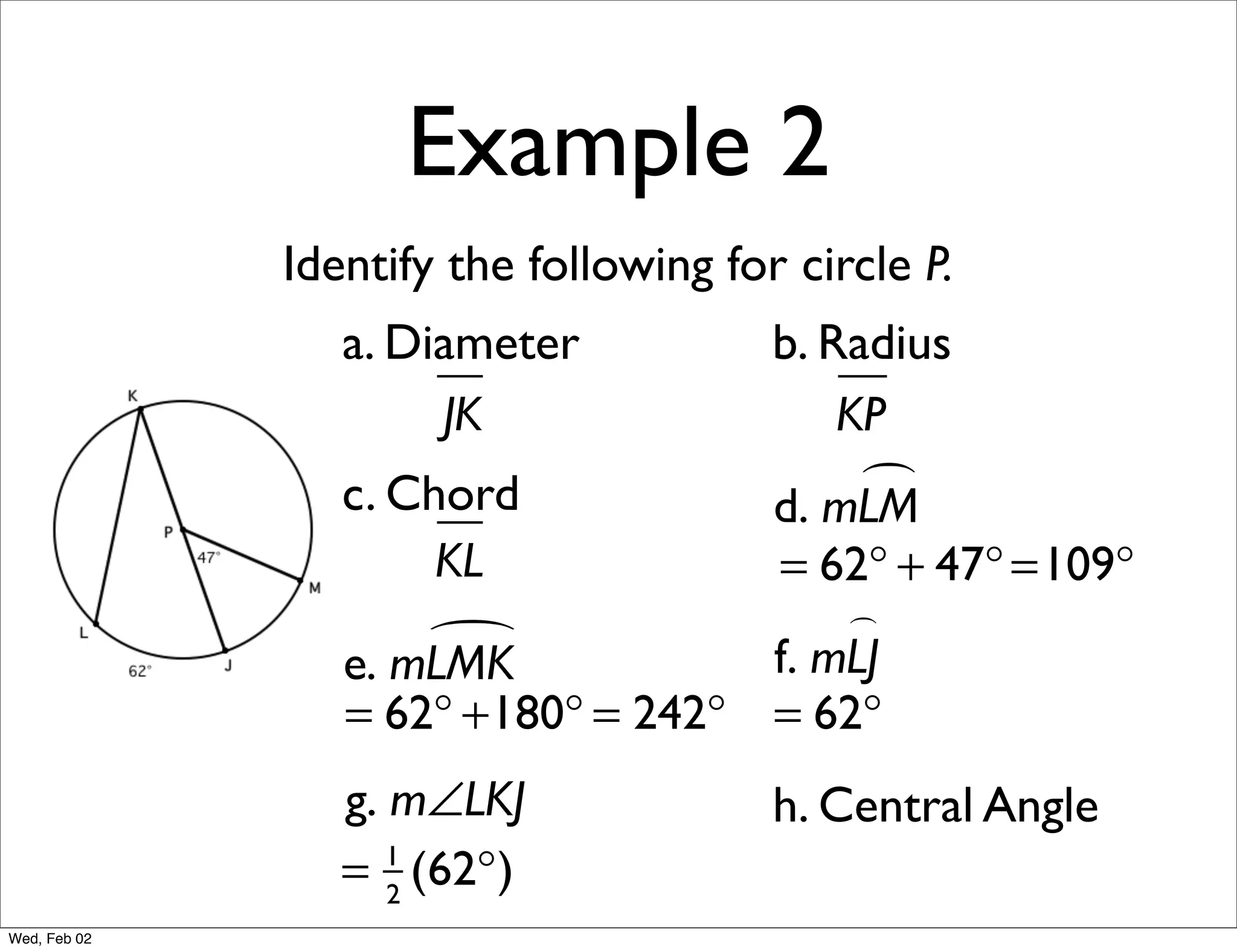
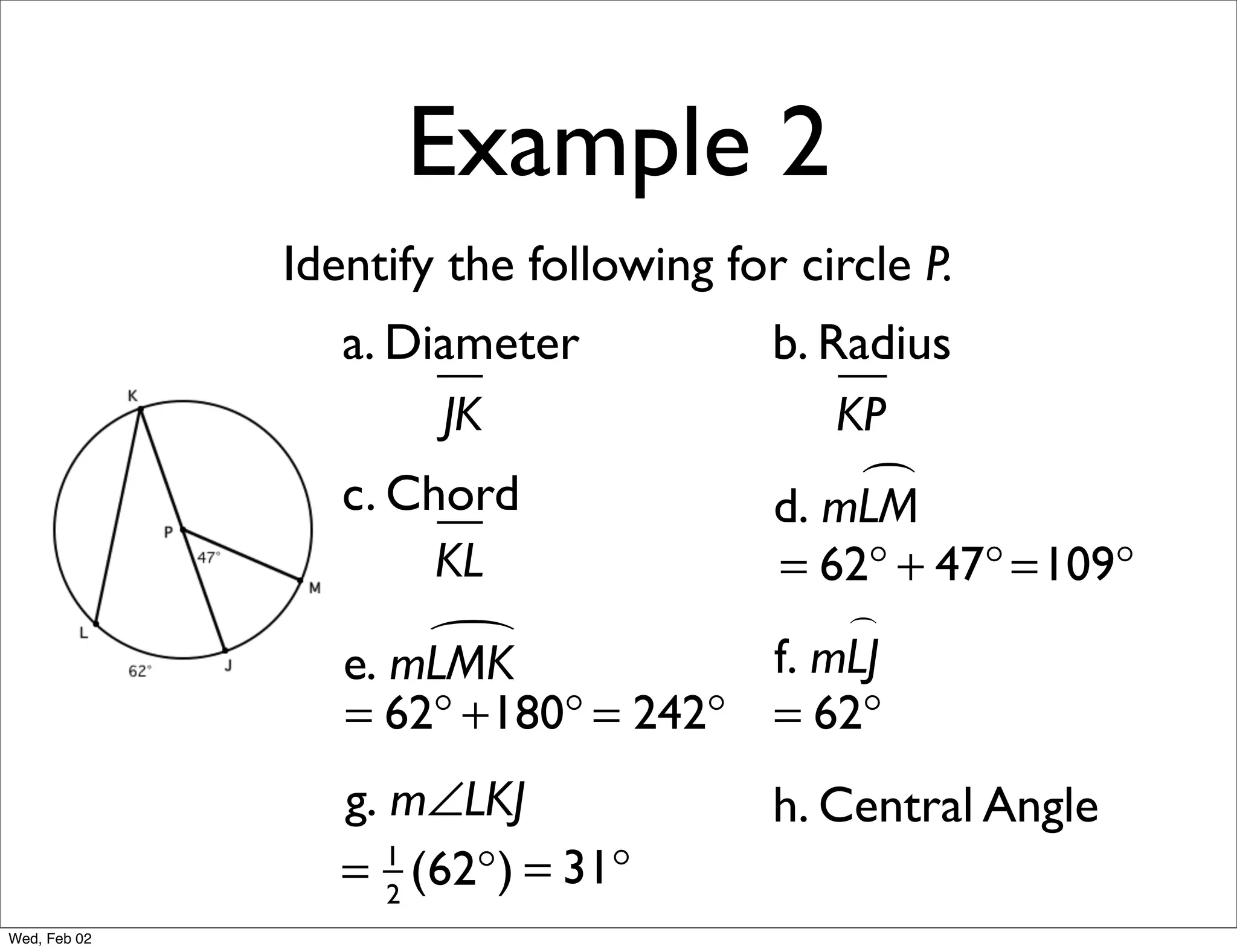
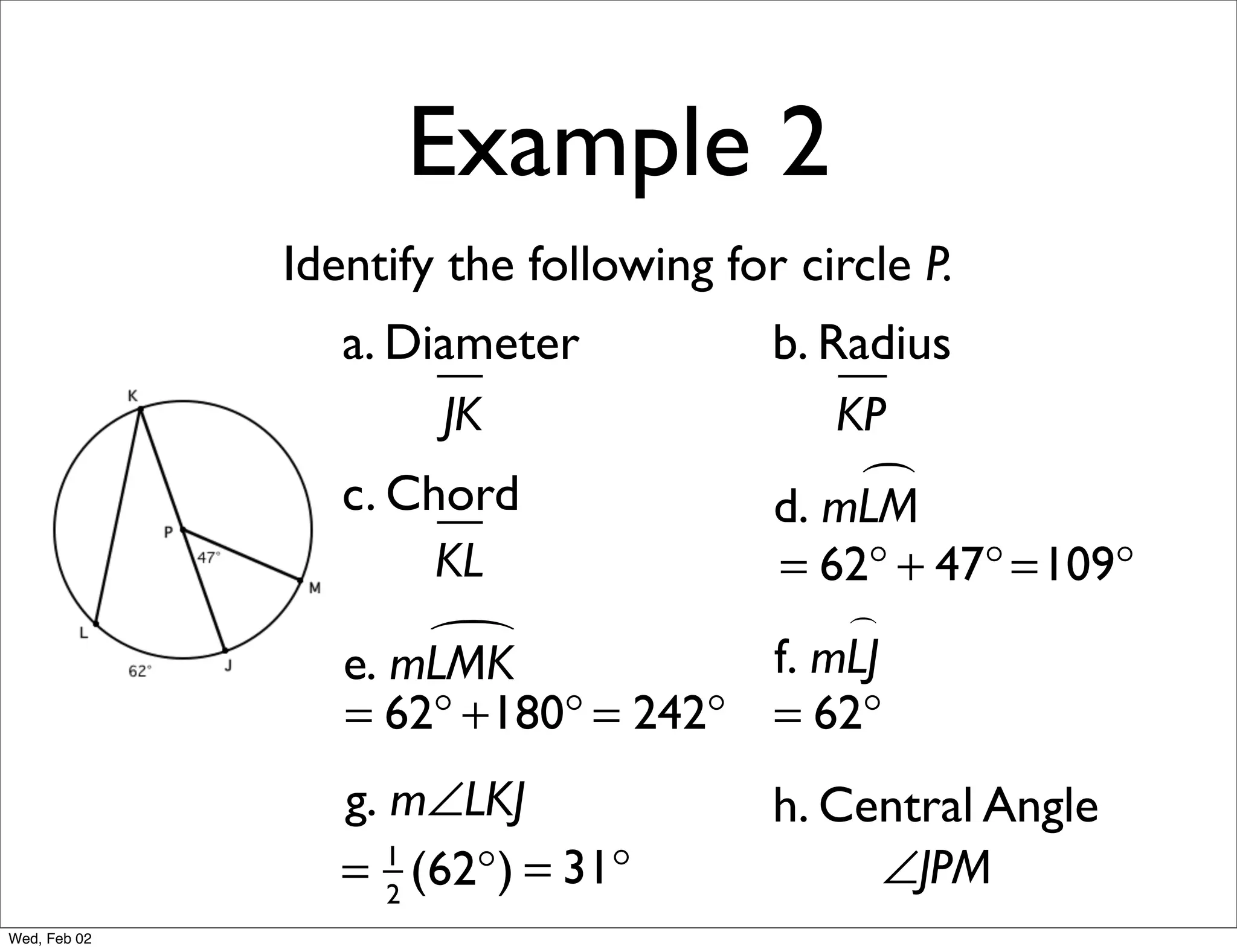
This document provides information about properties of circles. It begins with essential questions about relationships among circle parts and applying circle properties. Next, it defines key circle terms like radius, chord, diameter, and central angle. Examples are then provided to demonstrate using properties to find measures of angles related to circles. The document aims to teach readers about defining features of circles and how to apply circle properties to solve geometric problems.

1. Section 5-8
Properties of Circles
Wed, Feb 02

2. Essential Questions
• What are the relationships among parts of
a circle?
• What are the properties of circles and how
do you apply them?
• Where you’ll see this:
• Market research, food service, art,
recreation, navigation
Wed, Feb 02

3. Vocabulary
1. Circle:
2. Radius:
3. Chord:
4. Diameter:
5. Central Angle:
Wed, Feb 02

4. Vocabulary
1. Circle: All points that are the same distance from a
fixed center point; 360° total
2. Radius:
3. Chord:
4. Diameter:
5. Central Angle:
Wed, Feb 02

5. Vocabulary
1. Circle: All points that are the same distance from a
fixed center point; 360° total
2. Radius: A segment whose endpoints are the center
of a circle and on the circle
3. Chord:
4. Diameter:
5. Central Angle:
Wed, Feb 02

6. Vocabulary
1. Circle: All points that are the same distance from a
fixed center point; 360° total
2. Radius: A segment whose endpoints are the center
of a circle and on the circle
3. Chord: A segment where both endpoints are on the
circle
4. Diameter:
5. Central Angle:
Wed, Feb 02

7. Vocabulary
1. Circle: All points that are the same distance from a
fixed center point; 360° total
2. Radius: A segment whose endpoints are the center
of a circle and on the circle
3. Chord: A segment where both endpoints are on the
circle
4. Diameter: A chord that goes through the center of a
circle
5. Central Angle:
Wed, Feb 02

8. Vocabulary
1. Circle: All points that are the same distance from a
fixed center point; 360° total
2. Radius: A segment whose endpoints are the center
of a circle and on the circle
3. Chord: A segment where both endpoints are on the
circle
4. Diameter: A chord that goes through the center of a
circle
5. Central Angle: An angle where the vertex is the
center of the circle
Wed, Feb 02

9. Vocabulary
6. Arc:
7. Semicircle:
8. Minor Arc:
9. Major Arc:
10. Inscribed Angle:
Wed, Feb 02

10. Vocabulary
6. Arc: A section of the circumference of a circle
7. Semicircle:
8. Minor Arc:
9. Major Arc:
10. Inscribed Angle:
Wed, Feb 02

11. Vocabulary
6. Arc: A section of the circumference of a circle
7. Semicircle: An arc that is half of the circumference;
half a circle
8. Minor Arc:
9. Major Arc:
10. Inscribed Angle:
Wed, Feb 02

12. Vocabulary
6. Arc: A section of the circumference of a circle
7. Semicircle: An arc that is half of the circumference;
half a circle
8. Minor Arc: An arc that is less than half the
circumference; same measure as the central angle
9. Major Arc:
10. Inscribed Angle:
Wed, Feb 02

13. Vocabulary
6. Arc: A section of the circumference of a circle
7. Semicircle: An arc that is half of the circumference;
half a circle
8. Minor Arc: An arc that is less than half the
circumference; same measure as the central angle
9. Major Arc: An arc that is more than half the
circumference
10. Inscribed Angle:
Wed, Feb 02

14. Vocabulary
6. Arc: A section of the circumference of a circle
7. Semicircle: An arc that is half of the circumference;
half a circle
8. Minor Arc: An arc that is less than half the
circumference; same measure as the central angle
9. Major Arc: An arc that is more than half the
circumference
10. Inscribed Angle: An angle whose vertex is on the
circle and whose sides are chords of the circle; half
the measure of the arc it contains
Wed, Feb 02

15. Circle
Wed, Feb 02

16. Radius
Wed, Feb 02

17. Chord
Wed, Feb 02

18. Diameter
Wed, Feb 02

19. Central Angle
Wed, Feb 02

20. Arc
Wed, Feb 02

21. Semicircle
Wed, Feb 02

22. Minor Arc
Wed, Feb 02

23. Major Arc
Wed, Feb 02

24. Inscribed Angle
Wed, Feb 02

25. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
Wed, Feb 02

26. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
132°
Wed, Feb 02

27. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
132° 82°
Wed, Feb 02

28. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
132° 82°
x°
Wed, Feb 02

29. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
132° 82°
x° x°
Wed, Feb 02

30. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
x + x +132 + 82 = 360
132° 82°
x° x°
Wed, Feb 02

31. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
x + x +132 + 82 = 360
132° 82°
2x + 214 = 360
x° x°
Wed, Feb 02

32. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
x + x +132 + 82 = 360
132° 82°
2x + 214 = 360
−214 −214
x° x°
Wed, Feb 02

33. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
x + x +132 + 82 = 360
132° 82°
2x + 214 = 360
−214 −214
2x =146
x° x°
Wed, Feb 02

34. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
x + x +132 + 82 = 360
132° 82°
2x + 214 = 360
−214 −214
2x =146
2 2
x° x°
Wed, Feb 02

35. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
x + x +132 + 82 = 360
132° 82°
2x + 214 = 360
−214 −214
2x =146
2 2
x° x° x = 73
Wed, Feb 02

36. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
x + x +132 + 82 = 360
132° 82°
2x + 214 = 360
−214 −214
2x =146
2 2
73° 73° x = 73
Wed, Feb 02

37. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
132° 82°
73° 73°
Wed, Feb 02

38. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠ABC = (mAD + mCD
2
73° 73°
Wed, Feb 02

39. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠ABC = (mAD + mCD
2
1
= (73 + 73)
2
73° 73°
Wed, Feb 02

40. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠ABC = (mAD + mCD
2
1 1
= (73 + 73) = (146)
2 2
73° 73°
Wed, Feb 02

41. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠ABC = (mAD + mCD
2
1 1
= (73 + 73) = (146) = 73°
2 2
73° 73°
Wed, Feb 02

42. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
132° 82°
73° 73°
Wed, Feb 02

43. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠BCD = (mAD + mAB
2
73° 73°
Wed, Feb 02

44. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠BCD = (mAD + mAB
2
1
= (73 +132)
2
73° 73°
Wed, Feb 02

45. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠BCD = (mAD + mAB
2
1 1
= (73 +132) = (205)
2 2
73° 73°
Wed, Feb 02

46. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠BCD = (mAD + mAB
2
1 1
= (73 +132) = (205) =102.5°
2 2
73° 73°
Wed, Feb 02

47. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
132° 82°
73° 73°
Wed, Feb 02

48. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠CDA = (mBC + mAB
2
73° 73°
Wed, Feb 02

49. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠CDA = (mBC + mAB
2
1
= (82 +132)
2
73° 73°
Wed, Feb 02

50. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠CDA = (mBC + mAB
2
1 1
= (82 +132) = (214)
2 2
73° 73°
Wed, Feb 02

51. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠CDA = (mBC + mAB
2
1 1
= (82 +132) = (214) =107°
2 2
73° 73°
Wed, Feb 02

52. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
132° 82°
73° 73°
Wed, Feb 02

53. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠DAB = (mBC + mCD
2
73° 73°
Wed, Feb 02

54. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠DAB = (mBC + mCD
2
1
= (82 + 73)
2
73° 73°
Wed, Feb 02

55. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠DAB = (mBC + mCD
2
1 1
= (82 + 73) = (155)
2 2
73° 73°
Wed, Feb 02

56. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
1  )
132° 82° m∠DAB = (mBC + mCD
2
1 1
= (82 + 73) = (155) = 77.5°
2 2
73° 73°
Wed, Feb 02

57. Example 1
 ≅ CD . Find the measures of the

In circle O, AD
angles of quadrilateral ABCD, when
 =132° and mBC = 82°.
mAB 
132° 82° m∠ABC = 73°
m∠BCD =102.5°
m∠CDA =107°
73° 73°
m∠DAB = 77.5°
Wed, Feb 02

58. Example 2
Identify the following for circle P.
a. Diameter b. Radius
c. Chord 
d. mLM


e. mLMK f. mLJ
g. m∠LKJ h. Central Angle
Wed, Feb 02

59. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK
c. Chord 
d. mLM


e. mLMK f. mLJ
g. m∠LKJ h. Central Angle
Wed, Feb 02

60. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM


e. mLMK f. mLJ
g. m∠LKJ h. Central Angle
Wed, Feb 02

61. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM
KL


e. mLMK f. mLJ
g. m∠LKJ h. Central Angle
Wed, Feb 02

62. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM
KL = 62° + 47°


e. mLMK f. mLJ
g. m∠LKJ h. Central Angle
Wed, Feb 02

63. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM
KL = 62° + 47° =109°


e. mLMK f. mLJ
g. m∠LKJ h. Central Angle
Wed, Feb 02

64. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM
KL = 62° + 47° =109°


e. mLMK f. mLJ
= 62° +180°
g. m∠LKJ h. Central Angle
Wed, Feb 02

65. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM
KL = 62° + 47° =109°


e. mLMK f. mLJ
= 62° +180° = 242°
g. m∠LKJ h. Central Angle
Wed, Feb 02

66. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM
KL = 62° + 47° =109°


e. mLMK f. mLJ
= 62° +180° = 242° = 62°
g. m∠LKJ h. Central Angle
Wed, Feb 02

67. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM
KL = 62° + 47° =109°


e. mLMK f. mLJ
= 62° +180° = 242° = 62°
g. m∠LKJ h. Central Angle
= 2 (62°)
1
Wed, Feb 02

68. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM
KL = 62° + 47° =109°


e. mLMK f. mLJ
= 62° +180° = 242° = 62°
g. m∠LKJ h. Central Angle
= 2 (62°) = 31°
1
Wed, Feb 02

69. Example 2
Identify the following for circle P.
a. Diameter b. Radius
JK KP
c. Chord 
d. mLM
KL = 62° + 47° =109°


e. mLMK f. mLJ
= 62° +180° = 242° = 62°
g. m∠LKJ h. Central Angle
= 2 (62°) = 31°
1
∠JPM
Wed, Feb 02

70. Problem Set
Wed, Feb 02

71. Problem Set
p. 228 #1-25 odd
“We are so accustomed to disguise ourselves to others
that in the end we become disguised to ourselves.”
- Francois de La Rochefoucauld
Wed, Feb 02