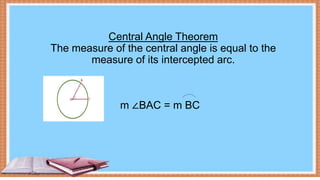
This document provides instruction on determining the relationship between arcs and central angles in a circle. It defines key terms like central angle, arc, and diameter. It explains the central angle theorem - that the measure of the central angle is equal to the measure of its intercepted arc. The document includes 4 examples problems where the user is asked to find the measure of angles and arcs in various circles given a central angle measurement. The objective is to help the user appreciate accumulated knowledge and solve for arc and angle measures in circles.

1. Good Afternoon 
Hi I’m Mary Rose B. Balongoy

2. 4PICS1 WORD

3. CIRCLE

4. ARC

5. Measurement of a
Central Angle and
Arcs of a Circle

6. Objectives:
a. Determine the relationship among arcs and central angle of the Circle.
b. Appreciate the value of accumulated knowledge as means of new
understanding.
c. Solve the measure of arcs, and central angles of a Circle.

7. Things to know and remember always:
A circle has 360 degrees.
A semicircle has 180 degrees.
Vertical Angles are equal.
Linear Pairs are Supplementary.

8. Central Angle Theorem
The measure of the central angle is equal to the
measure of its intercepted arc.
m ∠BAC = m BC

9. Example 1: In the diagram below, if the m ∠xyz is 68°, find the
measure of a.) minor arc b.) major arc
a. Measure of minor arc
m∠xyz = 68°
XZ = 68°
b. Measure of major arc
Major arc = 360°- m xz (minor arc)
= 360°- 68°
= 292°

10. Example:
EB is a diameter, ∠AQB = 96°. Find the
measure of the ff.
m AB = ?
= 96°
m ACB = ?
= 360°- 96°
= 264°
m AE = ?
= 180°- 96°
= 84°

11. Let’s work it out!
1. In the center x of the circle, find all the angles & arcs.
100°
AL = 100°
∠AXL = ?
LCA = ?
= 100°
= 360° - 100°
= 260°

12. 2. In the center C of the circle , find all the angles and arcs.
30°
EA = 30°
DB = ?
= 30°
ED = ?
= 150°
AB = ?
= 150°
= 150°
∠ACB = ?
∠ECA = 30°
∠DCB = 30
∠ECD = ?
= 180° - 30°
= 150°

13. 3. In the center C of the circle, find all the angles & arcs
142°
AD = 142°
∠ACD = ?
=142°
BA = ?
= 180° - 142°
= 38°
∠ACB = ?
= 38°
BD = ?
= 180°

14. 4. In the center C of the circle, find all the angles and arcs
85°
125°
AB = 85°
DL = 125°
∠DCL = ?
= 125°
BD = ?
= 180° - 125°
= 55°
AL = ?
= 95°
= 180° - 85°

15. Thank You for listening 