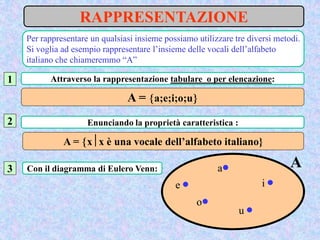
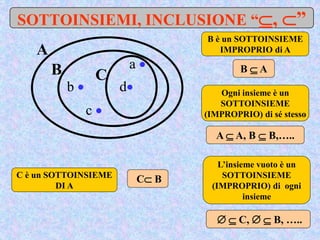
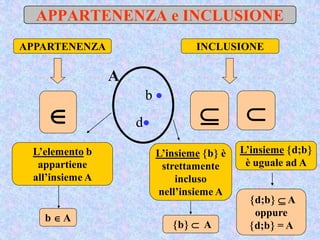
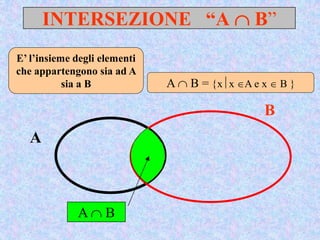
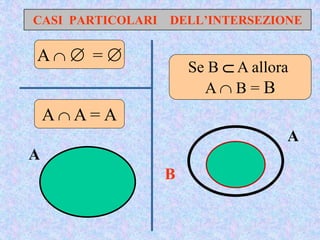
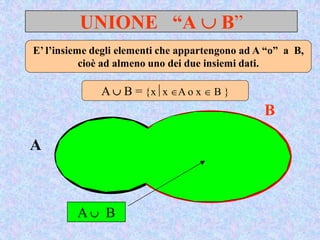
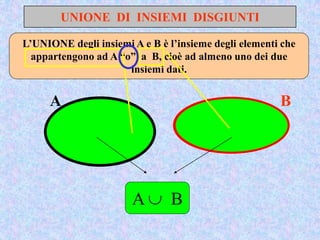
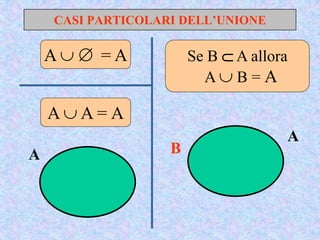
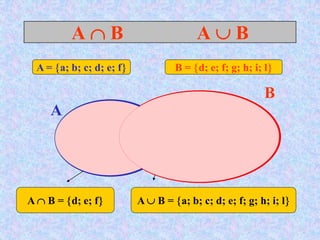
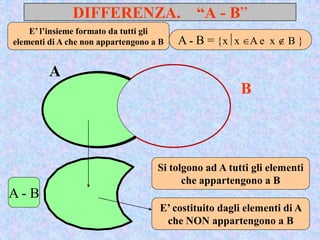
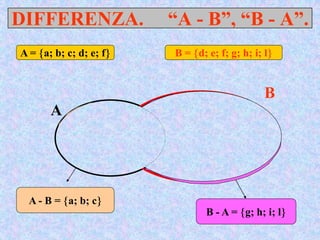
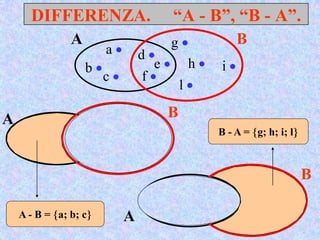
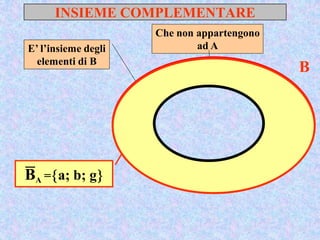
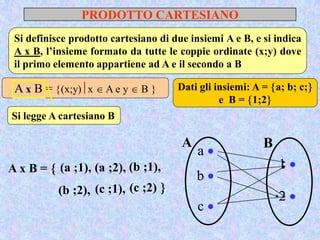
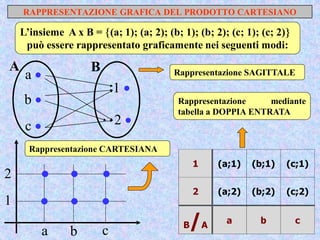
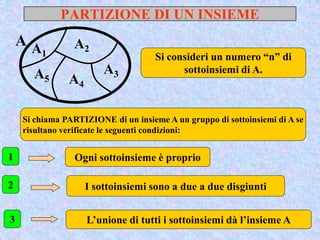
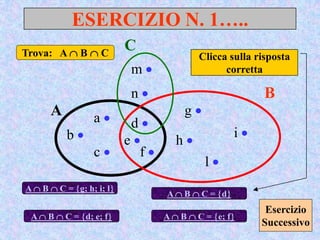
Il documento presenta un'introduzione al concetto di insieme in matematica, definendo raggruppamenti e simboli associati. Vengono esplorati vari tipi di insiemi e operazioni tra insiemi, come unione, intersezione e differenza. Inoltre, si discute il prodotto cartesiano e l'insieme delle parti, inclusa la regola per determinare il numero di sottoinsiemi.

1. GLI INSIEMI
Dispensa a cura del prof.
Vincenzo Lo Presti

2. CONCETTO DI INSIEME
In matematica si chiama insieme un raggruppamento di
cose, persone o entità che rispettano un determinato
criterio, mediante il quale si può stabilire con assoluta
certezza quali sono gli elementi che compongono l’insieme.
RAGGRUPPAMENTI CHE COSTITUISCONO INSIEMI
RAGGRUPPAMENTI CHE NON COSTITUISCONO INSIEMI
Le città italiane con più di 500.000 abitanti
Gli alunni della classe che pesano sino a 60 kg
I rettangoli che hanno la base di 10 cm
Le città italiane grandi
Gli alunni simpatici della classe
I rettangoli piccoli

3. SIMBOLOGIA DEGLI INSIEMI
Gli insiemi si indicano con le lettere maiuscole dell’alfabeto
italiano: A , B, C, D, E, ………
Gli elementi di un insieme si indicano con le lettere
minuscole dell’alfabeto italiano: a,b,c,d,e, ………
In matematica alcune lettere maiuscole sono riservate a
particolari insiemi numerici:
N Insieme dei numeri naturali
P Insieme dei numeri naturali pari
D Insieme dei numeri naturali dispari
Z Insieme dei numeri interi relativi
Q Insieme dei numeri razionali

4. SIMBOLOGIA DEGLI INSIEMI
Nello studio degli insiemi si utilizzano particolari simboli
c  B
 Simbolo di appartenenza
L’elemento c appartiene all’insieme B
4  N Il 4 appartiene all’insieme dei numeri naturali
 Simbolo di non appartenenza
-3  N Il -3 non appartiene all’insieme dei numeri
Naturali

5. TIPI DI INSIEMI
Gli insiemi possono essere:
Esempi:
Finiti – se hanno un numero ben preciso di elementi
Infiniti – se hanno infiniti elementi
L’insieme dei divisori di 12 è un insieme
finito in quanto ha un numero ben preciso
di elementi (sei ed esattamente 1,2,3,4,6,12)
L’insieme dei multipli di 6 è un insieme
infinito in quanto ha infiniti elementi
(6,12,18,24,30,36,42,48,54,60,66,72………)

6. INSIEME VUOTO
Un insieme si dice vuoto se non ha elementi
Esempi:
L’insieme vuoto si indica con  o con {}
L’insieme dei multipli di 4 che sono dispari
L’insieme dei quadrati con tre lati
L’insieme dei divisori di 13 che sono pari

7. RAPPRESENTAZIONE
Per rappresentare un qualsiasi insieme possiamo utilizzare tre diversi metodi.
Si voglia ad esempio rappresentare l’insieme delle vocali dell’alfabeto
italiano che chiameremmo “A”
Con il diagramma di Eulero Venn:
1
A
e  i 
a
o
2
Attraverso la rappresentazione tabulare o per elencazione:
3
Enunciando la proprietà caratteristica :
A = a;e;i;o;u
A = xx è una vocale dell’alfabeto italiano}
u 

8. SOTTOINSIEME
A
a 
b 
B
c 
e 
d
f 
A = a; b; c, d; e; f
B = b; d
Si dice che l’insieme B è sottoinsieme dell’insieme A se tutti
gli elementi di B appartengono anche ad A
B  A

9. SOTTOINSIEMI, INCLUSIONE “, ”
B è un SOTTOINSIEME
IMPROPRIO di A
C è un SOTTOINSIEME
DI A
Ogni insieme è un
SOTTOINSIEME
(IMPROPRIO) di sé stesso
A
a 
b 
B
c 
d
B  A
C B
A  A, B  B,…..
L’insieme vuoto è un
SOTTOINSIEME
(IMPROPRIO) di ogni
insieme
  C,   B, …..
C

10. APPARTENENZA e INCLUSIONE

INCLUSIONEAPPARTENENZA
b  A

b  A
L’elemento b
appartiene
all’insieme A
L’insieme b è
strettamente
incluso
nell’insieme A
b 
A
d 
L’insieme d;b
è uguale ad A
d;b  A
oppure
d;b = A

11. INTERSEZIONE “A  B”
A
B
A  B
E’ l’insieme degli elementi
che appartengono sia ad A
sia a B A  B = xx A e x  B 

12. INSIEMI DISGIUNTI
Due insiemi si dicono disgiunti se la loro
intersezione è vuota
Se A  B =  allora A e B si dicono DISGIUNTI
A B

13. CASI PARTICOLARI DELL’INTERSEZIONE
A  A = A
A   = 
Se B  A allora
A  B = B
A
B
A

14. UNIONE “A  B”
A
B
A  B
E’ l’insieme degli elementi che appartengono ad A “o” a B,
cioè ad almeno uno dei due insiemi dati.
A  B = xx A o x  B 

15. UNIONE DI INSIEMI DISGIUNTI
A B
L’UNIONE degli insiemi A e B è l’insieme degli elementi che
appartengono ad A “o” a B, cioè ad almeno uno dei due
insiemi dati.
A  B

16. CASI PARTICOLARI DELL’UNIONE
A  A = A
A   = A Se B  A allora
A  B = A
A
BA

17. A  B A  B
A
B
a  d 
c 
b  e 
f 
g 
h 
l 
i 
A = a; b; c; d; e; f B = d; e; f; g; h; i; l
A  B = d; e; f A  B = a; b; c; d; e; f; g; h; i; l

18. DIFFERENZA. “A - B”
A
B
A - B
Si tolgono ad A tutti gli elementi
che appartengono a B
E’ costituito dagli elementi di A
che NON appartengono a B
E’ l’insieme formato da tutti gli
elementi di A che non appartengono a B A - B = xx A e x  B 

19. DIFFERENZA. “A - B”, “B - A”.
A
B
a  d 
c 
b  e 
f 
g 
h 
l 
i 
A = a; b; c; d; e; f B = d; e; f; g; h; i; l
A - B = a; b; c
B - A = g; h; i; l

20. DIFFERENZA. “A - B”, “B - A”.
A B
a  d 
c 
b  e 
f 
g 
h 
l 
i 
A - B = a; b; c
B - A = g; h; i; l
A B
a  d 
c 
b  e 
f 
g 
h 
l 
i 
A
B
a  d 
c 
b  e 
f 
g 
h 
l 
i 

21. CASI PARTICOLARI DELLA DIFFERENZA
TRA INSIEMI
A - A = 
A -  = A
Se A  B =  allora A - B = A e B - A = B
Se B  A allora B - A = 

22. INSIEME COMPLEMENTARE
BA= A-B = xx A e x  B 
Dati due insiemi A e B con BA si chiama
complementare di B rispetto ad A la differenza A-B

23. INSIEME COMPLEMENTARE
A
B
a 
b 
c  e 
f 
g 
d 
BA =a; b; g
E’ l’insieme degli
elementi di B
Che non appartengono
ad A

24. PRODOTTO CARTESIANO
Si definisce prodotto cartesiano di due insiemi A e B, e si indica
A x B, l’insieme formato da tutte le coppie ordinate (x;y) dove
il primo elemento appartiene ad A e il secondo a B
A x B = (x;y)x  A e y  B 
Si legge A cartesiano B
Dati gli insiemi: A = a; b; c;
e B = 1;2
A
a 
b 
c 
B
1 
2 
A x B =  (a ;1), (a ;2), (b ;1),
(b ;2), (c ;1), (c ;2) 

25. RAPPRESENTAZIONE GRAFICA DEL PRODOTTO CARTESIANO
L’insieme A x B = (a; 1); (a; 2); (b; 1); (b; 2); (c; 1); (c; 2)
può essere rappresentato graficamente nei seguenti modi:
A
a 
b 
c 
B
1 
2 
Rappresentazione SAGITTALE
1 (a;1) (b;1) (c;1)
2 (a;2) (b;2) (c;2)
B/A a b c
Rappresentazione mediante
tabella a DOPPIA ENTRATA
a b c
1
2   
  
Rappresentazione CARTESIANA

26. OSSERVAZIONI SUL PRODOTTO CARTESIANO
La coppia (x;y) è diversa dalla coppia (y;x)
Gli elementi dell’insieme cartesiano sono coppie
A x A = A2
A x B  B x A
Se A e B hanno rispettivamente “n” e “m” elementi,
l’insieme A x B possiede “nxm” elementi.

27. INSIEME DELLE PARTI “P(A)”
A a 
c 
b 
A = a; b; c;
a; b; c
Dato un insieme A, l’insieme di
tutti i suoi SOTTOINSIEMI
propri e impropri, si definisce
insieme delle parti di A e si indica
con P(A)
I possibili SOTTOINSIEMI di A
sono:
 a b c a; b a; c b; c
P(A) =  ; a; b; c; a; b; a; c; b; c; a; b; c 
Gli elementi di P(A) sono
INSIEMI
Se A contiene n elementi,
P(A) ne contiene 2n
L’insieme delle parti di A è:

28. INSIEME DELLE PARTI “P(A)”
Gli elementi di P(A) sono INSIEMI ed esattamente tutti
i sottoinsiemi propri e i due sottoinsiemi impropri
(l’insieme stesso e l’insieme vuoto)
REGOLA PER DETERMINARE IL N. DI
ELEMENTI DELL’INSIEME DELLE PARTI
Se A contiene n elementi, P(A) ne contiene 2n
Esempi:
-Se n=3 (esempio precedente) 23=8
-Se n=5 (esempio precedente) 25=32
-Se n=1 (esempio precedente) 21=2

29. PARTIZIONE DI UN INSIEME
A
Si consideri un numero “n” di
sottoinsiemi di A.
Si chiama PARTIZIONE di un insieme A un gruppo di sottoinsiemi di A se
risultano verificate le seguenti condizioni:
A1
A2
A3
A4
A5
Ogni sottoinsieme è proprio
I sottoinsiemi sono a due a due disgiunti
L’unione di tutti i sottoinsiemi dà l’insieme A
1
2
3

30. ESERCIZIO N. 1…..
A
B
a  d 
c 
b  e 
f 
g 
h 
l 
i 
Trova: A  B  C
A  B  C = g; h; i; l
C
m 
n 
A  B  C = d; e; f
A  B  C = d
A  B  C = e; f
Clicca sulla risposta
corretta
Esercizio
Successivo