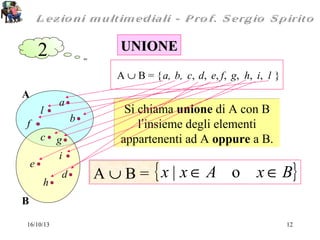
Il documento tratta il concetto di insieme, definendo i tipi di insiemi (finiti e infiniti) e come rappresentarli, inclusi esempi ed operazioni come unione, intersezione e differenza. Si discutono anche proprietà fondamentali delle operazioni sugli insiemi e l'idea di partizione degli insiemi. Infine, vengono forniti esercizi per applicare i concetti presentati.

1. Insiemi
16/10/13
1

2. Possiamo precisare il concetto di
insieme (termine primitivo)
come un aggregato di oggetti
determinati e distinti
Se gli elementi di un insieme sono elencabili
tutti, si dice finito, altrimenti infinito.
finito
infinito
16/10/13
2

3. Esempi:
1
2
L’insieme dei giorni di una settimana
Insieme finito
L’insieme dei numeri pari
Insieme infinito
3
16/10/13
L’insieme dei corpi freddi
Non è un insieme !!
3

4. Possiamo rappresentare un insieme nei seguenti tre modi:
1
Mediante una proposizione che indica la proprietà
caratteristica.
A = {x | x è un giorno della settimana}
B = {x | x è pari}
C = {x | x è un numero divisore di 20}
2
Elencando gli elementi dell’insieme.
A = {lunedì, martedì,….,domenica}
B = {0,2,4,6,8,10,12,...}
C = {1,2,4,5,10,20}
16/10/13
4

5. 3
Mediante diagramma di Eulero-Venn.
U
insieme
universo
3
B
1
8
0
11
4
6
2
5
10
12
7
9
B = {x | x è pari}
Scriviamo:
16/10/13
6∈ B
5∉ B
Simbolo di
appartenenza
Simbolo di non
appartenenza
5

6. Due insiemi si dicono uguali quando possiedono gli stessi elementi.
scriviamo:
A=B
Un insieme A si dice sottoinsieme di B quando ogni elemento di A
appartiene anche a B.
B
A
scriviamo:
A⊆ B
16/10/13
6

7. L’insieme vuoto è un insieme privo di elementi.
scriviamo:
∅
Esempi:
A = {x | x è positivo e minore di -1}
B = {x | x2 < 0}
C = {x | x è un mese di 32 giorni}
16/10/13
7

8. Dato un insieme A, l’insieme delle parti è l’insieme formato
da tutti i possibili sottoinsiemi di A.
scriviamo:
P(A)
Esempio:
A = { a, b, c}
P(A) = {A,∅,{a},{b},{c},{a,b},{a,c},{b,c}}
Esercizi: Trovare l’insieme delle parti dei seguenti insiemi
A = {1, c,3,4}
16/10/13
B = {1,4}
C = { a, c,4,7}
8

9. Si dimostra che se A è formato da n elementi
allora l’insieme delle parti è formato da 2n
elementi.
A
P(A)
a
b
c
3 elementi
16/10/13
A
∅
{b}
{a}
{c}
{a,c}
{b,c}
{a,b}
2 3 = 8 elementi
9

10. OPERAZIONI FRA INSIEMI
COMPLEMENTARE
1
B
m d
g
e
16/10/13
CB(A) = { b, d, e, g, m}
b
a
c
h
A
f
Se A⊆B si chiama
complementare di A rispetto a
B l’insieme degli elementi di B
che non appartengono ad A.
CB(A) = { x | x ∈ B e x ∉ A}
10

11. Domande:
B
16/10/13
CA(A) = ∅
CA(∅) = A
CB(CB(A)) =
A
A
11

12. UNIONE
2
A ∪ B = { a, b, c, d, e, f, g, h, i, l }
A
l
a
b
f
c
e
h
g
i
d
Si chiama unione di A con B
l’insieme degli elementi
appartenenti ad A oppure a B.
A ∪ B = {x | x ∈ A o
x ∈ B}
B
16/10/13
12

13. Domande:
B
Se A⊆B allora
A
A∪B= B
A ∪ CB(A) = B
A∪∅=A
A∪A=A
16/10/13
13

14. INTERSEZIONE
3
A ∩ B = { c, g }
A
l
a
b
f
c
e
h
g
i
d
Si chiama intersezione di A
con B l’insieme degli elementi
appartenenti ad A e a B.
A ∩ B = {x | x ∈ A e
x ∈ B}
B
16/10/13
14

15. Domande:
B
Se A⊆B allora
A
A∩B= A
A ∩ CB(A) =
∅
A∩∅=∅
A∩A=A
16/10/13
15

16. DIFFERENZA
4
A - B = { a, b, f, l }
A
l
a
b
f
c
e
h
g
i
d
Si chiama differenza fra A e B
l’insieme degli elementi
appartenenti ad A ma non a B.
A-B=
{x | x ∈ A
e
x ∉ B}
B
16/10/13
16

17. Domande:
B
Se A⊆B allora
A
A-B= ∅
A - CB(A) = A
B - A = CB(A)
A-∅= A
A-A= ∅
16/10/13
17

18. DIFFERENZA SIMMETRICA
5
A ∆ B = { a, b, d, e, f, h, i, l }
A
l
a
b
f
c
e
h
B
16/10/13
g
i
Si chiama differenza simmetrica
fra A e B l’insieme degli elementi
appartenenti ad A oppure a B ma
non alla loro intersezione.
d
A ∆ B = { x | x ∈ A o x ∈ B e x ∉ A ∩ B}
18

19. Domande:
B
Se A⊆B allora
A
A ∆ B = CB(A)
A ∆ CB(A) = B
B ∆ A = CB(A)
A∆∅= A
A∆A= ∅
16/10/13
19

20. PRODOTTO CARTESIANO
6
A × B = {(a,c), (a,e), (a,d), (b,c), (b,e), (b,d),(c,c), (c,e),(c,d)}
A
a
c
e
d
B
16/10/13
b
Si chiama prodotto cartesiano di
A e B l’insieme di tutte le coppie
del tipo (ai,bk), con ai ∈A e bk ∈B.
A× B
=
{ (ai , bk ) | ai ∈ A e bk ∈ B}
20

21. Rappresentazione saggittale del
prodotto cartesiano
Esempio:
1
A
a
2
B
3
b
4
5
A × B = { (a,1), (a,2),(a,3),(a,4),(a,5),(b,1),(b,2),
(b,3), (b,4), (b,5)}
16/10/13
21

22. Rappresentazione cartesiana del
prodotto cartesiano
Esempio:
A = { a, b}
B = {1,2,3,4,5}
B
5
4
3
2
1
a
A
b
A × B = { (a,1), (a,2),(a,3),(a,4),(a,5),(b,1),(b,2),
16/10/13
(b,3), (b,4), (b,5)}
22

23. 1
Proprietà commutativa
A∪ B = B ∪ A
2
A∩ B = B ∩ A
Proprietà associativa
( A ∪ B) ∪ C = A ∪ ( B ∪ C )
( A ∩ B) ∩ C = A ∩ ( B ∩ C )
16/10/13
23

24. 3
Proprietà di idempotenza
A∪ A = A
4
A∩ A = A
Proprietà distributiva
A ∪ ( B ∩ C ) = ( A ∪ B) ∩ ( A ∪ C )
Dell’intersezione
rispetto all’unione
16/10/13
Dell’unione
rispetto
all’intersezione
A ∩ ( B ∪ C ) = ( A ∩ B) ∪ ( A ∩ C )
24

25. Esercizi
Sia A={1,4,6}, B={2,3,4} e C={1,4,8}. Verificare che
1
A∪ B = B ∪ A
2
A ∪ ( B ∩ C ) = ( A ∪ B) ∩ ( A ∪ C )
3
A ∩ ( B ∪ C ) = ( A ∩ B) ∪ ( A ∩ C )
4
A ∩ ( B ∩ C ) = ( A ∩ B) ∩ C
16/10/13
25

26. Esercizi
Sia A= {1,4,6} , B = {4,5,6} e C= {1,2,3,4,5,6}. Verificare che
1
CC(A∪B) = CC(A) ∩ CC(B)
2
CC(A ∩ B) = CC(A) ∪ CC(B)
Leggi di De Morgan
16/10/13
26

27. Partizione di un insieme
A
1 A1 ∪ A2 ∪ A3 ∪ A4 = A
A2
A4
A1
A3
2 A1∩A2= ∅
A1∩A3= ∅
A1∩A4= ∅
……………...
A3∩A4= ∅
I sottoinsiemi A1, A2, A3, A4, costituiscono una partizione di A
16/10/13
27

28. Domande:
Dire se costituiscono una partizione di N, insieme
dei numeri naturali, i seguenti sottoinsiemi.
1
A = {x | x è un numero pari}
B = {x | x è un numero dispari}
SI
2
A = {x | x è un numero pari}
B = {x | x è multiplo di 3}
NO
3
A = {x | x è multiplo di 4}
B = {x | x è dispari}
NO
4
A = {x | x ≥100}
B = {x | x ≤100}
NO
16/10/13
28