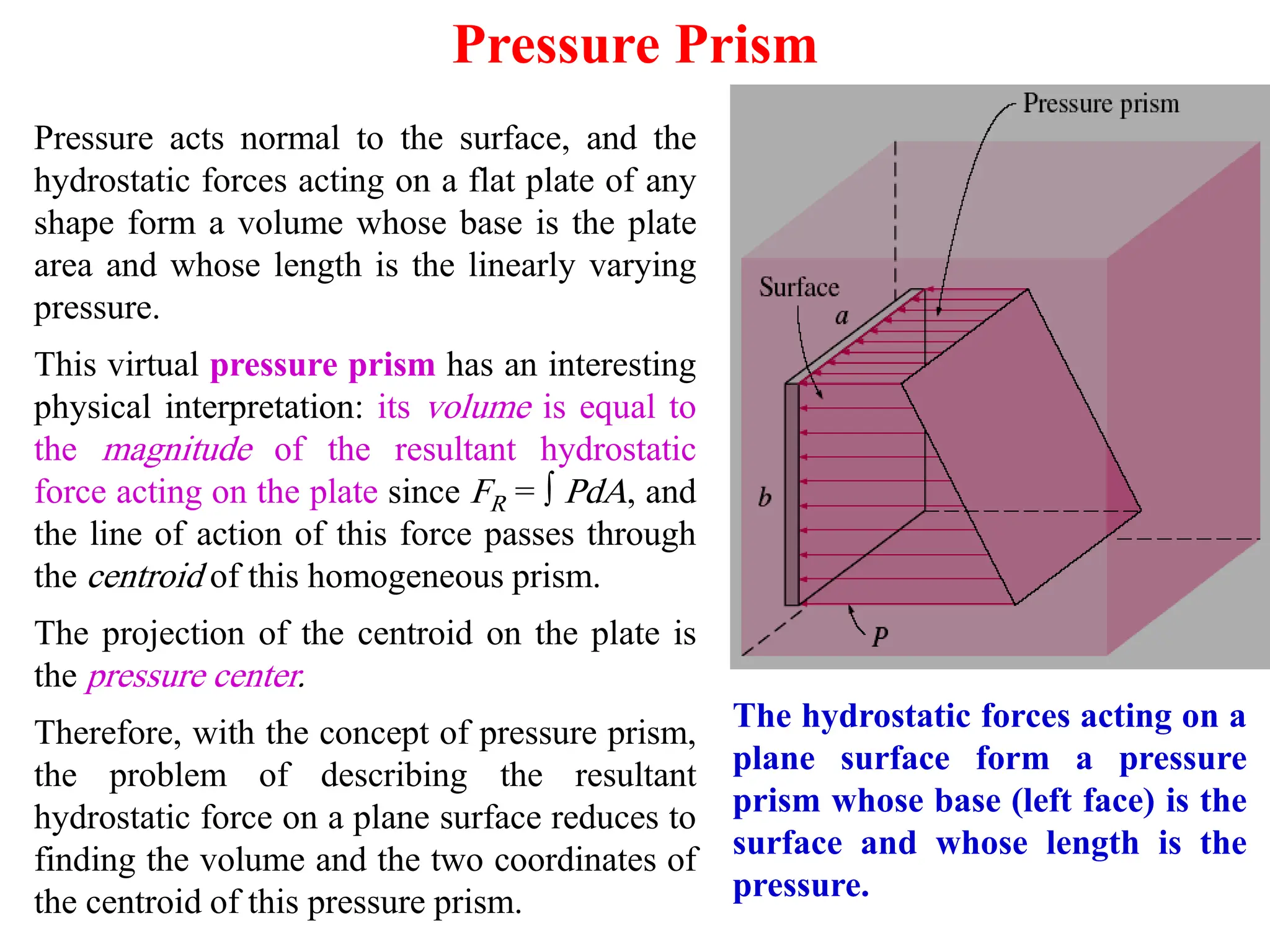
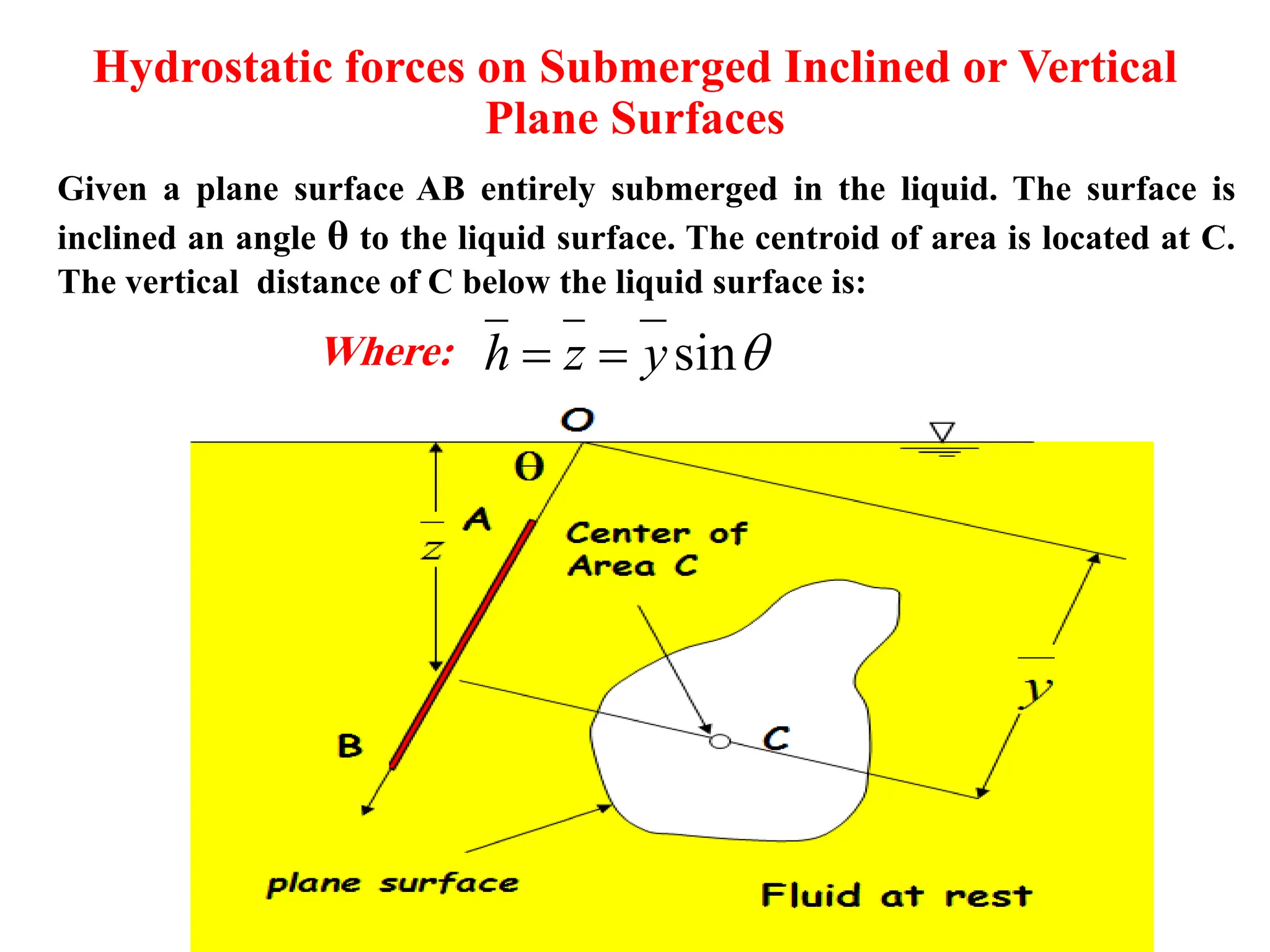
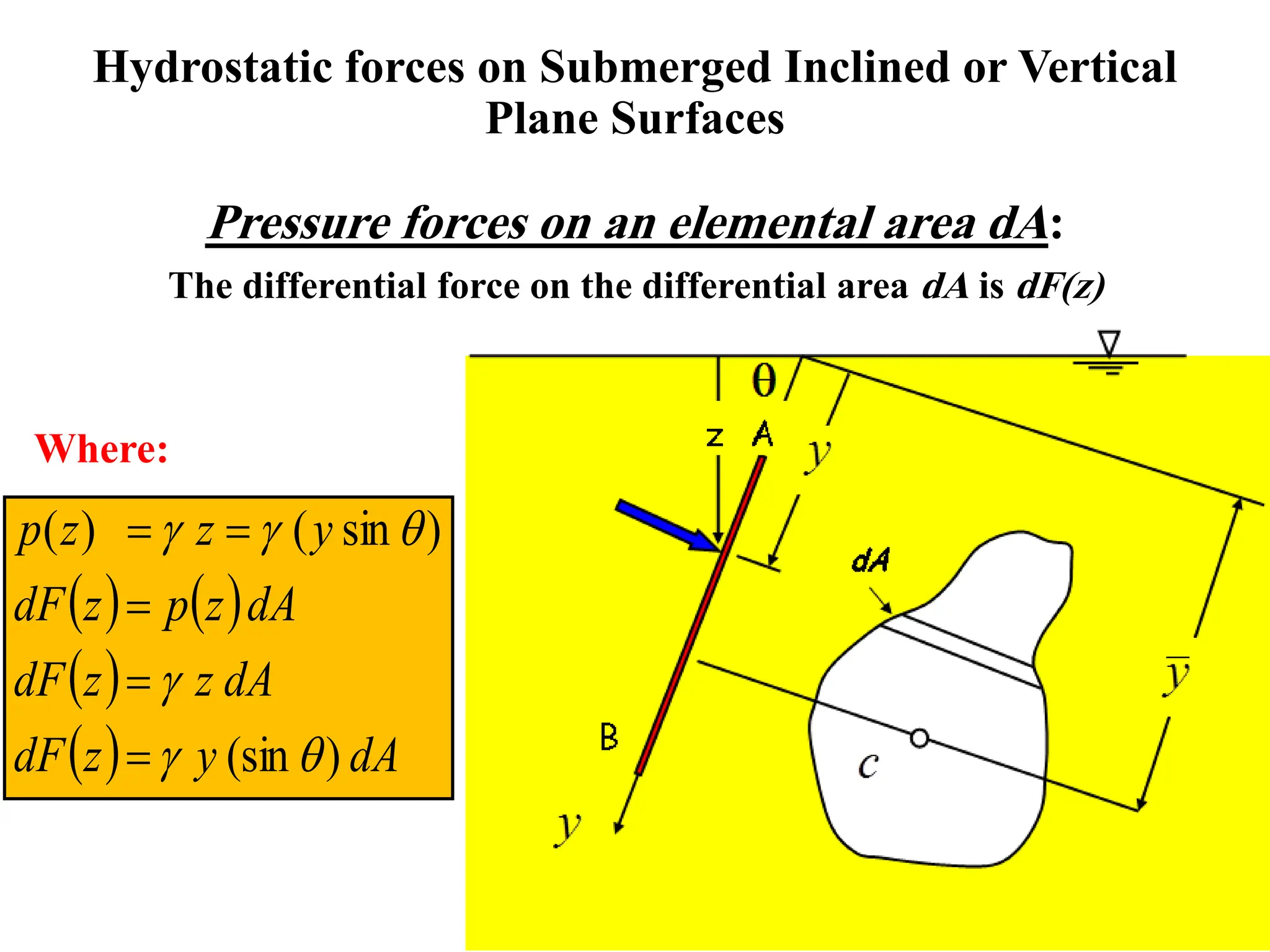
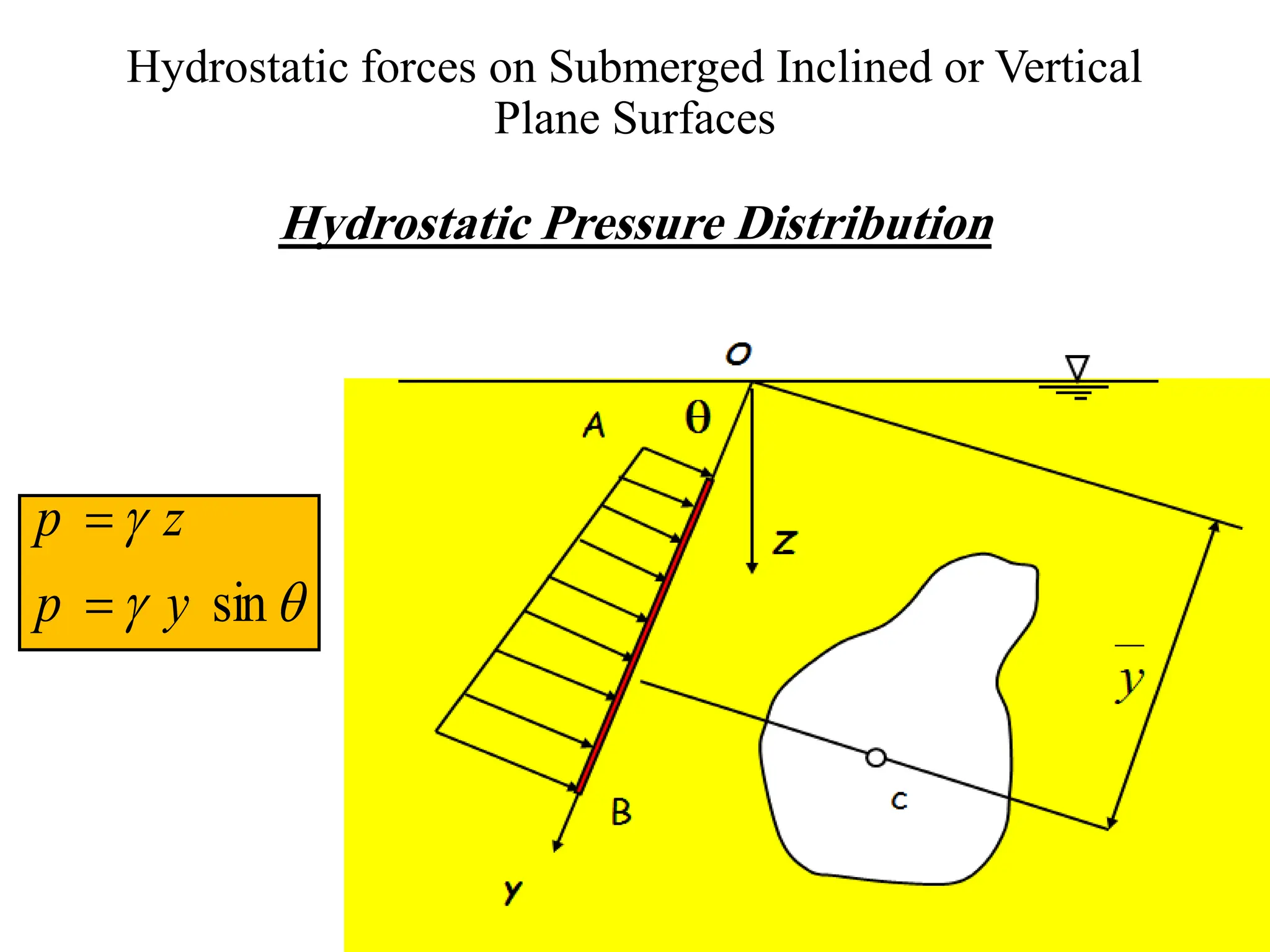
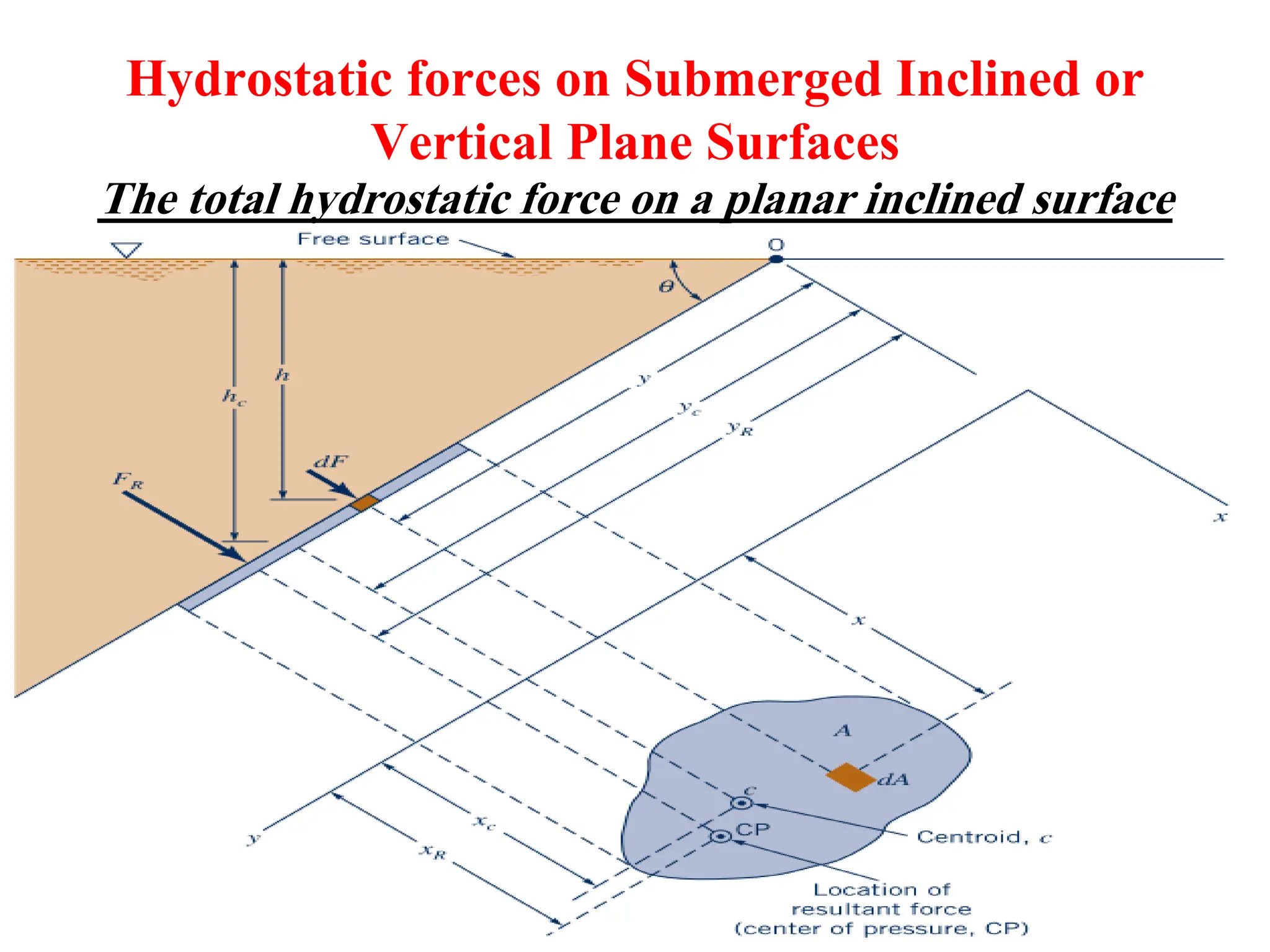
The document discusses hydrostatic forces on submerged plane surfaces. It provides analytical and graphical (prism) methods to calculate the total hydrostatic force and location of the center of pressure. As an example, it applies both methods to calculate the force on a submerged car door located 8 meters below the water surface. The analytical method yields a force of 101.24 kN and center of pressure at 0.144 meters above the bottom of the door. The prism method gives a force of 176.94 kN and center of pressure at 2.1 meters above the bottom.

1. Fluid Mechanics 1 –
Arab Academy for Science, Technology
and Maritime Transportation
Dr. Aly Hassan Elbatran
Associate Professor
a.elbatran@aast.edu
aly_marine@hotmail.com
Course Assistant Lecturer:
Eng. Islam mohamed

2. Lecture 4:
Hydrostatic Forces on Submerged
Plane Surfaces
Fluid Mechanics 1

3. Hydrostatic forces on submerged plane surfaces
Graphical Solution
(Prism Solution)
Analytical
Solution

4. Hydrostatic forces on submerged plane surfaces
Analytical
Solution

5. Hydrostatic forces on submerged plane surfaces
A plate is subjected to fluid pressure
distributed over its surface when
exposed to a liquid; such as a gate valve
in a dam, the wall of a liquid storage
tank, or the hull of a ship at rest.
On a plane surface, the hydrostatic
forces form a system of parallel forces,
and we often need to determine the
magnitude of the Resultant force and
its point of application, which is called
the center of pressure.
When analyzing hydrostatic forces on
submerged surfaces, the atmospheric
pressure can be subtracted for
simplicity when it acts on both sides of
the structure.

6. Hydrostatic forces on submerged plane surfaces
When analyzing hydrostatic forces on submerged surfaces, the atmospheric
pressure can be subtracted for simplicity when it acts on both sides of the
structure.
Effect of atmospheric pressure on the resultant force acting on a plane vertical wall.

7. General submerged plane

8. General submerged plane
The total area is made up of many elemental areas.
The force on each elemental area is always normal to the
surface but, in general, each force is of different magnitude
as the pressure usually varies.
We can find the total or Resultant Force, FR, on the plane
by summing up all of the forces on the small elements.
A
p
A
p
A
p
A
p
F n
n 






 ....
2
2
1
1
R


A
PdA
FR

9. Hydrostatic forces on Submerged Horizontal Plane
Surface
• For a horizontal plane submerged in a liquid, the pressure, p,
will be equal at all points of the surface.
• The pressure at the bottom of the container is uniform across the
entire area
pA
F 
R

10. Hydrostatic forces on Submerged Horizontal Plane
Surface
• For a horizontal plane submerged in a liquid, the pressure, p,
will be equal at all points of the surface.
• The pressure at the bottom of the tank is uniform across the
entire area
pA
F 
R
h A
FR 


11. 
sin
y
z
h 

Where:
Given a plane surface AB entirely submerged in the liquid. The surface is
inclined an angle θ to the liquid surface. The centroid of area is located at C.
The vertical distance of C below the liquid surface is:
Hydrostatic forces on Submerged Inclined or Vertical
Plane Surfaces

12. Pressure at a point at z
below the liquid surface
is:
p(z) = *z
(Gage pressure)
Or in terms of y
(distance along the plate)
pressure at point z is:
p(z) = *y*sin
The differential force
on the differential area
dA is dF(z)
Hydrostatic forces on Submerged Inclined or Vertical
Plane Surfaces
Pressure forces on an elemental area dA:

13. The differential force on the differential area dA is dF(z)
   
 
  dA
y
z
dF
dA
z
z
dF
dA
z
p
z
dF
y
z
z
p
)
(sin
)
sin
(
)
(











Hydrostatic forces on Submerged Inclined or Vertical
Plane Surfaces
Where:
Pressure forces on an elemental area dA:

14. Hydrostatic Pressure Distribution
Hydrostatic forces on Submerged Inclined or Vertical
Plane Surfaces



sin
y
p
z
p



15. The total force (FR) on the area will be obtained by integrating the
differential force over the entire area:
 dA
y
dF
FR sin

 
 

 and (sin ) are constants
 
   
    A
y
A
h
F
A
h
A
z
F
A
y
F
A
y
F
dA
y
F
c
c
R
R
R
R
R
sin
sin
sin
sin

















 
c
c
h
y






h
y
ydA
y
A
dA
A
Remark
The total hydrostatic force on a planar inclined surface
Hydrostatic forces on Submerged Inclined or
Vertical Plane Surfaces

16. The total hydrostatic force on a planar inclined surface
Hydrostatic forces on Submerged Inclined or
Vertical Plane Surfaces

17. yR of the resultant force can be determined by summation
of moments around the x axis. That is, the moment of the
resultant force must equal the moment of the distributed
pressure force, or
 dA
y
dF
FR sin

 
 

Recall that:
 dA
y
y
dF
y
y
F R
R 
 
 
 sin
So the moment is:
A
y
F c
R 
 sin

Recall that:

18. The integral in the numerator is the second moment of the area (moment of
inertia), “Ix”. Thus, we can write:
Using the parallel axis theorem:
where “Ixc”. is the second moment of the area with respect to an axis
through its centroid and parallel to the x axis. Thus:
So, from the above Equation, it is clear that the resultant force does not pass
through the centroid. but for nonhorizontal surfaces is always below it, since
(Ixc / ycA) > Zero
c
c
xc
c
c
xc
h
h
I
y
y
I




A
h
Or
A
y R
R

19. The centroid and the centroidal moments of inertia for
some common geometries

20. A heavy car plunges into a lake during an accident and lands at the bottom of the lake on its
wheels as shown in the Figure. The door is 1.2 m height and 1 m wide, and the top edge of
the door is 8 m below the free surface of the water. Using the analytical and prism method,
determine the hydrostatic force on the door and the location of the pressure center.
Example
m
8.61
)]
2
1.2
(
[8
1.2)
*
1
(
)]
2
1.2
(
[8
0.144
144
.
0
)
12
1.2
*
1
(
)
12
(
I
h
h
I
kN
101.24
kN
)
1
*
2
.
1
(
*
)]
2
1.2
(
[8
*
9.81
kN/m
9.81
and
4
3
3
xc
c
c
xc
3















R
R
R
R
w
c
w
R
h
m
ba
A
h
F
F
A
h
F 

Using the Analytical Method

21. Hydrostatic forces on submerged plane surfaces
Graphical Solution
(Prism Solution)

22. Pressure acts normal to the surface, and the
hydrostatic forces acting on a flat plate of any
shape form a volume whose base is the plate
area and whose length is the linearly varying
pressure.
This virtual pressure prism has an interesting
physical interpretation: its volume is equal to
the magnitude of the resultant hydrostatic
force acting on the plate since FR =  PdA, and
the line of action of this force passes through
the centroid of this homogeneous prism.
The projection of the centroid on the plate is
the pressure center.
Therefore, with the concept of pressure prism,
the problem of describing the resultant
hydrostatic force on a plane surface reduces to
finding the volume and the two coordinates of
the centroid of this pressure prism.
The hydrostatic forces acting on a
plane surface form a pressure
prism whose base (left face) is the
surface and whose length is the
pressure.
Pressure Prism

23. An alternate approach of determining the hydrostatic force is by
means of a pressure prism. Consider a vertical plane submerged in
a static fluid, as shown in the figure. The pressure increases
linearly with the depth. One can then easily construct a
corresponding three-dimensional diagram of the pressure
distribution, and such a volume is called a pressure prism. The
resultant force is the total volume of the pressure prism, that is:
FR = Volume = 1/2 (ρgh) (bh)
Pressure Prism

24. FR = Volume = 1/2 (ρgh) (bh)
The resultant force passes through the centroid of the pressure prism. For this
particular example, the centroid of a triangular element is located at a
distance of h/3 from its base and lies in the vertical symmetry axis.
As illustrated, this method is particularly convenient when the shape of the
pressure prism is a common geometry, in which the volume and centroid can
be readily obtained.
Pressure Prism

25. A heavy car plunges into a lake during an accident and lands at the bottom of the lake on its
wheels as shown in the Figure. The door is 1.2 m height and 1 m wide, and the top edge of
the door is 8 m below the free surface of the water. Using the analytical and prism method,
determine the hydrostatic force on the door and the location of the pressure center.
Using the Prism Method
 
 
m
61
.
8
)
59
.
0
2
.
1
8
(
that
So
;
59
.
0
*
24
.
01
1
)
3
2
.
1
(
*
063
.
7
)
2
2
.
1
(
*
176
.
94
*
)
3
2
.
1
(
*
)
2
2
.
1
(
*
0
kN
24
.
01
1
kN
063
.
7
)
1
*
2
.
1
(
*
2
)
8
2
.
1
8
(
*
9.81
kN
176
.
94
kN
)
1
*
2
.
1
(
*
8
*
9.81
2
and
,
2
1
2
1
2
1
1
2
2
1
1
























R
R
st
st
st
st
R
st
st
w
st
w
st
h
m
h
h
h
F
F
F
M
F
F
F
F
F
A
h
h
F
A
h
F 

Example