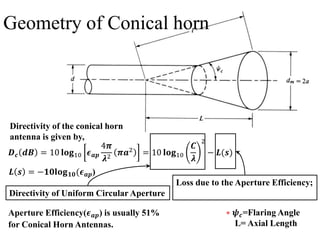
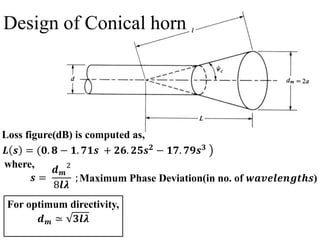
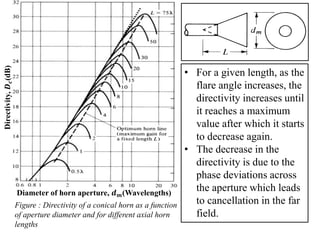
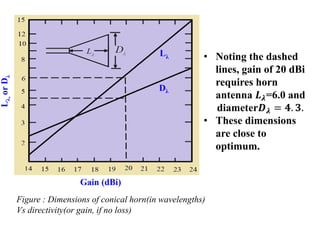
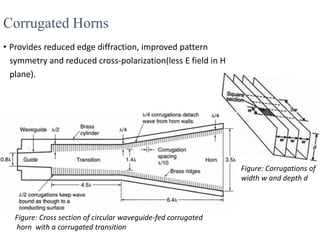
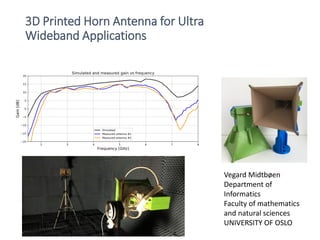
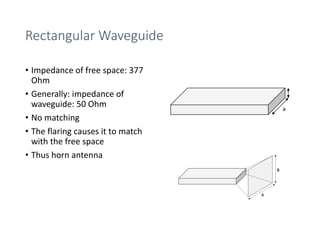
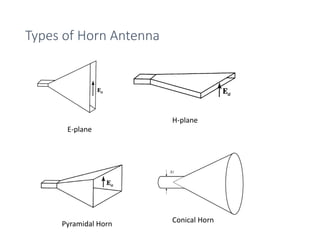
The document provides an overview of horn antennas, detailing various types including pyramidal, conical, and corrugated horns, along with their advantages and applications. It highlights key characteristics such as high gain, wide bandwidth, and low loss, making them suitable for numerous uses in communication and radar systems. Additionally, it outlines design considerations and specifications important for optimizing horn antenna performance.

1. Horn Antenna
Jiten Thapa
Safal Shrestha
Shulab Shrestha
2018.02.15
Department of Electrical and Electronics
Engineering
Kathmandu University

2. Overview
• Introduction
• Pyramidal Horn Antenna
• Conical Horn Antenna
• Corrugated Horns
• Sectoral Horn
• Advantages and Applications
Jiten Thapa
Safal Shrestha
Shulab Shrestha

3. Horn Antenna
• Horn antennas often have a directional radiation
pattern with a high antenna gain, which can
range up to 25 dB in some cases, with 10-20 dB
being typical.
• The bandwidth for practical horn antennas can
be on the order of 20:1 (for instance, operating
from 1 GHz-20 GHz), with a 10:1 bandwidth not
being uncommon
• Horn antennas have very little loss, so the
directivity of a horn is roughly equal to its gain

4. 3D Printed Horn Antenna for Ultra
Wideband Applications
Vegard Midtbøen
Department of
Informatics
Faculty of mathematics
and natural sciences
UNIVERSITY OF OSLO

5. Rectangular Waveguide
• Impedance of free space: 377
Ohm
• Generally: impedance of
waveguide: 50 Ohm
• No matching
• The flaring causes it to match
with the free space
• Thus horn antenna
a

6. Rectangular Waveguide
• Impedance of free space: 377
Ohm
• Generally: impedance of
waveguide: 50 Ohm
• No matching
• The flaring causes it to match
with the free space
• Thus horn antenna
a

7. Types of Horn Antenna
E-plane
H-plane
Pyramidal Horn Conical Horn

8. Pyramidal Horn Antenna
• has flaring on both sides.
• If flaring is done on both the E & H walls of a rectangular waveguide,
then pyramidal horn antenna is produced.
• this antenna has the shape of a truncated pyramid.
• probably the most popular antenna in the microwave frequency
ranges (from ≈1 GHz up to ≈18 GHz)

9. Radiation Pattern
This antenna is simulated
using a commercial solver,
FEKO (which runs method of
moments). The radiation
pattern at 2 GHz is shown
right side
a=3.69 inches, b=1.64 inches
A=30 inches, and B=23.8
inches

10. PYRAMIDAL HORN
TOP VIEW SIDE VIEW
A
𝜌ℎ
𝜓ℎ 𝜌2
𝑝ℎ
𝑎1
a A
𝜌 𝑒
𝜓ℎ 𝜌1
𝑝 𝑒
𝑏1
b

11. Pyramidal Horn Antenna
𝐸𝑦′
𝑥′
, 𝑦′
= 𝐸0 𝐶𝑜𝑠
𝜋
𝑎1
𝑥′ 𝑒
−𝑗 𝑘
𝑥′2
2𝜌2
+
𝑦′2
2𝜌1
𝑝 𝑒 = (𝑏1 − 𝑏)
𝜌 𝑒
𝑏1
2
−
1
4
1
2
𝑝ℎ = (𝑎1 − 𝑎)
𝜌ℎ
𝑎1
2
−
1
4
1
2
For Physical Realization 𝑝 𝑒 = 𝑝ℎ

12. 𝐺0 =
4𝜋
𝜆2
𝑎1 𝑏1 ∗ 0.5
𝐷 𝑝 =
𝜋𝜆2
32𝑎𝑏
𝐷 𝐸 𝐷 𝐻
𝑎1 = 3𝜆𝜌2 = 3𝜆𝜌ℎ
𝑏1 = 2𝜆𝜌1 = 3𝜆𝜌 𝑒
𝑝 𝑒 = (𝑏1 − 𝑏)
𝜌 𝑒
𝑏1
2
−
1
4
1
2
𝑝ℎ = (𝑎1 − 𝑎)
𝜌ℎ
𝑎1
2
−
1
4
1
2
Directivity of
Pyramidal Horn
Antenna can be
obtained using
Directivity
curves for E-and
H-Planes
Sectoral Horn
antenna
Alternatively

13. 2𝜒 −
𝑏
𝜆
2
2𝜒 − 1 =
𝐺0
2𝜋
3
2𝜋
1
𝜒
−
𝑎
𝜆
2
𝐺0
2
6𝜋3
1
𝜒
− 1
Combining all the equations

14. Design Procedure
2𝜒 −
𝑏
𝜆
2
2𝜒 − 1 =
𝐺0
2𝜋
3
2𝜋
1
𝜒
−
𝑎
𝜆
2
𝐺0
2
6𝜋3
1
𝜒
− 1



1
8
2
3
0G
h 


22
)( 0
1
G
trialx 
 e



2
3
2
33 0
21
G
a h 
 222 11  eb
1.
2.
3.
4.

15. X-Band (8.2-12.4 GHz), f=11 GHz Horn
Gain=22.6 dB
a=2.286 cm
b=1.016 cm
Find: Dimensions of Pyramidal Horn
0100 log106.22)( GdBG  97.18110 26.2
0 G
7273.2
1011
1030
9
9

x
x

 3725.0
7273.2
016.1
b 8382.0
7273.2
286.2
a
cm
NUMERICAL
At
f=11
GHz

16. Initial value of χ
5539.11
22
97.181
22
0
1 


G
316.301157.11  e
753.320094.12
1
8
2
3
0
 


G
h
2𝜒 −
𝑏
𝜆
2
2𝜒 − 1 =
𝐺0
2𝜋
3
2𝜋
1
𝜒
−
𝑎
𝜆
2
𝐺0
2
6𝜋3
1
𝜒
− 1Put this value in eqn
After few more tries χ=11.1157
cm
cm
NUMERICAL

17. 370.16002.6
2
3
2
33 0
21  



G
a h
859.12715.4222 11   eb
286.27005.10
4
1
)(
2
1
2
1
21 














 

b
bbp e
e
286.27005.10
4
1
)(
2
1
2
1
21 














 

a
aap h
h
cm
cm
NUMERICAL
cm
cm

18. Final Design
X-Band (8.2-12.4 GHz), f=11 GHz Horn
Gain=22.6 dB
286.27 he pp
85.12
370.16
1
1


b
a cm
cm
a=2.286 cm
b=1.016
waveguide
SIZE OF HORN
NUMERICAL

19. With a blink
of an eye
If you have
this graph
For Gain:
22.6 dBi

20. PHYSICAL SPECIFICATIONS
Width 36.4 mm (1.43 in)
Depth 58.8 mm (2.32 in)
Height 25.9 mm (1.02 in)
Weight 125 g (0.28 lb)
Material gold–plated brass
ELECTRICAL SPECIFICATIONS
Polarization linear
Frequency Range (33) 38 – 50 GHz
VSWR max. < 1.3:1
Impedance 50 Ω
Connector 2.4mmfemale
Gain 19 - 21 dB
http://www.rfspin.cz/en/antennas
/pyramidal-horn-antennas/ha50

21. G= 10 ln
4𝜋𝑎𝑏
𝜆2 + 𝜂 𝑒 + 𝜂ℎ [𝑑𝐵]
𝜂 𝑒, 𝜂ℎ = 𝑎𝑝𝑒𝑟𝑡𝑢𝑟𝑒 𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑐𝑦
le
lh
a
b

22. Optimization of Horn Antenna
𝐺 𝑜𝑝𝑡 = 10 ln
𝑎𝑏
𝜆2
+ 8.08 [𝑑𝐵]

23. Conical Horn Antennas
• Conical in shape with circular cross-section
• Fed is often a circular waveguide.

24. Geometry of Conical horn
𝑫 𝒄 𝒅𝑩 = 10 𝐥𝐨𝐠10 𝝐 𝒂𝒑
4𝝅
𝝀2
𝝅𝒂2
= 10 𝐥𝐨𝐠10
𝑪
𝝀
2
− 𝑳(𝒔)
𝑳 𝒔 = −𝟏𝟎𝐥𝐨𝐠 𝟏𝟎(𝝐 𝒂𝒑)
Directivity of Uniform Circular Aperture
Loss due to the Aperture Efficiency;
Directivity of the conical horn
antenna is given by,
Aperture Efficiency(𝝐 𝒂𝒑) is usually 51%
for Conical Horn Antennas.
∗ 𝝍 𝒄=Flaring Angle
L= Axial Length

25. Design of Conical horn
For optimum directivity,
𝒅 𝒎 ≃ 𝟑𝒍𝝀
𝒔 =
𝒅 𝒎
2
8𝒍𝝀
;
𝑳 𝒔 = (𝟎. 𝟖 − 𝟏. 𝟕𝟏𝒔 + 𝟐𝟔. 𝟐𝟓𝒔 𝟐 − 𝟏𝟕. 𝟕𝟗𝒔 𝟑
Loss figure(dB) is computed as,
where,
Maximum Phase Deviation(in no. of 𝒘𝒂𝒗𝒆𝒍𝒆𝒏𝒈𝒕𝒉𝒔)

26. • For a given length, as the
flare angle increases, the
directivity increases until
it reaches a maximum
value after which it starts
to decrease again.
• The decrease in the
directivity is due to the
phase deviations across
the aperture which leads
to cancellation in the far
field.
Directivity,𝑫𝒄(dB)
Diameter of horn aperture, 𝒅 𝒎(Wavelengths)
Figure : Directivity of a conical horn as a function
of aperture diameter and for different axial horn
lengths

27. Figure : Dimensions of conical horn(in wavelengths)
Vs directivity(or gain, if no loss)
• Noting the dashed
lines, gain of 20 dBi
requires horn
antenna 𝑳 𝝀=6.0 and
diameter𝑫 𝝀 = 𝟒. 𝟑.
• These dimensions
are close to
optimum.

28. Radiation Pattern of Conical Horn
Antenna should be designed in such a way that the
wave’s direction from antenna is perpendicular to
horn aperture.

29. Corrugated Horns
• Provides reduced edge diffraction, improved pattern
symmetry and reduced cross-polarization(less E field in H
plane).
Figure: Cross section of circular waveguide-fed corrugated
horn with a corrugated transition
Figure: Corrugations of
width w and depth d

30. Corrugated Horns
• Efficiencies of the order of 75–80% can be
obtained with improved feed systems utilizing
corrugated horns.
• Corrugations with depth λ/2 acts as a conducting
surface while that with λ/4 depth in horn antenna
present a high impedance.

31. Sectoral Horn Antenna
Shulab Shrestha

32. Sectoral Horn Antenna
• A pyramidal horn with only one pair of sides flared and the other pair
parallel.
• It produces a fan-shaped beam, which is narrow in the plane of the
flared sides, but wide in the plane of the narrow sides.
• These types are often used as feed horns for wide search radar
antennas.

33. Types of Sectoral Horn Antenna
• E-plane horn antenna : This form of antenna is one that is flared in
the direction of the electric or E-field in the waveguide.
• H-plane horn antenna : This form of antenna is one that is flared in
the direction of the electric or H-field in the waveguide.

34. Advantages of Horn Antenna
• They can operate over wide ranges of frequencies.
• Very wide bandwidth, for example allowing it to operate from 1GHz
to 20GHz, 20:1.
• High Directivity.
• High gain.
• Support for wide applications.

35. Applications
• They are used as feeders (called feed horn) for larger antenna
structures such as parabolic antennas, as directive antennas for such
devices as radar guns, automatic doors openers, microwave
radiometer.
• A common element of phase array.
• Satellite and microwave communications.
• Used in the calibration, other high gain antenna.
• Used for making electromagnetic interference measurement.

36. References
• Antenna-theory.com
• Antennas and Wave Propagation, John D Kraus
• Satellite Communication, Lecture Slide, Ippei Kashiwagi
• www.rfspin.cz
• 3D Printed Horn Antenna for Ultra Wideband Applications, Vegard
Midtbøen
• Horn Antennas, Prof. Girish Kumar